基于Kriging代理模型的主轴箱稳健设计
2011-08-01陈永亮王汉涛顾佩华
陈永亮,刘 双,王汉涛,张 健,顾佩华
(1. 天津大学机械工程学院,天津 300072 2. 汕头大学工学院,汕头 510063)
机械机构的材料特性、结构参数以及所受载荷等的不确定性将导致其性能产生波动.为进一步提高机械结构的性能,需要引入稳健设计方法[1-3],达到既提高产品质量,又可降低成本的目的.
分析性稳健设计方法[4-6]是一种分析研究系统稳健性的方法,设计者可以根据产品的功能需求,建立不确定因素、设计参数以及结构特性与产品功能特性之间的映射关系,对系统敏感性进行分析,并且按照所提供的优化模型对系统进行稳健优化设计,从而得到稳健的产品设计方案.不仅如此,该理论能够建立相应的稳健灵敏性矩阵,这就使系统敏感性问题得以量化解决.
分析性稳健设计需要有明确的公式来反映功能需求及性能约束与设计变量之间的关系,对于简单问题可以直接得到解析公式,而复杂工程问题难以直接建立公式,则须通过“采样-试验-拟合”的方式来构造代理模型(也称元模型,近似模型).代理模型技术主要包含2方面的内容:①构造模型的样本点如何选取,这与代理模型的取样策略有关,属于试验设计的范围;②数据拟合与预测模型的建模,这是代理模型的主体,在数学上属于近似方法的范围.所有代理模型的建模都是围绕这2方面内容展开的,如响应曲面模型、径向基函数、Kriging模型和非参数双响应曲面法[7]等.
Kriging模型是一种估计方差最小的无偏估计模型,它通过相关函数的作用,具有局部估计的特点,可对区域化变量求最优、线性、无偏内插估计值,具有平滑效应及估计方差最小的统计特征.由于Kriging建模技术可以提供最佳的无偏差预测法,所以它作为近似确定计算机模型越来越受到欢迎.同时,基于Matlab的Kriging工具箱——DACE[8]的开发,为使用Kriging提供极大的方便.目前Kriging模型已经成为多学科设计优化中比较有代表性的一种代理模型近似方法. Kriging方法已被广泛用于许多近似模拟确定的计算机模型响应.谢延敏[9]在其博士论文中将Kriging模型和灰色关联分析应用于板料成形工艺稳健优化设计中;瓦西姆拉扎和光永金[10]用Kriging建模技术对线装燃料组件进行形状优化;黄风立等[11]将关联度和 Kriging代理模型应用于注塑成型的稳健设计中;高月华等[12]将双重Kriging 代理模型和多点加点准则结合进行稳健优化设计.
本文主要研究基于Kriging代理模型的分析性稳健设计方法,采用 Kriging代理模型法,开发基于DACE的符号计算功能,拟合动静刚度对各个设计变量的关系公式,建立方差稳健设计模型,并进行稳健性分析和优化,最后以数控圆柱内齿轮铣齿机主轴箱稳健设计为例进行验证.
1 Kriging代理模型与分析性稳健设计集成过程
如图1所示,利用代理模型进行稳健设计首先需要根据设计要求确定设计参数(各个结构尺寸等)及响应变量(变形、质量、频率等),建立参数化有限元模型.然后设计正交试验,得到各组试验对应的响应值后,便可建立 Kriging代理模型.利用代理模型求解各个响应变量的均值及方差,构建稳健性分析模型,这是稳健设计的关键.进而可以进行稳健优化获取优化解.当然,最终的优化解需要多次重复以上过程并对比结果才能得到.由于最终的解是利用拟合公式(代理模型)优化而来,并不一定能很好地反映实际模型在最优值处的情况,所以最后需要对优化解进行有限元验证,验证结果与优化结果相差较大时,须重新设计正交试验,或提高拟合公式的精度.
由于所建立的代理模型公式表达式的复杂性,利用 DACE工具箱和自行开发的分析性稳健设计工具箱,已实现上述过程的有机集成.

图1 基于Kriging模型的分析性稳健设计流程Fig.1 Flow chart of analytical robust design based on Kriging model
1.1 参数化有限元模型及正交试验
设 X为设计参数向量,X =[x1, x2,… ,xn];设Y为响应参数向量,Y =[y1, y2,… , yn]T.
根据正交试验原理,采用均匀采样的方式将所有设计参数分为若干水平,组合得到若干组试验,然后利用建立好的参数化模型进行有限元计算,得出每组试验对应的响应值.
设正交试验组合中总样本个数为 n, Xi、 Yi(i=1 ,2,…,n )分别表示第 i个样本的变量参数和响应值,则 Xs=[X1, X2, … ,Xn]T、Ys=[Y1, Y2,… ,Yn]T表
示全体样本的变量集合和响应值集合.
1.2 Kriging代理模型
当系统的响应参数只有 1个时,此处假设为 y,Kriging模型的表达式为
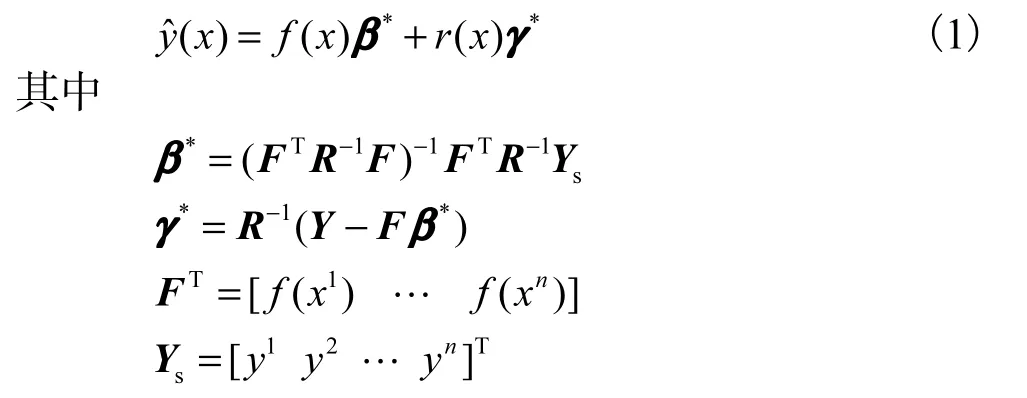
式中:()ˆy x为要估计的未知函数;f(x)是已知的回归模型,本文采用二阶多项式函数;γ∗为一常数矩阵;β∗ 为回归模型多项式的系数.r(x)是通过量化采样点与高斯相关点的相关性创建的一个局部偏差;R是一个相关矩阵.
在 Matlab环境下通过定义符号变量,利用DACE工具箱对正交试验得到的试验数据进行处理,即可得到基于Kriging代理模型的响应参数和设计参数之间的拟合公式.
1.3 模型精度检验
精度检验是判断代理模型是否可信的关键,若精度满足要求,则该代理模型可以替代原优化模型中的精确分析模型;否则需要修改试验设计,更换近似技术,或者调整设计变量、设计范围等,重新构建代理模型.
检验代理模型精度时,可以取设计空间中除建立代理模型用到的样本点以外的其他一些样本点作为检验点,计算相对均方根误差R,根据R值的大小判断模型精度是否满足要求,R值越小,模型精度越高.
R的计算公式为
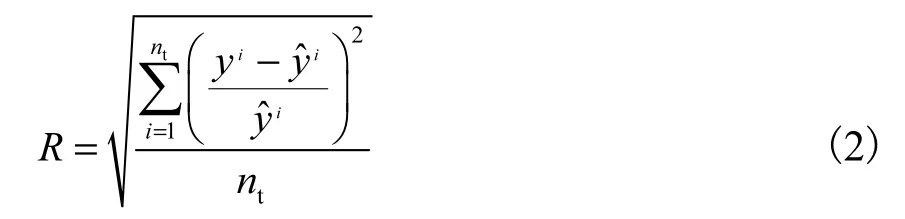
式中:yi和yˆi分别为设计空间上各点的真值和响应面的估计值;nt为设计空间上检验点的数量.
1.4 考虑噪声变量的分析性稳健设计模型
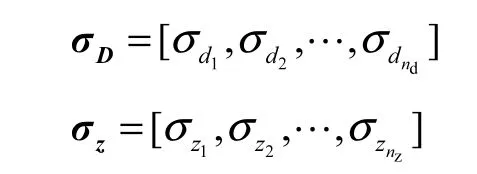
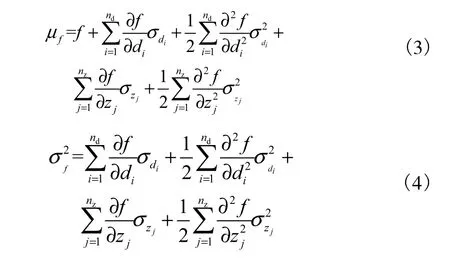
将代理模型代入式(3)和(4),即可得到待设计模型功能需求的均值、方差及灵敏度,进而可以建立方差稳健设计模型为

式中:0f为功能需求 f的期望值;[g]为约束函数g的允许值;,lbid 、,ubid 分别表示第 i个设计变量的下限和上限.
稳健设计模型建好以后,采用优化算法对稳健设计模型进行优化求解.
1.5 稳健优化结果的有限元验证
用所得的稳健优化解作为设计参数值代入参数化模型重建,并进行有限元分析,将所得响应值与稳健优化所得值进行校对,有限元验证值与优化结果相差较大时,需重新设计正交试验,或提高拟合公式的精度,进而重新进行稳健设计.
2 主轴箱稳健设计实例
2.1 主轴箱的参数化有限元分析模型
高速铣齿机床主轴箱[1]是机床的关键部件,孔系紧凑,结构较复杂,受载不均匀.主轴箱体结构的静、动态特性及其参数优化等是机床设计的关键,它们直接影响整机的静刚度和动态特性.主轴箱结构及与工件的位置关系如图2所示.图2中L1为主轴箱横梁长度,L2为主轴箱竖梁长度,DW为齿轮毛坯内孔直径,HW为毛坯壁厚,BW为毛坯厚度.
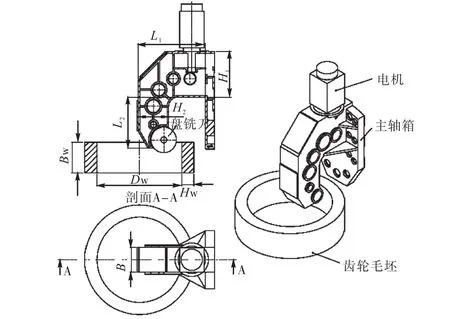
图2 主轴箱外形尺寸及与工件的几何关系Fig.2 Dimensions of the headstock and its geometry relation with the workpiece
图3(a)为横梁截面,外壁和内壁厚度分别为b0、b1,两内壁之间间隙为 d1,截面宽度为 B,高度为 H1.图 3(b)为竖梁截面,外壁和内壁厚度分别为 b0、b2,两内壁之间间隙为d2,截面宽度为B,高度为H2.

图3 梁截面Fig.3 Beam sections
根据以上对主轴箱结构的分析,选取横梁高度、竖梁高度、外壁厚度、内壁厚度以及梁宽度为设计变量,如表 1所示.弹性模型 E为噪声变量,E=2.0×105,MPa,其标准差为 6,000.设计变量和噪声变量统一定为设计参数.X方向变形δx(μm)、Z方向变形δz(μm)、质量 m(kg)以及一阶固有频率 f0(Hz)为响应参数.
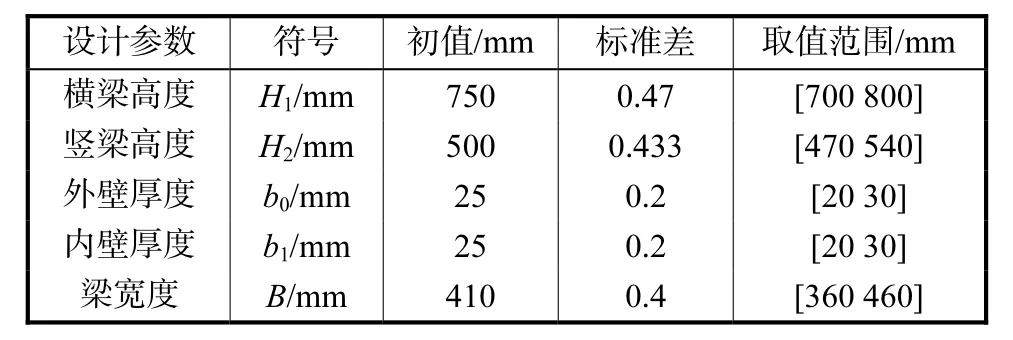
表1 设计变量Tab.1 Design variables
2.2 正交试验
将各个变量参数在规定范围内划分为4个水平,如表2所示,并组合为4水平正交表L32(49)可得32组试验.
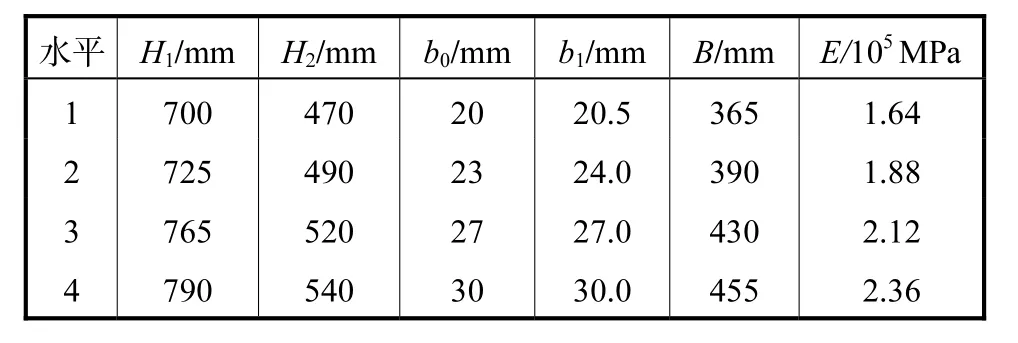
表2 变量参数的4个水平划分Tab.2 Four-level variable demacration
每次取4水平正交表L32(49)中的一组变量参数,在ansys中建立主轴箱的有限元模型,施加边界条件和载荷,经有限元计算后可得到32组试验结果.
综上所述,相较于常规骨科护理模式,在骨科护理中应用临床护理路径效果极好,有利于缩短患者的住院时间,提高患者的健康知识掌握程度,降低患者的并发症发生几率,患者的护理满意度更高。所以临床护理路径可以在骨科临床护理上推广应用。
2.3 主轴箱代理模型建立及其精度检验
以 32组试验数据为样本点,利用自行开发的Robust Design 稳健设计软件中的 DACE模块构建Kriging代理模型.选用二次回归函数 regpoly2,高斯校正函数corrgauss(如图4所示)进行计算,即可构建δx、δz、m 及 f1的拟合公式.

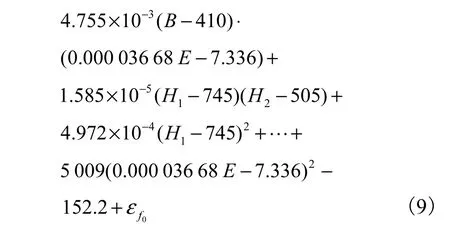
式中ε表示校正项.
图4 稳健设计软件的DACE模块Fig.4 DACE module of the robust design software
另选取 4水平表(表 2)中各个元素相邻元素之间的数建立3水平表,如表3所示.
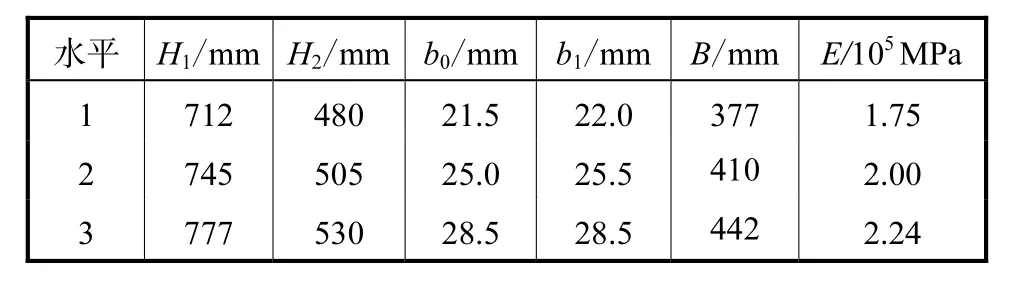
表3 变量参数的3个水平划分Tab.3 Three-level variable demacration
建立L18(37)正交表,将各组试验值代入式(6)~式(9),并重新进行有限元分析,对比二者结果.根据式(2)求得相对均方根误差为
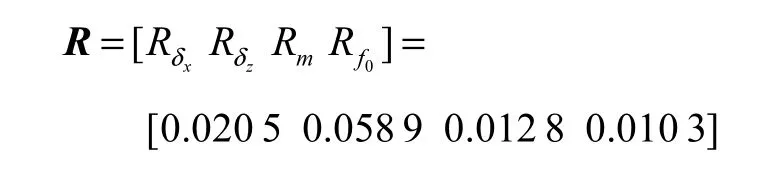
可见,各个响应变量的代理模型相对均方根误差最大为5.89%,满足工程问题的精度要求.
2.4 多目标稳健优化设计模型的建立
根据设计要求,设定主轴箱的x方向和z方向变形为功能需求,以功能需求的方差为目标函数,功能需求期望值为等式约束,主轴箱的质量固有频率和结构布局为性能约束,建立多目标稳健优化模型为
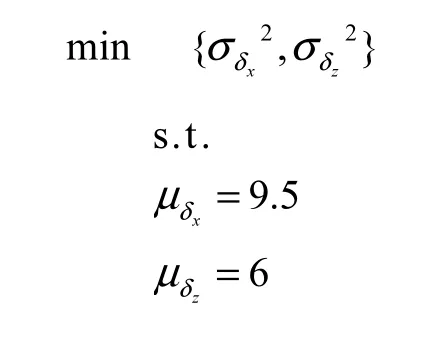

2.5 稳健优化及结果分析
设定 2个目标函数的权重分别为 0.8、0.2,代入稳健优化模型,借助自行开发的稳健设计软件进行稳健优化.稳健优化迭代曲线如图 5所示,从图中可看出优化收敛性良好.
优化结果如表 4所示.优化解使得主轴箱在满足基本性能约束的条件下,满足了基本功能需求,即使变形稳定在一个固定值上,且功能需求的方差最小.稳健优化的目的还在于降低功能需求对各个设计变量的灵敏度,从而降低加工成本.
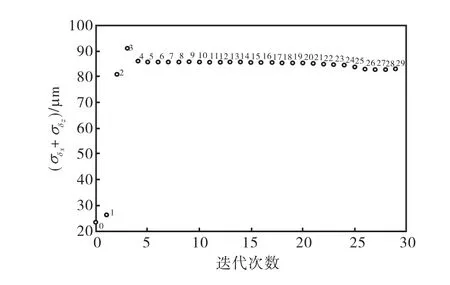
图5 优化迭代曲线Fig.5 Optimized iteration curve

表4 优化结果Tab.4 Optimization results
圆整分析值是将优化值圆整后重新进行稳健分析而来的结果,对比发现,圆整后结果的稳健性基本未发生变化,可以将此组圆整值视为最终的优化值应用.
图6为稳健设计软件界面,软件采用模块化思想,按功能分为数据编辑模块、项目管理模块、稳健处理模块、数据交换模块和DACE模块等.以上表格中的变量数据及优化结果数据均可以在数据编辑区中直接查询读取.

图6 稳健设计软件界面Fig.6 Interface diagram of the robust design software
2.6 优化结果中性能变量的有限元验证
噪声变量值取 E=2×105,MPa,设计变量取优化结果的圆整值,重新构建有限元分析模型进行分析,得性能变量验证值.比较稳健优化与有限元验证所得性能变量结果,如表5所示.

表5 稳健优化结果的有限元验证Tab.5 Finite element validation of robust optimization results
由表5可以看出,优化值处以δx的误差最大,为7.268%.根据设计要求,设计结果与实际偏差满足要求,可作为最终结果应用到实际工程中去.
3 结 论
(1) 建立了基于Kriging代理模型的分析性稳健设计方法,即“确定参数-正交试验-代理模型-稳健优化-验证”的设计过程.利用 DACE工具箱和自行开发的分析性稳健设计工具箱,已实现上述过程的有机集成.
(2) 基于Kriging代理模型建立了考虑噪声变量的多目标分析性稳健设计模型.
(3) 基于Kriging代理模型的主轴箱分析性稳健优化结果表明,各个响应变量的代理模型最大相对均方根误差5.89%;优化结果在满足各个性能约束的基础上,使得功能需求方差最小.
(4) 有限元验证结果表明基于 Kriging代理模型-分析性稳健设计方法可以得到与实际情况吻合的稳健分析及优化结果.
[1] 陈立周. 稳健设计[M]. 北京:机械工业出版社,2000.Chen Lizhou. Robust Design[M]. Beijing:China Machine Press,2000(in Chinese).
[2] Beyer H G,Sendhoff B. Robust optimization:A comprehensive survey[J]. Computer Methods in Applied Mechanics and Engineering,2007,196(33):3190-3218.
[3] 刘德顺,岳文辉,杜小平. 不确定性分析与稳健设计的研究进展[J]. 中国机械工程. 2006,17(17):1834-1841.Liu Deshun,Yue Wenhui,Du Xiaoping. Study on uncertainty analysis and robust design:A review[J].China Mechanical Engineering,2006,17(17):1834-1841(in Chinese).
[4] Gu P,Lu H,Spiewak S. A new approach for robust design of mechanical systems[J]. Annals of the CIRP,2004,53(1):129-133.
[5] Huang Beiqing,Du Xiaoping. Analytical robustness assessment for robust design[J]. Structural and Multidisciplinary Optimization,2007,34(2):123-137.
[6] Zhang Jian,Bao Nengsheng,Bao Guojun,et al. Analytical approach to robust design of nonlinear mechanical systems[J]. Frontiers of Mechanical Engineering in China,2009,4(2):203-214.
[7] 崔庆安,何 桢,车建国. 一种基于支持向量机的非参数双响应曲面法[J]. 天津大学学报,2006,39(8):1008-1014.Cui Qing′an,He Zhen,Che Jianguo. SVM-based nonparametric dual response surface methodology[J]. Journal of Tianjin University,2006,39(8):1008-1014(in Chinese).
[8] Lophaven S N,Nielsen H B,Sndergaard J. DACE a matlab Kriging toolbox[EB/OL]. http://www. Immdtu.dk/~hbn/dace/,2005-02-19.
[9] 谢延敏. 基于 Kriging模型和灰色关联分析的板料成形工艺稳健优化设计研究[D]. 上海:上海交通大学塑性成形工程系,2007.Xie Yanmin. Research on Robust Optimization of Sheet Metal Forming Based on Kriging and Grey Relational Analysis[D]. Shanghai:Department of plasticity Technology,Shanghai Jiao Tong University,2007(in Chinese).
[10] Wasim Raza,Kim Kwang-Yong. Shape optimization of wire-wrapped fuel assembly using Kriging meta modeling technique[J]. Nuclear Engineering and Design,2008,238:1332–1341.
[11] 黄风立,王艳敏,许锦泓,等. 基于关联度及 Kriging模型的注射成型稳健优化设计[J]. 中国塑料,2009,23(5):70-75.Huang Fengli,Wang Yanmin,Xu Jinhong,et al.Robust design of injection moulding based on relation degree and Kriging model[J]. China Plastics,2009,23(5):70-75(in Chinese).
[12] 高月华,王希诚. 基于 Kriging代理模型的稳健优化设计[J]. 化工学报,2010,61(3):676-681.Gao Yuehua,Wang Xicheng. Robust optimization based on Kriging surrogate model[J]. CIESC Journal,2010,61(3):676-681(in Chinese).
[13] 张 健,顾佩华,包能胜,等. 非线性机械系统分析性稳健设计[J]. 机械工程学报,2009,45(10):207-215.Zhang Jian,Gu Peihua,Bao Nengsheng,et al.Analytical robust design of non-linear mechanical systems[J]. Journal of Mechanical Engineering. 2009,45(10):207-215(in Chinese).
[14] 白 桦. 面向产品族的大型铣齿机模块化产品平台设计与优化研究[D]. 天津:天津大学机械学院,2008.Bai Hua. Study on Design and Optimization of Modular Product Platform of Large Gear Milling Machine for Product Family[D]. Tianjin:School of Mechanical Engineering,Tianjin University,2008(in Chinese).
