基于最大Lyapunov指数的市场出清电价预测

杨淑霞，徐琳茜，刘达，韩奇，张丽，丁晖

(1. 华北电力大学 经济与管理学院，北京 102206；2. 中国电监会山东电监办，山东 济南，250101)

市场出清价是体现电力商品在市场中短期供求关系的重要指标。准确预测市场出清电价一方面为发电侧竞价上网提供重要参考依据，另一方面为市场监管提供重要的科学依据，有效保证电力市场竞争健康、稳定、有序，国内外许多研究者使用不同的方法对出清电价预测进行了研究，如：文献[1]采用合作协同进化的方法进行出清电价预测；文献[2]基于历史电价、电量以及其他信息，采用神经网络法对电力市场出清电价进行预测；文献[3]从市场出清价具有非线性和多时间尺度的特性出发，采用人工免疫系统优化后的小波网络来描述市场出清价的变化规律并对次日市场出清价进行预测；文献[4]用免疫遗传算法对模糊神经网络的学习算法进行改进，对出清电价进行预测；文献[5]对市场出清电价的影响因素进行了系统分析，认为影响市场出清电价的因素众多，且这些因素具有较强的随机性和不确定性，而常规的市场出清电价单值预测模型未充分考虑历史数据的不确定性，预测结果无法体现市场出清电价的随机变化特性，预测精度也较低；文献[6]将BP神经网络引入出清电价预测，将负荷和清算电价作为输入变量，出清电价作为输出变量，构造了3层BP神经网络模型对未来出清电价进行了预测；文献[7]将相似性原理和BP神经网络相结合预测日前市场出清电价，该法尤其适用于只能获得有限原始数据的情况。由于影响电价的因素很多，电价一般被认为是一种随机变量，因此，预测市场出清电价时既要给出所预测电价的可能值，还要给出相应的概率信息。文献[8]研究了西班牙能源市场次日电价的预测问题。上述研究大多采用单一序列的研究方法而忽略了不确定因素的影响，而神经网络预测方法也有其局限性。为此，本文作者引入相空间重构和最大Lyapunov指数的计算方法，在此基础上对市场出清电价序列特性进行判定。然后，依据最大Lyapunov指数预报模式，对某电力市场 1999-01-01—1999-08-31的电价数据进行混沌时间序列判定，采用最大Lyapunov指数预报模式进行出清电价预测。最后，将预测结果与 AR(2)模型预测市场出清电价结果进行对比，以探讨应用最大Lyapunov指数对出清电价进行预测的可行性。

1 市场出清价混沌特性判定

1.1 相空间重构

相空间重构理论可以通过时间序列来分析非线性系统的混沌特性[9]，它使用非线性时间序列来研究系统的动力学行为，并将混沌理论应用于实际。这一理论表明：混沌动力学系统中任一变量的时间序列里包含确定系统状态所需要的全部动力学信息。在新的坐标系中考察某一变量的演化过程，所得到的状态轨迹能够保留原空间状态轨道最主要的特征。本文采用目前使用最广泛的延迟坐标状态相空间重构法[10]，将实际观测的时间序列数据扩展到多维的相空间，分析时间序列中所包含的系统信息。

将观测到的N个电价数据记为1个单变量时间序列x1，x2，…，xN，将其嵌入m维相空间，则m维相空间中的相点表示为：

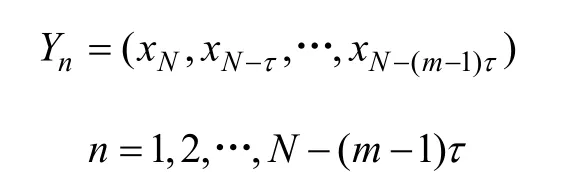
式中：N为时间长度；x1，x2，…，xN为电价序列；τ为延迟时间；m为嵌入维数。

设D0为估算的最大分数维，D为原系统的维数。根据Takens提出的嵌入定理[11]，时间长度N越大，越能反映出原系统的信息，但过大的时间长度会造成重构时间延长，因此，N通常在区间范围内取值；延迟时间τ的取值应适当，既保证各分量间的相互独立性，又要保证延迟坐标的相关性；嵌入维数m的取值应满足m≥2D+1。

1.2 混沌特性判定原理

混沌运动是一种介于确定与随机之间的更具普遍意义的状态，其产生于确定性的非线性系统中，对初始条件具有高度敏感性，并且具有自相似的分形结构和分数维。为了鉴别电价的演化过程是否为混沌运动，可采用相空间重构进行分析，提取特征指标Lyapunov指数来定量判断电价序列是否处于混沌状态。

1.2.1 最大Lyapunov指数的计算方法

Lyapunov指数是指初值不同的2条相邻轨迹在相空间中随时间推移按指数规律分离的平均发散速率，以定量描述混沌运动的初值敏感程度。Wolf[12]认为，在判断动力系统混沌运动时，只需计算最大Lyapunov指数即可。若最大Lyapunov指数为正，则系统具有初值敏感性，其运动为混沌状态；若最大Lyapunov指数等于 0，表明系统对初值不敏感，呈现周期运动；若最大Lyapunov指数为负，则系统的长期行为与初值无关，将收敛到1个平衡点。

对于一维时间序列数据，Lyapunov指数的计算可采用Wolf方法[13]，计算步骤如下。

(1) 根据实际观测的时间序列数据及样本总数N，确定延迟时间τ，构造N维空间的单变量时间序列，相点数为m=N-(m-1)τ。

(2) 选取初始相点 y0，在点集中选择最靠近y0的点yj，以y0和yj为端点构成初始向量，两端点间的欧式距离记为L(t0)(其中，t0为初始时点)。

设时间步长为 k，t1=t0+k，初始向量按t1向前演化得到新向量，该向量两端点间距离记为L(t1)，在相应时段内系统线度指数增长率为：

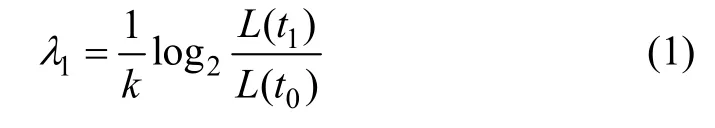
其中：λ为系统线度指数增长率。按步骤依次计算，直至所有相点为止。最大Lyapunov指数估计值为各指数增长率的平均值，即：

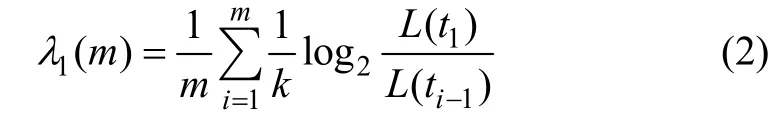
逐次增加嵌入维数n，重复以上步骤，直至λ1(m)随n变化趋于平稳为止，由此得到的计算结果即为最大Lyapunov指数。

1.2.2 市场出清价混沌特性判定结果

本文选用某电力市场 1999-01-01—1999-08-01出清电价，使用 Matlab7.0软件作为计算工具，根据文献[14]中相空间重构的Matlab程序接口，对电价序列进行相空间重构。通过Matlab编程计算，得出延迟时间τ=9，Lyapunov指数为0.037＞0，判定该时间序列具有混沌特性；由相关系数选择Lyapunov指数均大于 0，说明短期内出清电价的演化过程对初始条件具有敏感依赖性，电价序列初值的微小变化将随时间推移呈指数增长。此外，Lyapunov指数较小，电价的演化速率较慢，电价序列演化过程的短期预测可以实现。

2 基于最大Lyapunov指数的出清电价预测

2.1 基于Lyapunov指数的预报模式

取初始相点为Y(t0)，搜寻Y(t0)的最近邻点Y0(t0)，设2点距离为L0，考察这2点的时间演化过程，直至这2点间距超过规定值ε为止，此时，时点为t1。令，在Y(t1)附近另寻点Y1(t1)，使得，且 Y0(t1)-Y(t1)与 Y1(t1)-Y(t1)之间的夹角尽可能小；重复上述过程，经过M次迭代后，此时，时点为 tM，Y(t)到达时间序列构成的相空间终点，由此得到的最大Lyapunov指数为：

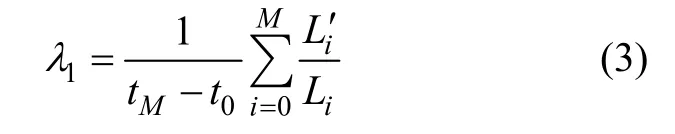
其中：Li为 Y(ti)与其最近邻点 Yi(ti)间的距离；Li′为Y(ti+1)与 Yi(ti+1)间的距离；i=0，…，M。在不同步长的演化过程中， Li′ / Li近似为常数，这一特性为建立基于最大Lyapunov指数的预报模式奠定了基础[15]。

设Y(ti)为预测的中心点，计算其最近邻点Y(tj)，经过时间尺度 T后的演化相点分别为 Y(ti+T)和Y(tj+T)。若T≤τ，则相点Y(ti+T)只有第1个分量x(ti+T)是未知的，可进行预报。取 T=1，最大 Lyapunov指数为λ1，则基于最大Lyapunov指数的预报模式为：

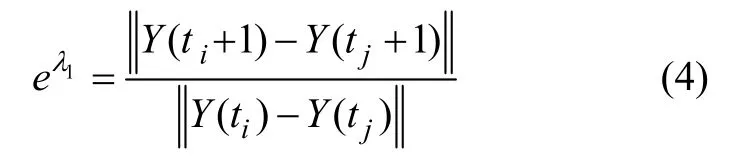
最大可预测时间尺度通常为 Tmax= 1 /λ1。T的取值具有重要意义，若其大于提前预报时间，则可以对所预测对象进行预测；若其小于提前预报时间，则所预测对象不可预测或误差超出允许值。

2.2 预测步骤

根据上述基于最大Lyapunov指数预测模式，计算某电力市场 1999-01-01—1999-08-31出清电价的Lyapunov指数。通过 Matlab编程计算，得到出清电价序列的嵌入维数m=9，最大Lyapunov指数λ=0.037＞0，验证了该电价序列为混沌时间序列，可以采用最大Lyapunov指数预报模式进行出清电价预测。

基于最大 Lyapunov指数的混沌时间序列模型预测的具体流程如图1所示，其实测值与预测值如图2所示。

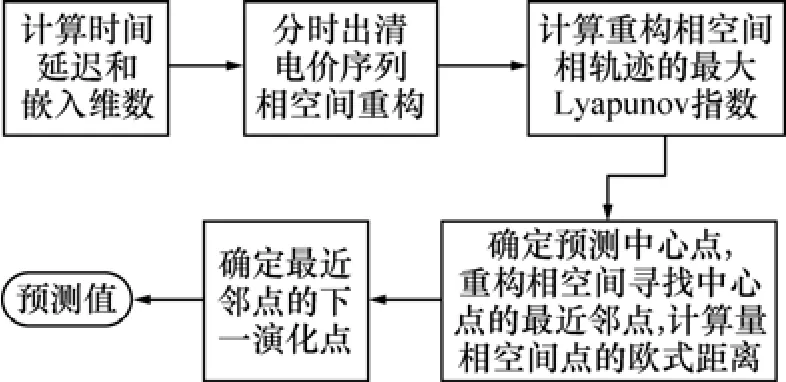
图1 混沌时间序列模型预测流程图Fig.1 Flow chart of chaos time series forecasting model

3 市场出清价预测与分析

3.1 基于最大Lyapunov指数的预测结果及分析

根据表1所示的预测结果，通过计算得出：采用Lyapunov指数预测模式进行出清电价预测，得到的预测值和实际值之间的平均绝对误差率为7.234 7%，最大绝对误差率为17.017 5%，绝对误差率大于6%的点占了1/2。从图3可以看出：出清电价预测误差率在误差为0的两侧呈现较均匀分布。

从表 1、图 2和图 3所示的预测结果可见：Lyapunov指数预测模式的平均绝对误差率为7.234 7%，误差在评价误差两侧呈现较均匀分布，最大绝对误差率为17.017 5%，大于6%的点占了1/2。

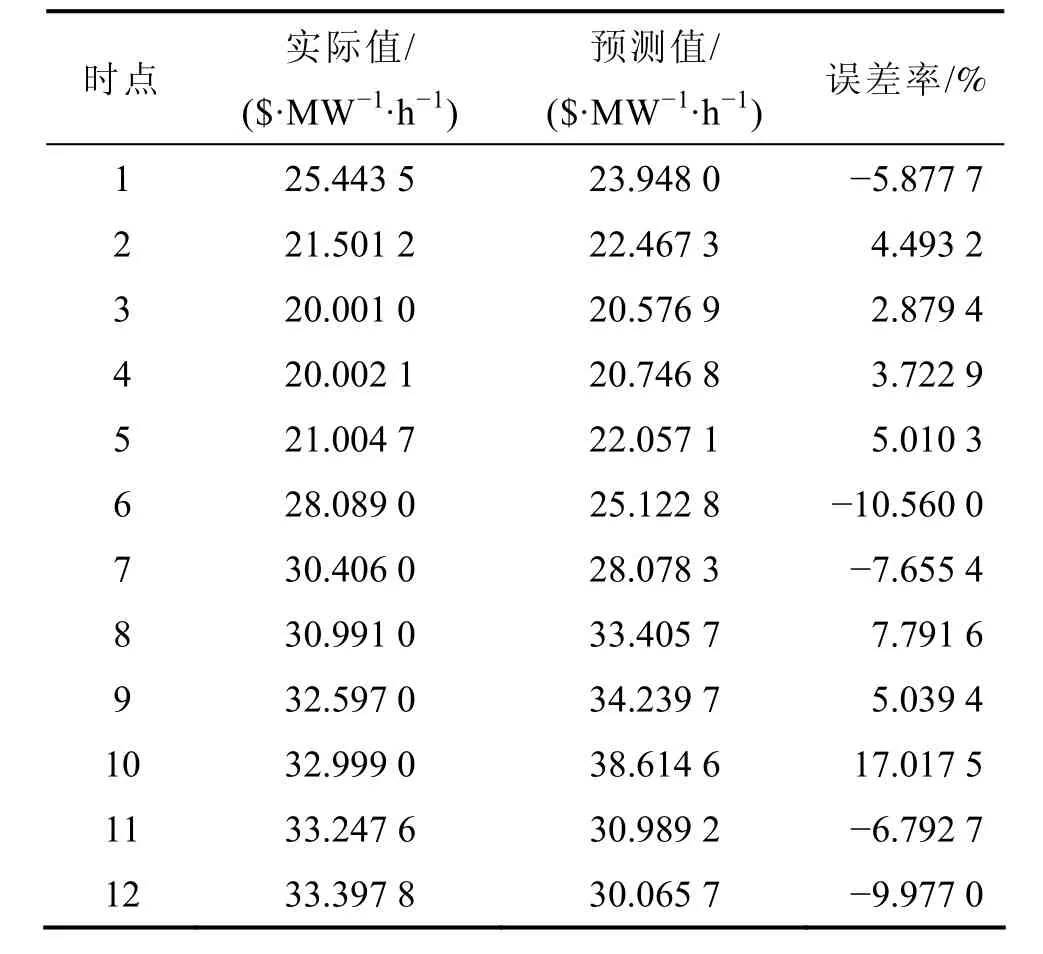
表1 Lyapunov指数预测结果Table 1 Results of Lyapunov exponent forecasting

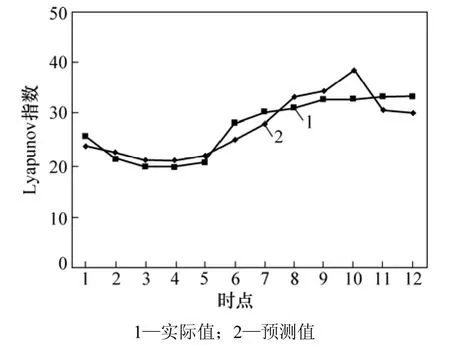
图2 基于Lyapunov指数的实测值与预测值曲线Fig.2 Curves of actual value and forecasting value based on Lyapunov exponent

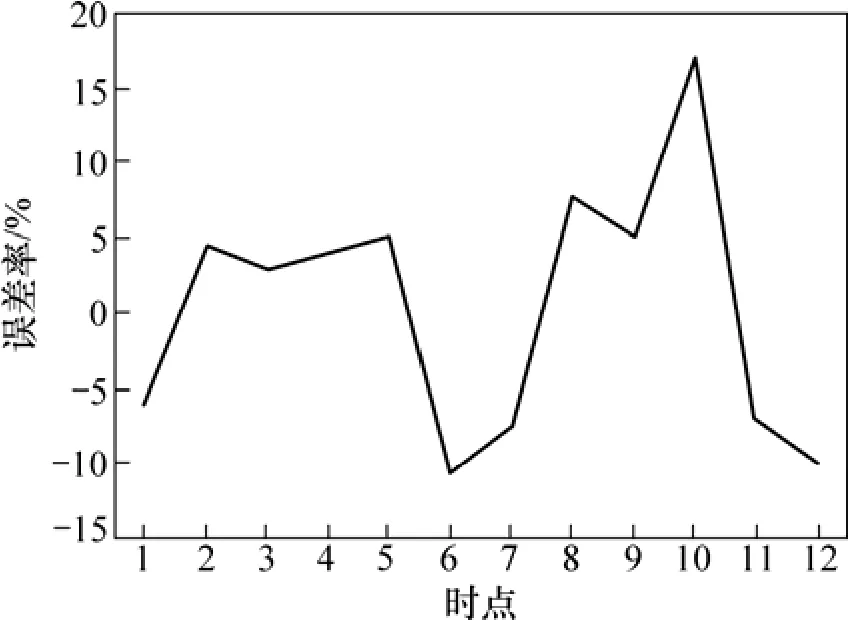
图3 基于Lyapunov指数的实测值与预测值误差率曲线Fig.3 Curve of error rate between actual values and forecasting values based on Lyapunov exponent

采用最大 Lyapunov指数预测模式进行出清电价预测时，前5个时段的预测精度比较高；随着时间的推移，预测精度不断降低。这是因为出清电价的预测受到多种因素的影响，波动非常复杂。在预测过程中，所有预测值都是基于同一嵌入维数的相空间以及相同的最大Lyapunov指数得到的。最大可预测时间尺度为1/λ=1/0.037=27.027，即最大可预测时间为27。本文为了保证预测精度，选取了12个时点进行内预测。

3.2 基于AR(2)模型的预测结果及分析

研究基于最大Lyapunov指数的预测模式的精度，将上述预测结果与文献[15]中利用 AR(2)模型预测市场出清电价的结果进行对比。

使用相同的历史数据，利用 AR(2)模型预测市场出清电价时，前12个时段刚好有6个时点为平稳性时间序列，6个时点为非平稳时间序列。每个预测模型只用来预测第2天各自对应时段的出清电价，分别得到12个时段的电价预测结果，然后，将这12个时段电价预测结果组合起来，如表 2所示。基于最大Lyapunov指数预测模型的实测值与预测值见图2，其误差率见图 3。基于 AR(2)模型的实测值与预测值及其误差率曲线分别见图4和图5。

根据表2所示的预测结果，通过计算得出：平衡电价序列构造的 AR(2)模型具有较高的预测精度，市场出清电价预测值与实际值之间的平均绝对误差率为4.571 7%，但是，非平衡电价预测值与实际值之间的平均绝对误差率为6.510 0%。这是由于电价的随机波动性较强，一般很难有效地去除电价时间序列的非平稳过程，从而在一定程度上影响了预测的效果，使得绝对误差率大于6%的点占了7/12。

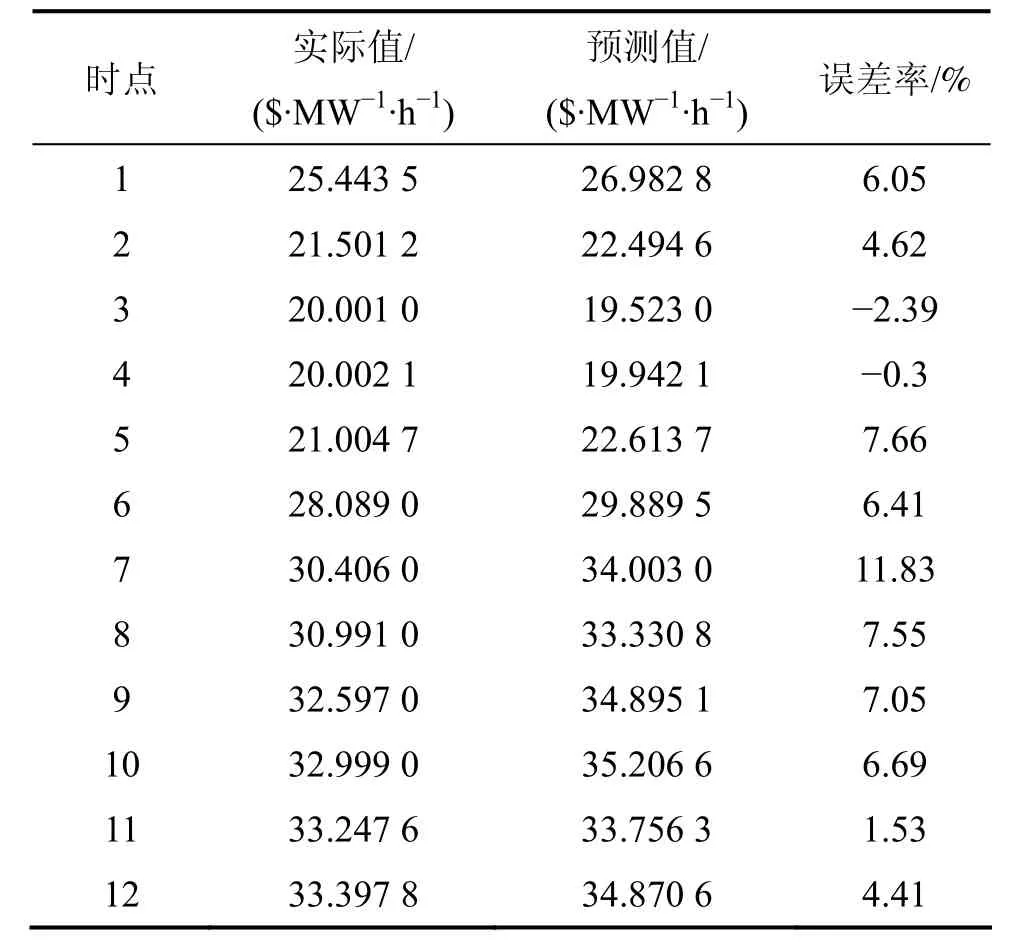
表2 AR(2)模型预测结果Table 2 Results of AR(2) model forecasting

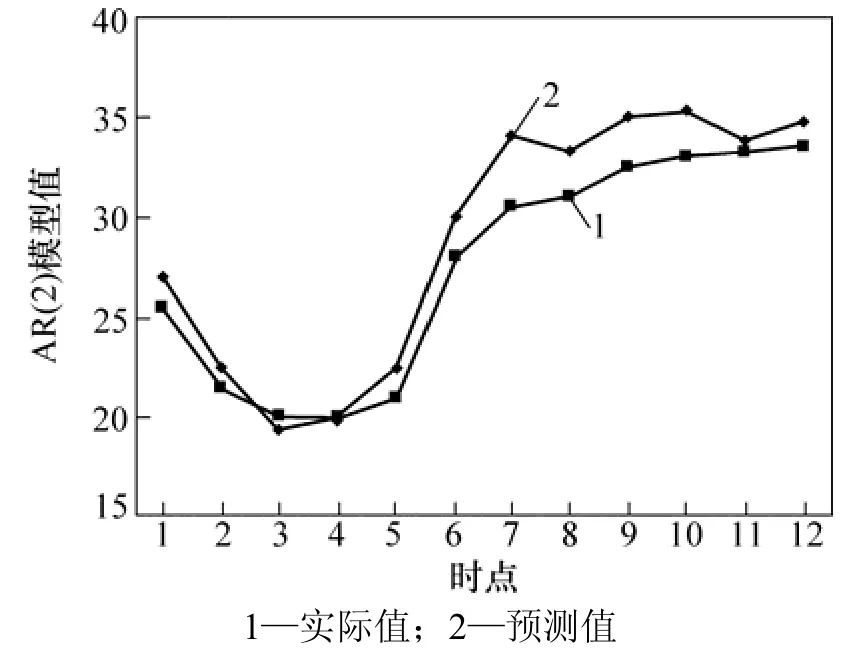
图4 基于AR(2)模型的实测值与预测值曲线Fig.4 Forecasting fitting chart curves of actual value and forecasting value based on AR(2)model

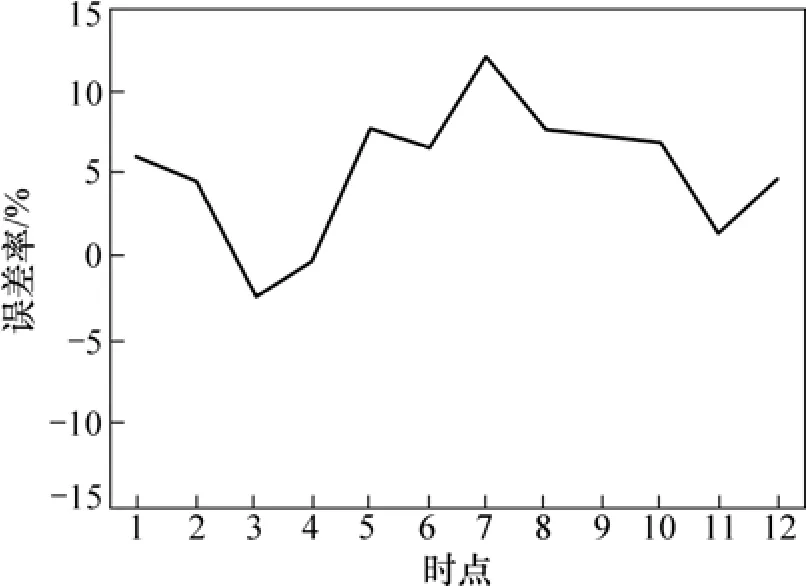
图5 基于AR(2)模型的实测值与预测值误差率曲线Fig.5 Curve of error rate curve of error rate between actual values and forecasting values based on AR(2) model

3.3 最大Lyapunov指数预报模型与AR(2)模型的预测结果对比分析

AR(2)模型预测法应用于平稳电价序列预测时精度比较高，但是，在对非平稳电价序列预测时，由于不确定性的影响加大，其平均绝对误差率较大。

出清电价序列的演化过程具有混沌特性，可采用基于 Lyapunov指数的时间序列预测模型进行预测。采用最大Lyapunov指数预报模型进行电价预测，其预测结果的总体精度略低于 AR(2)模型的预测结果总体精度，但其精度相对稳定，绝对误差率大于 6%的时点数少于后者。这说明基于最大 Lyapunov指数的市场出清电价预测是有效的。

4 结论

(1) 应用最大Lyapunov指数预测模型预测出清电价时，其最大预测时间 Tm= 1 /λ，在最大预测时间范围内进行预测均可以保证预测的准确性。在预测计算前可根据λ确定预测精度范围。在预测过程中，所有的预测值都是基于同一嵌入维数的相空间以及相同的最大 Lyapunov指数得到的，但是，预测精度随时间降低。

(2) 最大Lyapunov指数反映了相空间中相体积收缩和膨胀的几何特性。该预测方法以数据序列本身所计算出来的客观规律进行预测，有效降低了各种主观因素的影响。

(3) 最大Lyapunov指数预测模型的计算能够通过Matlab编程实现，且具有较强的可移植性和可扩展性。但采用Wolf方法的计算量较大，这有待进一步改进。

[1] Karsaz A, Mashhadi A R, Mirsalehi M M. Market clearing price and load forecasting using cooperative co-evolutionary approach[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(5): 408-415.

[2] Singhal D, Swarup K S. Electricity price forecasting using artificial neural networks[J]. International Journal of Electrical Power & Energy Systems, 2011, 33(3): 550-555.

[3] 左幸, 马光文, 梁武湖, 等. 基于人工免疫系统小波网络的电力市场出清价预测[J]. 水力发电, 2006, 32(1): 1-15.ZUO Xing, MA Guang-wen, LIANG Wu-hu, et al. The immune wavelet network model and its application to the prediction of market clearing price[J]. Water Power, 2006, 32(1): 1-15.

[4] 李彦斌, 李存斌, 杨尚东. 基于免疫遗传算法改进 DFNN 模型及其应用[J]. 中南大学学报: 自然科学版, 2008, 39(2):345-349.LI Yan-bin, LI Cun-bin, YANG Shang-dong. A new DFNN improved by artificial immune-genetic hybrid algorithm and its application[J]. Journal of Central South University: Science and Technology, 2008, 39(2): 345-349.

[5] 王高琴, 沈炯, 李益国. 基于聚类和贝叶斯推断的市场出清电价离散概率分布预测[J]. 中国电机工程学报, 2007, 27(34):90-95.WANG Gao-qin, SHEN Jiong, LI Yi-guo. Forecasting of MCP’s discrete probability distribution based on clustering and bayesian method[J]. Proceedings of the CSEE, 2007, 27(34): 90-95.

[6] 张明光, 李艳. 基于BP神经网络的下一交易日出清电价预测[J]. 电力系统保护与控制, 2009, 37(5): 18-21.ZHANG Ming-guang, LI Yan. Method for forecasting next-day market clearing prices based on BP neural network[J]. Power System Protection and Control, 2009, 37(5): 18-21.

[7] 李彦斌, 李存斌, 宋晓华. 改进的人工智能神经网络预测模型及其应用[J]. 中南大学学报: 自然科学版, 2008, 39(5):1054-1058.LI Yan-bin, LI Cun-bin, SONG Xiao-hua. Prediction model of improved artificial neural network and its application[J]. Journal of Central South University: Science and Technology, 2008,39(5): 1054-1058.

[8] Raúl P, José P. Forecasting next-day price of electricity in the Spanish energy market[J]. Engineering Applications Txt of Artificial Intelligence, 2007, 21(1): 53-62.

[9] 鄂加强, 王春华, 彭雨, 等. 混沌特性时间序列线性变换理论方法及其应用[J]. 湖南大学学报: 自然科学版, 2008, 36(2):36-42.E Jia-qiang, WANG Chun-hua, PENG Yu, et al. Analysis and application of the chaos character of time series after linear transformation[J]. Journal of Hunan University: Natural Sciences,2008, 36(2): 36-42.

[10] Aghaei J, Shayanfar H, Amjady N. Multi-objective market clearing of joint energy and reserves auctions ensuring power system security[J]. Energy Conversion and Management, 2009,50(4): 899-906.

[11] Zhang T, Elkasrawy A, Venkatesh B. A new computational method for reactive power market clearing[J]. International Journal of Electrical Power & Energy Systems, 2009, 31(6):285-293.

[12] Wolf A. Determining Lyapunov exponents from a time series[J].Physica D: Nolinear Phenomena, 1985, 16(3): 285-317.

[13] 吕金虎, 陆君安. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2002: 64-95.LÜ Jin-hu, LU Jun-an. Analysis and application of chaotic time series[M]. Wuhan: Wuhan University Press, 2002: 64-95.

[14] 万武辉. 利用混沌时间序列预测技术进行电力市场短期电价预测[D]. 成都: 电子科技大学计算机科学与工程学院, 2005:40-50.WAN Wu-hui. Power market price forecasting based on Chaotic time series prediction[D]. Chengdu: University of Electronic Science and Technology of China. School of Computer Science and Engineering, 2005: 40-50.

[15] 张丽. 市场出清价规律分析与预测[D]. 北京: 华北电力大学经济与管理学院, 2007: 26-39.ZHANG Li. Analysis and forecast of the market clearing price law[D]. Beijing: North China Electricity Power University.School of Economics and Management, 2007: 26-39.