电离层探测仪回波能量积累算法

李汛江，苏凡凡，赵正予

(1. 武汉数字工程研究所，湖北 武汉，430074；2. 武汉大学 电子信息学院，湖北 武汉，430079)

常用的电离层底测方法有垂直探测、斜向探测、斜向返回散射探测及直接散射探测等。这些探测技术可探测电离层的状态信息[1-3]，还可能获取广大范围内的海洋状态信息和高频无线信道参数[4-5]，以提高对电离层状态、物理过程以及电离层电波传播规律的基本认识，揭示电离层动力学及形态学的地域特征和电离层信道特性，还可用于描述和预报电离层状态，并可为电离层电波传播链路提供信道状态实时预报，提高短波通信的可靠性和准确性，用于超视距目标定位等。美国 Lowell大学大气研究中心研制的数字电离层测高仪DPS-4D是现在较先进的电离层探测设备之一[1]，主要工作模式为垂测探测，它采用脉内相位编码的数字脉冲压缩等技术，在世界各地设有大量垂测站点。澳大利亚的JINDALEE雷达通过斜向探测和斜向返回探测获取高频信道的信道特征信息[6]，实现对实时频率管理的指导。武汉大学电离层实验室自主研发了具有垂测、斜测和斜向返回探测功能的 WISS雷达组[7-9]，可用于电离层诊断和短波信道链路状态分析等。工作在短波段的电离层探测仪容易遭受到其他高频用户和无线电噪声的干扰，这增加了各种探测模式下电离层回波的检测难度。斜向返回回波经过电离层反射和地面后向散射后，会遭受到很大的衰减和损耗，其信噪比的典型值一般其他探测模式的更小。雷达的小型化和便携化需求对信号处理的积累增益也提出了更高的要求。本文作者设计一组电离层探测仪回波预处理能量积累算法。首先以脉间相位编码为例分析了脉冲压缩算法；然后，基于多次探测的相位连续性，使用了多普勒积累算法；最后，基于电离层回波的散布特性开发了时延多普勒域的二维积累算法，用各种积累算法处理实测数据后信噪比的变化。

1 能量积累算法

1.1 算法运行平台

因电离层探测仪的便携化需求而研发的预处理能量积累算法主要在武汉大学电离层实验室研发的WISS雷达组的信号处理系统中实现。WISS雷达组由具有垂测探测、斜向探测和斜向返回探测功能的多部雷达组成，部署在湖北武汉、广西钦州等地区。这些雷达均采用了数字频率合成(DDS)和数字下变频(DDC)等先进技术，由控制系统的软件控制伪随机码序列产生、信号发射和回波接收和处理等工作流程，易于实现探测模式和波形的调整，可以根据实时电磁环境状况调整探测参数，优化目标检测性能，诊断电离层状态和短波信道特征。

雷达组中各部雷达均采用FPGA产生伪随机码序列并控制DDS生成发射波形，经放大滤波后发射。接收到的回波在解调后进行A/D采样，再输送到 DDC抽取滤波，输出回波的同相分量I和正交分量Q，信号的幅度信息和相位信息即可获取，然后，输入到信号处理系统中提取目标特征。

高频电波在传播过程中会遭受自由空间传播损耗和电离层吸收损耗，在接收端也存在额外系统损耗等，多径效应和多普勒效应会引起回波能量散布，斜返回波还会遭受地面后向散射损耗。短波段的干扰和噪声源很丰富，而雷达组采用了低功率发射机，多种原因导致回波脉冲一般会淹没在噪声背景中，需要预处理才能显现。通常先将接收到的回波序列进行积累预处理，然后对积累结果进行检测判决，获取回波信号位置和其他信息。虽然信号和噪声均会累积，但若信号功率与噪声功率之比大于积累前的信噪比，则可以提高信号的检测概率。

1.2 脉冲压缩积累算法

脉冲压缩可通过发射宽编码脉冲并处理接收回波获得窄脉冲实现。使用了脉冲压缩技术的雷达既保持了宽脉冲雷达的强检测能力，也获得了窄脉冲的高距离分辨率。WISS雷达组采用的脉间伪随机码调相是脉冲压缩的实现方式之一。脉间调相体制与常用的脉内调相体制的主要区别在于：脉间体制在同一次探测过程中，接收和发射可同时进行，由特别研发的开关电路保护接收机；而脉内体制在同一次探测过程中，前一段时间用于发射，后一段时间用于接收，实行分时保护接收机。探测体制的差异导致了盲区在回波域中的分布方式不同，脉内调相体制的盲区主要分布在回波的前一部分群时延路径上，盲区的覆盖区域由脉冲重复频率确定，而脉间调相体制的盲区均匀分布在整个回波域中，盲区的宽度由子脉冲重复频率确定。若需要通过增加脉冲压缩比来增加积累增益，提高回波信噪比，则需要增加伪随机码的码长，同时会增大脉冲重复周期。由于脉间调相体制的盲区是均匀分布在整个回波域中的，增加脉冲压缩比不会影响盲区的大小。而脉内调相体制盲区的大小与脉冲重复周期成正比，其脉冲压缩比的增大受到探测盲区的限制。因此，WISS雷达组采用了脉间调相的脉冲压缩方式，可使用更长的码长和更高的脉冲压缩比实现单基地小功率远距离探测。

脉间调相体制和脉内调相体制的实现方式也有差异，脉内调相体制的实现方式可以参考相关手册[10]。脉间调相体制的数据处理流程如图1所示，图中虚线框中所示的模块的功能为按子脉冲重复周期提取回波，这是脉间调相体制与脉内调相体制实现方式的不同之处。

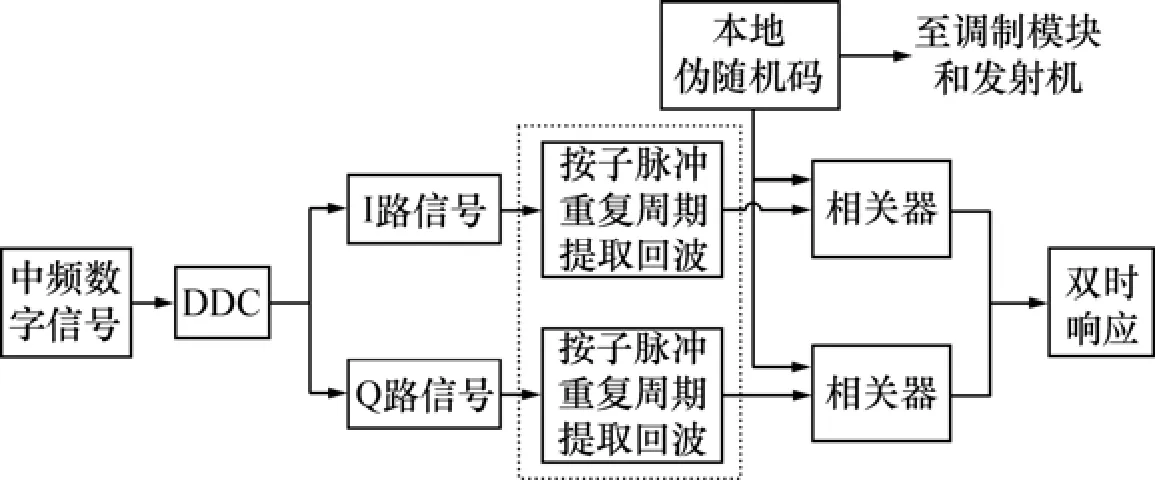
图1 脉间调相体制的数据处理流程图Fig.1 Data process flowchart for intra-pulse phase coded radar

假设p(k)(k=1，…，M，M为码长)为本地伪随机序列，接收信号s1(k)由回波信号序列s(k)和噪声序列n(k)组成，即s1(k)=s(k)+n(k)。脉冲压缩的累积过程可以表示为：

脉冲压缩积累的输出由2部分组成：一部分是本地伪随机序列和回波序列的相关运算。由于本地伪随机序列和回波序列是相位相参的，根据图1的实现过程及伪随机序列的特性可知[11]，相关运算后回波信号的幅度会增加M倍。另一部分是本地伪随机序列和噪声的相关运算，噪声与本地序列是非相位相参的，在本地伪随机序列的加权累加下，其幅度增加倍。因此，在理想条件下，信号与噪声的幅度比将增加倍。多次探测的回波信号经过脉冲压缩积累后成为双时响应数 据[11]，是回波信号在群时延-时间域的表现。

1.3 多普勒积累

电离层探测雷达回波的散射体为电离层不均匀体，不均匀体的运动使回波相位畸变，导致回波信号相对于发射信号产生多普勒频移。采用相位编码体制时，回波相位的畸变会影响解调后的回波序列，使回波序列与本地伪随机序列的相关峰削弱，并抬高旁瓣。但是，电离层的运动特征可从多普勒信息中推导获取，高频信道的时间色散特性也可由多普勒信息确定。因此，需要既能保存多普勒信息，也能实现积累效果的算法。本文提出的实现过程为对该频点探测多次，然后，对同一群时延距离上的多次探测回波实现多普勒积累，在多普勒域中回波能量会集中到多普勒频移附近区域，而噪声能量依然分散在整个多普勒域中，信噪比得以提高。

脉冲压缩积累后的回波表达式为 y1(τ)，τ表示回波时延。多次探测的结果可以记为 y1(τ，n)，其中，n=1，2，3，…，N，其意义是实现了连续N次探测。用信号与噪声之和的形式描述y1(τ，n)，可得：

其中：s2(τ)表示回波的幅度；fd表示信号的多普勒频移；表示探测时间；f表示脉冲重复频率；N(τ，n)表示脉冲压缩积累后的噪声。对 y1(τ，n)实现多普勒积累的过程为：多次探测的回波乘以全频段的单位幅度的复正弦波，然后对处理结果累积相加。这个过程的数学表述为：

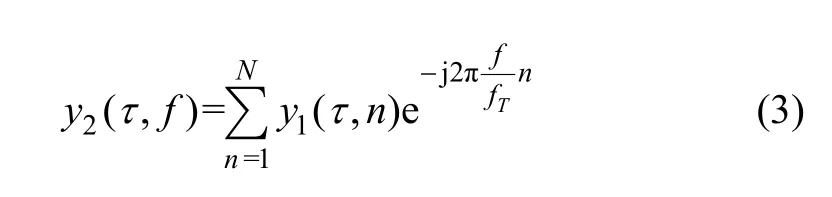
由于电离层信道可以在短时间内保持稳定，可以认为信号s2(τ)在N次探测的过程中保持不变。将式(2)中的y1(τ，n)代入式(3)可以得到：

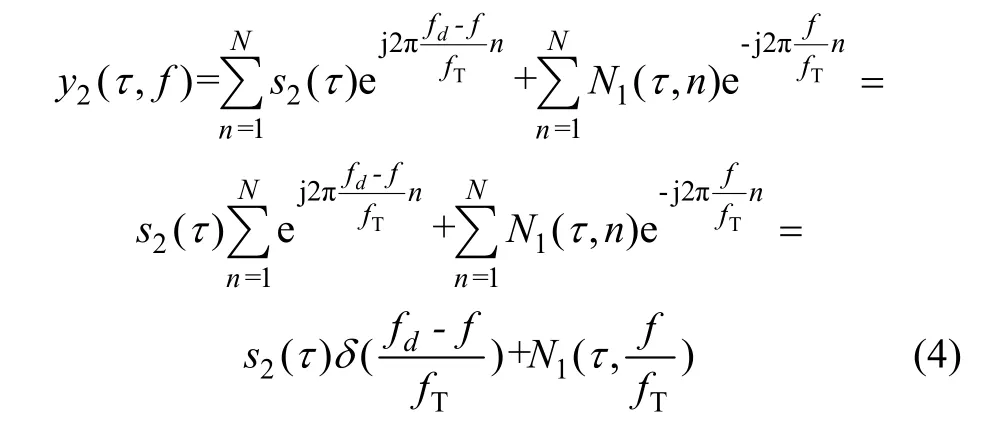
由式(4)可知，多普勒积累的结果是将多次探测的信号的能量集中到了频移为fd的多普勒域上，而多次探测的噪声能量依然分布在整个多普勒域中。理论上，积累使回波能量增强了20lg(N)。回波信号经过多普勒补偿积累后获取的结果为散射函数数据[11]，是回波信号在群时延-多普勒域的表现。多普勒补偿积累不仅能提高回波信噪比，还能保留多普勒信息，用于推演电离层运动特征和高频信道的时间散布特性。

1.4 群时延-多普勒域二维积累算法

由于电离层回波由位于不同距离和具有不同运动速度的不均匀体反射，探测雷达接收到的回波在群时延距离和多普勒域上均有散布。多普勒补偿积累后，信号能量并非积累到一点，而是连续分布在群时延-多普勒域的一片区域中，即具有区域连续散布特性。由于脉间调相体制会将探测盲区均匀分散到整个回波域内，回波在群时延-多普勒域中的表现形式为：回波散布在群时延-多普勒域的一片区域中，此区域中会出现间隔的回波盲区。这些回波盲区可借助群时延-多普勒域二维积累算法基于电离层回波的区域连续散布特性补偿。对于非脉间调相体制，短波信道的衰落特性会导致回波区域内出现幅度起伏，其中，弱回波区可使用此算法实现能量增强。

群时延-多普勒域二维积累算法使用二维加权函数处理回波域。此算法是从数字图像处理技术[]的膨胀算法中衍生的[12]。这种积累技术的数学表述如下：

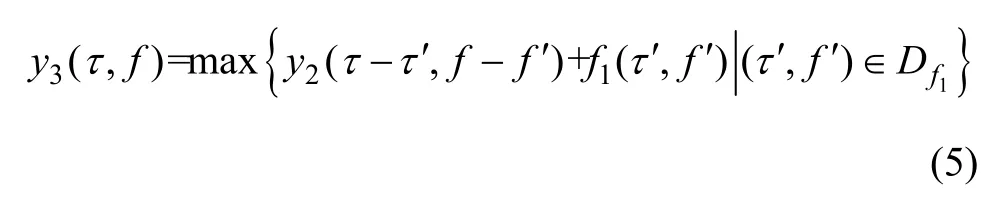
其中：f1(τ，f)为二维加权函数； Df1为 f1(τ，f)的定义域。

算法的处理过程为：将二维加权函数f1(τ，f)在整个群时延-多普勒域中平移；然后，在每个平移位置使加权函数与当前定义域内的回波值相加，取出其中的最大值，作为二维积累后的结果，记为y3(τ，f)。在回波去噪后使用此算法处理，位于回波之间的无信号区在周围信号的加权下会填入信号。这种积累算法不仅可弥补回波区域中的随机幅度衰落，还可填补脉间调相体制的固有盲区，具有很高的实用价值。

电离层回波经多种积累算法处理后，回波信噪比将得到很大的提高，有利于回波的自动检测。通过自动检测技术获取回波位置信息之后，就能实现多普勒信息的自动提取，并实时获取电离层运动状态及高频信道时间色散特性[13-15]。

2 实测数据处理

WISS雷达组中的各部雷达均可以获取回波的幅度和相位信息，可作为上述积累算法的验证平台。图2所示为对WISS雷达组的实测数据使用脉冲压缩积累算法处理的效果，回波数据在 2010-09-06日上午湖北武汉城区获取，实验中采用8阶m序列调相波形，78 μs的子脉冲宽度，并以100 W的峰值功率发射64组脉冲串，工作频率为6.2 MHz。图2(a)所示为从接收机直接获取的脉冲波形，信号与噪声能量接近，无法确定是否出现电离层回波。图2(b)所示为脉冲压缩积累后的回波数据，在400 km左右出现明显的回波峰，充分展示出脉冲压缩积累的效果，综合其他频点的回波可判定为F层垂测回波。这表明脉冲压缩积累不仅能提高回波信噪比，也是提取回波群时延距离信息的有用方式，为电离图的判读提供基础信息。图2(c)所示为脉冲多普勒积累后的回波数据，信噪比与子图(b)的相比有所增强。

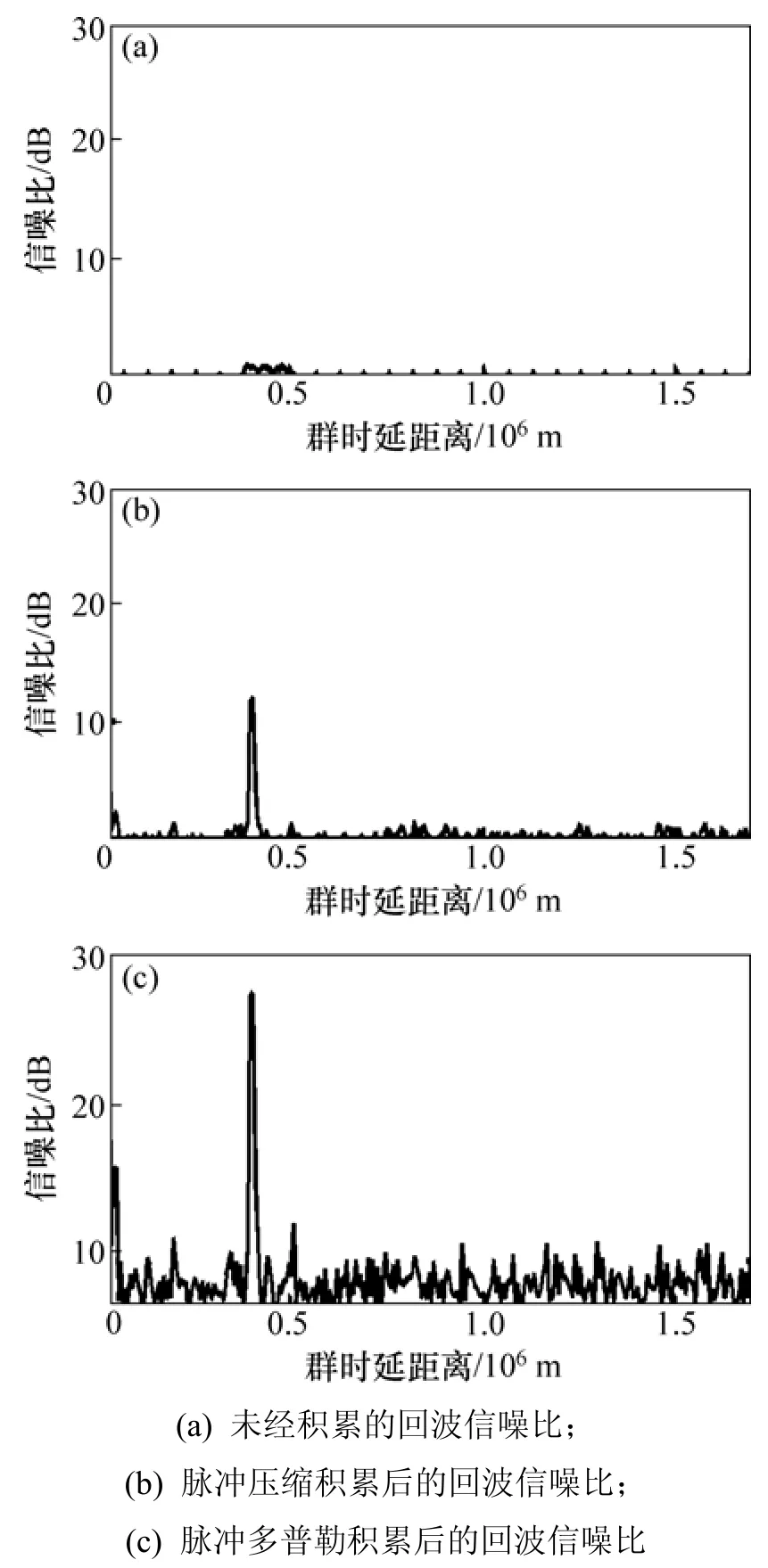
图2 信噪比随群时延距离的变化Fig.2 Change of SNR with group path

图3 所示为多普勒积累算法处理的效果，回波数据在同一时间同一地点获取，采用的波形体制与也图2的相同，工作频率为11 MHz。武汉城区的电磁环境较差，获取的电离图中不仅干扰多，底噪也很高。由图 3(a)无法判读是否有回波信号存在。图3(b)中信号与噪声混杂，脉冲压缩积累后仍然无法判断是否有回波出现。图 3(c)充分展示了多普勒积累的效果，可以在1.2×106m左右看到图3(b)中无法识别的回波峰，综合其他频点信息判定为斜返回波，充分展示了多种积累算法的联合应用在低功率探测仪中的必要性。这种多普勒积累方法还可获取回波的多普勒信息，图 2中回波信号的多普勒频移为0.48 Hz，当时的电离层漂移速度为23.2 m/s。在图3中回波信号的多普勒频移为-0.72 Hz，经过其他算法处理后可以为短波信道特征诊断提供依据。

图4所示为2007-12-25T15:44在海南万宁郊区探测的定频斜向返回的回波数据。探测仪工作频率为11.3 MHz。图4(a)所示为双时响应图，是经过脉冲压缩积累算法处理后的回波信噪比随探测时间和群时延距离变化的二维图，从图中的灰度条可知信噪比很低；回波间也存在功率与噪声基底功率相近的盲区。图4(b)所示为多普勒积累算法处理后的散射函数图，通过与图 4(a)的灰度条对比可见，信噪比有了很大的提高，但盲区依然存在，并将本应连续的回波区域切成多块区域。处理后的回波数据已变换到群时延-多普勒域中，可使用群时延-多普勒域二维积累算法。由算法原理可知，回波最大信噪比不会改变，但弱回波会增强。图 4(c)所示为群时延-多普勒域二维积累后的效果，弱回波能量更强，盲区也基本消失，更完整的回波区域覆盖图显现在散射函数图中。

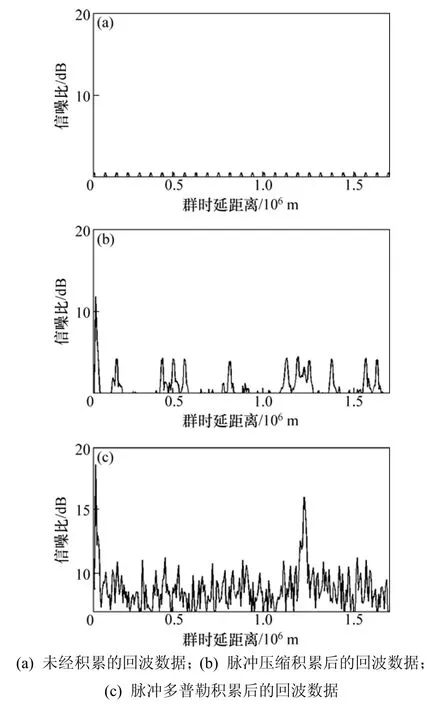
图3 信噪比随群时延距离的变化Fig.3 Change of SNR with group path

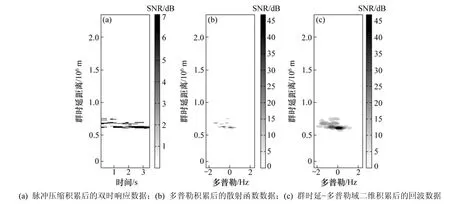
图4 信噪比随群时延距离和时间/多普勒的二维变化图Fig.4 Change of SNR with group path and time/Doppler

WISS雷达组在2007-12-24T08:53在海南万宁郊区获取了一组斜向返回扫频回波数据，如图5所示。探测波形为 9阶 m序列脉间调相波形，扫频范围为6～11 MHz，扫频步进为0.1 MHz，探测次数为16次。将各个频点的数据按脉冲重复周期进行幅度积累处理，为非相干积累[16]，信噪比增益较低。图5(a)所示为对各个频点的数据多普勒积累获取的，较多的回波显现出来了，但是，由于盲区和衰落的影响，覆盖区域特征并不明显。图5(b)所示为时延-多普勒域二维积累后的效果，补偿了盲区，斜返回波的区域覆盖特征得到强化，有利于后期的斜返回波区域特征提取。

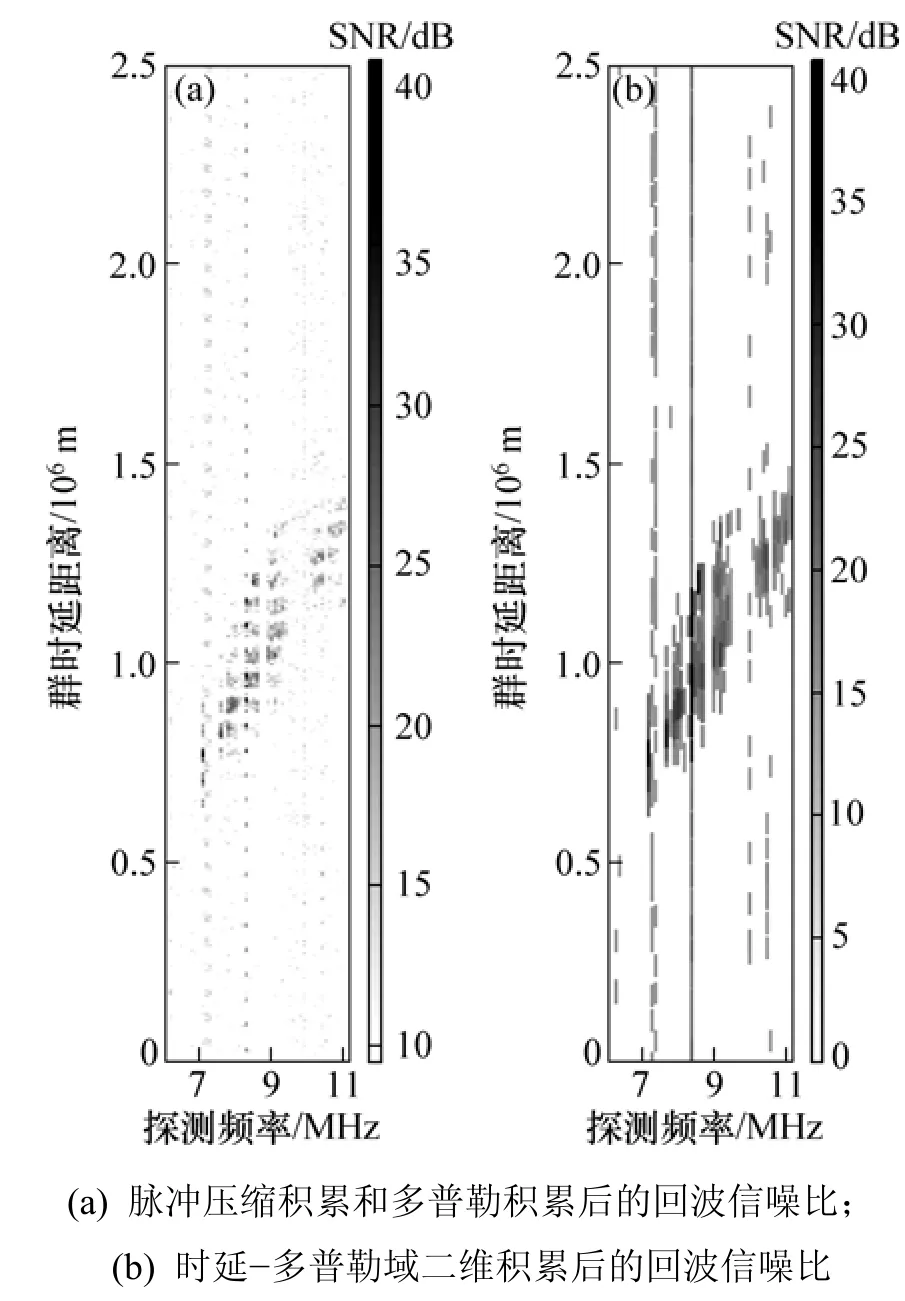
图5 信噪比随群时延距离和探测频率的二维变化图Fig.5 Change of SNR with group path and operating frequency

实测数据的处理效果充分展示了多种积累方式的有用性。以往的电离层探测仪发射功率大，且由于使用了脉内调相体制或调频连续波体制，存在大范围的探测盲区，WISS雷达组可使用更长的伪随机码实现更好的积累效果，充分发挥脉间调相体制雷达的优势。WISS雷达组的回波具有相位连续性，可实现有效的多普勒积累。回波均匀散布的盲区也通过时延-多普勒域二维积累算法得到有效补偿。积累算法要求处理前的回波数据包含幅度和相位信息，以实现脉冲压缩和多普勒补偿积累的相干累积效果。时延-多普勒域二维积累的非相干积累技术增强了回波，有利于回波覆盖区域的识别，填补可能出现的回波衰落，补偿了脉间调相体制的均匀分布盲区。多种积累方式在垂直探测、斜向探测和斜向返回探测中均可使用，现已应用在WISS雷达组的信号处理分系统中。

3 结论

(1) 预处理能量积累算法是雷达回波自动检测和提取回波信息的基础。本文讨论的积累算法组目前在武汉大学电离层实验室研发的所有电离层探测仪中使用，并适用于所有能够提供回波的幅度和相位信息和相位具有连续性的雷达。

(2) 脉冲压缩积累和多普勒积累 2种相干积累方式均可以显著提高回波信噪比，回波群时延距离和多普勒信息在积累后分别显示在双时响应和散射函数图中。时延-多普勒域二维积累的非相干积累方式增强了斜返回波的区域覆盖特征，补偿了脉间调相编码体制雷达的均匀散布盲区。这些积累算法效果好，易实现易推广，对雷达设备的小型化和便携化发展具有实用价值。

[1] Zong Q G, Reinisch B W, Song P, et al. Dayside ionospheric response to the intense interplanetary shocks-solar wind discontinuities: Observations from the digisonde global ionospheric radio observatory[J]. Journal of Geophysical Research: Space Physics, 2010, 115(A6): A06304.

[2] Chen G, Zhao Z, Zhou C, et al. Solar eclipse effects of 22 July 2009 on Sporadic-E[J]. Annales Geophysicae, 2010, 28(2):353-357.

[3] Benito E, Bourdillon A, Saillant S, et al. Inversion of HF backscatter ionograms using elevation scans[J]. Journal of Atmospheric and Solar: Terrestrial Physics, 2008, 70(15):1935-1948.

[4] Vilella C, Miralles D, Altadill D, et al. An Antarctica-to-Spain HF ionospheric radio link: Sounding results[J]. Radio Science,2009, 44(2): RS2014.

[5] Warrington E M, Stocker A J, Siddle D R. Measurement and modeling of HF channel directional spread characteristics for northerly paths[J]. Radio Science, 2006, 41(2): RS2006-1-13.

[6] Dyson P L, Devlin J C, Parkinson M L, et al. The Tasman International Geospace Environment Radar (TIGER): Current development and future plans[C]//2003 Proceedings of the International Conference on Radar. Piscataway: IEEE, 2003:282-287.

[7] Chen G, Zhao Z Y, Zhu G Q, et al. The Wuhan Ionospheric Sounding Systems[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4): 748-751.

[8] Shi S Z, Zhao Z Y, Su F F, et al. A low-power and small-size HF backscatter radar for ionospheric sensing[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 504-508.

[9] Chen G, Zhao Z, Zhang Y. Ionospheric doppler and echo phase measured by the wuhan ionospheric oblique backscattering sounding system[J]. Radio Science, 2007, 42(4): RS4007-1-13.

[10] Skolnik M I. 雷达手册[M]. 王军, 林强, 米慈中, 译. 北京:电子工业出版社, 2003: 5-20.Skolnik M I. Radar handbook[M]. WANG Jun, LIN Qiang, MI Ci-zhong, trans. Beijing: Electronic Industry Press, 2003: 5-20.

[11] Chen G, Zhao Z Y, Zhang Y N. Ionospheric Doppler and echo phase measured by the Wuhan ionospheric oblique backscattering sounding system[J]. Radio Science, 2007, 42(4):RS4007-1-13.

[12] Gonzalez R C, Woods R E. Digital image processing[M]. 3rd ed.New Jersey: Prentice Hall, 2008: 25-40.

[13] 戴耀森. 短波数字通信自适应选频技术[M]. 杭州: 浙江科学技术出版社, 1992: 10-30.DAI Yao-sen. Adaptive frequecy selection technology for short wave digital communication[M]. Hangzhou: Zhejiang Science and Technology Press, 1992: 10-30.

[14] Warrington E M, Stocker A J. Measurements of the Doppler and multipath spread of HF signals received over a path oriented along the midlatitude trough[J]. Radio Science, 2003, 38(5):1-1-12.

[15] Fitzgerald T J, Argo P E, Carlos R C. Equatorial spread effects on an HF path: Doppler spread, spatial coherence, and frequency coherence[J]. Radio Science, 1999, 34(1): 167-178.

[16] 王烽. 武汉电离层探测系统信号与数据处理分系统设计与实现[D]. 武汉: 武汉大学电子信息学院, 2009: 10-30.WANG Feng. Design and implement of signal and data processing subsystem in wuhan ionospheric sounding system[D].Wuhan: Wuhan University. School of Electronic and Information,2009: 10-30.