药事管理人才满意度调查分析

2011-07-30张友元长沙市医药中专学校教务办公室长沙410013中国药科大学国际商学院药事管理教研室南京10009

中国医院用药评价与分析 2011年9期

张友元，李伟(1.长沙市医药中专学校教务办公室，长沙 410013;.中国药科大学国际商学院药事管理教研室，南京 10009)

本文采用“实证调研+量化分析”的方法，在湖南省对与现有药事管理人才从事工作相关的部门、机构和社会公众等进行问卷调查。首先分别以卫生和药品监管部门、医疗机构、医药企业、药店等药品经营机构，高校等科研院所等为调查对象，选取样本数80份，对我国现有药事管理人才的满意度及其的影响因素进行调查;第二，影响医药行业对我国药事管理人才满意度的因素很多，主要有人才的知识结构、综合素质、创新意识、专业背景、英语水平、计算机水平、社会实践能力度、沟通能力、专业素养等，根据这些假设变量设计调查问卷，在问卷调查前对被调查者进行详细的解释;第三，回收问卷后，利用Excel 2007统计数据，对某些调查结果进行总体分析，同时将数据导入SPSS 18.0，对数据进行多元回归模型验证分析;最后，对统计结果进行讨论，分析确定影响我国现有药事管理人才的满意度最相关因素和各因素的影响权重，从而为完善和调整培养模式提供支持。

1 数据分析和模型验证

1.1 总体评价

本次实证调研共发放问卷80份，收集有效调查问卷53份，其中各部门机构的问卷来源情况见图1。

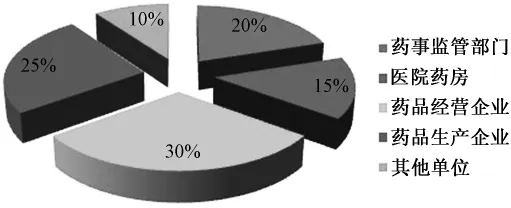
图1 问卷来源分布图Fig 1 Profile of sources of questionnaire

1.2 对药事管理人才满意度

对于本次问卷调查进行数据统计分析发现，样本对于我国现有药事管理人才的满意度呈现“两头小、中间大”的趋势，对现有药事管理人才的满意度集中在“一般”的水平，但是样本对现有药事管理人才的“满意”的水平只有9.43%，总体上对于现有药事管理人才满意程度一般，见图2。

1.3 对药事管理人才药学服务水平的评价

图2 对我国现有药事管理人才的满意度Fig 2 Satisfaction degree on current pharmaceutical management personnel

新医改要求:规范药品临床使用，发挥执业药师指导合理用药与药品质量管理方面的作用;完善执业药师制度，零售药店必须按规定配备执业药师为患者提供购药咨询和指导[1]。执业药师资格是药学服务人才的必备资质，是为了加强对药学技术人员的职业准入控制、确保药品质量、保证人们用药安全有效的重要制度。83.02%的被调查者认为药事管理人才应该具备执业药师资格，只要严格的资质准入才能保证良好的药学服务。样本对于“现有药事管理人才提供的药学服务水平评价”基本和“对人才的满意度”保持一致，总体上对于药事管理人才提供药学服务的水平评价一般，见图3。

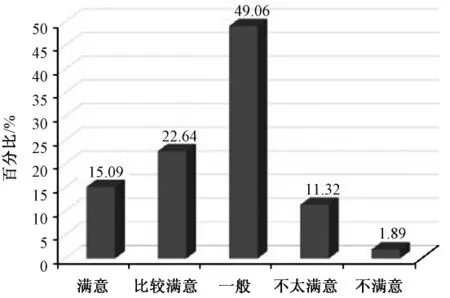
图3 对现有药事管理人才提供药学服务水平的评价Fig 3 Assessment on current pharmaceutical care level of pharmaceutical management personnel

2 多元线性回归模型验证

2.1 多元回归模型的定义

回归分析是研究一个变量关于另一些变量的依赖关系的计算方法和理论，其目的在于通过后者的已知或设定值，去估计或预测前者的均值。它是处理变量之间相关关系的一种数学统计方法，是最常用的数理统计方法，可以解决预测、控制、优化等问题，在工农业生产和科学研究及国民经济的各个领域均有广泛的应用。回归分析包括线性回归分析和非线性回归分析。非线性回归是回归函数关于未知参数具有非线性结构的回归，但某些非线性回归模型可化为线性回归模型处理[2]。在回归分析中，如果有2个或2个以上的自变量，就称为多元回归。多元线性回归模型的一般形式:Y=β0+β1X1+β2X2+β3X3+β4X4+μ(公式1)。

其中，影响Y的因素有X1，X2，…Xk，k个因素。Y为可观察的随机变量，称为因变量。X1，X2，…Xk为非随机的可精确观察的变量，称为自变量或因子，β0，…βk为k+1个未知参数，μ～N(0，σ2)为随机误差。为了估计未知参数β0，…βk及σ2，我们对Y与X1，X2…Xk同时作n次观察(试验)得n组观察值(Yt，Xt1，…Xtk)，t=1，2，…，n(n ＞ k+1)，它们满足关系式:yt=β0+β1Xt1+β2Xt2+… +βkXtk+εtt=1，2，…，n(公式2)。其中ε1，…，εn互不相关且均是与ε同分布的随机变量，我们称公式2为多元线性回归模型[3]。

2.2 影响因素的选取及赋值

本课题从微观角度对“我国现有药事管理人才的满意度(Y)”所选影响因素如下:综合素质(X1)、创新意识(X2)、药学专业背景(X3)、法学专业知识 (X4)、行政管理学知识(X5)、英语水平(X6)、计算机水平(X7)、社会实践能力(X8)、沟通能力(X9)。根据样本对现有药事管理人才满意度的不同对不同满意度赋值，赋值1为满意;2为比较满意;3为一般;4为不太满意;5为不满意。

2.3 模型的参数估计、检验及修正

利用SPSS 18.0软件对53例样本数据进行多元回归分析。

2.3.1 对回归模型的描述:回归模型对我国现有药事管理人才的满意度的预测效果较好，多重相关系数R=0.819接近于1(R表示的是拟合优度，它是用来衡量估计的模型对观测值的拟合程度，R值越接近1说明模型拟合度越高)，多重测定系数R2=0.670，多重测定系数的结果表明约有67.0%的满意度变化可以用模型解释，所以该模型拟合度较好，见表1。

表1 模型汇总Tab 1 Different models

2.3.2 对回归模型的方差分析:F值为9.720，sig值为0.000，显然sig＜0.05，说明因变量分别与自变量存在真实的线性关系，用全部自变量来预测对我国现有药事管理人才的满意度的多重回归模型与数据拟合程度比较好，显著性检验通过，见表2。

2.3.3 偏回归系数及检验:建立的多重回归方程中的常数、偏回归系数、标准化偏回归系数、对回归系数进行t检验的结果见表3。从中可以看到，预测的9个影响因素变量的显著性检验结果不显著(sig＞0.05)，说明这些变量之间可能存在多重共线性，也就是说它们对回归模型的作用有限。

2.3.4 多重共线性问题的解决以及回归模型修正:多重共线性对于多元回归模型的影响，主要在于高度相关的变量之间的相互影响使回归系数和回归平方和不再具有独立的意义，而是受到其他变量变化的影响[4]。但是方程的总的拟合能力不一定受多重共线性的影响，在多元回归方程中引入高度相关的变量，会使F检验值和决定系数值增大，造成方程拟合效果提升的假象。消除多重共线性的最有效的办法是删除共线性组中与因变量相关性最低的自变量，另一种有效的办法是采用逐步回归法[5]。这种方法优化回归方程的基本思路是:首先将变量一个个引入，引入的条件是系数的显著性符合检验标准;同时，每引入一个新变量后，要对原引入的变量逐个检验，把由于引入新变量后系数变为不显著的变量加以剔除，直到最后剩余的变量都不能引入及引入的量都不能剔除，这样得到的方程即为最优化的回归方程。利用SPSS 18.0对原数据进行逐步法多元回归分析，从而对回归方程进行优化，结果见表4、表5，通过“逐步法”对回归模型进行优化后，得出最终的回归分析模型:Y= －0.517+0.468X1+0.29X3+0.271X4+0.199X5。

表2 方差分析Tab 2 Analysis of variance

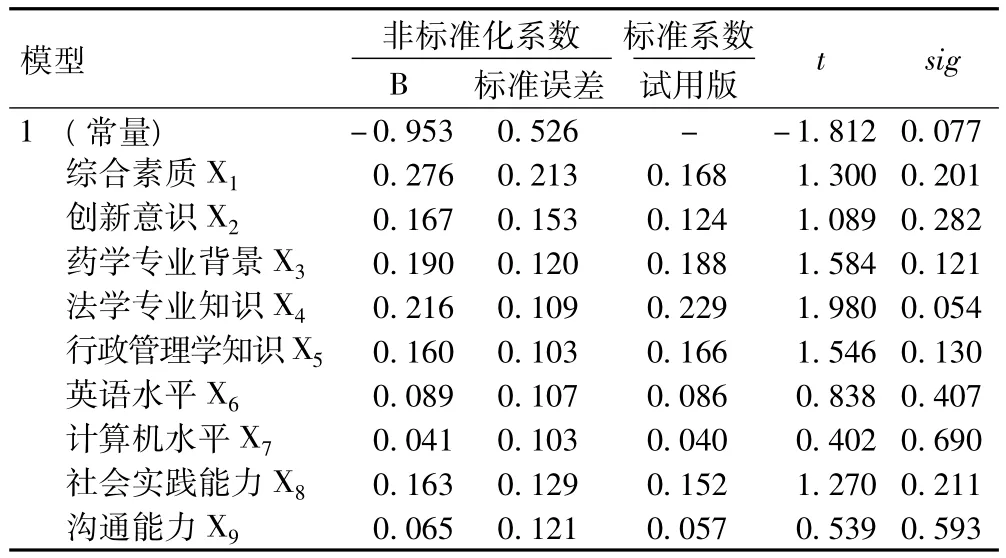
表3 系数aTab 3 Coefficienta

3 讨论

从回归模型上我们可以发现，根据课题组实证调查的53份数据显示，综合素质(X1)、药学专业背景(X3)、法学专业知识(X4)、行政管理学知识(X5)这4个因素是对我国现有药事管理人才满意度的重要影响因素，尤其是综合素质和药学专业背景。创新意识(X2)、英语水平(X6)、计算机水平(X7)、社会实践能力(X8)，沟通能力(X9)由于其sig值过大，因此被排除在模型之外，但是这并不代表这些因素对现有药事管理人才满意度没有影响，只是说明这些因素的影响作用比较小。根据多元回归模型分析的结果，课题组认为在今后的药事管理教学改革中，应该加大力度推进“素质教育”的培养模式，完善“以药学为依托、法学和行政管理学为主体、经济学为辅助”的学科体系，同时要加强双语教学、案例教学、第二课堂等教学方法的应用，努力提高学生的英语运用水平、沟通交流能力，这样才能培养出让社会满意的药事管理人才。