基于多视图几何的位置与遮挡一致性恢复方法研究
2011-07-29岩1何晓波涛2
张 岩1, 2,何晓波[1],管 涛2
基于多视图几何的位置与遮挡一致性恢复方法研究
张 岩,何晓波[1],管 涛
(1. 防灾科技学院,河北三河 065201;2. 华中科技大学数字化工程与仿真中心,湖北武汉 430074)
针对增强现实中的几何一致性问题,提出了一种基于多视图几何的虚实场景位置和遮挡一致性恢复策略,该方法利用计算机视觉中的多视图几何原理同时解决了增强现实系统中的位置配准和虚实遮挡两个重要问题,在保证系统实时性的前提下,最大限度增强了真实感以提高系统可用性。实验结果表明,该文方法是有效可行的,在完成位置配准的同时解决了虚实场景之间的遮挡问题,从而有效避免了不正确的遮挡关系给使用者造成的虚实场景相对位置失真的错觉。
计算机应用;几何一致性;多视图几何;位置与遮挡
增强现实(Augmented Reality, AR)是虚拟现实技术的一个重要分支,它借助显示技术、人机交互技术、多种传感技术和图形图像处理技术将计算机生成的虚拟场景、提示信息等叠加到使用者所观察到的周边真实场景中。AR的最终目的是使虚拟场景与真实环境融为一体, 使用户从感官效果上确信虚拟场景是周围真实场景的一部分。
1 研究背景
要做到虚实之间的无缝融合,几何一致性至关重要。具体说来主要有以下两点:位置一致性和遮挡一致性。位置一致性,或者称为虚实配准或三维注册,指的是虚拟场景在位置上应该与周边真实场景保持一致,它相对于真实世界的位置不应随用户视点和视角的变化而发生改变。遮挡一致性指的是虚拟场景与真实场景应该具备正确的遮挡关系,在遮挡背景的同时,虚拟场景应该能够被前景物体所遮挡。
当前研究较多的是位置一致性问题,国内外研究人员相继提出了一些解决方法。其中以计算机视觉为主要手段的虚实配准方法近年来已经成为一个重要的研究方向。增强现实领域的权威国际会议ISMAR(International Symposium on Mixed and Augmented Reality)以及IEEE的可视化与图形学学报(IEEE Transactions on Visualization and Computer Graphics)等重要期刊每年会都有相关最新研究成果发表。与位置一致性相比,人们对遮挡一致性所作的工作明显较少,主要方法是利用双目立体视觉装置来获取待注册场景的深度图,以恢复虚实场景之间的正确遮挡关系。然而,这种方法不论在精确性还是运行速度方面都无法达到令人满意的效果。
笔者在研究过程中发现,当前大多数工作都是将位置和遮挡作为两个相互独立的问题而展开研究,很少有系统能够同时兼顾并解决上述两种一致性问题。然而,对于一个实用的增强现实系统,遮挡一致性与位置一致性具有同等重要的地位。不正确的遮挡关系会给系统使用者造成一种虚拟场景与真实场景之间相对位置失真的错觉,很大程度上影响了系统的运行效果。为此,有必要将位置配准和虚实遮挡作为一个统一的问题加以解决。
近几年逐渐得到完善的计算机视觉中的多视图几何理论为我们解决几何一致性问题带来了契机。该理论为求解摄像机位姿和前景像素重投影提供了重要依据。本文的主要工作是设计了一种基于多视图几何原理的虚实场景位置和遮挡一致性恢复策略。该方法具有以下特点:
(1)以多视图几何为统一理论框架,在完成位置配准的同时有效解决了虚实场景之间的遮挡问题,一定程度上提高了系统的真实感。
(2)方法简单,除一个未定标摄像头和普通配置的PC机之外,无须任何其它硬件设备,也无须向场景中添加任何人为标识即可正常工作,具有较高的可用性。
(3)采用基于分类的全局与局部匹配相结合的特征点追踪策略,在提高宽基线约束下特征点匹配正确率与匹配效率的同时,使得系统能够在场景部分遮挡、视角发生大幅度变化的情况下,依然可以正常工作。
全文结构如下:第2节介绍了多视图几何基本原理,包括摄像机成像模型、对极几何和三焦距张量;第3节给出了系统的工作流程;第4节介绍了基于分类的特征点匹配策略;第5节分析了投影矩阵和三焦距张量的求解方法;第6节介绍了若干实现细节问题;第7节给出了实验结果;最后一节对全文作了总结。
2 多视图几何基本原理
2.1 摄像机成像模型
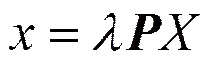
2.2 基本矩阵与三维重建
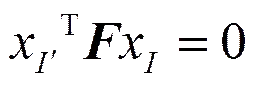
(3)
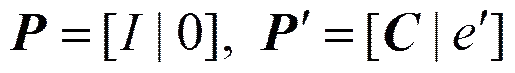
(5)


(8)
2.3 三焦距张量
三焦距张量在三视图中的作用类似于基本矩阵在两视图中起到的作用,它包含了三幅视图间不依赖于景物结构的所有影射关系。对于同一场景从不同视角拍摄的三幅图像,如果它们所对应的摄像机矩阵具有如下形式
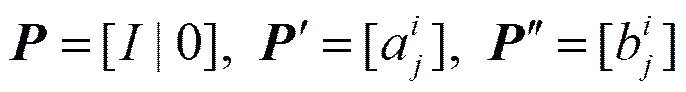
则三幅图像之间的三线性约束关系可以表示如下
(10)
如果已知真实世界中的一点在3幅图像中的2幅上的投影,则该点在第3 幅图像中的投影位置可由下式确定。

3 工作流程
算法的工作流程分为离线初始化和在线虚实合成两个阶段。
(1)离线初始化阶段,首先从不同角度获取目标场景的两幅图像作为参考,根据文献[12]中方法获取两者之间的特征点对应关系和基本矩阵,并利用2.2节方法对匹配特征点做重建,进而利用四点法建立世界坐标系。系统随后利用PCA和K-MEANS对匹配特征点集合作分类,以生成特征点描述符,供实时追踪过程使用。在对参考图像作校正之后,根据文献[14]中基于动态规划的全局优化方法获取两幅参考图像上前景区域像素间的对应关系。
(2)在线虚实合成阶段,首先将当前图像中提取到的特征点与离线阶段获取的特征点做匹配,根据特征点匹配集合计算透视投影矩阵以求取当前图像与两幅参考图像之间的三焦距张量。系统利用该张量完成前景像素和用户指定四点的重投影以恢复正确的虚实遮挡关系和计算三维注册矩阵。
4 基于分类的特征匹配
为了三焦距张量,必须首先获取当前图像与参考图像之间的特征点对应关系。由于固定在头盔式显示器上的摄像机所获取的图像与参考图像之间的基线距离会随使用者头部运动而发生较大变化,为此必须设计一种适合于长基线约束的特征匹配方法,它必须同时满足运算实时性和匹配精确性两方面的要求。本文采用文献[15]中提出的基于分类的方法来完成特征点匹配工作。该方法首先将参考图像上的特征点邻域作式(12)所示的仿射变换。以模拟系统运行过程中该特征点邻域在序列图像中的可能变化。
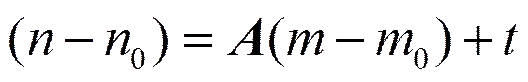
对于由仿射变换生成的邻域集合作主成分分析以达到降维和提取主成分的目的,随后利用K-MEANS对主成分集合作聚类分析以生成特征点描述符供后续匹配过程使用。实时匹配阶段系统将提取到的特征点邻域变换到主成分空间并利用最近邻法完成匹配。本文称上述方法称为全局匹配策略。笔者在实验过程中发现,基于分类的特征匹配方法对尺度、光照变化、旋转以及仿射变换都具有较强的鲁棒性。但它存在一个明显的缺点:为了确定当前图像上某一特征点的对应点,需要将该点与参考图像上每一个特征点作最近邻运算。上述过程非常耗时,是影响系统实时性的关键所在,有必要优化算法以进一步提高系统运行速度。由2.1节可知,真实世界中的特征点在当前图像上的位置完全可以由式(1)确定。受此启发,本文提出了一种基于透视投影矩阵引导的局部匹配策略来限定特征点的搜索范围以提高系统运行速度。该方法利用前一帧图像所对应的透视投影矩阵将通过三维重建获取的特征点投影到当前图像,以投影后的位置为中心构建局部搜索窗口,对位于窗口内的特征点执行与全局搜索策略相同的操作以确定特征点对应关系。实验证明,局部搜索策略在提高特征点匹配速度的同时,能够产生较全局搜索策略更多和更稳定的正确匹配数量。分析其原因是搜索范围的缩小不仅减少了最近邻运算的次数,而且能够有效减少描述符过于相近的点在搜索邻域内出现的概率。
实时注册阶段本文综合利用上述两种策略来完成特征匹配任务:初始化阶段(第一帧)采用全局匹配策略建立特征匹配集合,求取所需的透视投影矩阵。后续过程则采用局部匹配策略来完成特征点匹配。两种策略综合使用的好处有两点:
(1)系统正常运行情况下采用局部匹配策略完成特征点匹配操作,在保证匹配正确率的前提下能够满足系统的实时性要求。
(2)注册失败情况下,系统重新回到初始化状态执行全局搜索策略,以求取初始透视投影矩阵。这样做避免了人为初始化操作,一定程度上提高了系统的健壮性与可用性。
5 求取三焦距张量
为了完成虚实配准和前景像素重投影,必须首先获取当前图像与两幅参考图像之间的三焦距张量。当前较为常用的计算方法主要分为以下几种:线性或归一化线性算法、代数最小化算法和6点RANSAC算法。线性或归一化线性算法没有考虑到三焦距张量的内部约束,因而不能保证得到一个几何上有效的张量。代数最小化算法很容易受野值(误匹配特征点)影响,无法保证计算结果的精确性。6点RANSAC算法是当前较为常用的三焦距张量计算方法,该方法在避免野值影响的基础之上能够保证生成一个几何有效的张量。然而实验发现,RANSAC算法的运行速度很不稳定,其抽样次数随着对应点数量的增加以及误匹配率的升高而急剧增大。该方法的另一个缺点是,多平面环境下,如果选定的6点恰好位于一张平面上,则计算结果只能保证对该平面几何有效。
综合考虑上述方法各自的优缺点以及本文算法的特殊性,设计了一种新的张量求取方法。该方法在兼顾精确性的同时最大程度上保证了健壮性,从而使得系统能够在场景部分遮挡情况下依然正常工作。
由式(9)和式(10)可知,如果能够获取三幅图像对应的投影矩阵、、。则可以很容易的计算出系统所需的三焦距张量。由于离线阶段已经得到了两幅参考图像的投影矩阵(假定为和),在线阶段只需实时求取当前图像对应的投影矩阵(假定为)即可通过式(10)完成张量计算。
鉴于上述问题本文引入渐进式一致抽样算法——PROSAC来完成野值剔除任务。PROSAC与RANSAC的差异在于抽样集合不同,RANSAC从整个匹配点集合中随机抽样,而PROSAC则是从匹配度最高的子集中抽样,随着抽样次数的增加,子集的规模也越来越大,并最终达到全集,因此PROSAC的抽样结果与RANSAC是相同的,只不过改变了抽样结果的次序,使匹配度较高的特征点对较早被抽到,进而较早达到抽样终止条件以结束抽样。
本文在利用PROSAC计算投影矩阵时,首先将特征点集合按匹配度(特征点描述符间的欧式距离)作降序排列,生成有序集合=(1,2, …,),其中为相互匹配的特征点对数。鉴于计算一次最少需要6对对应点,所以初始抽样子集定义为6=(1,2,3,4,5,6),若从当前集合=(1,2,…,)中抽取任意6个不同元素的所有方法已经穷尽,则下一步抽样子集为+1=(1,2,…,,+1),且后续抽样结果由+1和从中随机抽取的5个样本组成。
基于PROSAC的投影矩阵计算方法可以归纳如下:
(1)利用PROSAC从匹配特征点集合中抽样,同时利用归一化线性算法计算的候选解。
(2)利用式(1)和上述候选解将通过重建获取的三维点投影到当前帧。根据投影点和实时提取到的特征点间的距离计算内点的数量。
文中判断内点的标准为投影点和实时提取到的特征点间的距离小于3个像素。
在获取了当前图像对应的投影矩阵之后,即可直接利用式(10)获取所需张量来完成前景像素重投影和虚实配准。然而,笔者通过实验发现,上述方法并不能取得令人满意的精确性,有必要采取措施来提高系统精度。
计算三焦距张量的另外一个途径是代数最小化算法,选择该算法的一个重要前提是已经在求取透视投影矩阵的过程中剔除了特征点匹配集合中的野值,因而无需重新进行野点剔除操作。由于三焦距张量具有27个未知数,算法中的最后一步是一个大型优化问题,非常耗时。为此作者省略了非线性最小二乘优化以提高系统实时性。实验结果表明上述省略所造成的负面影响可以忽略不计。图1给出了代数最小化算法的重投影误差曲线,可以看出代数最小化算法在大部分情况下能够保证较高的计算精度,对于其中的跳变,分析其原因是由于正确匹配的特征点数量过少所造成。这些跳变作用于系统的后果是前景区域像素重投影错位所造成虚实遮挡失真。为此有必要采取一定的措施来解决跳变问题。

图1 代数最小化算法重投影误差
事实上,上面介绍的两种张量计算方法具有一定的互补性,前一种方法的精确性较低,稳定性较好。后一种方法的精确性较好,但是存在跳变问题。可以通过综合使用上述两种方法来获取较为稳定的计算结果。即正常情况下采用代数最小化算法求取所需张量,发生跳变时则采用前一种求解策略来获取所需张量。改进后的方法的重投影误差如图2所示,可以看出改进方法较代数最小化方法在抑制跳变次数和幅度方面都有明显的效果。
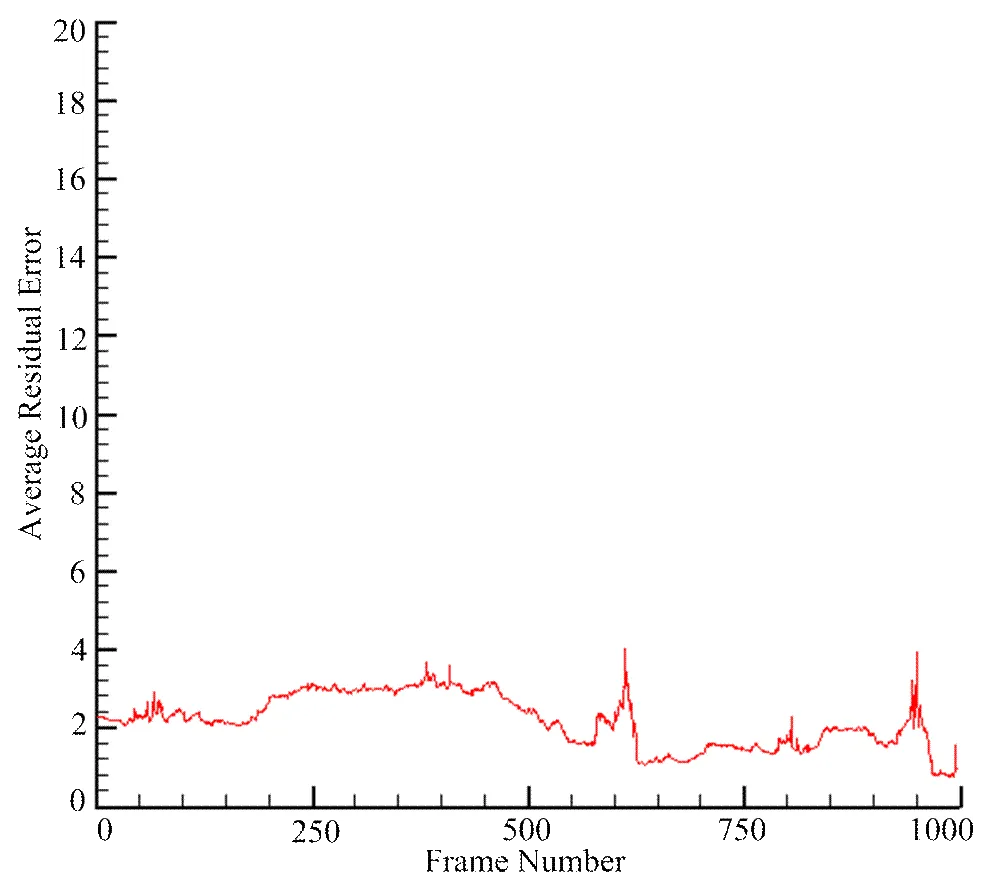
图2 改进算法的重投影误差
6 实现细节
本节介绍两个系统实现方面的细节问题:基于非线性最小二乘法的三维注册矩阵优化和前景区域空洞填补。
6.1 利用非线性最小二乘法优化三维注册矩阵
笔者通过实验发现,直接利用第5节获取的三焦距张量和ARTOOLKIT来完成虚实配准会造成虚拟场景位置抖动。为了进一步优化结果,本文利用式(13)对三维注册矩阵进一步求精,以提高系统稳定性。

6.2 前景区域空洞填补
利用三焦距张量将参考图像上的前景区域投影到当前图像上时会产生空洞现象。造成空洞的主要原因有两点:用户视角和视点变化引起的前景区域扩张以及离线阶段前景像素对应关系确定过程中产生的误差。空洞的出现使得用户可以从前景物体轮廓内部观察到应该被遮挡住的部分虚拟场景,很大程度上影响了虚实场景的合成效果。本文采用如下两种策略来克服空洞现象,以改善系统运行效果。
(1)区域填补,用参考图像上的前景像素覆盖以投影目标像素为中心的邻域。该邻域的大小与视点和前景的距离成反比。
(2)对于经过区域填补后存在的少量空洞,利用其周边像素色彩的平均值来填补。
7 实验结果
本小节从系统运行效果、注册精度以及算法运行时间三个方面给出详细的实验结果。实验的硬件平台为一台DELL 530图形工作站和一个普通USB摄像头。软件平台为Windows 2003、Visual C++ 6.0和Open CV。同时使用了文献[14]中提供的源代码来获取参考图像上的前景区域像素对应关系。
7.1 系统运行效果
图3、图4和图5给出了系统三次运行过程中的效果图,其中图3验证了系统在用户视角发生较大幅度变化、场景部分遮挡等情况下的工作性能,可以看出,本文算法在上述情况下仍然可以正常工作,因而具有较强的健壮性。
图4和图5就施加与未施加虚实遮挡的运行效果作了对比。其中,图4(a)、4(b)以及图5(a)、5(b)为没有施加遮挡的虚实合成效果,图4(c)、4(d)以及图5(c)、5(d)为本系统的运行效果。可以看出,没有施加遮挡功能的系统存在明显的不一致现象,很容易给使用者造成虚实场景相对位置失真的感觉。而本文方法很好的解决了上述问题,虚拟茶壶与杯子和糖果罐之间具备了正确的遮挡关系,使得虚实合成的结果更加具有真实感。
7.2 注册精度
为了验证算法的精确性,对注册精度做了定量分析,本文以三维注册矩阵中平移分量的(相对于摄像机坐标系轴的平移分量)为例分别对两次实验过程中的前100帧进行了计算,得出的计算结果与真实值之间的差异保持在5mm以内,可以满足系统的注册精度要求。
7.3 运行时间
记录了算法各主要步骤的运行时间,主要包括以下几个部分:
(1)全局与局部特征匹配;
(2)基于PROSAC的野值剔除;
(3)基于Levenberg-Marquardt的三维注册矩阵优化;
(4)计算三焦距张量;
(5)前景像素重投影。
全局特征匹配时间为0.195秒,局部特征匹配时间少于0.025秒。基于PROSAC的野值剔除时间少于0.01秒,基于Levenberg-Marquardt的三维注册矩阵优化需要0.015秒,计算三焦距张量需要0.014秒,前景重投影时间少于0.005秒。因此,系统初始化时间少于0.239秒,正常情况下,系统运行速度能够达到每秒14帧以上,可以满足实时性要求。

图3 系统运行效果一

(a) (b)
(c) (d)
图4 虚实遮挡效果对比一

(a) (b)
(c) (d)
图5 虚实遮挡效果对比二
8 总结和今后的工作方向
提出了一种基于多视图几何原理的虚实场景几何一致性恢复算法。该方法利用计算机视觉中的两视图和三视图几何原理同时解决了增强现实系统中的位置配准和虚实遮挡两个重要问题,在保证系统实时性的同时能够有效避免不正确的遮挡关系给用户造成的虚实场景相对位置失真的错觉,具有一定的参考和实用价值。当前存在的问题是待注册场景的结构在系统运行过程中不能发生变化,否则系统将无法完成位置配准和虚实遮挡。事实上真实场景的结构可能由于各种原因而发生改变(如物体被移动等),所以动态场景下的位置配准是当前增强现实领域中迫切需要解决的一个重要问题,基于张量选举的运动分割应该是一个很好的候选方案,这也是今后的工作方向。
[1] 施 琦, 王涌天, 陈 靖. 一种基于视沉的增强现实三维注册算法[J].中国图象图形学报, 2002, 7(7): 679-683.
[2] Kato H, Billinghurst M. Marker tracking and HMD calibration for a video-based augmented reality conferencing system [C]//IEEE and ACM International Workshop on Augmented Reality, 1999: 85-94.
[3] Simon G, Fitzgibbon A, Zisserman A. Markerless tracking using planar structures in the scene [C]//Proc. of International Symposium on Augmented Reality, 2000: 120-128.
[4] Simon G, Berger M. Reconstructing while registering: a novel approach for markerless augmented reality [C]// Proc. of the IEEE and ACM ISMAR, 2002: 285-294.
[5] Yuan M L, Ong S K, Nee A Y C. Registration based on projective reconstruction technique for augmented reality systems [J]. IEEE Trans. on Visualization and Computer Graphics, 2005, 11(3): 254-264.
[6] Raghav Subbarao, PeterMeer, Yakup Genc. A balanced approach to 3D tracking from image streams [C]//ISMAR, 2005: 70-78.
[7] Yuan M L, Ong S K, Nee A Y C. Registration using natural features for augmented reality systems [J]. IEEE Trans. on Visualization and Computer Graphics, 2006, 12(4): 569-580.
[8] Yokoya N, Takemura H, Okuma T, et al. Stereo vision based video see-through mixed reality[C]//Proc. of ISMAR, 1999: 131–145.
[9] Kim H, Yang S, Sohn K. 3D reconstruction of stereo images for interaction between real and virtual worlds [C]//Proceedings of the 2nd IEEE and ACM International Symposium on Mixed and Augmented Reality (ISMAR’03), 2003: 169-177.
[10] Hartley R, Zisserman A. Multiple view geometry in computer vision [M]. Cambridge University Press, 2000. 99-107.
[11] ARToolKit[EB/OL].http://www.hitl.washington. edu/artoolkit/, 2006.
[12] Zhang Z, Deriche R, et al. A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry [J]. Artificial Intelligence, 1995, 78(1-2): 87-119.
[13] Yuan M L, Ong S K, Nee A Y C. A generalized registration method for augmented reality systems [J]. Computers and Graphics, 2005, 29: 980-997.
[14] Scharstein D, Szeliski R. A taxonomy and evaluation of dense two-frame stereo comespondence algorithms [J]. IJCV, 2002, 47(1/2/3): 7-42.
[15] Lepetit V, Pilet J, Fua P. Point matching as a classification problem for fast and robust object pose estimation [C]//Conference on Computer Vision and Pattern Recognition, Washington, DC, 2004: 91-110.
[16] Chum O, Matas J. Matching with PROSAC- progressive sample consensus [C]//Proc. CVPR, 2005: 20-25.
[17] Wai-Shun Tong, Chi-Keung Tang, Gerard Medioni. Simultaneous two-view epipolar geometry estimation and motion segmentation by 4D tensor voting [C]//IEEE Transactions on Pattern Analysis and Machine Intelligence,2004: 1167-1184.
Resolving Pose and Occlusion Consistency Based on Multiple View Geometry for Augmented Reality Systems
ZHANG Yan, HE Xiao-bo, GUAN Tao
( 1. Institute of Disaster Prevention Science and Technology, Sanhe Hebei 065201, China; 2. Digital Engineering and Simulation Research Center, Huazhong University of Science and Technology, Wuhan Hubei 430074, China )
This paper proposes a novel method to solve pose and occlusion consistency problems by using multiple view geometry for AR systems. The method can deal with pose and occlusion consistencies simultaneously in an uniform framework, which improves the performance of AR systems obviously. Experiments have been carried out to demonstrate the validity of the proposed approach. The results indicate that the method can solve pose and occlusion consistencies problems, by which the wrong impression of relative position caused by incorrect occlusion can be avoided effectively.
computer application; geometrical consistency; multiple view geometry; pose and occlusion
TP 391
A
1003-0158(2011)01-0111-08
2009-04-01
国家自然科学基金青年基金资助项目(60903095);中国博士后基金面上资助项目(20080440941)
张 岩(1982-),男,北京人,硕士研究生,主要研究方向为图像处理,虚拟现实与增强现实技术。
