代数双曲Bézier曲线的扩展

张锦秀， 檀结庆



代数双曲Bézier曲线的扩展

张锦秀， 檀结庆

（合肥工业大学数学系，安徽合肥 230009）

提出了一类带多形状参数的双曲Bézier曲线（简称H-Bézier曲线），这类曲线与Bézier曲线类似，它不仅具有Bézier曲线许多常见的性质，而且利用形状参数的不同取值能够整体或局部调控曲线的形状。当形状参数增大时，曲线能连续逼近控制多边形。此外，它可以精确表示双曲线和悬链线。最后给出了曲线在连续下的拼接及在实物造型中的应用。

计算机应用；几何造型；双曲Bézier曲线；多形状参数；整体与局部调控

Bézier和NURBS模型是CAGD中曲线曲面设计和造型的基础，但是它们也有一些不足之处，如不能精确地表示很多非代数曲线，尤其是不能精确地表示工程设计中很常用的一些超越曲线，如双曲线、悬链线、指数曲线等。用于定义Bézier曲线和有理Bézier曲线的Bernstein基函数与定义B样条曲线和NURBS曲线的B样条基函数都是多项式空间上的函数。为此，人们试图在非多项式函数空间寻求解决问题的方法，相继出现了螺旋样条、张力样条、C曲线曲面等方法进行曲线曲面造型。文献[7-9]研究了代数双曲混合空间上类似于Bernstein基的代数双曲Bézier(H-Bézier)基，由这组基生成的代数双曲(H-Bézier)曲线具有许多类似Bézier曲线的性质，并且对相同的控制多边形，能够比Bézier曲线更好地保持曲线的形状，由于空间的特殊性，由这组基生成的H-Bézier曲线曲面可以精确表示一些由NURBS和C-Bézier基只能逼近表示的曲线曲面如双曲螺线、双曲抛物面等。因此，H-Bézier方法可以在曲线曲面建模和表示中得到很好的应用。

邬弘毅等在多项式空间提出带多个形状参数的Bézier曲线与曲面，它既能整体又能局部地调控曲线与曲面的形状，显然在多项式空间中，即使增加参数仍无法精确地表示圆锥曲线、双曲线或其他超越曲线，这只能在三角多项式空间、双曲多项式空间或混合空间中去解决，因此在这些空间中引入多个形状参数是件有意义的工作。本文在多项式与双曲多项式混合空间中构造了带多个形状参数的H-Bézier型曲线，既可以作整体又可以作局部调整，且当所有形状参数取值同为时，即为H-Bézier曲线，故称之为H-Bézier曲线的扩展。并以2次，3次等低次情况为例进行了详细讨论。

1 带多形状参数的H-Bézier基及其性质

定义 1 令初始函数

（1）

带多形状参数的H-Bézier基函数的性质：

结合定义1，运用数学归纳法可证明性质1，性质2，性质3。

性质 6 线性无关性

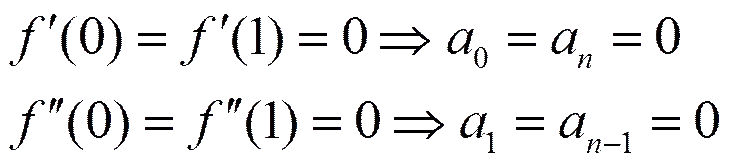
性质7 非负性

证明和H-Bézier基函数非负性证明相同，参见文献[7]。

其中

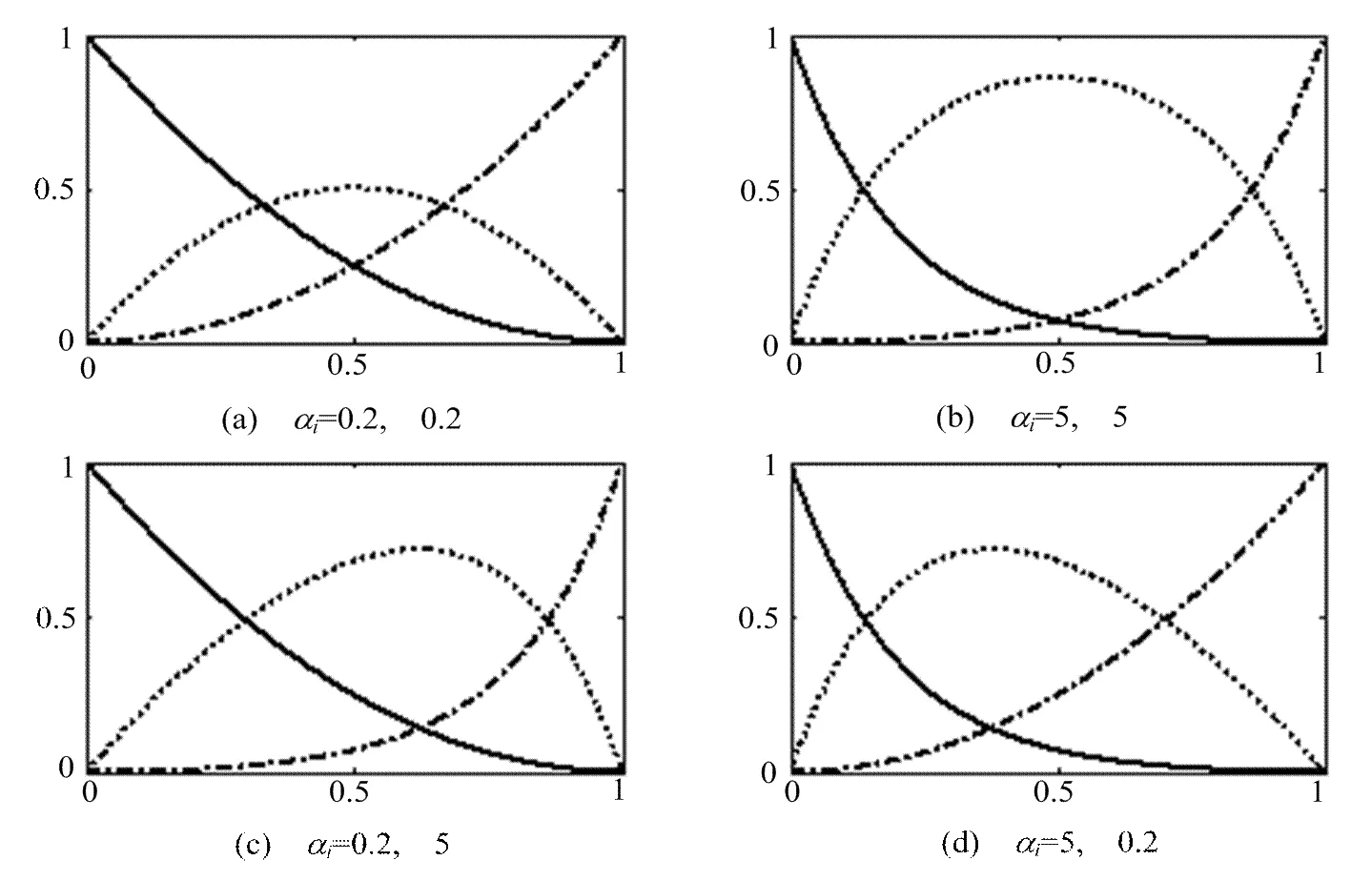
图1 n=2时的基函数

图2 n=3时的基函数

2 带多形状参数的H-Bézier曲线

定义 2 称

（4）

由基函数的正性和权性以及定义2可得。

性质10 几何不变性与仿射不变性：曲线仅依赖于控制顶点而与坐标系的选择无关；曲线作仿射变换只需其控制多边形作此仿射变换。

3 形状参数对曲线的影响

3.1 形状参数对二次H-Bézier曲线的影响

图3 a1, a2取不同值曲线的形状

3.2 形状参数对三次H-Bézier曲线的影响

图4给出了由四个控制顶点生成的单参数H-Bézier曲线由下到上取之分别为0.1, 2, 4, 8此图表明随着的增大曲线靠近控制多边形。但是，曲线的局部调控能力不强，不能做局部调整。

图4 单参数的H-Bézier曲线

图5给出了由4个控制点生成的多形状参数H-Bézier曲线。其中，各子图中实线表示单形状参数的H-Bézier曲线，取形状参数为。

图5 由4个控制点生成的多形状参数H-Bézier曲线

4 带多形状参数的H-Bézier曲线的拼接

与Bézier曲线类似，在设计复杂的自由曲线时，应采用分段技术，可以将带多形状参数的H-Bézier曲线段拼接成整条曲线。下面给出将带多形状参数的二次H-Bézier曲线段拼接成或连续曲线以及三次H-Bézier曲线段拼接成、或连续曲线的条件。

（1）带多形状参数的二次H-Bézier曲线段拼接

有

（5）

（2）带多形状参数的三次H-Bézier曲线段拼接

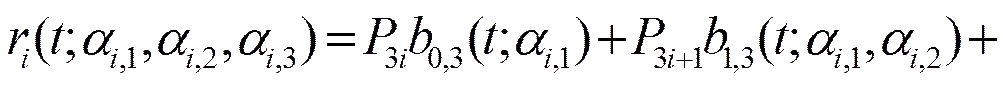
则有

（9）

（10）

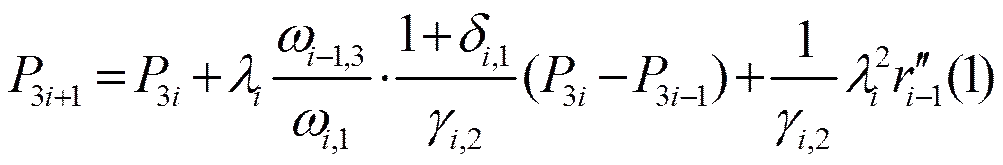
证 明 由式(9)，仿照定理1的证明可得。

5 带多形状参数的H-Bézier曲面

利用张量积可以定义一张带多形状参数的H-Bézier曲面，方程如下

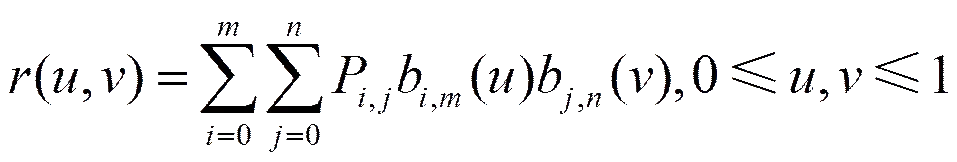
图6给出了带多形状参数的双三次H-Bézier曲面图。

图6(a)中所有形状参数均取为0.2。

图6(b)中所有形状参数均取为5。

图6(c)中两组基函数的形状参数均取为{5，0.2，0.2}。

图6(d)中两组基函数的形状参数均取为{0.2, 5, 0.2}。

6 图形实例

6.1 双曲线，悬链线的构造

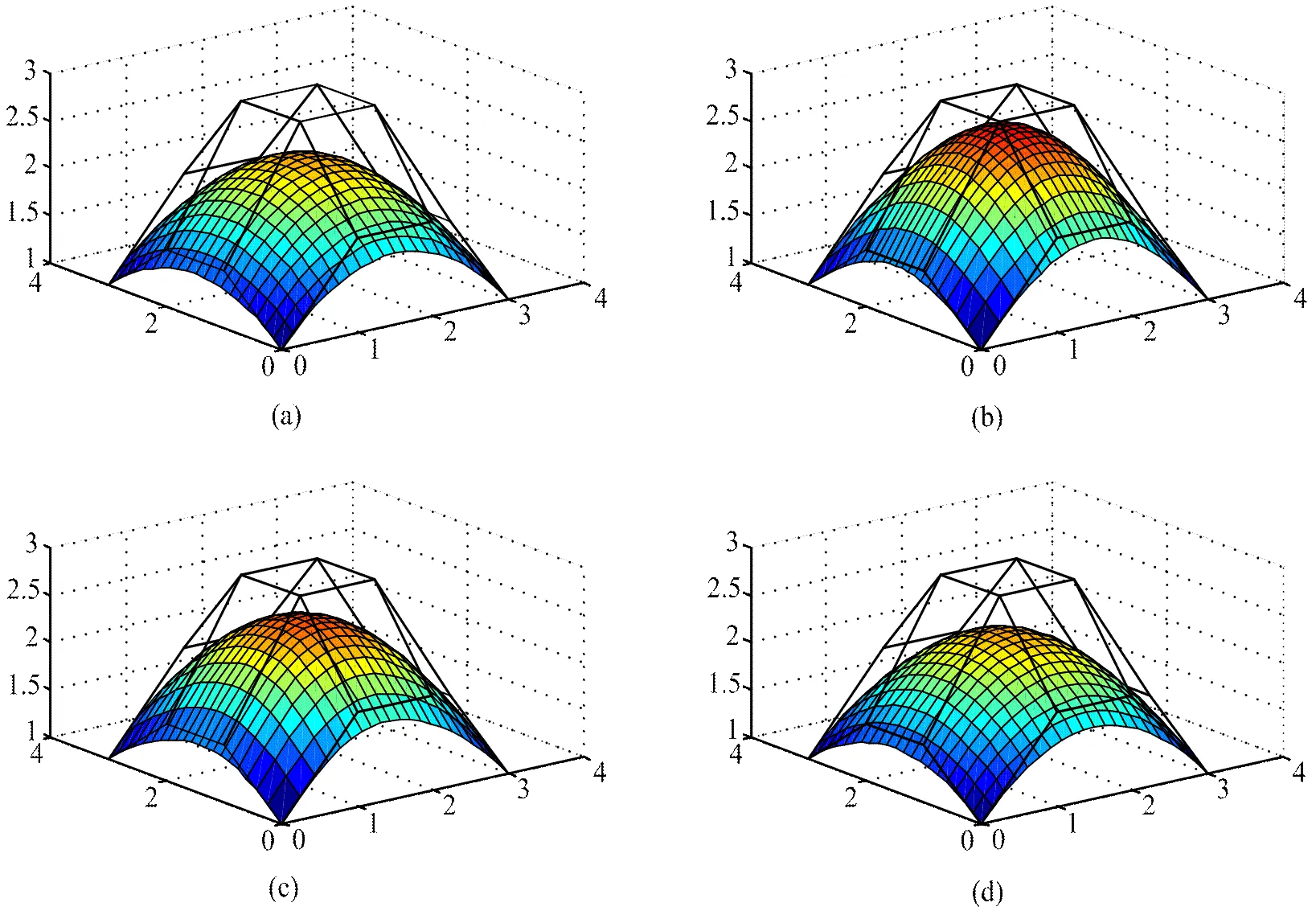
图6 带多形状参数的双三次H-Bézier曲面

图7 二次H-Bézier曲线精确表示双曲线

此外，三次H-Bézier还可以精确表示悬链线，如图8所示。

图8 三次H-Bézier曲线精确表示悬链线

6.2 花瓶绘制

通过曲线间的拼接技术，可以方便地把多形状参数的H-Bézier曲线应用到一些曲面造型中去。图9所示的是一个花瓶旋转曲面，其母线是由三条多形状参数的三次H-Bézier曲线拼接而成的，图9(a)为花瓶曲面的光照模型，图9(b)为花瓶旋转曲面的母线。其中第一段曲线形状参数，第二段曲线形状参数都取1，第三段曲线形状参数，通过修改形状参数的值相应的可以修改花瓶的形状。

(a) 花瓶的光照模型

(b) 花瓶的母线

图9 花瓶造型

7 结 论

本文在代数双曲混合空间中构造了带多形状参数的Bézier型曲线，既可以作整体又可作局部调整，且当所有的形状参数取值都为时，即为H-Bézier曲线。通过改变形状参数的值，使得H-Bézier 曲线具有更强的表现力，故能进一步补充应用于CAD/CAM曲线与曲面的造型中。

[1] 施法中. 计算机辅助几何设计与非均匀有理B样条[M].北京: 高等教育出版社, 2001. 306-343.

[2] Mainar E. Shape preserving alternatives to the rational Bézier model [J]. Computer Aided Geometric Design, 2001,18(1):37-60.

[3] Pottmann H. The geometry of tchebycheffian spline [J]. Computer Aided Geometric Design, 1993, 10(2): 181-210.

[4] Mazure M L. Chebyshev-bernstein bases [J]. Computer Aided Geometric Design, 1999, 16(7): 649-669.

[5] Zhang Jiwen. C-curves: an extension of cubic curves [J]. Computer Aided Geometric Design, 1996, 13(3): 199-217.

[6] Zhang Jiwen. C-Bèzier curves and surfaces [J]. Graphical Models and Image Processing, 1999, 61: 2-15.

[7] Li Yajuan, Wang Guozhao. Two kinds of B-basis of the algebraic hyperbolic space [J]. Journal of Zhejiang University Science, 2005, 6A(7): 750-759.

[8] Wang Guozhao, Yang Qinmin. Planar cubic hybrid hyperbolic polynomial curve and its shape classification [J]. Progress in Natural Science, 2004, 14(1): 41-46.

[9] 王 媛, 康宝生. 代数双曲混合H-Bézier函数及其性质[J]. 西北大学学报, 2006, 36(5): 693-697.

[10] 邬弘毅, 夏成林. 带多个形状参数的Bézier曲线曲面的扩展[J]. 计算机辅助设计与图形学学报, 2005, 17(12): 2607-2612.

Extensions of Hyperbolic Bézier Curves

ZHANG Jin-xiu, TAN Jie-qing

( Department of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China )

Hyperbolic Bézier curve (briefly H-Bézier curve) with multiple shape parameters is presented in this paper. The curve not only possesses most of the properties of the Bézier curve, but also can be adjusted totally or locally by taking the different values of shape parameters, with increasing of the shape parameters the curve can well approximate the control polygon. Moreover, the curve can represent hyperbolas and catenary exactly. At last, thecontinuous joint of curve pieces is discussed and some examples are provided to illustrate the application in geometric modeling.

computer application; geometric modeling; hyperbolic Bézier curve; multiple shape parameters; totally or locally adjust

TP 391.72

A

1003-0158(2011)01-0031-08

2009-06-01

国家自然科学基金资助项目（60773043；60473114）；教育部博士点基金资助项目（20070359014）；安徽省自然科学基金资助项目（070416273X）；安徽省教育厅科技创新团队基金资助项目（2005TD03）

张锦秀（1986-），女，安徽阜阳人，硕士研究生，主要研究方向为计算机辅助几何设计。