中点生成椭圆的整数型算法

张 博， 周丽韫， 李兴霞



中点生成椭圆的整数型算法

张 博， 周丽韫， 李兴霞

（佳木斯大学应用技术学院，黑龙江佳木斯154000）

在研究圆和椭圆生成算法基础上，通过构造递推表达式，给出中点生成椭圆的整数型算法，并对算法效率进行了分析。算法初始化时需进行两次乘法运算和一次移位运算，而生成各绘图点时只需要整数型加法运算，因此算法运算精度高、速度快，适合硬件的实现。采用VB编写程序对算法正确性进行了验证，该算法具有一定的理论和实用价值。

计算机应用；椭圆；整数算法；中点；Bresenham算法

对直线、圆和椭圆等生成算法的研究是近几年计算机图形领域的热点问题，关于圆和椭圆的生成算法较多，如Bresenham画圆算法，中点画圆法，椭圆双步增量生成算法，圆的高质量、快速生成算法等。可以看到椭圆的生成算法比圆的生成算法更加复杂，这些算法都采用构造方法，通过递推公式减少计算量，根据相应的判定条件，每次生成圆或椭圆上一个点的坐标，再调用画点函数在显示器上显示。算法的理论基础和构造技巧极为重要，以下对中点生成椭圆原理进行阐述。

1 椭圆的描述及区间划分

椭圆的方程为

其中为沿轴方向的长半轴长度，为沿轴方向短半轴长度。由于椭圆的对称性，研究椭圆的生成问题，只需研究第一象限的椭圆弧。

考虑第一象限椭圆左上部分，分量的变化小于分量；在右下部分，分量的变化大于分量。以弧上切线斜率为-1的点作为分界，把椭圆弧的划分为两个部分，假设该点坐标为(,)，该点的切线方程为

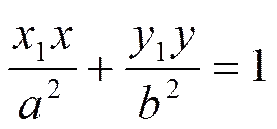
椭圆第一部分为0≤≤时生成的椭圆弧；第二部分为≤≤时生成的椭圆弧。把长半轴与短半轴互换，对应的椭圆方程为

椭圆第一部分为0≤≤时生成的椭圆弧的对应坐标，按横纵坐标对调可以生成以上方程 （1）第二部分的椭圆弧。

由此可见，对于以上两部分椭圆弧的生成，只需解决第一部分的椭圆弧的生成问题。

2 递推公式的构造

变换椭圆方程得

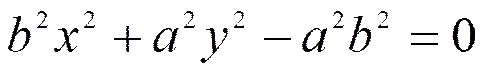
当(,)>0时，坐标点(,)在椭圆的外侧。

当(,)=0时，坐标点(,)在椭圆上。

当(,)<0时，坐标点(,)在椭圆的内侧。

0≤≤，每次递增量为1。

下面构造递推公式，根据已知的坐标点(,)，确定下一个要选取的坐标点，由(,)计算(+1,)和(+1,-1)。

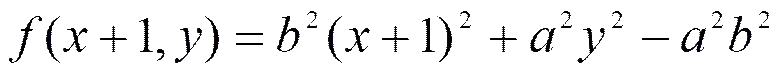
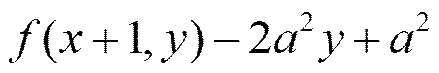
取和-1的中间点，计算(+1,-0.5)得

确定一个点后的值要加1，重复以上构造步骤，直到>时为止。

3 算法及说明

MidpointEllipse实现椭圆弧的绘制。为椭圆的两轴，为横坐标，为纵坐标。的每次增加量为1。While循环的结束条件为≤。

为前面构造的函数(,)随,的变化需要递加偏移量。

用来构造。

用来构造。

为中点判别式。

绘制第一象限的椭圆弧由两次调用完成：

MidpointEllipse( a, b, color );

MidpointEllipse( b, a, color );

其它三个象限可由对称性生成。

算法描述：

MidpointEllipse( a , b ,color )

int a, b, color;

{

int x, y;

long u, v, p, midcon, q, f, delt ;

x = 0; /*初始化*/

y = b;

p = 0;

u = a * a;

v = b * b;

midcon = Int( u / 4 ); /*可用移位运算代替*/

q = u * y;

While ( p <= q ) /*循环结束条件*/

{

If ( a > b ) /*a>b时，画线在椭圆的第一部分*/

{

drawpixel( x, y, color ); /*在坐标( x, y )位置color颜色画点*/

}

Else

{

drawpixel( y, x, color ); /*画线在椭圆的第二部分，坐标互换*/

}

f = f + p + p + v; /*计算x加1后，f和p的值*/

p = p + v;

x = x+1;

delt = f-q + midcon;

If ( delt > 0) /*delt>0取中点下面的点，否则取上面的点*/

{

f = f -q - q + u;

q = q – u;

y = y – 1;

}

} /*While结束*/

} /* MidpointEllipse*/

4 算法分析

以上算法执行两次调用，初始化需要一定时间，而算法的运行时间主要取决于While循环的次数。

由

解得

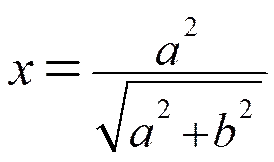
再把两个循环次数相加，可得中点生成椭圆整数型算法的时间复杂度为次加法运算。

5 中点生成椭圆的整数型算法的验证

见图1，用VB编写程序显示三个1/4圆周的椭圆弧（其中=4000,=2000），第一个是用“中点生成椭圆的整数算法”实现的，第二个是用常规直接计算法实现的（给定，根据椭圆方程计算点，再进行显示）。第三个图形是两种算法生成的图形共同显示，看一下图形重叠情况，用以验证算法的正确性。采用多组数据进行实际验证，第三个图形都重合的很好。

图1 椭圆生成算法验证

6 结束语

本文给出的算法已经编写程序上机进行了验证，生成的点平滑、连续性好。初始化后，算法采用整数加法运算，运算精度高、速度快，非常适合硬件的实现。中点生成椭圆的整数算法在递推公式的构造上有特点，算法具有一定的理论和实用价值。

[1] 刘勇奎. 直线与曲线的逐点生成算法[J]. 工程图学学报, 2005, 26(6): 41-50.

[2] 刘 凯, 侯伯亨, 吴成柯. 椭圆双步增量生成算法及其硬件实现[J]. 计算机辅助设计与图形学学报, 2003, 15(4): 18-21.

[3] 张 博. 圆的高质量、快速生成算法[J]. 计算机应用与软件, 1994, 11(2): 51-55.

[4] 谭浩强, 张基温, 唐永炎. C语言程序设计教程[M].北京: 高等教育出版社, 1999. 69-90.

[5] 严伟敏, 吴伟民. 数据结构[M]. 北京: 清华大学出版社, 1997. 21-26.

Integer Algorithm of Midpoint Generating Ellipse

ZHANG Bo, ZHOU Li-yun, LI Xing-xia

( College of Application Technology, Jiamusi University, Jiamusi Heilongjiang 154000, China )

Based on the research on circle and ellipse generating algorithm, integer algorithm of midpoint generating ellipse is presented by constructing recursion expressions, whose efficiency is also analysed. In initialization, the algorithm needs conduct multiplication twice and shift operation once, and every graphic point is calculated by integer addition, so the algorithm is fast and precise and can be realized by hardware. The correctness of the algorithm is tested by VB programming, and it is of theoretical and practical value.

computer application; ellipse; integer algorithm; midpoint; Bresenham algorithm

TP 391

A

1003-0158(2011)01-0001-04

2009-03-20

张 博（1966-），男，黑龙江伊春人，副教授，主要研究方向为计算机算法。