三角网格曲面纹理合成技术研究

王元龙1，张荣国1，冯军华1，刘 焜2



三角网格曲面纹理合成技术研究

王元龙，张荣国，冯军华，刘 焜

（1. 太原科技大学计算机科学与技术学院，山西太原 030024；2. 合肥工业大学机械与汽车工程学院，安徽合肥 230009）

纹理合成是真实感图形绘制中重要的技术。对由三角网格组成的曲面模型，提出了一种基于表面三角块矢量场的纹理合成方法。首先用矢量加平滑方法来计算曲面上每个三角块上的纹理方向矢量，并根据这些纹理方向来合成纹理；然后在样本纹理空间按扫描线顺序搜索样本纹理空间，找出最匹配的纹理坐标；算法用队列作为存取结构，并且结果保存在队列中，达到了实时绘制效果。实验结果与理论分析表明，算法纹理合成质量较高，运行结果较好。

计算机图形学；纹理合成；矢量平滑；三角网

在计算机图形学、虚拟现实等领域使用纹理来表现几何模型的细节，是一项最为常用的技术，它不仅提高了绘制的效率，而且降低了场景建模的复杂度。其中纹理映射和纹理合成就成为最近几年人们的一个研究热点。二者各有优点，其中也有很多研究人员把它们结合起来进行研究。

纹理映射作为应用于真实感图形绘制中的一项实用技术，首先是由Catmull在70年代中期提出的，称作Catmull算法，实现了参数曲面上的纹理映射。后来有很多改进算法，这些算法的基本目标是减少或避免映射中引起的接缝和扭曲。在1978年，Blinn提出利用扰动函数来生成凹凸效果的凹凸纹理映射技术，该技术增强了物体表面的真实感。1986年，Bier和Sloan提出了两步纹理映射技术，该技术取得了很好的效果。后来江等人提出了两步纹理的改进算法，显著提高了两步纹理映射的质量与真实感。最近几年人们对基于约束的纹理映射做了大量的研究，也是纹理映射的发展趋势，如Tang等人提出基于约束的纹理映，就是给纹理映射加了边界约束和斜率约束，来控制对象表面上特定的位置映射到纹理空间上的特定的纹理；Lee等人也提出了基于约束的纹理映射方法，这种方法是首先给出对象表面到纹理空间的一些约束点，然后通过边交换技术得到整个表面的纹理坐标。现在基于约束的纹理映射正越来越成为人们的研究热点。

纹理合成是为了解决小样本纹理映射到大的曲面上造成表面纹理的变形、扭曲以及模糊不清而提出的。它的基本思想是：给定一个有限的小样本纹理，生成任意大的样本纹理视觉上相似的纹理图像。早期的合成是基于样图的二维纹理合成，比较典型的有：①特征匹配的方法。如Heeger和Bergeg利用拉普拉斯和可控的金字塔进行的纹理合成；②基于马尔可夫随机场模型的纹理合成算法。如Wei和Levoy采用多分辨率模型进行匹配，提高了合成速度；③基于纹理块拼接的纹理合成。最有效果的是Wang Tiles方法，它能实时的合成纹理，并且适合于多种纹理合成。

最近10多年来，人们对曲面纹理合成也做了大量的研究。2001年SIGGRAPH会议上，Wei和Levoy提出了曲面纹理合成算法，Turk也提出了曲面纹理合成算法，他们虽然算法上有所不同，但都采用了多分辨率的思想，把二维纹理合成基于点匹配的思想拓展到了三维空间。受到二维纹理合成的块拼接思想和曲面最终可以转变成三角形块的启发，人们开始采用三角块纹理匹配的方法逐个合成网格中的每个三角形块，完成曲面纹理合成。汤等人提出用优先度方法从当前待合成三角块的相邻已合成三角块中提取纹理模版来合成当前待合成三角块算法，该算法用优先队列来控制优先度最高的三角块最先合成，并且用户可以控制纹理的方向和比例，所以合成效果很好，但对于三角块较多曲面速度较慢。吴等人提出了基于三角块的曲面纹理合成，它根据曲面切向量的方向，利用三角纹理块的方法直接在曲面上生成纹理，该方法提高了纹理的生成速度，但由于它不进行任何的预处理，对于曲面上少量的狭小三角形块效果仍不好。之后，薛等人对上述两种方法做了改进，它根据当前待合成三角块的相邻已合成三角块个数的不同，提出了基于纹理延伸和三角块拼接的曲面纹理合成，由于有一大部分三角块纹理是通过延伸得到的，所以该算法明显提高了合成的速度，但是它必须对输入的样本纹理做预处理生成可无缝自拼接的纹理，这就给算法增加了复杂度，且对结构性强的纹理效果也不是很好。

有些研究人员把纹理映射和纹理合成结合起来运用到曲面上，如江等人提出了局部纹理映射的纹理合成算法，它把曲面分成若干映射区和合成区，在映射区运用纹理映射方法，在合成区运用纹理合成的方法。它大幅度提高了曲面纹理合成的速度。

该文受到文献[10, 13]的启发，提出了一种实时曲面纹理合成的算法，运用队列存取控制曲面三角块，最后达到实时的纹理合成。和其它算法相比，优点在于：① 只要用户指定曲面上若干个三角块的纹理矢量方向（即整个曲面大致的纹理方向），就可以计算出曲面上每个三角块的纹理方向，这样可以按照用户预想的纹理方向合成纹理，提高可控性；② 该算法用队列作为存取结构，并且最终曲面信息都存放在队列中，这样当需要绘制曲面时，遍历整个队列就可以，达到了实时绘制的目的。

1 原理和方法

1.1 纹理矢量场的计算

大多数自然或人工纹理都有方向性，在曲面合成纹理时需要用户指定纹理方向，才能达到满意的效果。曲面纹理矢量场就是用来控制纹理在曲面上的大致走向。

曲面通常是由三角网格构成的，曲面矢量场是用曲面上每个三角形中心射出的矢量表示。计算矢量场：用户指定若干三角网格的矢量方向，然后用插值方法计算出剩下三角网格的矢量方向，最终生成一个平滑的矢量场，如图1所示。

图1 用户输入的矢量及插值生成的矢量场

1.2 纹理块尺寸的控制

纹理块的尺寸越大，纹理合成时间越短；反之，纹理合成时间就越长。但是，纹理块过大，块与块之间容易出现不连贯的情况；纹理块过小，可能会失去纹理的全局特征。所以纹理块选取的是否得当直接影响到合成结果。

此外，样本纹理中信息的变化是有一定周期性的，如果所选的纹理块尺寸对这个周期有比较好的反映，并且每个纹理块中的信息能比较好的反映出纹理的全局信息，那么这个所选的纹理块既可以反映出样本纹理的全局特性，又可以反映出样本纹理的局部特性。

1.3 搜索匹配

搜索匹配就是在样本纹理中搜索与已纹理化三角块匹配且和该三角块相邻的未纹理化的三角块的纹理坐标。这个过程是纹理合成中的关键步骤。

已纹理化三角块中的匹配区域用以约束纹理块的选取。如果匹配区域过窄，则在样本纹理空间中的候选块的个数就会增加，从而选到干扰块的概率就比较大，这将影响到纹理合成质量；如果匹配区域过宽，那么计算量就会增大，这就影响到了搜索的速度，从而大大增加了纹理的合成时间。因此，要选择合适宽度的匹配区域，使其既保证合成质量，又有较快的合成速度。

大部分计算匹配区域的误差距离为

=S{(R-R)+(G-G)+(B+B)}或

=S{(R-R)^2+(G-G)^2+(B+B)^2}

其中,,是颜色的三个分量，下标和分别表示已纹理化三角块的匹配区域和当前待合成三角块在样本纹理空间中的匹配区域。

2 曲面纹理合成

曲面纹理合成的目的是根据一定的算法遍历曲面网格上的每个三角块，计算其在样本纹理空间中的纹理坐标，并保证这些三角片纹理的连续性。而曲面上每个三角块的法向量不平行，这给计算曲面纹理矢量场带来了很大的困难，该文提出了一种计算曲面矢量场的方法。

2.1 相关的知识

（1）计算两个矢量的夹角

设矢量={,,},={,,},和的夹角是。那么

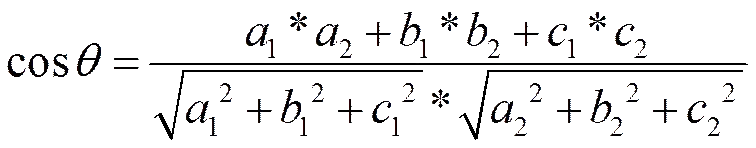
（2）旋转三角形

把一个三角形绕任意轴旋转一定的角度且旋转后三角形的大小形状都不变，设一个任意轴，点的坐标为(,,),的方向矢量为{,,}, 则一个三角形绕旋转角度所对应的就是三角形3个顶点分别乘上矩阵，而为

2.2 曲面纹理矢量场的计算

首先旋转曲面上的每个三角形使三角形3个顶点的轴坐标相同（间接的确认每个三角形在同一个平面上），设任意三角形的3个顶点的坐标分别是(,,)，(,,)，(,,)，三角形的法向为={,,}。作者的方法分两步进行。

第一步，把点、绕过点并且平行于面的矢量旋转（该矢量在三角形面上），使该三角形的法向量和面平行。旋转矩阵为

第二步，把点、绕过点且平行于轴的矢量旋转，使三角形的法向量平行于轴正方向。旋转矩阵为

曲面上的每个三角块被旋转后法向量都平行于轴，这样可以把旋转后的三角块看成是在同一个平面上，这样就容易计算矢量场了。

作者用个矢量的平均矢量等于这个矢量的和，最后把它单位化，来计算除用户指定外曲面三角网格的矢量方向，最终生成一个平滑的矢量场。此方法编程简单，易用，且速度快，如图2所示。

图2 矢量加来计算平均矢量

2.3 搜索匹配的过程

该文用到的搜索方法是从已纹理化的纹理三角块中提取模版（也就是匹配区域），根据当前待纹理化三角块的纹理方向矢量，在样本纹理中按扫描线的顺序搜索，找到与提取模版纹理值最相近的纹理坐标作为当前待纹理化三角块的纹理坐标值。

从已纹理三角块中提取匹配模版，该文取所在边长的1/5，如图3所示（阴影部分是所提取的匹配模版。

图3 匹配模版

图4是一个待合成三角块根据纹理方向旋转且按纹理块尺寸缩放得到的，曲面上的每个三角块都用此方法来确定三角块提取模版在样本纹理空间中的初始位置。

图4 纹理方向旋转且按纹理块尺寸缩放

然后，把已合成三角块相邻的当前待合成的三角块按照上述的方向旋转放到纹理空间底部，并同样提取出匹配模版（紧贴相邻已纹理化三角块），接着按一定的步长用扫描线的方法顺序搜索样本纹理空间，找出和已纹理化三角块的模版最相近的纹理坐标赋给当前待合成三角块，如图5所示。

图5 搜索过程

3 算法的具体步骤

根据模型表面三角块的蔬密程度来控制纹理合成块的大小，同时用户也能控制纹理合成块的大小。首先，在纹理合成前计算每个三角块中的最长边，用最长边来控制各个三角块纹理的大小。然后设置一个用户能控制的参数ratio乘到这个最长边上，这样用户就可以控制要合成模型表面的整体纹理了。具体步骤如下：

Step 1 根据用户指定三角块的纹理方向矢量，计算出曲面上每个三角块的纹理方向矢量。

Step 2 从曲面中随机地选取一个种子三角块，把它放入队列中，其中包括该三角块的顶点信息和已计算出的纹理矢量方向信息。根据纹理矢量方向信息随机给种子三角块赋纹理坐标。

Step 3 从队列头部获取一个三角块，根据所得三角块的纹理坐标，从样本纹理中分别搜索和此三角块匹配的相邻未合成的三角块的纹理坐标，并把它们放入队列中。

Step 4 融合边界区域，回到Step 3，直到遍历完整个曲面的每个三角块。

Step5 纹理曲面的绘制。

曲面上三角块信息（包括顶点坐标和纹理坐标）都存放在一个队列中了，当需要绘制地形时，只要遍历整个队列提取出每个三角形的信息进行绘制就可以了，达到了实时绘制。作者用到的三角形每个顶点的结构如下：

typedef struct TexturePoint

{

float x, y, z; //点的坐标

float u,v; //纹理的坐标

float psx,psy,psz; //点的方向矢量

}TexturePoint;

每个三角形由三个点（TexturePoint）构成，

typedef struct queue

{

TexturePoint point1;

TexturePoint point2;

TexturePoint point3;

struct queue * next;

}queue

存放在队列中的三角形结点。

4 实验及结果分析

在Windows XP系统下，使用OpenGL图形开发包工具和VC++6.0编绎环境进行实验，实验结果如图6所示。

这里图6(a1)和图6(c1)样本纹理图用.RGB格式和图6(b1)用.jpg格式，原纹理样图大小都是128*128像素。地形曲面由32个三角块组成，球体曲面都是由768个三角块组成，由图6可以看出，该文算法合成质量较高。表1给出了实验数据。

从表1中的数据可以看出，该文算法绘制时间较短，比较适合实时的绘制。为了进一步说明该文的合成效率，基于相同的三角网格数，作者给出了该文算法和文献[12]算法的合成时间对比，如表2所示。

与传统算法相比，由于该文不需要进行样本纹理的预处理，所以比文献[12]节省了时间。实验数据表明，对于一般的网格模型，该文算法的合成时间约为文献[12]算法的1/3，并且该文用队列存储了纹理坐标，所以显示是实时的。

该文算法主要是在搜索匹配的过程中花费了一些时间，需要曲面上的每个三角块都搜索一遍样本纹理空间，但这个过程是在预处理函数中进行的，预处理之后曲面上各顶点的信息都放到队列中了，当需要绘制时只要遍历队列就行，所以这不影响模型绘制的实时性。

图6 该文算法合成

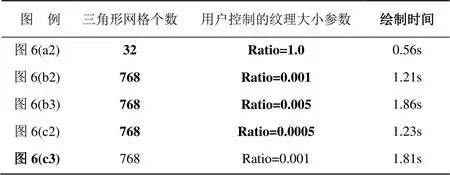
表1 合成纹理实验数据

表2 该文算法和文献[12]算法时间对比

5 结束语

该文提出了一种实时曲面的纹理合成的算法。实现用户控制纹理方向实时的纹理合成。研究主要针对虚拟现实中随视点的改变地形需要实时的绘制来进行的，接下来就是把它应用到虚拟现实中。如果曲面不够光滑（也就是相邻三角块间的夹角太大），那么相邻三角块间的纹理也就不太光滑。此时就需要对曲面进行细分预处理，文献[15]是三角网格细分的一种方法。这也成为将来工作的重点之一。

[1] 彭群生, 鲍虎军, 金小刚. 计算机真实感图形的算法基础[M]. 北京: 科学出版社, 1999. 235-291.

[2] 江巨浪, 张佑生, 等. 两步纹理映射的改进[J]. 系统仿真学报, 2006, 18(5): 1157-1160.

[3] Tang Ying, Wang Jin, Bao Hujun, et al. RBF-based constrained texture mapping [J]. Computer Graphics, 2003, 27(3): 415-422.

[4] Lee Tong-Yee, Yen Shao-Wei, Yeh I-Cheng. Texture mapping with hard constraints using warping scheme [J]. IEEE Transactions on Visualization and Graphics, 2008, 41(2): 382-395.

[5] Heeger David J, James R Bergen. Pyramid based texture anlysis/synthesis [C]//Computer Graphics Proceedings, Annual Conference Series (SIGGRAPH 95), 1995: 229-238.

[6] Wei Livi, Levey Marc. Fast texture synthesis using tree-structured vector quantization [C]//Proceedings of SIGGRAPH 2000, 2000: 179-488.

[7] 王 栋, 王去峰, 常宁宁. 纹理合成典型算法及分类比较[C]//科技信息(高校讲坛), 2008: 166-166.

[8] Wei Liyi, Levoy Marc. Texture synthesis over arbitrary manifold surfaces [C]//Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH, Los Angeles, California, 2001: 355-360.

[9] Turk G. Texture synthesis on surfaces [C]//Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH, Los Angles, 2001: 347-354.

[10] 汤颖, 孙汉秋, 张宏鑫, 等. 用户控制的纹理合成[J]. 计算机辅助设计与图形学学报, 2004, 16 (10): 1412-1418.

[11] 吴福礼, 石教英. 基于三角块的曲面纹理合成[J].计算机辅助设计与图形学学报, 2005, 17(2): 236-242.

[12] 薛 峰, 张佑生, 江巨浪, 等. 基于纹理延伸和三角块拼接的快速曲面纹理合成[J]. 计算机辅助设计与图形学学报, 2007, 19(2): 221-226.

[13] 江巨浪, 张佑生, 等. 运用局部纹理映射加速曲面纹理合成[J]. 计算机辅助设计与图形学学报, 2008, 20(11): 1507-1513.

[14] 聂俊岚, 王艳芬. 块纹理合成中纹理块尺寸自适应算法[J]. 计算机辅助设计与图形学学报, 2008, 20(10): 1353-1357.

[15] 王艳艳, 张荣国, 王 蓉, 等. 向量线性相关的三角网格自适应Loop细分方法[J]. 工程图学学报, 2009, 30(1): 91-96.

Study on the Texture Synthesis of Triangular Mesh Surfaces

WANG Yuan-long, ZHANG Rong-guo, FENG Jun-hua, LIU Kun

( 1. School of Computer Science and Technology, Taiyuan University of Science and Technology, Taiyuan Shanxi 030024, China;2. School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei Anhui 230009, China )

Texture synthesis is an important technology in a realistic figure rendering. A texture synthesis method is presented which is based on surface triangular mesh vector field for surface model consisting of the triangular mesh. First, the texture vector direction of each triangle of surface is calculated by using the vector sum method, and the texture vector direction is used to synthesize surfaces texture. Second, the best match of the texture coordinates is found in the sample texture space by scanning line sequence. The algorithm uses a queue as the structure of depositing and withdrawing, and the results are stored in the queue to achieve real-time rendering. Some experimental results and theoretical analysis show that texture synthesis quality of algorithm is higher and running results are better.

computer graphics; texture synthesis; vector smooth; triangular mesh

TP 391

A

1003-0158(2011)01-0104-07

2009-06-30

国家自然科学基金资助项目（50775060）；山西省教育厅资助项目（20081086）

王元龙（1983-），男，山西大同人，硕士，主要研究方向为计算机图形图像处理。