基于Monte Carlo模拟的非参数多重比较方法评价

滨州医学院(264003) 孙红卫 王 玖 韩春蕾

在实际工作中，经常要用Kruskal-Wallis检验对多于2组的数据进行比较，如果有统计学意义，需要采用非参数的多重比较方法(multiple comparison procedures，MCP)来鉴别到底哪两组有差异。相比参数检验的MCP，非参数MCP研究较少，提供的方法不多，且统计软件没有直接调用的过程可供实现。本文收集了在实际中常常采用的5种非参数MCP，用Monte-Carlo模拟来考察这些方法的第一、二类错误和判对率，并对实际中应用MCP提出建议。

非参数多重比较方法

1.Dunn_z

这是Dunn〔1〕在1964年提出的一种用于非参数多重比较的方法。第i组和第j组进行比较的统计量为:

z服从正态分布。要对检验水准进行调整，α'=2α/k(k-1)，z与za'比较。为两对比组中第i组、第 j组的平均秩和;ni、nj为 i组、j组的样本含量;N为总例数。

2.扩展的t检验法

扩展的t检验法是卫生统计学第6版教材〔2〕中介绍的方法。第i组和第j组进行比较的统计量为:

t服从自由度为N-k的t分布。其中，Ri、Rj、ni、nj、N的意义同上，k为组数，H为Kruskal-Wallis检验所得的统计量。这种方法也需要编程实现。

3.秩次转换之后的LSD(R_LSD)、SNK(R_SNK)和Bonferroni(R_BON)

Conover和 Iman〔3〕认为，对于非参数多重比较的问题，可以对数据取秩次之后，再对秩次用参数多重比较的方法来解决。这也是实际工作中经常采用的方法。本文考察了R_LSD，R_SNK和R_BON三种方法的性能。

在以上五种方法中，经过证明，R_LSD与扩展的t检验法是等价的。所以，本文主要考察了四种非参数多重比较方法，即Dunn_z，R_LSD，R_SNK和R_BON。

评价指标

理想的多重比较方法不但控制第一类错误在一定的检验水准下，而且能够尽量减少第二类错误，提高检验效能。

1.第一类错误〔4〕

(1)CER(comparisonwise error rate)，指在单个的假设检验中犯第一类错误的概率大小

(2)FWE(familywise error rate)，为实验的第一类错误。在检验集合的所有假设检验中出现第一类错误的概率，即检验集合中至少发生了一个CER错误的概率。这是多重比较方法需要控制的指标。

2.第二类错误〔5〕

(1)CP(complete power)，即完全效能，指在检验集合的比较中发现所有的差异的能力。

(2)PP(proportional power)，即比例效能，指在一次两两比较中发现差异的能力。

3.TM(true model)〔6〕

判对率指对于检验集合的统计推断完全正确的概率，其同时考察了犯第一、二类错误的概率。

模拟实验设计

由于非参数多重比较主要用于不满足参数检验的条件时，比如不符从正态分布，或者虽然正态分布但是方差不齐时，所以考虑了两种分布，一是对数正态分布，二是正态分布但是方差不齐。

考虑到多重比较方法的性能受到多个因素的影响，比如样本含量、组数等，还有就是均数间的差异、方差大小等。为了尽量模拟实际应用情况，实验设计见表1、表2。

表1 正态分布方差不齐时的实验参数设定

表2 对数正态分布时的实验参数设定

在不同组合下根据对应的分布产生随机数，并用4种多重比较方法进行检验，考察4种方法的一类错误，二类错误以及判对率。随机数的产生在SAS8.2上实现，4种多重比较方法及各种指标的计算均利用SAS的宏功能。每种组合下均模拟1000次。结果的分析使用SAS8.2和SPSS13.0实现。

结 果

本文两种分布皆考虑了总体均数全部相等，总体均数部分相等和总体均数全部不等三种情况。经过分析发现，正态分布方差不齐和对数正态分布的结果相似，所以两种分布的结果合在一起分析。

1.总体均数全部相等

由于所有总体均数全部相等，不可能犯第二类错误。这里要考察的指标只有FWE。

从表3可以看出，Dunn_z和R_BON对FWE的控制在0.1以下，而R_SNK的FWE超过了0.1的部分占17.4%，且当样本量小于20时，其检验水准都控制在0.1以内。而R_LSD的FWE失去了控制。

表3 总体均数全部相等时FWE的模拟结果

2.总体均数部分相等

由于总体均数部分相等，这里要考察的指标有FWE，CP，PP及 TM(结果见表4～6，图1～4)。

表4 总体均数部分相等时FWE的模拟结果

表4和表3的结果相近，但是在部分相等时，四种方法的FWE都减小了。其中Dunn_z控制在FWE在0.1以下，而R_BON超过0.1的部分只有2.8%，R_SNK超过0.1的部分有23.5%，但当样本量小于20时，其FWE超过0.1的部分只有7.4%，而这时R_LSD的FWE超过0.1的部分有19.8%。

从图1可以看出，Dunn_z法FWE中位数随样本量的增长变化不大，R_BON次之，而R_SNK和R_LSD增长较大。

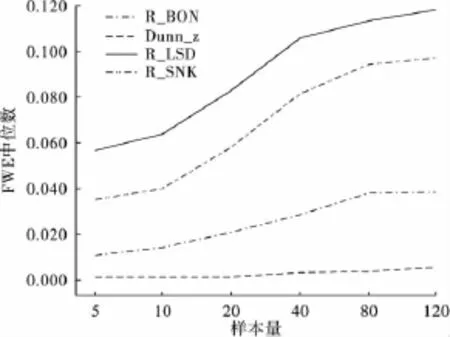
图1 总体均数部分相等时FWE的中位数随样本量的变化情况

图2 总体均数部分相等时FWE的中位数随组数的变化情况

从图2可以看出，Dunn_z和R_BON的FWE在组数增大时变化不大，这由于两种方法都根据组数来调整了检验水准。R_SNK的FWE变化不大，而R_LSD的FWE随组数的增长而增大。

表5 总体均数部分相等时CP和PP的模拟结果

从表5可以看出，R_LSD和R_SNK的完全效能和比例效能接近，都较高，R_BON次之，Dunn_z的检验效能最低。

从图3可以看出，四种方法的检验效能都随着样本量的增长而增大，且之间的差距越来越小。当样本量大于40时，四种方法的检验效能相近。

图4显示四种方法的完全效能都随着组数的增长而减小，但是减小的程度不一样，Dunn_z的完全效能下降幅度最大 ，R_BON的下降幅度也较大，而R_SNK和R_LSD的完全效能下降幅度较小。

图3 总体均数部分相等时CP的中位数随样本量的变化情况

图4 总体均数部分相等时CP的中位数随组数的变化情况

表6 总体均数部分相等时TM的模拟结果

判对率综合了第一类错误和第二类错误，从判对率的角度看，其中最高的是R_BON和R_SNK。

3.总体均数全部不等

由于所有总体均数全部不等，不可能犯第一类错误。这里要考察的指标只有CP和PP。

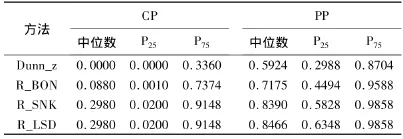
表7 总体均数全部不等时CP和PP的模拟结果

R_LSD和R_SNK的完全效能和比例效能接近，都较高，R_BON次之，Dunn_z最低。

结 论

选择合适的检验方法的原则是能将FWE控制在一定的水准下，选择检验效能最高的方法。

从上面的结果中可以看出，R_LSD、R_SNK、R_BON以及Dunn_z犯第一类错误的概率依次减小，但检验效能也依次减小。

R_LSD以控制CER为目的，所以它的FWE不受控制，会远大于检验水准，而R_SNK在样本量比较小时，基本控制在0.1内。而两者的检验效能相差不大。所以综合来看，R_SNK要优于R_LSD。

R_BON与Dunn_z都将FWE控制在0.1内，但是R_BON的检验效能要比Dunn_z高出很多，所以，在两者中R_BON较优。

R_BON与R_SNK比较，R_BON控制FWE的能力较高，但是检验效能较低。从前面的结果可以看到，R_BON的FWE随组数和样本量变化比较平稳，但是检验效能却随着组数的增大和样本量的减小而减小，在组数较小或样本量很大时，其检验效能与R_SNK接近。所以当组数较小时，可以选用R_BON，而在组数较大时，如果样本量也较大，可以考虑用R_BON，而如果组数较大但样本量不大时用R_BON，检验效能会较低。这时可以考虑用R_SNK，其检验效能较高，而在样本量较小时，其FWE基本控制在0.1以内。

综上，五种方法的性能如下:扩展的t检验法与R_LSD 等价，R_LSD、R_SNK、R_BON 以及 Dunn_z犯第一类错误的概率依次减小，但检验效能也依次减小。四种方法受样本量和组数的影响不同。R_BON和R_SNK是两种较优的方法。在实际中，当组数较小时，或组数较大，且样本量也较大时，可以选用R_BON;而如果组数较大，样本量较小时，可以选用用R_SNK。

1.Dunn O.Multiple comparisons using rank sums.Technometrics，1964，6:241-252.

2.方积乾主编.卫生统计学.第6版.北京:人民卫生出版社，2008:183-187.

3.Conover W，Ronald L.Rank Transformations as a Bridge Between Parametric and Nonparametric Statistics.The American Statistician，1981，35(3):124-129.

4.Westfall P.Multiple comparisons and multiple tests:using the SAS system.Cary，NC:SAS Institute，Inc，1999:16-21.

5.Seaman M.New developments in pairwise multiple comparisons:Some powerful and practicable procedures.Psychological Bulletin，1991，110(3):577-586.

6.Cribbie R.Pairwise multiple comparisons:A model comparison approach versus stepwise procedures.British Journal of Mathematical and Statistical Psychology，2003，55:27-39.