中国机动车辆保险核保系统构建的实证研究

冷 军，周新苗

（宁波大学 商学院，浙江 宁波 315211）

1 问题提出

在中国，机动车辆保险是财产保险中的一个新兴门类。近几年，随着国内汽车市场的快速增长和车险投保意识的逐步提高，中国机动车辆保险保费收入稳步增长，已逐步成为我国财产保险公司的重要支柱险种。对中国车险市场外部环境的研究表明，车险保费收入增长具有良好的基础。《中华人民共和国2009年国民经济和社会发展统计公报》显示，2009年末，全国民用汽车保有量达到7619万辆（包括三轮汽车和低速货车1331万辆），比上年末增长17.8%，其中民用轿车保有量3136万辆，增长28.6%。与之对应，机动车辆保险保费收入达到6000亿元人民币左右。但同时，中国机动车辆保险市场面临赔付率一直高企且呈上升趋势的困境，导致财产保险公司的赔付压力过大,赢利水平明显下降。全面提升经营机动车辆保险的核心竞争力,始终是我国财产保险公司的重心。如何防范和控制机动车辆保险经营风险，提升盈利能力是目前各财产保险公司的重要任务。而降低赔付率，很重要的一步就是加强承保管理工作，建立和健全核保制度并保证得到有效实施。本文针对这一问题，从实证的角度，对我国机动车辆保险核保系统的构建进行了研究。

2 研究方法介绍

由于Logit模型较为普遍，而且实现它的软件也非常多。Logit模型是利用标准化logistic分配的累积分配函数（简称C.D.F）来转换P的值，使之介于0～1之间。

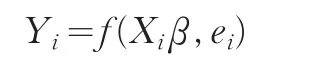
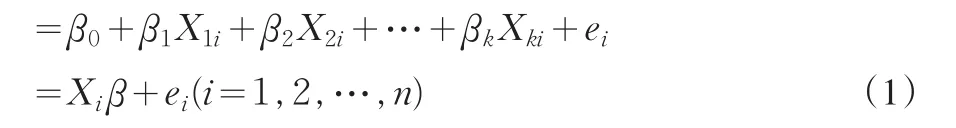
其中：

Yi=1，第i张保单通过核保；

Yi=0，第i张保单未通过核保；

Xki：影响第i张保单是否通过核保的第k个解释变量；

Xi：影响第i张保单是否通过核保的解释向量；

：参数向量；

ei：干扰项，服从二项分布b(0,p(1-p))。

另外，Pi为第i张保单有通过核保倾向的概率，即：

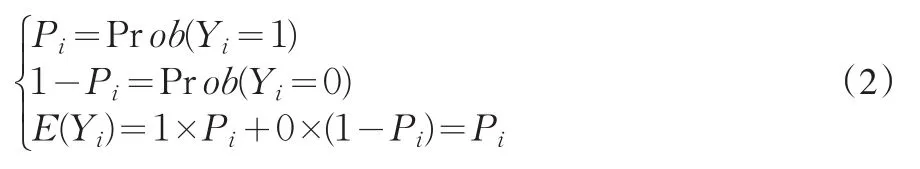
可将Pi写成：

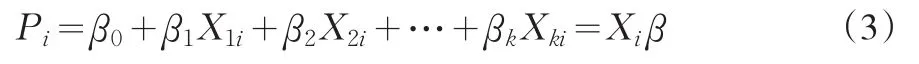
但是式（3）中的Pi值，并不能保证一定落在0～1之间，因此还须经由累积分配函数（C.D.F.）来转换Pi值，才能求出介于0与1之间倾向概率值，故可将上式写成：

将（4）式、（5）式合并，可得：

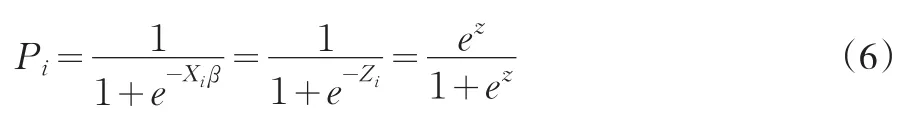
由（6）式转换可得：

对（7）式两边取对数得：

式（8）便是Logit模型。式中的回归系数β并不同于一般的回归系数，它并不能直接反映出解释变量变动一单位使得核保通过的倾向概率变动的单位数，而它表示解释变量的变动对累计logistic分配反函数的影响。

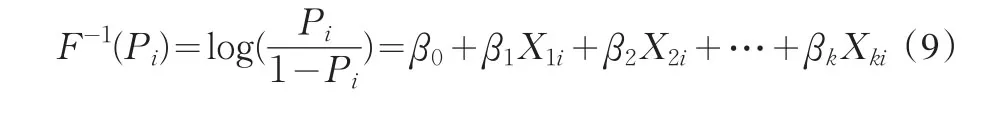
而其概率的变动与解释变量及回归系数的函数息息相关。它可表示为：

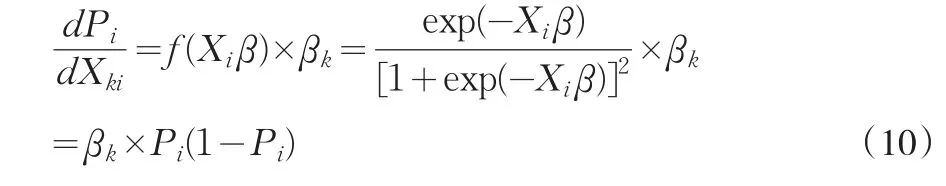
Logit模型就是基于决策者对事件发生概率的二元判断，根据二元Logit建模的要求应设X1,X2,…,Xk是与Y相关的解释变量，假定获取的n组样本数据为(Xi1,Xi2,…,Xik;Yi)，Yi是取值0或1的随机变量。则二元Logit回归的极大似然估计就是要找出因变量与解释变量的相关度，在本研究中，也就是找出“保单i通过核保倾向的强弱Y”与“影响其是否通过核保的因素XK”之间的因果关系。

3 数据来源与相关解释变量

出于数据的局限，我们选取了我国某一家具有代表性的财产险公司2007年以来在核保工作系统中仍有保存的2132条未通过核保的相关记录作为一个子样本，为求实证的精确度与绩效，本实证采取2：1的比率配对，选择资料完整的部分，即未通过核保的共1821笔，通过核保的则随机抽取3642笔；样本内有4048笔，其中未通过核保有1400笔，通过核保的有2648笔；样本外有1415笔，包含通过核保的994笔,未通过核保421笔。本实证使用的变量名称及定义如表1所示。附带说明的是，通过我们向该财产险公司核保岗位的有关人员了解，一般来说，每年车险的核保通过率都很高，但近年来，随着保险公司风险管理意识的逐步加强，该比率已有明显下降，被拒保车辆也逐年增加，同时对于核保岗位人员的考核也越来越严格。

有关变量的解释如下：

（1）核保结果变量（Y）：核保通过：1，核保不通过：0

（2）被保险人性质（X1）：被保险人为法人或组织：1，被保险人为个人：0

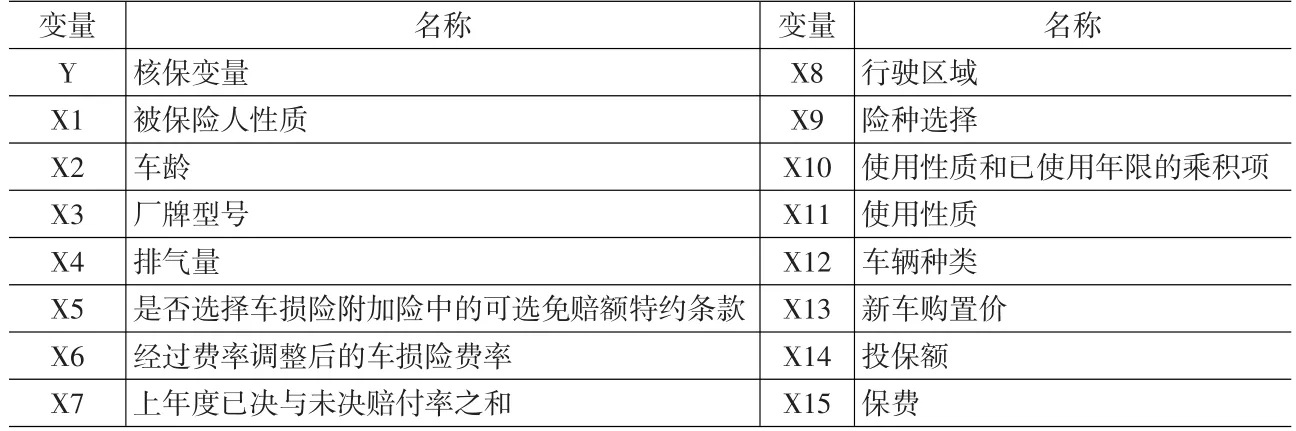
表1 变量名称一览表

（3）车龄（X2）：被保险车辆的已使用年限，车龄越高，核保通过率越低

（4）厂牌型号（X3）：被保险车辆为进口车：1，国产车：0

（5）排气量（X4）：按照实际资料处理

（6）是否选择车损险附加险中的可选免赔额特约条款（X5）：如果选择该条款（说明存在自负额）：1，否则：0

（7）经过费率调整后的车损险费率（X6）：以标准费率为基础经浮动修正后的实际费率为准

（8）上年度已决与未决赔付率之和（X7）：一般来说，该值越高，核保不通过的可能性越大

（9）行驶区域（X8）：省内行驶：1，否则：0

（10）险种选择（X9）：被保险车辆只投保了主险：1，除主险之外还投保了附加险：0

（11）使用性质和已使用年限的乘积项（X10）：对使用性质为USE-1：家庭自用，USE-2：非营业用（不含家庭自用），USE-3：公路客运、旅游客运、公交客运，USE-4：使用性质为出租/租赁，和USE-5：使用性质为营业性客货运分别赋值1，2，3，4，5之后与已机动车辆已使用年限相乘之后的所得值

（12）使用性质（X11）：被保险车辆的使用性质为营业用车：1，否则：0

（13）车辆种类（X12）：被保险车辆为货车：1，否则：0

（14）新车购置价（X13）：新车购置价越高，通过核保的可能性越高

（15）投保额（X14）：一般来说，投保额越高，保险公司可以征收的保费也越高，而保费越高，通过核保的可能性也越大，但是，在我国大多数保险公司，对于那些高风险车辆，通常会限制其最高投保额，各地产险公司也会有自己特别的规定，所以说那些往往投保高额保险的高风险车辆，遭受拒保的可能性也比较大

（16）保费（X15）：保费越高，通过核保的可能性越高。

4 变量检验与实证结果分析

4.1 各变量是否对核保通过的差异性检验

在检验各变量中，是否对核保通过与否存在显著差异，我们通过SPSS10.0列联表分析（CROSSTABS）进行检验，列联表分析主要功能是分析各事务、现象的差异性，与以前分析差异显著性分析方法不同，列联表分析生成二维和多维交叉表。因此，它可以分析一个行变量和一个列变量的差异性。由于Crosstabs过程中的变量是分组变量，若使用连续型变量作列联表，则必须先对变量进行分组，可自己事先按照常理进行分组（本文采用自行分组），也可用Record过程（选择“Transform”→“Record”→“Into same Variable”）对数据重新编码。检验结果如表2所示。由统计结果，我们发现只有变量X3厂牌型号不存在显著差异，其他变量均对核保与否存在显著差异。例如，检验变量X1，即不同性质的被保险人是否对核保通过与否有显著差异，通过交叉分析表，可得出Pearson Chi-square值为7.468，自由度为1，p-value（双尾）为0.011，因此拒绝原假设，这表示不同性质的被保险人对核保与否有显著差异。

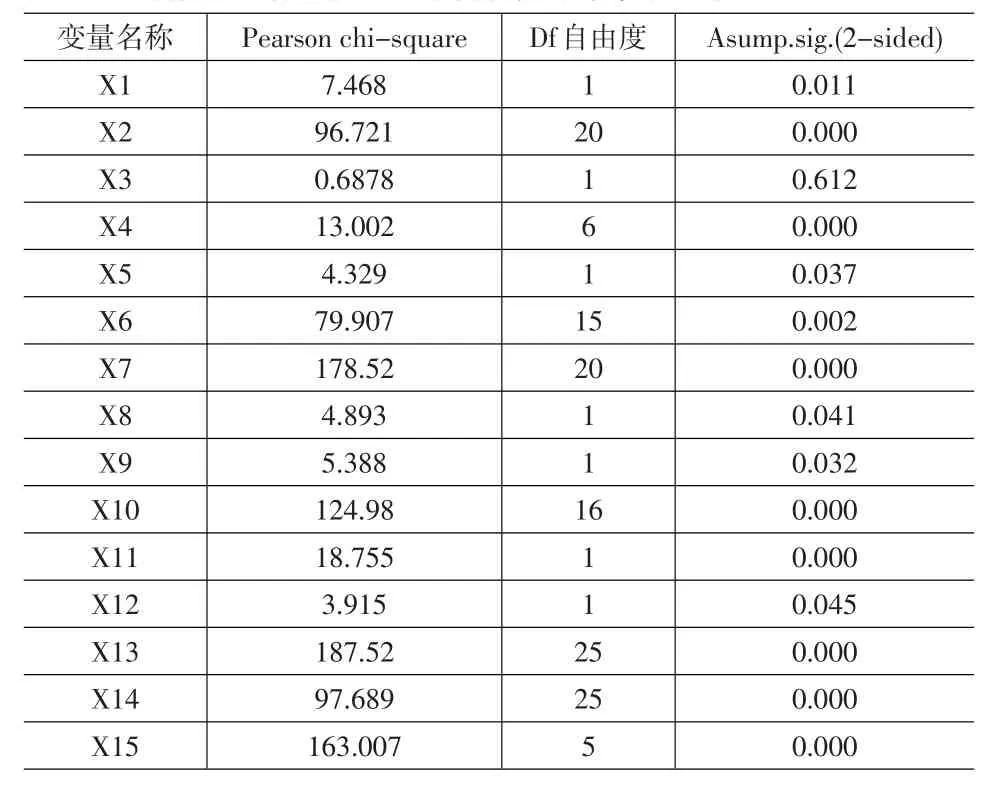
表2 各变量是否对核保通过与否的差异性检验结果

4.2 正态分布检验

利用K-S检验汽车核保变量是否符合正态性，并以α=0.05为显著性水平的标准，分别针对各个变量分别作正态性检验，若各个变量都符合正态性检验，则称此变量符合正态性检验：

H0：汽车核保变量符合正态分布；H1：汽车核保变量不符合正态分布实际检验结果，我们可以看出，全部都拒绝H0，表示所有的汽车核保变量皆不服从正态分布。由于这个结果是显而易见的，所以我们不将统计表列入文中。

4.3 两样本均数比较检验

由于上述变量正态性的检验中，因变量皆呈现不符合正态分布假设的结果，故本研究采用非参数分析中的Mann-Whitney U检验（实际就是大家都熟悉的两样本均数比较的检验）来检验两组变量是否有显著差异，显著性水平的标准为α=0.05。

H0：核保通过的保单与核保未通过的保单各变量的均数分布相同

H1：核保通过的保单与核保未通过的保单的均数分布不相同

实证检验结果表明除了是否选择车损险附加险中的可选免赔额特约条款（X5）、投保额（X14）和行驶区域（X8）呈现出无显著差异外，其余皆拒绝H0，即核保通过与否的变量的平均数有显著性差异。

接着，我们应用因子分析法来进行变量的筛选，其目的是将一组变量精简成几个较少且相互独立的变量来代表原先的资料结构，并通过方差极大旋转法进行正交变换，得到因子负荷量，最后可以选取四个成分内因子负荷量最大的变量，分别为X2、X7、X10、X15、因此，便以上述的四个变量作为四个成分的解释变量。

4.4 Logit模型的实证结果分析

首先应用上述的因子分析法筛选出的变量，再加上X1，X9，X11，X12等虚拟变量，即有X1，X2，X7，X9，X10，X11，X12，X15共8个变量来进行Logit模型分析。利用样本内的资料进行Logit模型的分析，并将结果做为样本外测试用，由于常数项不显著，将其去掉，建立不含常数项的模型。参数估计结果如表3所示，由表3中的估计结果显示出所有变量都基本表现显著。

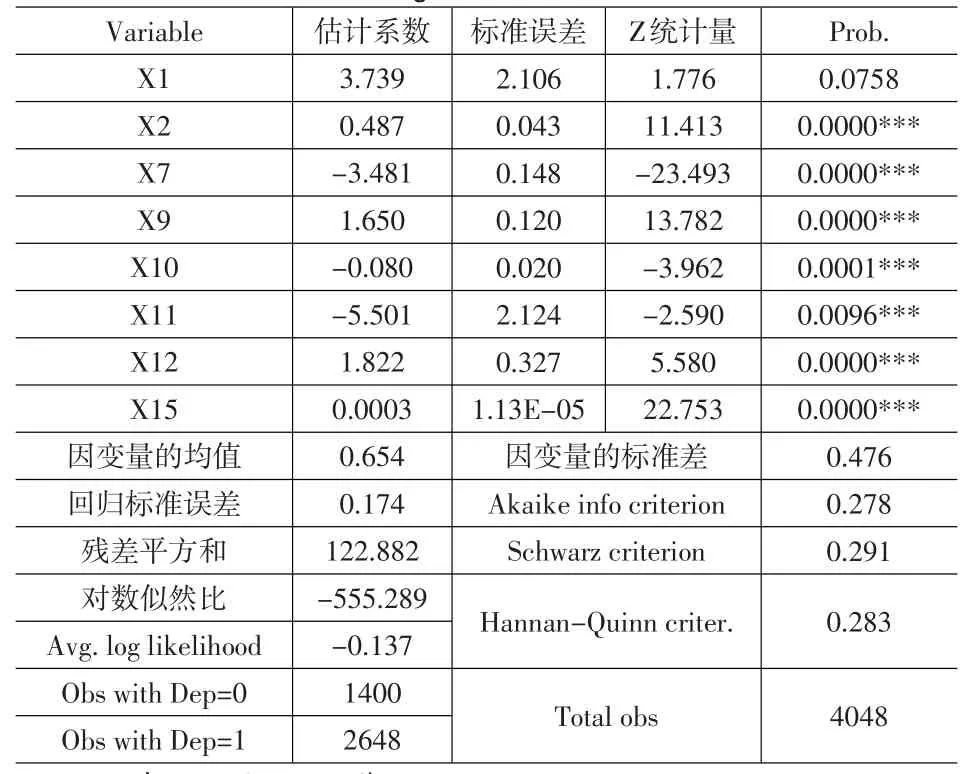
表3 Logit参数估计结果

由Logit模型的参数估计结果，可得出（11）式做为样本外测试。

根据0＜y＜0.5时，判定该保单核保不通过；0.5≤p＜1时，判定该保单核保通过的判定原则,由表6.4的样本内假设判断表可以得知，判断1误差的概率为2.91%，判断2误差的概率为2.79%，总正确率为97.13%，总出错率为2.87%。

而应用（11）式进行样本外预测，由表5的样本外假设判断表可以得知，判断1误差的概率为4.83%，判断2误差的概率为5.23%，而总正确率为95.05%，总出错率为4.95%，总体而言，Logit模型样本内外的判断正确率达到95%以上。

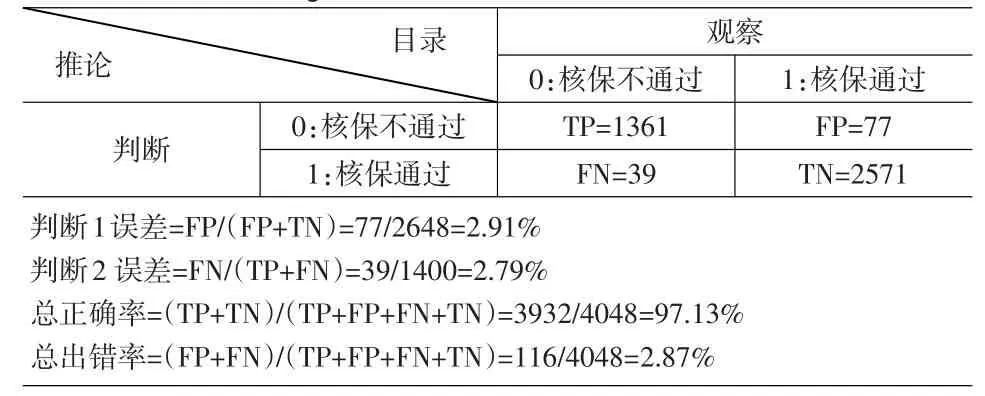
表4 Logit模型——样本内假设判断表

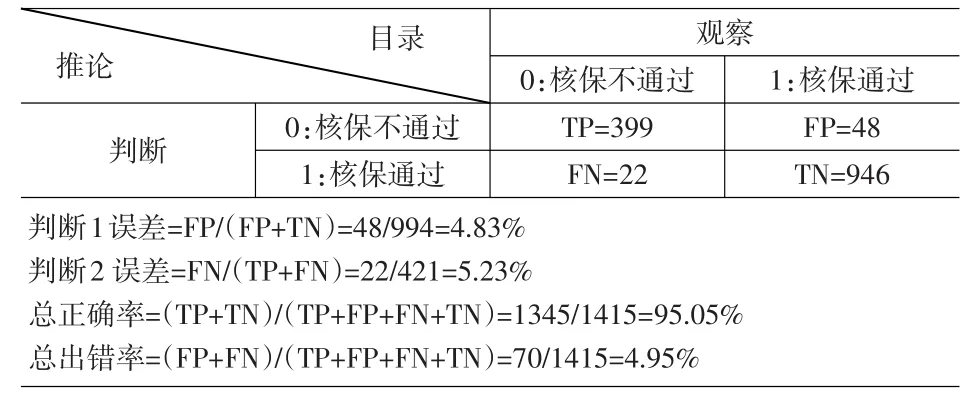
表5 Logit模型—样本外假设判断表

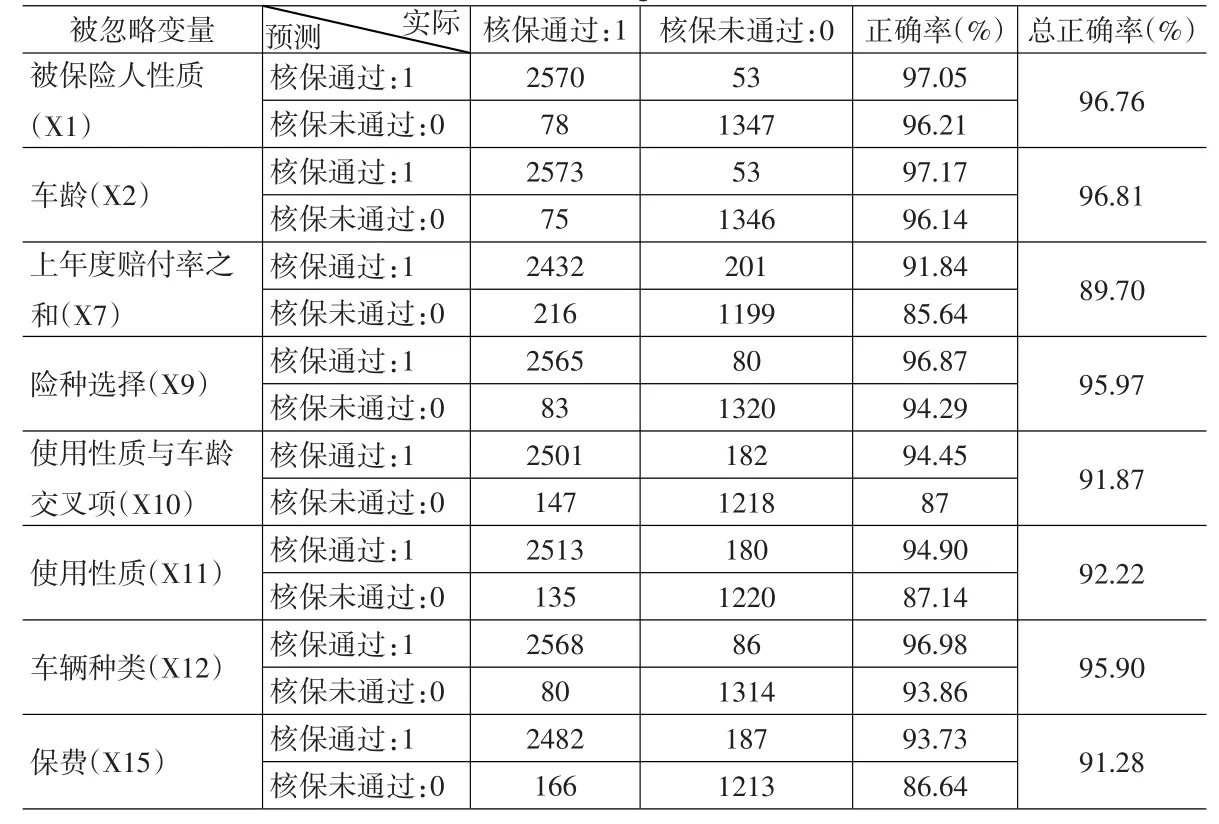
表7 忽略变量后的Logit正确率

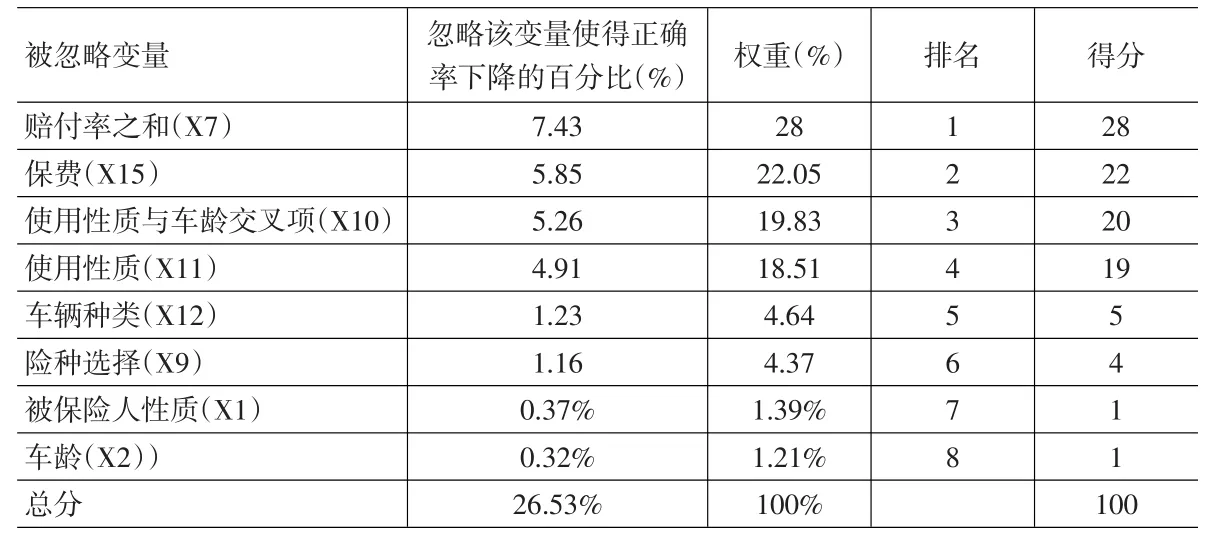
表8 变量重要性排序及得分

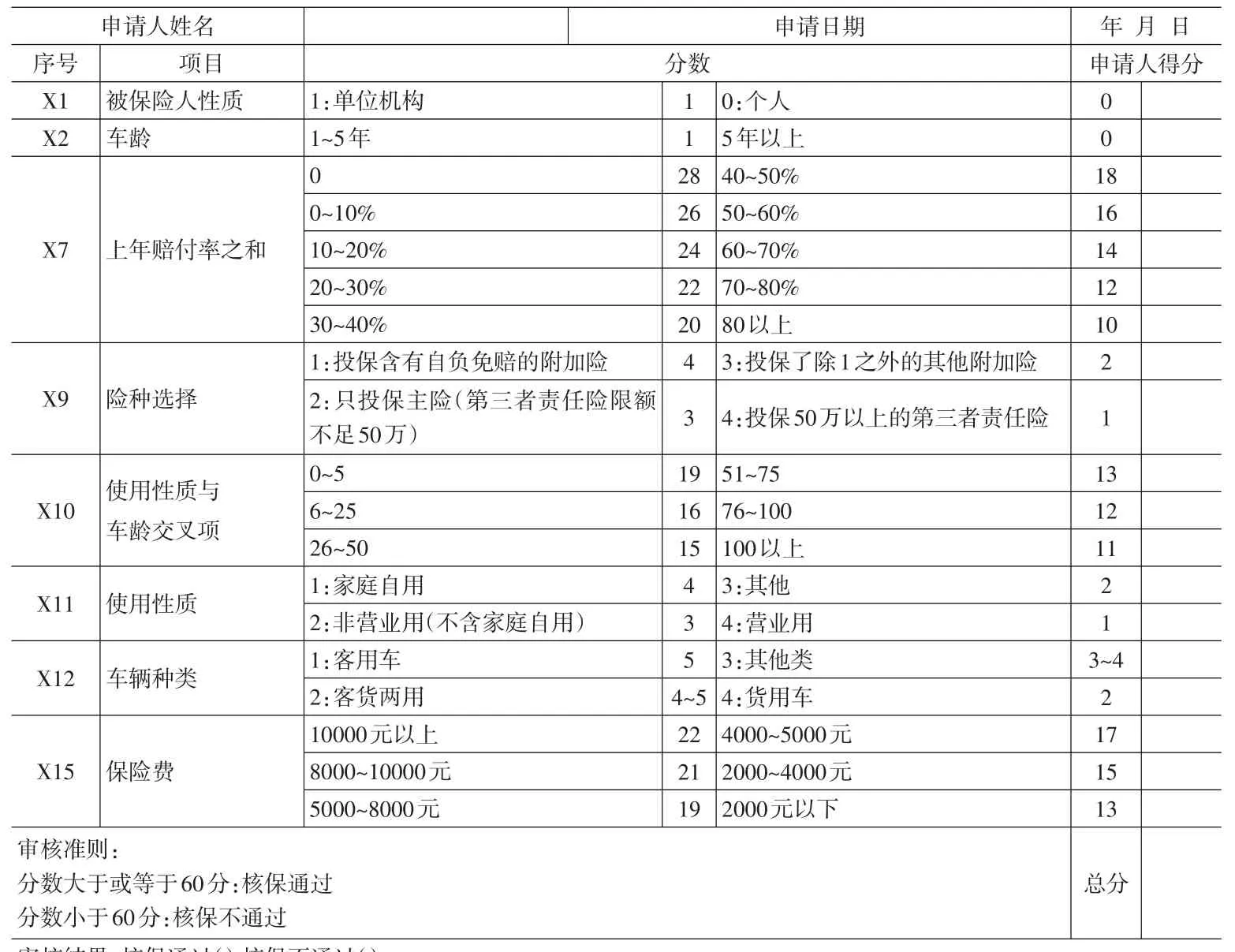
表9 某财产保险公司机动车辆保险核保评分表

5 构建核保评分表

我们接下来要进行的工作就是构建核保评分表。

步骤1：先求出Logit模型剔除相关变量的总正确率，以此确定该变量的重要程度。若剔除变量后，总正确率下降越高，则代表该变量越重要。表7是步骤1的结果，显然，上年度已决与未决赔付率之和（X7）最重要。

步骤2：将Logit模型的总正确率加权平均并排序，总正确率低者，代表该变量越重要，表8为变量重要性排序结果，由表中，我们可以看到重要性依序分别为：

步骤3：根据排名顺序，建构核保评分表。

根据表8的得分表，我们可初步设计出一张核保评分表，如表9所示，表中各项的评分标准目前仍采取主观①目前的评分表仍是初步的构想，分数设定也比较主观且不严谨，有待后续研究。的设定方式，不过它至少可以作为一个评分表初步的构架以供参考。例如，在被保险人性质变量中，被保险人为机构或单位组织，得1分，被保险人为个人，则为0分。对于上一年度已决和未决赔付率一项，我们将评分标准分成10个档次，分别赋值。（当然，如果数据允许的话，我们应根据上三个年度的已决和未决赔付率之和进行评分，这样会更科学和公平。）其他项目依次类推，总分最高为100分，分数达60以上，则通过核保，准予承保②设定60分以上核保通过是根据现有实证资料测试结果设定，仍有待后续更严谨的方法来认定。。

举例而言，表10为某投保人的原始资料透过表6～9的评分表，可求出总分为63分，结果应给予核保通过，予以承保。

步骤4：根据核保评分表，进行测试及修正。

6 结论

由本文以上的讨论及上述的实证结果分析，我们可以获得影响机动车辆核保的最重要因子包括被保险人性质（X1），车龄（X2），上年度已决与未决赔付率之和（X7），险种选择（X9），使用性质与车龄的交叉影响（X10），机动车辆的使用性质（X11），车辆种类（X12）和保险费（X13）。不过由于我们所能获取到的数据的有限性，我们的实证工作不能够做到更细致和更全面的考虑到其他一些也许更为重要的变量（比如说机动车年平均行驶里程数，相关驾驶员及被保险人的个人信息等），这也会引起核保评分结果的偏差。这都有待我们今后的补充研究和发现。

表10 某投保人的核保审核实例

前面已经提过，我国机动车辆保险的赔付率牵动着我国整个财产险损失率的高低，换言之，机动车辆保险的获利与否，关系着整个财产险的经营结果，也同时决定着财产险公司的经营绩效，因此，车辆保险若能建立完善有效的核保系统，非旦可降低其损失率，亦可提升其获利能力。

而本文提出的针对我国机动车辆核保体系提出的可行的计量方法，并据此模型建构一套严谨的核保系统，相信这对理论或实务上均有一定的参考价值，对降低风险必然也有一定的绩效。

[1] 张洪涛，郑功成.保险学[M]北京：中国人民大学出版社，2000.

[2] Chiappori,Pierre-Andre,Bernard Salanie.Empirical Contract Theory:The Case of Insurance Data[J].European Economic Review,1997,（41）.

[3] Crocker,K.J.,A.Snow.The Efficiency Effects of Categorical Discrimination in the Insurance Industry[J].Journal of Political Economy,1986,(94).

[4] Dahlby,Bevan G.Adverse Selection and Statistical Discrimination:An Analysis of Canadian Automobile Insurance[J].Journal of Public Economic,1983,(20).