地价增长率的GM(1,1)预测模型

闫海波，陈敬良

（上海理工大学管理学院，上海200093）

1 地价增长率与GM(1,1)建模

1.1 地价增长率

房价问题是当前理论和现实的热点问题。而地价是房价的核心构成要素。从某种意义上讲，房价问题就是地价问题。房价的增长率几乎是地价增长率的递推与映射。地价增长率对于国家宏观经济政策、企业的战略决策、民众理财方式的选择，都是较重要的数据；特别是近期来，我国经济已呈现较明显的通胀形势下，更受到人们普遍关注。因此，研究地价及其变化规律，具有一定的理论和现实意义。

地价增长率主要反映地价水平的变化程度，使用简单的统计学方法，计算公式为：地价增长率(%)=（当期平均地价－前一期平均地价)÷前一期平均地价×100%。

1.2 GM(1,1)预测模型

GM(1,1)预测模型是以灰色系统理论为基础，通过原始数据的处理和灰色模型的建立,对系统的未来状态作出科学的定量预测的一种方法；目前较为成熟的预测方法已超过200种，各种不同的预测方法有其所适用的特定对象,不存在一种普遍“最好”的预测方法。之所以采用GM(1,1)模型是基于以下二个方面的考量：第一，目前的预测方法多以数理统计为基础，对样本量有较高的要求。市场经济条件下地价增长率只有短短三十年的数据，不满足大样本数理统计的要求。而GM(1.1)模型则对数据要求较低，可以完成小样本条件下的预测，理论上讲，GM(1,1)只要求4个数据便可以完成建模与预测，这是其他统计方法不可比拟的；第二,计算量相对较小,普通电脑即可完成计算；第三，经过检验，地价增长率的预测值与实现情况拟合度较高，方法较为实用。

2 GM(1,1)模型的建模原理

GM(1,1)中的前一个1，实际是n=1，即1阶导数，后一个1是指一个变量。因此用GM(1,1)模型来预测地价增长率，是针对时间序列建模，是一个微分、差分和指数兼容的模型。地价增长率灰色模型GM(1,1)建模条件如下：

(1)地价增长率的原始数列是等时间序列，即Δk=Δkt-Δkt-1=1(为常数，表示时间间隔)

(2)GM(1,1)模型，当k≥4时,具有延展性。

(3)原始数列为非负序列。

首先给定原始数据：x(0)(k),k=1,2,…,n，为每年地价增长率的数据序列，记为：

x(0)=(x(0)(1),x(0)(2),…x(0)(n))，对x(0)做累加生成（I-AGO）：

于是有生成序列：

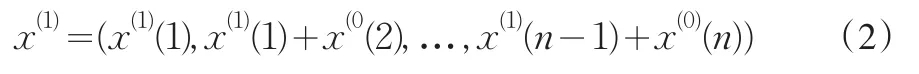
由x(1)建立白化微分方程：

此为GM(1,1)模型的实质。其中，a、b称为发展系数和灰色作用量。设为向量参数，=(a,b)T

可用最小二乘法取得。

其中，B是由1-AGO的紧邻均值生成的矩阵，其结构如下：

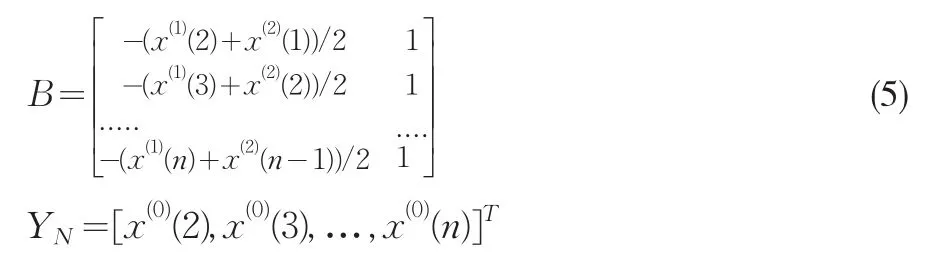
而YN等于原始序列的转秩。

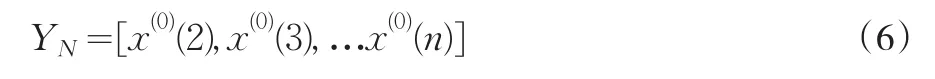
白化形式微分方程的时间响应函数即为预测函数[1]：

x(1)(k+1)=(x(1)(1)-b/u)eak+b/a，其中k=1,2,…,n

灰色模型GM(1,1)的预测结果的精度可用“残差大小检验法”检验。

设x(0)(k)为每年实际的地价增长率，x(1)(k)为根据GM(1,1)模型预测的地价增长率，则E(k)为相对误差。

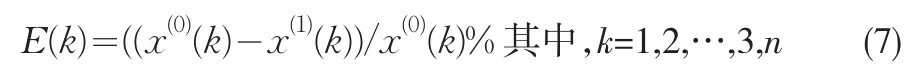
3 地价增长率的GM(1,1)模型的建模过程

经济数据的变化常常具有周期性,因此数据量并非越大越好,根据地价增长率数据的变化特点，采用GM(1,1)残差修正模型进行预测，能够取得较好的预测结果。以2001年为基期，2002年至2008年的全国地价增长率统计如表1所示。x（(0)(k)是原始数据列，x（(1)(k)为累加之后的数据列。

表1 地价增长率数据

由图1可知，地价增值率的原始数列毫无规律，异常离散，而累加之后却呈现出类似S型增长的规律性。也就是说，累加生产使得数据变得有规律，削弱了随机性，从而使得预测变得可能。由公式（5）(6)计算得出：

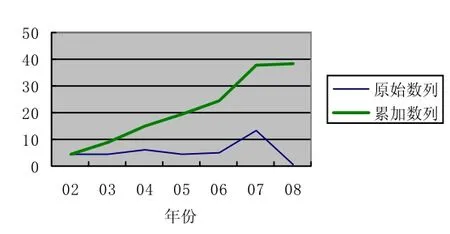
图1 原始数列与累加数列

最终的时间响应函数x(1)(k+1)=(x(0)(1)-b/a)e-ak+b/a=(4.39-5.51/0.04)e-0.01k-5.51/0.01;

根据此函数,预测2002年～2008年土地增长率的预测值和实际值比较结果如表2所示，其中，x1(0)(k)为预测值。

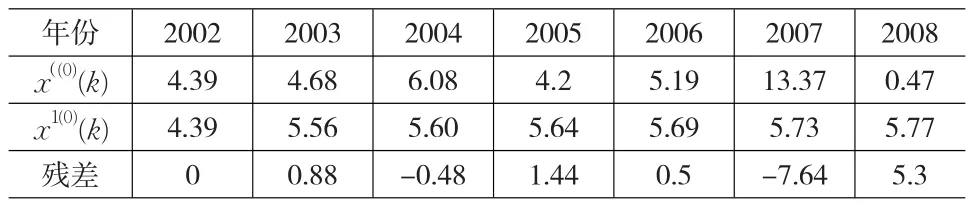
表2 初步预测结果

由表2可知，残差较大，预测精度不尽满意。进而考虑残差的GM(1,1)模型，对原模型进行修正。

所谓残差GM(1,1)模型，就是对残差进行建模，生成时间响应函数，从而形成对原响应函数的修正。残差模型一般只注意修正预测原点附近的数，而不要求修正所有的数。2008年为预测原点，可取2005年～2008年的残差进行二次GM(1,1)建模。

此时，残差GM(1,1)模型中的a=-0.3806,b=1.9835;

时间响应函数为

q1(1)(k+1)=(q(0)(1)-b/a)e-ak+b/a=(1.44+1.9835/0.3806)e0.3806k+1.9835/0.3806

对上式取导数，得q1(0)(k+1)=0.3806*(1.44+1.9835/0.3806)e0.3806k=6.65e0.03806k。

对x(1)(k+1)求导数，得x1(0)(k+1)=-0.01*(4.39-5.51/0.04)e-0.01k=1.336e-0.01k

综合以上两式，得修正之后的模型为:

x(1)(k+1)=1.336e-0.01k-β(k-4)6.65e0.03806k

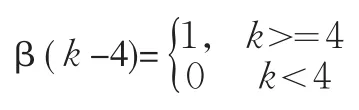
根据此模型，在预测点2008年以后的2年，地价增长率分别为5.87%,7.83%。

实际的地价增长率为5.05%，8.8%（2010年前三个季度）。预测结果可以接受。

4 结论

根据模型的预测结果，全国综合地价增长率将在2012年超过10%，而事实上在2010年第3季度，商业用地地价增长率已经超过了10%。地价不可避免的增长趋势无疑会传导到房价。地价增长率数据是经济系统各部门相互作用的结果，因此数据本身就能够解释自己和经济系统。基于灰色理论的GM(1,1)预测模型预测了地价增长率，与现实拟合度较好。

[1] 邓聚龙.灰色系统基本方法[M].武汉:华中科技大学出版社,1988,(40).

[2] 凌学文,李树刚,任海峰.GM(1,1)模型在市场需求预测中的应用[J].西安科技学院学报,2003,(12).

[3] 郑荣臻.企业商品交易价格指数的GM(1.1)预测模型[J].时代金融,2008,(7).