基于社会零售总额的非正常波动统计数据的季节调整

翁东东

（泉州师范学院，福建 泉州 362000）

0 引言

我国学者对非正常波动统计数据季节调整方法应用的系统研究相对较晚，目前实际操作是采取与上年同期的数据进行比较的方法来反映经济的增长变化，如采用月同比的居民消费价格指数反映价格变动的一般趋势，这种方法可以消除季节性因素的影响，但有它的局限性，即不能及时反映经济变化的转折点，并可能产生错误的结论[1]。研究表明，采用不经过数据季节调整（修匀）的数据与去年同期进行比较所反映的经济周期的转折点往往要平均滞后六个月。直到上世纪90年代，我国统计学理论界和政府统计系统的相关人士才开始接触非正常统计数据季节调整（修匀）模型，但对其研究不够深入。因此，研究由于季节、节假日或其他特殊原因导致的非正常波动统计数据季节调整方法，解决这些统计数据如何剔除非正常因素的问题，是我国迫切需要解决的一个重要课题[2]。这一研究不仅对准确计算相关统计数据有十分重要的理论意义，而且对我们统计实际工作过程中可操作性强的具体处理方法、历史数据的可比性以及探索经济变化的规律都有重要的现实意义。

目前，国内外学者对非正常波动统计数据季节调整的方法大致包括指数平滑法和X-12-ARIMA季节调整方法【3】。国内有些学者运用X-12-ARIMA季节调整方法对消费价格指数等时间序列数据进行数据修匀研究，如张鸣芳等（2004）以上海的月度数据为例，在考虑春节效应的情况下，使用TRAMO/SEATS程序对CPI进行了季节调整，但对调整后的数据没有做进一步的分析【4】。栾惠德（2007）在明确界定CPI的性质及其处理方法的基础上，对我国月度CPI数据进行了季节调整【5】。此外，张鸣芳（2005）也对中国季度GDP的季节调整作出简要的分析，她认为中国GDP有显著的季度间季节性变动特征,但不存在年度间的变动季节性特征，即显现出非常有规律的季度季节性变动【6】。

1 非正常波动统计数据季节调整方法选择与数据检验

本文采用的定量方法包括指数平滑法、单位根检验、协整检验、向量自回归等方法，对数据季节调整方法研究以总量指标和相对指标为例予以研究，其中总量指标数据季节调整可归为单变量时间序列季节调整，相对指标数据季节调整可归为多变量时间序列修匀。本文总量指标以历年我国社会消费品零售总额为例予以例证；相对指标以居民消费价格指数（环比和定基）与工业品出厂价格指数（环比与定基）为例予以实证。在实证中对建立的修匀模型得出的修匀值与实际情况进行比较，同时，在建模前首先对研究对象作单位根检验，随后建立相应的向量自回归（VAR）。

1.1 向量自回归模型

向量自回归(VAR)模型是基于数据的处理多个相关经济指标关系的重要模型之一，并且在一定的条件下，多元MA和ARMA模型也可转化成VAR模型。向量自回归模型通常要求回归中的变量是平稳的，如果变量是非平稳的，则可以考虑利用向量离差修正模型【7】。就本文所研究的CPI和PPI数据而言，符合上述模型的适用条件：（1）研究的CPI和PPI数据都属于宏观经济数据；（2）选取的数据是2005年1月～2010年3月的CPI和PPI环比定基数据，样本容量为63个，达到了应用VAR模型的要求；（3）由单位根检验结果可知环比的居民消费价格指数（CPI）与工业品出厂价格指数（PPI）都为平稳变量。

1.2 数据的平稳性检验分析

用ADF单位根检验方法来分析数据的平稳特征。各数据均为我国的相关经济指标数据，其中定基指数将2004年12月的水平定义为100，包括：社会消费品零售总额、居民消费环比价格指数（以上月价格为100）、居民消费定基价格指数（2004年12月价格为100）、工业品出厂环比价格指数（以上月价格为100）和工业品出厂环比价格指数（2004年12月价格为100），数据均为2005年1月～2010年3月的月度数据。

经典计量回归模型是建立在稳定数据变量基础上的，对非稳定变量使用经典回归模型，可能会出现虚假回归问题。但是，如果变量之间有着长期的稳定关系，即它们之间是协整关系，可以使用经典回归模型方法建立回归模型。为此，本文对有关变量进行了ADF单位根检验和估计模型的协整检验。

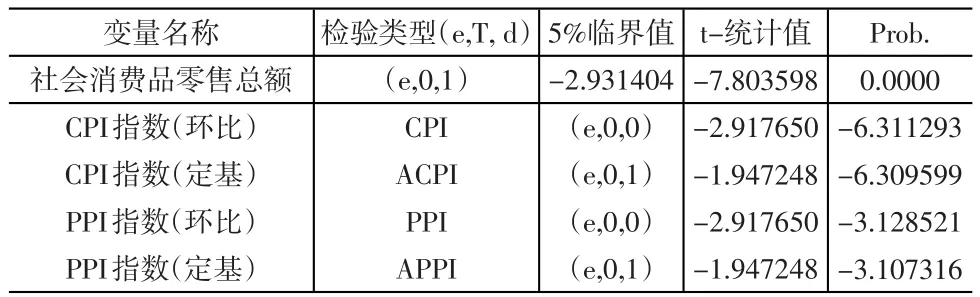
表2 有关变量的Augmented Dickey-Fuller(ADF)单位根检验

由表2的ADF单位根检验结果可知在5%的置信水平条件下，社会消费品零售总额、定期CPI（以2004年12月价格为100）和定期PPI（以2004年12月价格为100）需要差分一次后为平稳变量，因此他们都为I(1)。而环比CPI（以上月价格为100）、环比PPI（以上月价格为100）是平稳的，即I(0)。

2 非正常波动时间序列数据修匀方法实证分析

2.1 总量指标季节调整实证分析

在对上述指标进行平稳性检验后，笔者认为我国社会消费品零售总额具有直线趋势，为一阶单整，故社会消费品零售总额（e,0,1）用一阶差分指数平滑法较为合适。在此基础上，以2005年1月～2010年3月的社会我国消费品零售总额数据为例，具体数据见表3。从表3中的我国社会消费品零售总额数据来看，这一时期的时间序列数据总体趋势明显向上。因此，平滑系数α应当取大小适宜的数值，一般在0.3～0.5之间【8】。

从图1所展现的时间序列变动趋势来看，我国社会消费品零售总额总体呈现直线向上态势。当时间序列的变动具有直线趋势时，用一次指数平滑法会出现滞后偏差，其原因主要是给定的数据不能直接满足一次指数模型的要求。我们可以运用一阶差分先对给定的时间序列数据进行处理，使之能够适合一次指数平滑模型要求，然后再对处理后的结果做返回处理。具体公式如下【9】。

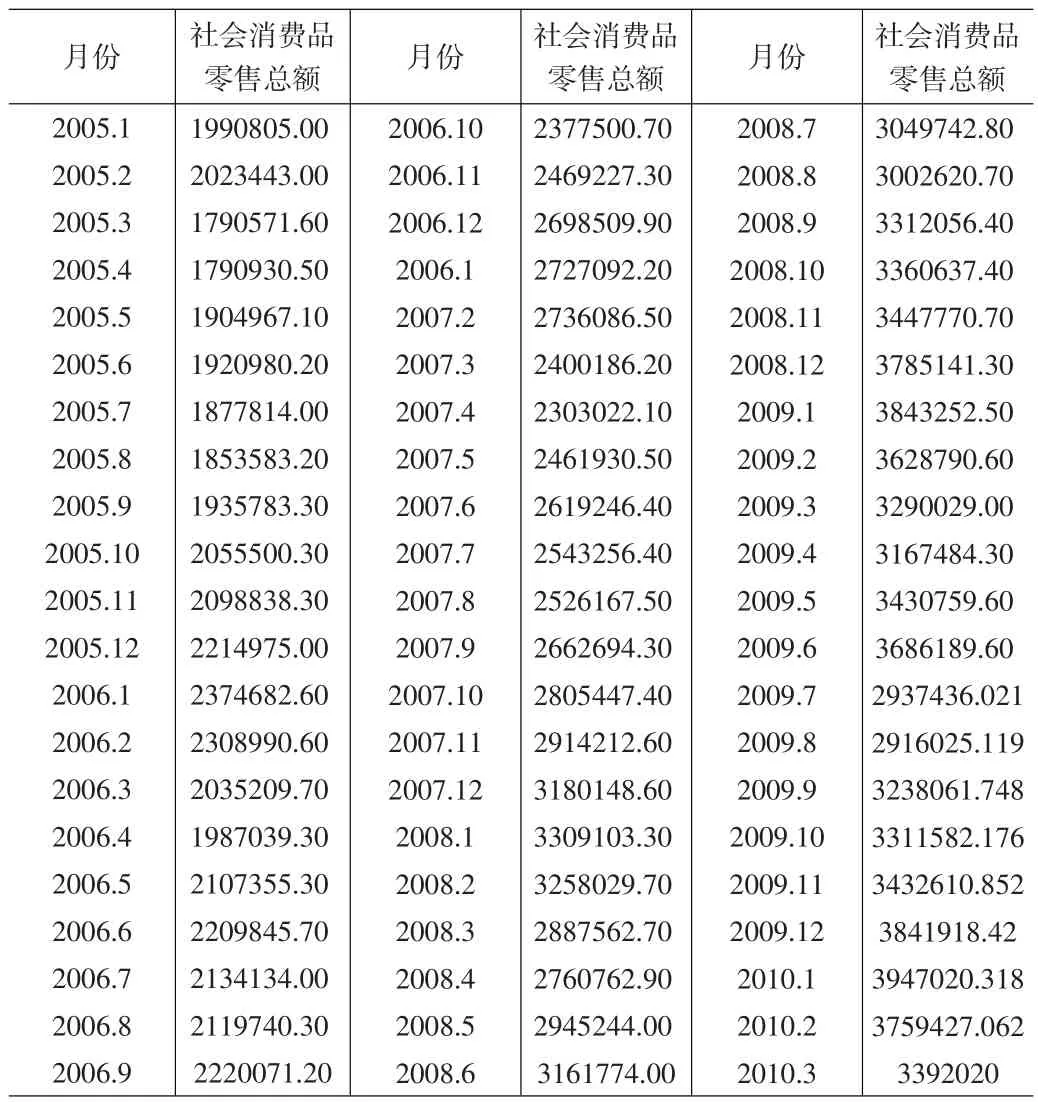
表3 2005年1月～2010年3月我国社会消费品零售总额数据 （单位：万元）

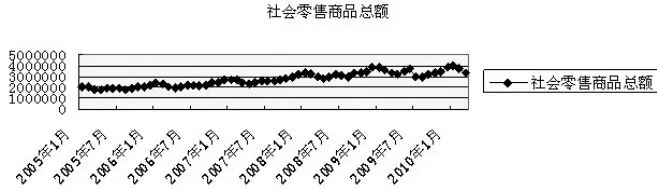
图1 2005年1月～2010年3月我国社会消费品零售总额趋势图

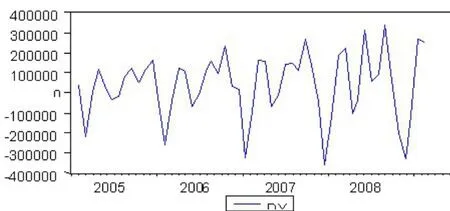
图2 2005年1月～2010年3月我国社会消费品零售总额一阶差分序列图

一阶差分公式：

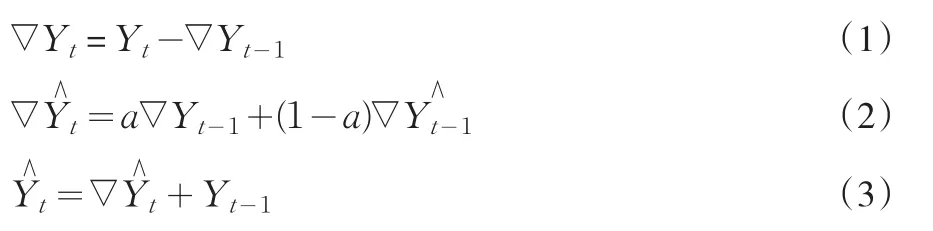
因此，我们首先利用Eviews 5软件对2005年1月～2010年3月我国社会消费品零售总额进行一阶差分处理，结果如图2所示。从图2我们可以看出，处理后的时间序列平稳性较好，基本符合平稳时间序列的要求。然后我们再利用Eviews 5软件对表3中的时间序列数据进行指数平滑处理，输出结果表明：上述时间序列数据模型的平滑系数（即Alpha）为0.4900，残差平方和为30.16720，预测离差的均方根为0.747430，均值为733557.8，趋势项为30.37037。其中，该时间序列模型的平滑系数小于0.5，符合本文前面所提出的指数平滑系数选择标准。那么，我们可以得出我国社会消费品零售总额指标的季节调整模型为：

图3 数据修匀前后的社会消费品零售总额趋势对应图（单位：万元）

2.2 相对指标季节调整实证分析

向量自回归模型通常要求回归中的变量是平稳的，如果变量是非平稳的，则可以考虑利用向量离差调整模型。对于环比价格指数与定基价格指数通常会有不同的平稳特性，为了同时说明不同平稳数据的处理程序，考虑到CPI与PPI都是两个相互关联的重要经济指标。因此，本文分别对环比和定基的CPI指数和PPI指数进行数据处理，并在所得结果基础上给出VAR模型的适用环境的选择建议。

2.2.1 相对平稳波动的数据季节调整方法实证分析

由前面的单位根检验知环比的居民消费价格指数（CPI）与工业品出厂价格指数（PPI）都为平稳变量，因此可以对其直接建立VAR模型，定义各变量在VAR模型中的先后顺序依次为CPI、PPI，则yt=(CPIt，PPIt)T。

VAR模型中一个重要的问题就是滞后阶数的确定。在选择滞后阶数p时，一方面想使滞后阶数足够大，以便能完整反映所构造模型的动态特征。另一方面，滞后阶数越大，需要估计的参数也就越多，模型的自由度就越小。所以通常进行选择时，需要综合考虑，既要有足够数目的滞后项，又要有足够数目的自由度。通过观察该组变量所构成的VAR模型的单位圆图发现，当滞后结束大于等于10时，模型便不具有稳定性，综合考虑极大似然值准则LR，选择滞后阶数为9。通过建立VAR(9)，得到模型结果，从而得知该VAR(9)模型(式（6）)特征多项式的逆根都在单位圆内，因此该VAR(9)模型是稳定的，可以用其做进一步分析。利用所建的VAR（9）模型可运算出初步调整的CPIt、PPIt序列，后文将对这两列做进一步平滑处理。

2.2.2 季节调整的结果

在此，我们对经VAR（9）模型调整过的序列通过双指数平滑法，做进一步调整。根据指数平滑法理论，结合数据趋势特性，取调整后CPItPPIt的平滑系数为0.2，而调整后的ACPIt、APPI取平滑系数为0.4，可得到的平滑序列图如图5～图8所示。图5～图8中的变量名加后缀-0SM的曲线为调整后的曲线，以图5的环比CPI的调整对比图为例，调整前的CPI曲线波动振幅较大；而调整后的曲线图明显平滑许多，且振幅大幅缩小。通过观察其他季节调整后的序列曲线与原始序列曲线的对比图，可见其调整后的曲线较平滑，调整效果比较合理。

以2008年2月为例，该月的环比CPI调整前的数值为102.9，利用所建的VAR（9）模型可运算出初步调整的CPI序列并进行平滑处理后，我们得出季节调整后的相应环比CPI数值为100.2，修匀前后离差为2.7%。这一离差主要是受我国传统消费习惯影响，我国传统节日春节大致在2月前后，在这一阶段内群众消费需求相对增加，导致该月CPI较上月环比大幅度上涨。为了更真实地反映这个月CPI数据的实际变动情况，运用VAR模型对其进行平滑处理，在一定程度上剔除了节假日因素影响，使之更加符合实际情况。

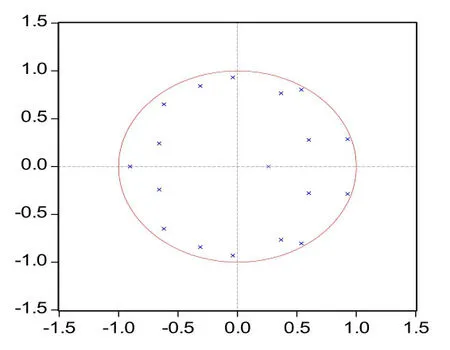
图4 VAR(9)的AR根单位圆图

3 结论与不足之处

根据总量指标的特性，本文采用指数平滑法对非正常波动的福建省社会消费品零售总额数据进行季节调整。其主要结论如下：

(1)季节调整模型

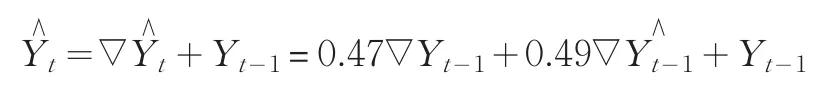
(2)该模型可剔除总量指标（我国社会消费品零售总额数据）非正常波动因素。在实际工作中将相关的时间序列数据代入这一季节调整模型，从而得出相应的时间序列季节调整值，这有助于我们更准确地剔除总量指标（我国社会消费品零售总额数据）非正常波动时间序列数据剔除非正常波动后的实际情况。

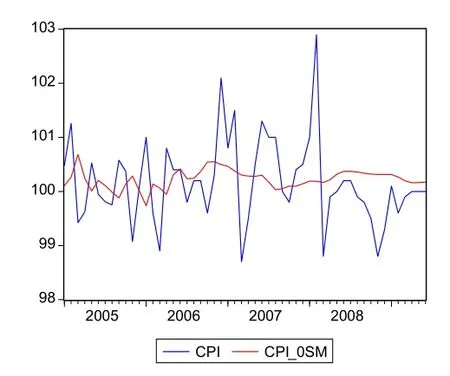
图5 环比CPI数据修匀对比图

图6 环比PPI修匀修匀对比图

图7 定基CPI数据调整对比图

图8 定基PPI数据调整对比图

(3)可直接运用分析软件剔除总量指标非正常波动因素。在目前统计系统常用的软件马克威分析系统或Excel中的均有“指数平滑”分析工具。

（4）可依此办法建立其他总量指标剔除非正常波动因素的模型，也可以直接用建立的模型季节调整非正常波动的总量指标。

根据相对指标的特性，本文采用向量自回归对非正常波动的相对指标（CPI和PPI数据）进行调整。其主要结论如下：

(1)调整模型见公式（4）和（5）。

(2)模型可剔除相对指标（CPI和PPI）的非正常波动因素。在实际工作中将相关的时间序列数据代入这一季节调整模型，从而得出相应的时间序列调整值，这有助于我们更准确地剔除相对指标（CPI和PPI）的非正常波动时间序列数据剔除非正常波动后的实际情况。

(3)可直接运用Eviews、SAS、SPSS等计量分析分析软件剔除相对指标的非正常波动因素。通过上述指标时间序列图季节调整前后的对比分析，调整后的曲线较平滑，可见其季节调整效果比较好，达到了预期的效果。

本文对非正常波动统计数据修匀方法进行的研究，还存在有待完善之处，主要有以下方面：

（1）现有计量分析软件的不完全适合性。目前通用的经济计量软件多数是国外引进的，对季节和移动假日等因素调整时是针对西方的传统因素（如复活节，圣诞节等）进行的，与我国的国情有所不同，比如我国的消费价格指数主要受到的春节、“五一”、“国庆”等假日的影响在模型中就无法剔除。因此，使用一般的计量分析软件直接进行调整时，所得的结果往往不能令人完全满意。

（2）模型的调整值与实际数据有所偏差。对指数平滑法来说，模型最终得出的季节调整预测值的大小跟平滑系数的大小密切相关，而平滑系数的大小与给定的时间序列数据波动程度及其上升或下降的趋势有关。本文主要是利用Eviews计量分析软件对时间序列数据进行平滑处理，数据的波动程度和升降趋势都会对计算得出的平滑系数有影响。因此，个别时间点的数据异常数值可能会导致部分月份的季节调整值与实际数据有所偏差。

[1] Pagan,A.R.Three Econometric Methodologies:An update in L.T.Oxley,C.J.Roberts,D.A.R.George and S.T.Sayer(eds.)Surveys in Econometrics[M].Massa Chusetts:Basil Blackwell,2001.

[2] Markku,L.,H.LüTkepohl.Identifying Monetary Policy Shocks Via Changes in Volatility[J].Journal of Money,Credit and Banking,2008,40(6).

[3] 中国人民银行调查统计司.时间序列X-12-ARIMA季节调整——原理与方法[M].北京：中国金融出版社，2006.

[4] 张鸣芳，项燕霞，齐东军.居民消费价格指数季节调整实证研究[J].财政研究，2003，

[5] 栾惠德.季节调整中的春节模型[J].经济学季刊，2007，6（2）.

[6] 张鸣芳.中国季度GDP季节调整分析[J].财经研究，2005，（7）.

[7] 高铁梅.计量经济分析方法与建模[M].北京：清华大学出版社，2009.

[8] 王长江.指数平滑法中平滑系数的选择研究[J].中北大学学报（自然科学版），2006,(6).

[9] Lütkepohl,H.New Introduction to Multiple Time Series[J].Berlin:Springer Verlag,2005.