基于层次结构模型的小样本组合预测建模

谢 力,魏汝祥,1b，尹相平，訾书宇

（1.海军工程大学 a.装备经济管理系；b.理学院，武汉430033；2.海军装备部 装备招标中心，北京 100071）

0 引言

在预测的实际工作中，有时会碰到一些样本小、波动大的情况，如果直接对其进行预测，往往容易出现拟合效果好而预测效果差的情况。1969年，Bates和Granger[1]提出的组合预测方法，将各种单个预测看作代表不同的信息片段，通过信息的集成分散单个预测特有的不确定性和减少总体不确定性，从而提高预测的精度。目前，关于组合预测的研究主要集中于对同一组数据采用不同预测方法得到的预测结果进行组合，或者对不同来源的性质相异的数据分别建模得到的预测结果进行组合。在这两种研究中，一般认为因为后者利用的信息有本质上的差异，故其组合的效果更佳[2-4]。而要得到多种不同来源、可直接为预测所用的信息往往代价很大或者根本不可行。而实际上，待预测变量的时间序列以及其层次结构的各时间序列往往容易得到。Armstrong[5]、Phelps[6]等人研究发现，分解可以将看起来很难的信号变得简单化。Zellner等人[7]关于GDP增长率以及Marcellino等人[8]对几种欧洲宏观经济变量的预测结果也显示，分解能改进预测的性能。García[9]、Karsten[10]等人分别在交通事故率和欧洲宏观经济变量预测的研究中，都发现使用不同层次信息建模能显著改善预测的效果。George[11]、Mauro[12]等人也对分层组合预测进行了一定的研究。这些研究尽管都涉及到了层次结构的组合预测，但仅局限于对预测变量下层结构分解和综合的研究，事实上，变量的整个层次结构都携带了关于变量的有关信息，应该综合考虑。层次结构模型中的上层结构从更加综合的角度也携带了变量的大量相关信息，且变量本身时间序列所具有的特征也不能忽视。因此，本文主要尝试根据层次结构模型的各种时间序列分别进行预测，从不同层次结构的角度对某一变量进行预测，将不同层次的预测结果与变量本身时间序列预测结果进行组合，以充分利用各相关时间序列所包含的信息，提高小样本预测的稳定性，降低预测风险。

1 层次结构模型

任何系统都是层次分明、有序的结构系统，通过层次结构的构建可以解释其有序结构的内在规律。层次结构模型往往可以把一个复杂的问题通过分解或综合成若干个简单的问题，通过解决一个个简单问题，达到解决复杂问题的目的。其中层次分析法实际上就是主观判断分解的一个非常成功案例。

变量的层次结构实质上是包含了分解和综合两个方面。在时间序列的预测过程中，一个看起来没有什么规律的复杂时间序列，通过层次结构的分解后（下层结构），各成分的时间序列可能规律就比较明显了，成分序列的细节也就会显现出来；同样，通过层次结构中的综合（上层结构）后，也有可能使整体规律更加清晰。层次结构组合预测，先根据主观判断对预测对象构建层次结构，然后对层次结构中的各相关对象分别进行预测，根据将来的相关信息对预测结果进行叠加综合或分解，最后，将通过变量不同层次结构以及相应预测结果与变量原始数据获得的预测结果进行组合，得到最终预测结果。

2 小样本层次结构组合预测建模

组合预测最根本的思想就是充分的利用可获得的信息，提高预测的稳定性，降低预测的风险。在预测的实际工作中，尽管要得到多种不同来源、可直接为预测所用的信息往往代价很大或者根本不可行，但预测变量的时间序列以及其层次结构的各时间序列往往容易得到，我们可以充分利用其层次结构各序列的信息来进行组合预测（见图1）。

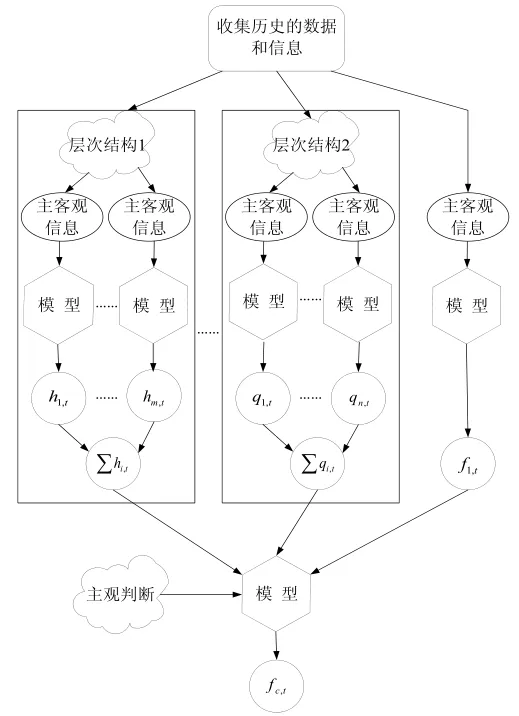
2.1 层次结构构建

在小样本层次结构预测的研究中，由于过高层次的样本往往规律比较复杂，难以准确把握；而过低层次的数据样本往往受噪声的影响会较大，预测的误差也会增大。因此，为了从层次结构中获得有用的信息，降低噪声对过低层次样本的影响和更高层次综合样本信息损失的风险，通常仅考虑待预测变量的邻近层次预测的结果，即向下一层结构和向上一层结构（图2）。

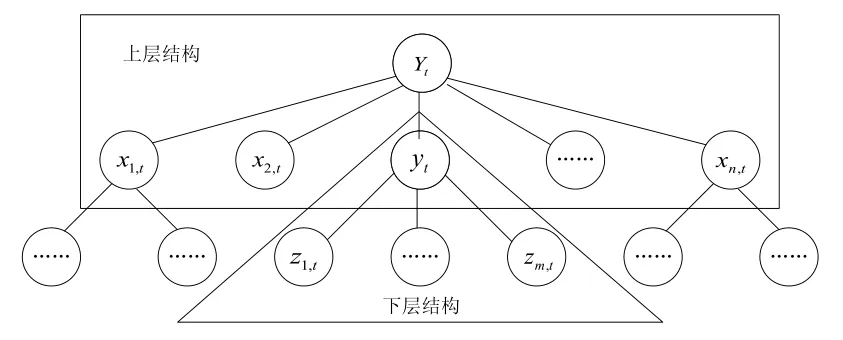
图2 层次结构模型

2.2 上层结构建模

在层次结构模型的上层结构中，设t时刻待预测变量的值为yt，上层综合变量为Yt，构成Yt的其他n个子项分别为xi,t，i=1,…,n。则有

根据上层结构的各子项相关信息（可以是主观判断和各项费用相应的影响因素，也可以是时间序列等），分别构建如下预测模型：

那么，上层结构中，待预测变量yt的预测模型可以表示为

2.3 下层结构建模

在层次结构模型的下层结构中，待预测变量yt可分解为m个子项，分别为zj,t，j=1,…,m。则有

根据下层结构各子项相关信息，分别构建如下预测模型：

那么，向下分解的装备维修费的预测模型可以表示为

2.4 组合预测建模

设t时刻待预测样本数据为yt，通过p种不同方式得到上层结构预测分别为，k=1,…,p；通过q种不同方式得到下层结构的预测值分别为，l=p+1,…,p+q；不分解直接进行预测得到待预测变量的预测值为则yt的组合预测可以表示为

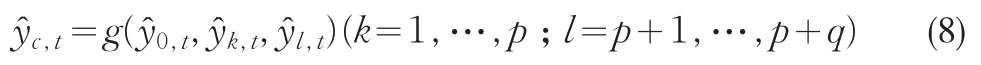
常用的组合预测模型有等权组合、最优方差组合和基于回归的组合等线性组合模型[2-4]，此外，神经网络、模糊系统、遗传规划、自组织算法和神经-模糊系统等非线性组合预测模型也得到了飞速的发展[14]。

3 应用实例

本部分以美国CVN68航母基地级维修费进行预测为例，来验证本文提出方法的有效性。

3.1 层次结构构建

为了简化计算，这里仅选择一种向下分解和一种向上分解方式。根据文献[15]，美国航母维修费主要包括中继级维修费用和基地级维修费用等两部分。基地级修理又可以分为计划修理费用、非计划修理费用和舰队现代化费用。因此，基地级维修费向下可以分解为计划修理费用、非计划修理费用和舰队现代化费用；在其向上分解结构中，CVN68的年度维修费由基地级维修费和中继级维修费构成，各相应的数据见表1。这里我们主要考虑短期预测的情况，选取1978～1994年数据进行建模，并用1995年的数据来测试方法的有效性。

3.2 层次结构预测建模

在García等人[10]的研究中，发现通过分解模型，采用简单方法与更加复杂的方法表现一样好，为了简化计算，所有的预测使用Holt的指数平滑法，运用Eviews 6.0计算。

表1 CVN68年度维修费数据 （98财年，百万美元）

3.2.1 上层结构建模

从表1中的数据可以看出，中继级维修费用远小于基地级维修费用，相差近100倍，故在向上分解结构中，CVN68年度维修费数据规律主要表现为基地级维修费，分解建模意义不大，故该实例中，我们不对向上分解进行建模。

3.2.2 向下分解建模

(1)计划修理费用

根据计划修理的特征，我们认为计划修理一般具有一定的周期，尽管我们不知道美国航母计划修理的确切周期，但从表1中的数据，可以看出其周期应该在7左右，故在采用Holt的指数平滑法建模预测时，选择其季节性周期为7，Holt-Winters-Additive模型。

(2)非计划修理费用

非计划修理费用一般没有明显的季节性，故选择Holt-Winters-No seasonal模型。

(3)舰队现代化费用

根据舰队现代化费用特征，从表1中的数据，可以看出其周期应该在4左右，故在采用Holt的指数平滑法建模预测时，选择其季节性周期为4，Holt-Winters-Additive模型。

(4)主观判断分解预测的综合

根据（5）式，对计划修理费用、非计划修理费用、舰队现代化费用预测结果进行综合。

3.2.3 基地级维修费直接建模

由于基地级维修费分解子项的周期性差异较大，所以基地级维修费时间序列没有明显的周期，选择Holt-Winters-No seasonal模型。

3.3 组合预测

由于等权组合预测计算简单，且在大量组合预测的实证研究中表现出一定的优势[6-7]，这里我们也选择等权组合预测模型对分解预测和直接预测的结果进行组合。组合预测与各单项预测以及原值的比较如图3。

1995年各方法预测值如表2。

表2 1995年预测结果比较

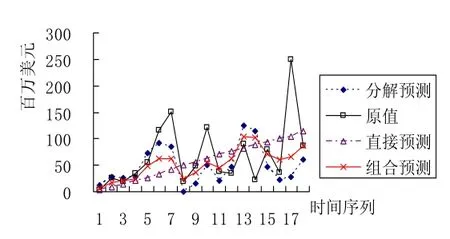
图3 各种预测方法预测效果比较

从表2中可以看出，对于1步向前外推预测，直接预测和分解预测效果相当，且都不太好，而它们的组合预测效果明显得到改进。

4 结束语

（1）本文的建模过程适用于不确定性大、样本小且波动大，相关层次结构信息易获取的预测问题；

（2）基于层次结构模型的组合预测，在整个建模的过程中，能充分利用各层次序列的信息，进而提高小样本预测模型的稳定性，降低预测风险；

（3）在各层次结构序列的特征不太明显，且不能够反映出相应综合性项目所不具有的特征情况下，采用层次结构预测与直接预测差异将不大，层次结构预测失去相应的价值。

（4）本文建模中采用的是加法形式的分解与综合，尽管Collopy等人[16]指出分解成分的乘法综合可能带来爆炸性的误差，具有很大风险，但在特点的背景下，也可以尝试采用乘法形式的分解与综合来进行研究。

[1] Bates J M,Granger C W J.Combination of Forecasts[J].Operations Research Quarterly,1969,20(4).

[2] Armstrong J S.Combining Forecasts:The End of the Beginning or the Beginning of the Eend[J].International Journal of Forecasting,1989,(5).

[3] Graham E,Clive W J G,Allan T.Handbook of Economic Forecasting(Volume I)[M].Netherlands:Amsterdam:Elsevier,2006.

[4] 汪同三,张涛.组合预测——理论、方法及应用[M].北京社会科学文献出版社,2008.

[5] WANG Tong-san,Zhang Tao.Forecast Combination:Theory,Method and Application[C].Social Sciences Academic Press,2008.

[6] Armstrong J S,Denniston W B,Gordon M M.The Use of the Decomposition Principle in Making Judgements[J].Organisational Behaviour and Human Performance,1975,(14).

[7] Phelps R H,Shanteau J.Livestock Judges:How Much Information can an Expert Use?[J].Organisational Behaviour and Human Performance,1978,(21).

[8] Zellner A,Tobias J.A Note on Aggregation,Disaggregation and Forecasting Performance[J].Journal of Forecasting,2000,(19).

[9] Marcellino M,Stock J,Watson M.Macroeconomic Forecasting in the Euro Area:Country Specific Versus Area-wide Information[J].European Economic Review,2003,(47).

[10] Poncela P,Garcia-Ferrer A.The Effects of Disaggregation on Nonstationary I(1)time Series[R].Universidad Autónoma de Madrid,DAEII,Mimeo,2005.

[11] García-Ferrer A,de Juan A,Poncela P.Forecasting Traffic Accidents Using Disaggregated Data[J].International Journal of Forecasting,2006,(22).

[12] Karsten R.Macroeconomic Forecasting in the EMU Does Disaggregate Modeling Improve Forecast Accuracy?[J].Journal of Policy Modeling,2008,(30).

[13] George A,Roman A A,Rob J H.Hierarchical Forecasts for Australian Domestic Tourism[J].International Journal of Forecasting,2009,(25).

[14] Mauro C,Carmine P.A Hierarchical Procedure for the Combination of Forecasts[J].International Journal of Forecasting,2010,26(4).

[15] Christiane L,Bogdan G.Review of Nature-inspired Forecast Combination Techniques[R].United Kingdom:Bournemouth University,2008.

[16] Birkler J,Michael M,John S,et al.The U.S.Aircraft Carrier Industrial Base:Force Structure,Cost,Schedule,and Technology Issues for CVN77[R]. Santa Monica, Calif: RAND Corporation,MR-948-NAVY/OSD,1998.

[17] Collopy F,Armstrong J S.Decomposition by Causal Forces:Using Domain Knowledge to Forecast Highway Deaths[C].Working Paper,1993.