求解VRP的变种群规模混合自适应遗传算法

罗晓明

（华东交通大学 经济管理学院，南昌 330013）

0 引言

车辆路径问题(VRP)是物流系统优化领域一个著名的优化问题。一般意义上的VRP指带有容量约束的车辆路径问题(CVRP)：服务于一个中心出发点的最小费用(如距离、时间等)路径，每个顾客只能被服务一次；而且一辆车服务的顾客数不能超出它的装载能力。其包含两个著名的组合优化问题，即装箱问题(BPP)和旅行商问题(TSP)。VRP至Dautzig和Ramser于1959年首次提出以来，由于其极强的实践背景，引起众多学者的广泛关注[1]。按求解该问题的方法角度来分，大致可分为如下几类研究：精确算法、启发式算法、智能优化算法和计算机仿真等。精确算法是指可求出最优解的算法，包括动态规划法、分枝定界法及切平面法等，但精确算法的计算量随问题规模的增大而呈指数增长，因此只适用于小规模问题[2]。启发式算法一般基于算法设计者经验构造，用来求解相应问题的满意解，启发式算法的优点是能快速地得到满意解，因此常用于NP难题的求解中。传统启发式算法主要有节约算法、最邻近算法、两阶段法及其相互结合而成的混合算法等。众多VRP求解的研究中，遗传算法由于其适用范围广、鲁棒性强、隐含并行性等优良特性而受到学者们的广泛关注。本文拟设计出一种求解VRP的变种群规模的混合自适应遗传算法，一方面，引入可变的种群规模函数控制种群规模的变化；另一方面，提出一种改进的自适应遗传算法，算法中的自适应交叉概率和变异概率考虑了每代个体中不同适应度对算法的作用，这两个参数随算法的进化而自动调整。同时，为弥补遗传算法局部搜索能力差的不足，本文还将C-W节约启发式算法与变种群规模的自适应算法相结合，构造出一种新的混合算法，以解决物流配送的车辆路径问题。

1 VRP问题及其数学模型

VRP问题可描述如下：以容量为Wk的k辆车从一个中心仓库{0}将物品运到n个需求点，每个需求点的物品需求量为gi，i=1,2,…,n；设cij为从节点i到j的距离，与货物重量无关；要求车辆以总运输距离最小为目标来完成运输任务，则其数学模型为

其中：

满足的约束条件如下：

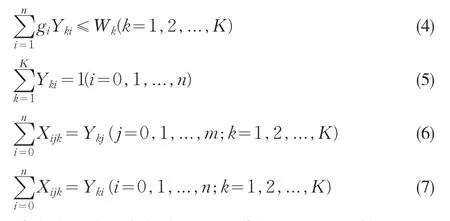
其中式(4)表示每辆车运送的货物量不超出其载重量；式(5)表示每个需求点必须有且只需一辆车送货；式(6)表示若客户点j由车辆k送货，则车辆k必从某点i到达点j；式(7)表示若客户点i由车辆k送货，则车辆k送完该点的货后必达到另一个点j。

2 混合遗传算法的设计

遗传算法的一般步骤为：首先是针对要解决的问题设计染色体编码方案；然后根据编码方案生成初始群体，并在一定的条件下(比如在规定的进化代数之内)进行遗传操作[11]。其中，遗传算子主要包括选择、交叉、及变异三种，选择算子的作用是根据个体的适应度选择种群中的优良个体进入下一代种群；交叉算子在遗传算法中起关键作用，是产生新个体的主要方法；变异运算是产生新个体的辅助方法，它决定了遗传算法的局部搜索能力，同时保持种群的多样性。由于遗传算法局部搜索能力较弱，本文在遗传算法中融入C-W节约启发式算法以改善其局部搜索能力，算法步骤如下。

第一步，编码及产生初始群体。

运用遗传算法求解VRP问题首先要解决的是编码问题。一个解的编码称为一个染色体，组成编码的元素称为基因。本文采用自然数编码方式，设计染色体为V={vi}(i=1,2,…,n)，其中vi表示染色体中的基因，对应于第i个客户号。假设问题中所需车辆数为k，则问题解可表示为k条对应配送子路线，每条子路线由若干需求点所形成的一个排列表示，且每个需求点只能出现在其中的一条子路径中。

按照上述编码规则，染色体的形成包括两个阶段，第一阶段为需求点序列的形成；第二阶段为将该序列可行化，即在满足车辆容量约束的前提下划分子路径[4]。根据文献[4]，首先将随机产生需求点的排列形成集合S，S中元素的个数按初始种群规模确定。然后，对于集合S中的任一元素s，按照车辆的容量及s中的各需求点的商品需求量，将s划分成若干个子序列(即子路径，子路径数不超过k)，这些子路径可构成为问题的一个可行解的染色体个体。例如对一个具有5辆车(每辆车的容量均为W)、10个需求点(商品需求量分别为gi,i=1,2,…,10)的 VRP 问题，假定s为{2,4,6,1,10,9,8,5,3,7}，若g2+g4+g6≤W且g2+g4+g6+g1＞W，则按照上述方法产生的个体的第一个子路径为{2,4,6}，同样按照该方法产生的子路径为{1,10}、{9,8}、{5,3,7}，因此最终产生的一个染色体个体为{2,4,6}，{1,10}，{9,8}，{5,3,7}。在接下来的遗传操作后，均按上述第二阶段的可行化方案进行可行化操作。

第二步，计算适应度函数。

适应度函数的定义一般根据求解问题的目标函数而定，当适应度函数确定后，自然选择规律是按照适应度的大小决定的概率分布来确定哪些染色体适应生存，哪些被淘汰。生存下来的染色体通过遗传操作而产生新的种群。对种群中每一个染色体，首先进行可行化操作得到对应的可行解，然后根据式(1)求得相应的目标函数值Zh，结合已有相关文献及多次试验结果，确定其适应度函数为fh=1/Zh，fh越大则表示Zh性能越好，对应的解越接近最优解。

第三步，确定种群规模。

众多学者对于种群规模的确定进行了研究，如Goldberg[13,14]对最优种群规模进行了理论的分析，Arabas等[15]讨论了变种群规模遗传算法。变种群规模遗传算法中，种群规模由如下公式确定：

其中，popsize(t)代表第t代种群的规模；auxpopsize(t)=ρ×popsize(t)，ρ为繁殖率，一般取ρ为0.4；D(t)代表每代中死亡个体的个数。下面说明D(t)的确定方法。

引入D(t)的目的是为了控制子种群的快速增长，为确定D(t)，必须对个体设置两个相关的参数：一个是个体的年龄age(i)，另一个是个体的寿命lifetime(i)。个体每存活一代则年龄age(i)加1，其存活的代数不能超其寿命值lifetime(i)，寿命值lifetime(i)与个体的适应度有关，高适应度的个体寿命较长，低适应度的个体寿命则较短，个体的寿命值一旦确定则不再改变。当个体的满足时age(i)＞lifetime(i)，个体死亡，由此来确定D(t)的取值。其中，寿命值lifetime(i)的确定比较关键，必须使适应度较好的个体具有较长的寿命，从而限制适应度低于平均水平的个体的发展，因此可定义如下。

若fitness(i)≤averagefitness：

否则：

公式中minLT和maxLT是允许的最小和最大的寿命，按照arabas等[15]的建议，本文取 minLT=1，maxLT=7；minfitness和maxfitness是当前群体最小和最大的适应度，averagefitness代表当前群体的平均适应度。

第四步，遗传操作。

(1)选择

本文采用轮盘选择及精英保留的选择策略。将每代种群中的染色体按适应度fh排序，适应度值最大的染色体直接进入下一代，下一代种群中剩下的染色体用轮盘选择法生成。这样可保证最优个体可以生存到下一代，既给了适应度较大的个体较大的机会进入下一代，又避免了个体间因适应度值不同而被选入下一代的机会悬殊[16]。

(2)自适应交叉操作

交叉操作是指按较大的概率从交配池中选择两个个体，交换两个个体的某个或某些基因，从而形成两个新的个体。这包括交叉概率的定义和交叉算子的选择两个方面。

①交叉概率的定义

根据要进化个体的不同适应度选择不同的交叉概率，适应度高的个体，选择较小的交叉概率；适应度低的个体选择较大的交叉概率。这样，能使交叉概率随适应度自动改变，保护高适应度的对应的解尽可能地进入下一代。同时，对于种群中各个体适应度趋于一致或趋于局部最优时，有较大交叉概率，避免进入局部最优。定义交叉概率函数如下：

其中，pc1和pc2取(0,1)之间的合适的值，一般取pc1为0.9，pc2为 0.6。确定交叉概率 pc后，由系统产生随机数r，若 r＜pc，则交叉。

②交叉算子

交叉算子是遗传算法区别于其它进化算法的重要特征，它在遗传算法中起关键作用，是产生新个体的主要方法，决定了遗传算法的全局搜索能力。本文引入一种新的前置交叉遗传算子，其中两父串相同时仍能产生新的个体，这样削弱了对群体多样性的要求，能够有效地避免传统遗传算法“早熟收敛”的缺点，在实验中也显示了优良的效果。其操作如下：任意给定两个染色体A和B，首先在A和B中分别随机地产生两个交叉点，然后将每个染色体的交叉段移到对方染色体的首部得到染色体A1和B1，最后后消去相同项得到两个新个体A2和B2。图1可说明其操作过程，并且可看出，当染色体相同时，该交叉算子仍然可以产生不同于父体的新个体，从而有效地克服“早熟收敛”的缺点。

图1 交叉方式示例

(3)自适应变异操作

变异操作是指以较小的概率将染色体中的某些基因值用其他可能的基因值来替换，从而形成新的个体。变异操作用来维持群体的多样性，防止出现早熟现象。本文同时采用2-OPT法和2-Exchange法进行变异操作。其中，2-OPT法是指任取同一子路径上的两个客户点i和j互换位置；2-Exchange法是对2-OPT法的扩展，指从不同的两条子路径中分别选取两个客户点i和j互换位置。变异概率按如下公式确定：

其中，pm1和 pm2取(0,1)之间的合适的值，一般取pm1为0.1，pm2为0.001。确定变异概率pm后，由系统产生随机数r，若r＜pm，则发生变异。

第五步，用C-W节约启发式算法优化子路径。

遗传算法是一种全局优化算法，其局部搜索能力较弱，而C-W节约启发式算法则具有较强的局部搜索能力。C-W节约启发式算法的基本思想是首先把各个客户单独与车场相连，构成m条“0-i-0”(i=1,2,…,m)初始化线路，第i条线路的运输距离为ci0；然后把客户i和客户j连接在一起，形成线路“0-i-j-0”(i,j=1,2,…,m)，计算连接后的距离节约值：

s(i,j)越大，则客说明把客户i和客户j连接在一起时总距离节约值越多，因此应优先连接s(i,j)值大的点i和点j，如此根据节约值的大小，将所要服务的客户依次连入行车路线，使问题得到解决。

第六步，算法终止判断。

若算法执行了最大进化代数，则终止，选择性能最好的染色体所对应的路径集合作为原VRP问题的优化解输出，否则返回第二步。

3 实验结果及分析

为验证算法的有效性，本文采用C++语言对上述混合遗传算法(VPHAGA)编制了求解程序，并从VRP基准测试实例中随机选取10例进行了计算(基准测试实例可从网址http://branchandcut.org/VRP/data下载得到)，实例相关描述见表1，每例实例均计算20次；本文设定的初始种群规模为40；同时，本文对文献[4]介绍的结合2-opt局部优化算法的GA with 2-opt及文献[8]所介绍的改进交叉算子的NGA对该10例实例也分别计算20次，参数设置与文献[4]和文献[8]完全一致(选择文献[4]和文献[8]所介绍的算法进行对比的原因是这两个文献的计算结果较好，具有一定的代表性)；三种算法的最大迭代次数设定为1000次，计算结果如表2所示。

表2 三种算法对10个测试实例的20次计算结果

由表2可以看出，本文设计的变种群规模混合自适应遗传算法在随机选取的10个实例上的计算结果均优于文献[4]和文献[8]方法所得的解。在前5例实例中VPHAGA均能找到已知最好解；在后5例实例的计算中，虽然20次的运算没有达到已知最好解，但结果与已知最好解的差距非常微小，相对误差最大的是对大规模实例F-n135-k7的求解结果，但误差也仅为2.32%。这说明本文设计的算法的寻优能力是有效的。

为测试算法的稳定性，表2给出了20次计算中求得的解的平均值、最差值和标准差。从表2中可以看出，本文算法求解的平均值及最差值也均优于文献[4]及文献[8]所介绍的方法；除实例P-n76-k5，本文算法的标准差均小于文献[4]及文献[8]中方法计算得到的标准差，这一结果表明利用本文设计的算法求解VRP是稳定的。另外还可以看到，随着实例规模的增大，VPHAGA的求解标准差并没有明显增大的趋势，这表明该算法对大规模问题的求解也较为稳定，具有一定的普适性。

4 结束语

本文设计了一种求解VRP的变种群规模混合自适应遗传算法。首先，引入一种与进化代数和适应度值相关的变种群规模函数来控制种群规模的变化；然后，利用改进的自适应交叉概率函数和变异概率函数动态调整交叉概率和变异概率，这种交叉概率函数及变异概率函数均随个体适应度值的变化而发生改变。为改善遗传算法局部搜索能力差的弱点，本文在对染色体进行遗传操作后，应用C-W节约启发式算法对生成的子路径进行进一步的优化，充分将遗传算法的全局搜索能力与节约算法的局部搜索能力有机地结合在一起，做到优势互补。为证明该算法的有效性，本文从VRP基准测试实例中随机选取10例进行了计算，并与已有文献进行了对比分析，结果表明本文设计的算法具有更好的寻优能力及稳定性，且对大规模VRP问题仍具有良好的性能。

[1] 李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京:中国物资出版社,2001.

[2] Toth,Paolo,Vigo.Exact Algorithm for the Vehicle Routing Problem with Backhauls[J].Transportation Science,1997,31(4).

[3] 周明,孙树东.遗传算法原理及应用[M].北京：国防工业出版社,2002.

[4] 汪祖柱,程家兴,方宏兵等.车辆路径问题的混合优化算法[J].运筹与管理,2004,13(6).

[5] Goldberg D E.Optimal Initial Popolation Size for Binary-Coded Genetic Algorithms[R].TCGA Report No.85001,Tuscaloosa,University of Alabama,1985.

[6] Goldberg D E.Sizing Populations for Serial and Parallel Genetic Algorithms[A].Proceedings of the 3rd International Conference on Genetic Algorithms[C].Morgan Kaufmann Publishers,San Mateo,CA,1989.

[7] Arabas J,Michalewics Z,Mulawka J.Gavaps-A Genetic Algorithm with Varing Population Size[A].Proceedings of the First IEEE International Conference on Evolutionary Computation[C].IEEE Service Center,Piscataway,NJ,1994.

[8] 张丽萍,柴跃廷.车辆路径问题的改进遗传算法[J].系统工程理论与实践,2002,(8).