基于HMM的中国股市状态转换及预测

胡淑兰，魏 捷，黄 晟

（中南财经政法大学 统计与数学学院，武汉 430073）

0 引言

在股票市场中，大家最关心的股市状态，是涨，还是跌，或是震荡徘徊，而股票的价格深受到政治、经济等各方面的因素影响，影响的程度和信息并不完全透明。常说“股市有风险，入市需谨慎”，股市的风险指的是这些不确定性因素，如政策、利率、汇率、通货膨胀率、所属行业规划、个人因素等各种随机因素，这些也都会导致股市状态的瞬间转换。由于惯性原理和政治经济发展的趋势，这样的状态转换也具有一定的随机规律性。这样的随机规律性往往具有离散性、无后效性和稳定性等特点，则可以与马尔科夫模型或马尔科夫模型的某种函数形式相拟合。

1 数据的描述性统计

1.1 数据来源及处理

本文研究的股价指数来源于上海证券交易所，将最新的数据加入到研究对象中，时间选取2000年7月到2011年6月，以每月月底收盘价为代表，共计132个数据。

股指（Index）一般选取以日为单位的金融序列分析，但容易出现非平稳的现象，股指的统计特征也会随时间变化而呈现出不稳定性，所以本文尝试选取月度股指数据做股市波动研究对其平稳性进行检验。

首先对月度数据进行初步处理，相对估值st1=[(indext/indext-1)-1]×100 得 到 ST序列，表示如图1。

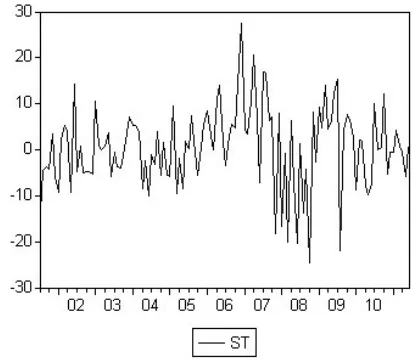
图1

对相对估值序列的平稳性进行检验，由上图可知ST序列无趋势项且具有常数项，所以运用 ADF-Test的（C，0,0）模式进行检验，数据平稳性检验结果（表1）显示ST序列存在单位根不平稳。但该结论并非经常有效，ST序列图形现实只是在2006～2008年存在大幅度的震荡，属于大的结构突变，此后趋势逐渐回稳。

表1 数据平稳性检测

1.2 偏度和峰度检验

偏度Skewness和峰度Kurtosis是用来分析总体数据对均值的偏离状况，具体表示为：

偏度用正负来决定整体分布的左右偏离，绝对值的大小来决定偏离的程度。而峰度的正负（kurtosis≥≤3）用来决定整体分布的高和矮。如下表，描述统计结果显示出深市的相对股票指数波动是剧烈的，可见并非正态分布或渐近正态分布。

表2 描述统计

1.3 移动标准差分析结果

由图2的移动标准差的结果。从2000年6月开始，以每连续12个数据作为标准差统计，得到108个数据。在2002年至今，只在2007年下半年到2009年上半年区间，其标准差大于10。在2006年下半年，波动性突然增强，标准差开始急剧上升。在2006～2009年股市的强波动性，也充分体现2008年全球金融危机带来的影响。

图2

2 实证分析及结果

2.1 股市状态的相关定义

按照股市一般最常见的三种状态，将其分为震荡市、熊市和牛市。股市数据的波动只是这三种状态具体的数字体现。为了更好得了解牛市和熊市的涨跌的程度，可将三种状态细化成五种状态，如下定义为：

S1=2大（疯）牛市，S2=1成长市，

S3=0震荡市，S4=-1弱熊市，

S5=-2大（疯）熊市

S1代表大牛市，体现为股价指数急剧上升，本文将超出了同期的GDP上涨速度的月上升幅度视为大牛市。（考虑到当期GDP增长率以使对状态的界定更具可比性）

S2代表成长市，体现为股价指数以较缓和的速度上升，本文界定月变化幅度在小于同期GDP增长率而大于2.5%为成长市。

S3代表震荡市，体现为股价指数在较小范围内波动，可视为“横盘”，本文将变化幅度在2.5%以内的月份视为震荡市月（我国一年定期存款利率常在2.5%左右，故选取2.5%为分界点）。

S4代表弱熊市，与成长市相对应。

S5代表大熊市。与大牛市相对应。

根据上述分类标准，对ST序列进行状态分类得到状态Z，并绘制以下状态图（见图3）。

图3

从图3中可看出，无论是哪种状态，都存在较明显地聚集现象，也可以理解为一种惯性原理。2001到2006年，股指相对较平稳，大牛市和大熊市都较少出现，仅仅在2002年和2003年初偶尔出现。2001年6月27日下跌回调至将近最高点时，股指开始了持续地下跌，之后开始了一轮弱熊市行情。在2002年前期出现过4次反弹整理，随后股指出现持续不断地向下调整，至2002年末跌至谷底。股指运行至2003年，展开一波急速上攻行情后开始在高位平台整理，年中逐步回落后于年末开始了另一波持续的上涨行情，一直持续到2004年初。股指于当年于4月达到顶点后开始进入绵绵阴跌直至2005年下半年，期间虽有数次反弹但持续不久又继续下探。进入2006年至2007年，由于前期跌幅太深而出现的技术性回调，人民币升值、外贸顺差扩大、经济持续快速发展、居民储蓄大幅增加、投资渠道单一，基金业迅速发展，股权分置改革的基本完成等多种因素，股市不断上涨，出现多个大牛市。此次牛市延续到2007年末，出现大熊市，至2008年初，由于货币政策从“紧”到“松”，及后来出现的国际金融危机及股市自身调整，股指跌破了牛市支撑位，此后，大熊市频现，市场出现恐慌性抛盘。进入2009年，为对抗金融危机，货币政策又从“紧”到“松”，新发行货币增加，且积极的财政政策效用显现，整个2009年基本处于不断地上涨中。从2010年开始，货币流动性开始主导了A股走势，又因欧洲债务等危机不断蔓延的外因和国内政策环境变化，2010年至今，股指几乎一直处于不断震荡中，形成了多个震荡市。

2.2 隐藏马尔科夫模型（简称HMM）模型

如果一个随机过程的将来状态只依赖于现在的状态，却不依赖于过去的状态，则称该随机过程具有马尔科夫性，或称此过程为马尔科夫过程。当时间和状态都是离散时，我们称马尔科夫过程为马尔可夫链。隐藏马尔科夫模型最初是由Baum和Pietre将其作为马尔可夫链的某种函数形式而提出来的，故也可以看成一个双重随机过程,由马尔可夫链和一般随机过程两个部分组成。马尔可夫链的部分是用来描述状态的转移，用转移概率描述。一般随机过程的部分是用来描述状态与观察序列间的关系，用观察值概率描述。之所以称为HMM模型（“隐藏”马尔可夫模型），因为它的状态转换的过程是不可观察的。HMM定义如下：

(1)S={S1,S2,...,SN}代表一组状态的集合，状态数为N，并用Xt来表示t时刻的状态。

(2)Y={Y1,Y2,...,YM}代表一组可观察序列的集合，M是从每一状态可能输出的不同的观察值的数目。

(3)qij=P{Xi+1=Sj|Xt=Si},1＜i,j≤N表示状态转移概率分布。

(4)状态Sj的观察概率分布B={bSj(Yk)}，表示状态j输出相应观察值的概率，其中

bSj(Yk)=P{yt=Yk|Xt=Sj},1≤j≤N,1≤k≤M

(5)初始化状态分布 π={πi}，πi=P{X1=Si},1≤i≤N。

由上可知，HMM是定义在S×Y空间上的随机过程，换言之，HMM是由五元变量组λ：λ=(S,Y,π,Q,B)来定义的。如果状态和观察值序列给定时，HMM或简写为λ=(π,Q,B)来定义。

2.3 基于HMM的股票指数模型

结合前面介绍的隐藏马尔科夫模型的建模知识，根据股票指数的数据，设定如下模型：

Xt——随机变量，表示时间t时股指所处状态；

t——单位时间，t=1,2,3…；

S——状态集合，S={S1,S2,S3,S4,S5}，股市最后发展的状态为成长市，S2为最佳，因为其能够适应经济不断发展，股市正向合理波动与经济发展速度相对应；

状态转移矩阵：利用Markov过程来分析相对股指的变化趋势，用状态转移矩阵来表示各种状态的转移情况。状态转移矩阵用矩阵Q来表示：

下面将研究对象的132个数据进行状态分类，T表示时间，S表示状态，如2000～2007表示2000年7月，S2表示成长市：

T S T S T S T S T S T S3 S3 S4 S1 S4 S4 S2 S4 S4 S3 S2 S3 S1 S4 S2 S5 S4 S1 S2 S4 S3 S3 00-07 01-01 01-07 02-01 02-07 03-01 03-07 04-01 04-07 05-01 05-07 06-01 06-07 07-01 07-07 08-01 08-07 09-01 09-07 10-01 10-07 11-01 S2 S3 S5 S5 S4 S1 S3 S2 S3 S4 S3 S2 S4 S2 S1 S5 S3 S1 S1 S4 S1 S3 00-08 01-02 01-08 02-02 02-08 03-02 03-08 04-02 04-08 05-02 05-08 06-02 06-08 07-02 07-08 08-02 08-08 09-02 09-08 10-02 10-08 11-02 S3 S4 S4 S2 S3 S3 S4 S2 S4 S2 S2 S2 S3 S2 S1 S3 S5 S2 S5 S3 S3 S2 00-09 01-03 01-09 02-03 02-09 03-03 03-09 04-03 04-09 05-03 05-09 06-03 06-09 07-03 07-09 08-03 08-09 09-03 09-09 10-03 10-09 11-03 S4 S2 S4 S2 S4 S3 S4 S2 S2 S4 S3 S3 S2 S2 S2 S5 S4 S1 S2 S3 S3 S3 00-10 01-04 01-10 02-04 02-10 03-04 03-10 04-04 04-10 05-04 05-10 06-04 06-10 07-04 07-10 08-04 08-10 09-04 09-10 10-04 10-10 11-04 00-11 01-05 01-11 02-05 02-11 03-05 03-11 04-05 04-11 05-05 05-11 06-05 06-11 07-05 07-11 08-05 08-11 09-05 09-11 10-05 10-11 11-05 S2 S3 S4 S2 S4 S3 S3 S4 S4 S3 S4 S2 S2 S1 S2 S2 S5 S2 S2 S4 S1 S3 S2 S2 S3 S5 S4 S2 S2 S3 S3 S4 S3 S1 S1 S2 S5 S4 S2 S2 S2 S5 S4 S4 00-12 01-06 01-12 02-06 02-12 03-06 03-12 04-06 04-12 05-06 05-12 06-06 06-12 07-06 07-12 08-06 08-12 09-06 09-12 10-06 10-12 11-06 S

表3 2000～2011年上证指数不同状态数

由表3可看出，2000～2011年上证指数共经历大熊市的状态有10个月，弱熊市状态34个月，震荡市状态33个月，成长市状态42个月，大牛市状态13个月。每个月状态Xk在S1,……,S5状态之间的转移概率为qij=P(Xk+1=Sj|Xk=Si)。通过132个月的状态数据计算，可以确定股市状态间的转移概率矩阵：

2.4 结果分析及总结

上面的概率转移矩阵表明中国股票市场的波动性还是比较大的，因为矩阵的对角线都小于0.5，也就是说前一个月的股市状已知时，下个月的股市状态发生转移的概率较大，换言之，股市状态的稳定性较差，这就体现了中国股市发展不够均衡和平稳。准确地来看，如果初始状态是大牛市，那么继续向大牛市或成长市转移的概率为0.214+0.357=0.571，这说明大牛市的惯性还是很大的，股民继续维持盈利的可能性也较大。如果初始状态是成长市，那么继续维持成长市的概率为0.425，相对其他状态，可能性也还是比较大的。当然这与我国股民的“从众”心态和“买涨不买跌”的投资心理有很大的关系。如果初始状态是大熊市，维持大熊市的概率为0，而向弱熊市转移的概率为0.272，向成长市转移的概率为0.455，这充分说明，大熊市很难一直维持，而且向成长市调整的可能性很大。如果初始状态是弱熊市，则向震荡市转移的概率是0.424，停留在震荡市的概率是0.243。如果初始状态是震荡市，维持震荡市的概率是0.235，向成长市转移的概率是0.265，向弱熊市转移的概率是0.382。

目前有很多学者专家对股市及相关资本市场做了很深入的研究，但是都必须有一些理想的或假设的前提条件，因为各个诱因之间相互影响，并不断地发生变化，研究的结果也各式各样。本文采用了隐藏马尔科夫模型的隐藏状态的概率转移矩阵的计算方法，细分了股市的三种状态为五种状态，将10年来的数据作为样本系统分析了股市在

这五种状态之间的变换的规律性。从研究结果来看，由于经济发展不够均衡，投资者心理不够成熟，出现明显的惯性及羊群现象。同时，随着金融及相关国家政策逐渐健康、完善，股市状态波动逐渐会趋于平缓，并以成长市为主导股市状态，股市就会逐步进入稳定平衡发展的阶段。

[1] 龚光鲁,钱敏平.应用随机过程教程及在算法和智能计算中的随机模型[M].北京：清华大学出版社，2004.

[2] 李占风.经济计量学[M].北京：中国统计出版社，2010．

[3] 朱建平：经济预测与决策[M].厦门：厦门大学出版社，2007．