一维准晶体III型切口的应力与位移
2011-07-23巫建清施伟辰
巫建清,施伟辰
(上海海事大学物流工程学院,上海 201306)
0 引言
准晶体被发现于1984年,其晶格点阵呈现准周期性,即晶格结构存在局部重新排列现象.在外载荷的作用下,准晶体的宏观力学特性随材料内部结构的改变而变化.[1]由于准晶体的应变能密度为标量,而且准晶体中存在使晶格局部重排的相位子场的位移和应力,因而在应变能密度形式不变的点群操作中可获得多种反映其材料特性的材料系数.[2]对于准晶的裂纹问题,已有一些研究[3-4],但针对V型切口问题的研究相当少.本文由一维准晶的III型问题[5-6]出发,以解析函数的方法分析研究该材料III型切口问题的应力和位移,给出其围绕切口尖端的分布,然后讨论其切口尖端处的J积分.
1 一维准晶基本方程
由文献[7]给出的一维准晶二次不变量,可得一维准晶的应变能密度
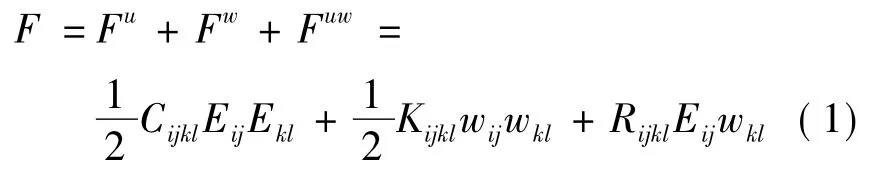
再由广义Hooke定律
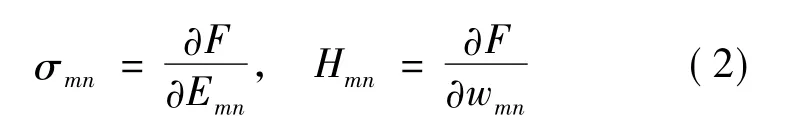
可推导得出本构方程(见附录).考虑III型问题,令u1=u2=0,u3=u3(x1,x2),w3=w3(x1,x2),代入总体本构方程(见附录)中,可得到III型问题的本构方程:
Laue类5,7和9

Laue类8

式中:u3和w3分别为声子场和相位子场在z方向上的位移;C44和K2分别为声子场和相位子场的弹性常数;R3和R4分别为声子场和相位子场的弹性耦合系数.
将式(3)和(4)分别代入平衡微分方程σ3i,i=0和 H3i,i=0 中,均有▽2u3=0,▽2w3=0.由于解析函数的实部和虚部均为调和函数,可令
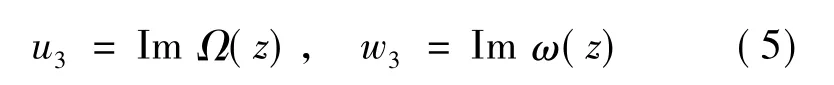
式中:Ω(z)和ω(z)为关于z的解析函数;z=x1+ix2.将式(5)代入式(3)和(4)后,应力可表示为Laue类5,7和9
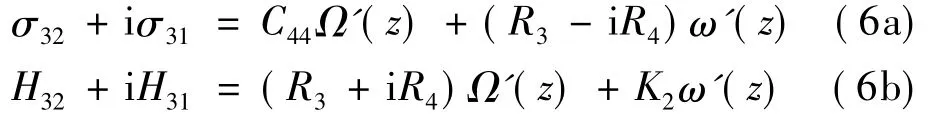
Laue类8
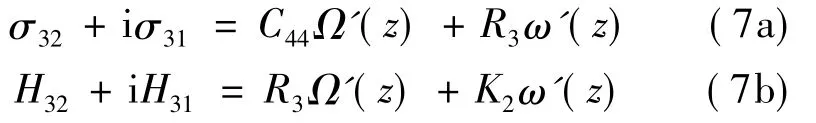
直角坐标系与极坐标系下的应力转化公式为
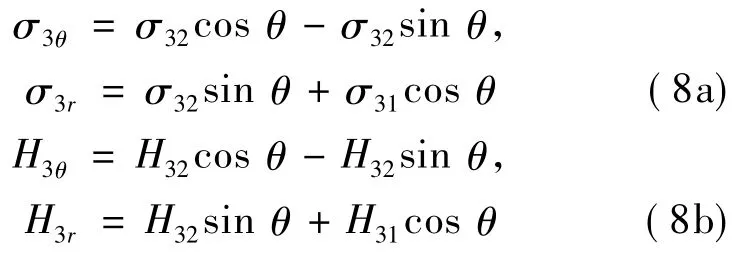
将式(6)和(7)分别代入式(8)中,得极坐标系下的应力形式:
Laue类5,7和9
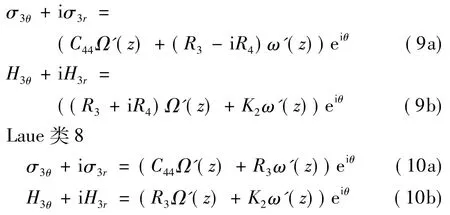
2 切口问题
研究准晶III型切口的应力奇异性,见图1.

图1 准晶III型切口
切口面剪切应力为零,边界条件表示为

假设
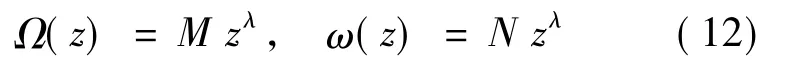
将式(12)代入式(9a),(9b),(10a)和(10b)后,得Laue类5,7和9
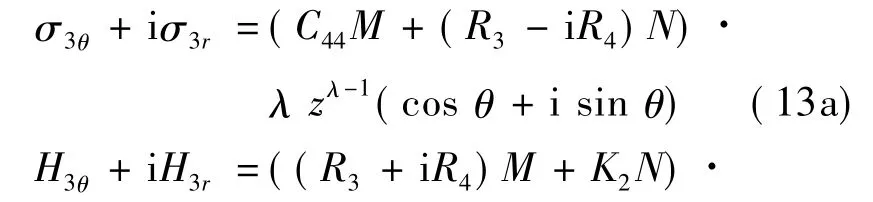
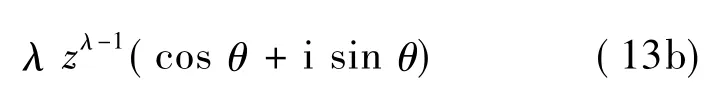
Laue类8

由于M和N可为任意复数,对Laue类5,7和9,可取

对Laue类8,可取
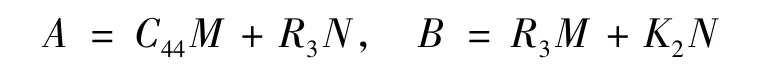
式中:A和B 为任意复数.令z=reiθ,则Laue类5,7,8和9中应力可取统一表示形式:

令 A=A1+iA2,B=B1+iB2,由式(5)可得位移为Laue类5,7和9
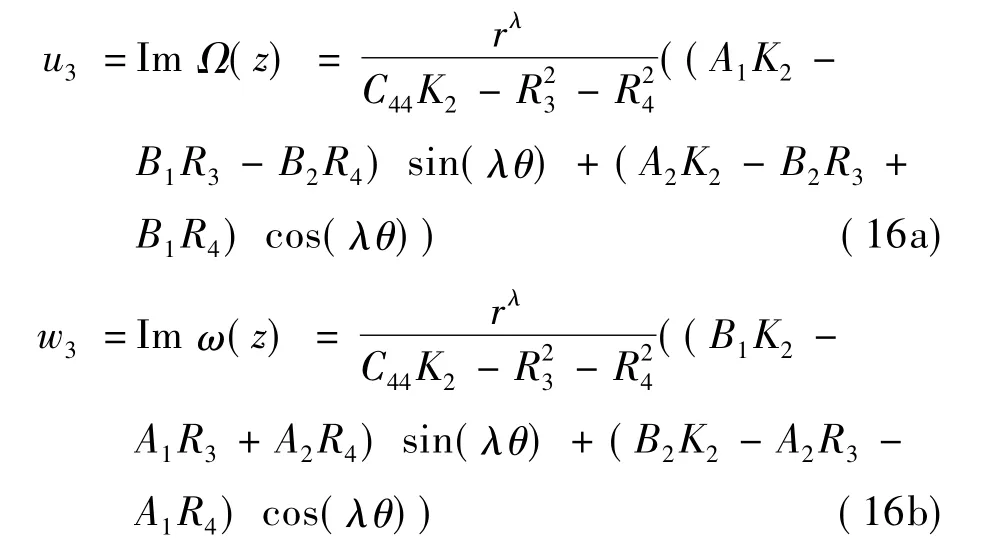
Laue类8
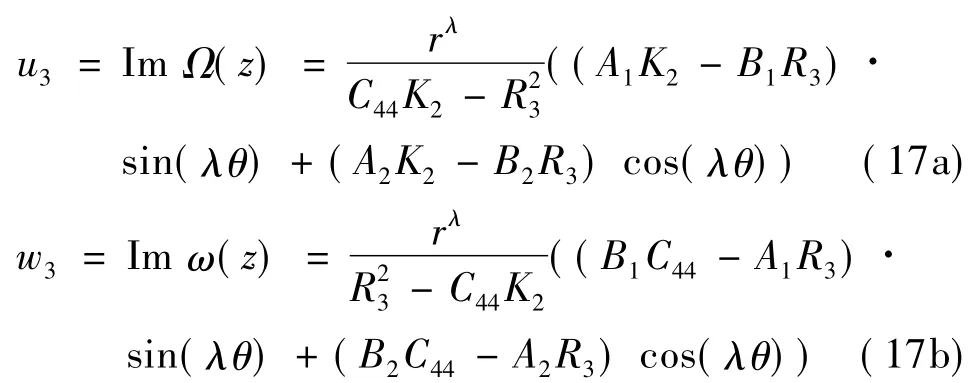
将式(15)代入边界条件式(11)中,有

将两个方程组展开后,实部和虚部分开,写成矩阵形式有
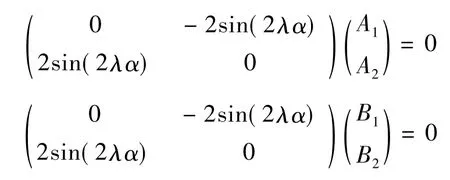
由于A和B为任意复数,要使A和B有非零解,系数矩阵的行列式必须为零,即

则有

切口尖端位移为有限值时,则可求得
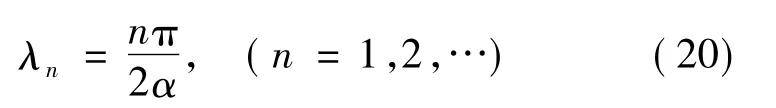
将式(20)代入式(15)中,可得应力为
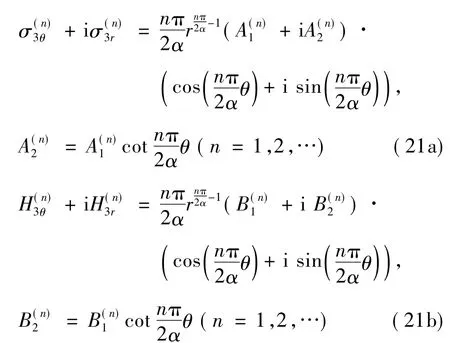
引入切口应力强度因子[8-9]
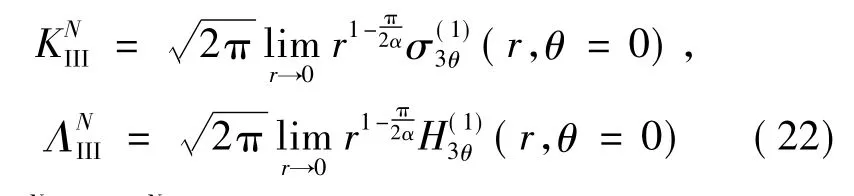
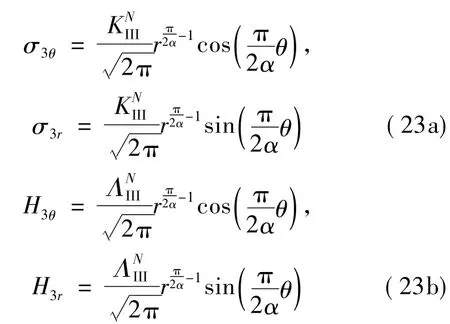
其中
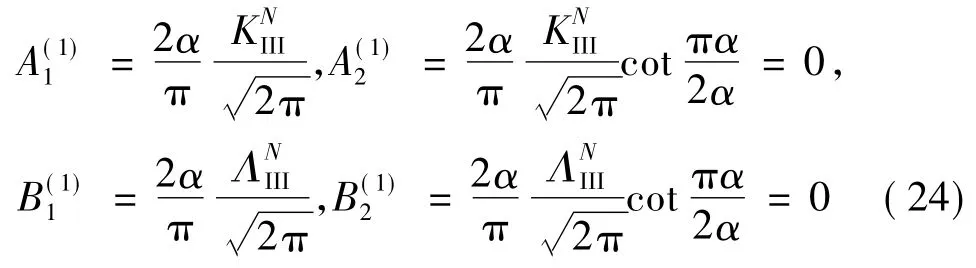
将式(20),(22)和(24)代入式(16)和(17)可得位移:
Laue类5,7和9
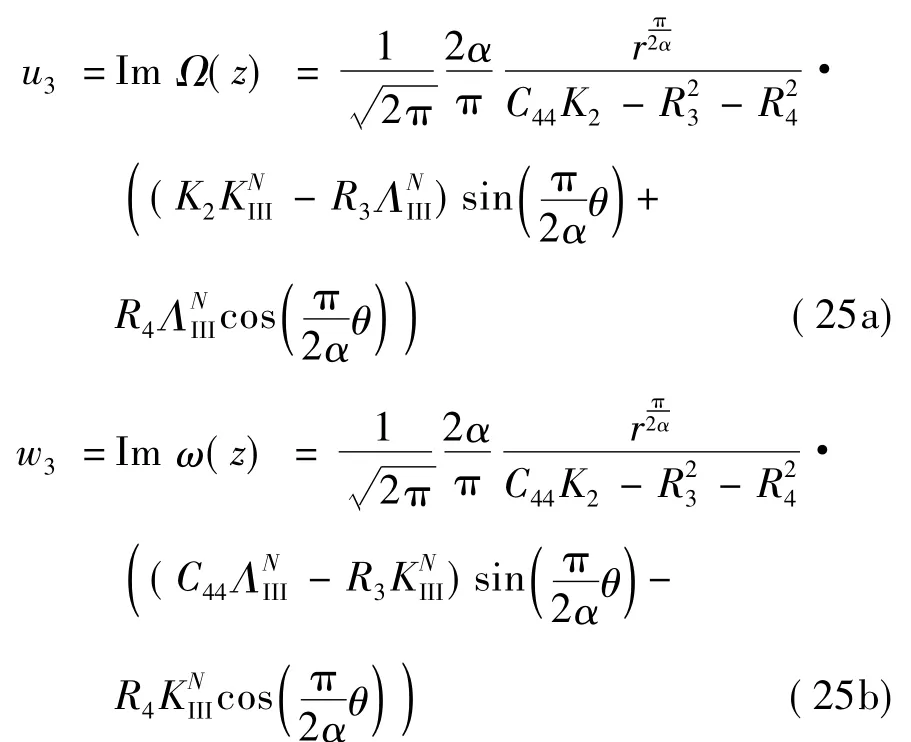
Laue类8

3 J积分
将文献[10-11]中的J积分
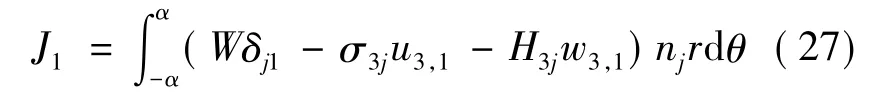
用于切口问题,其积分路线取围绕切口尖端的圆周路径,见图2.
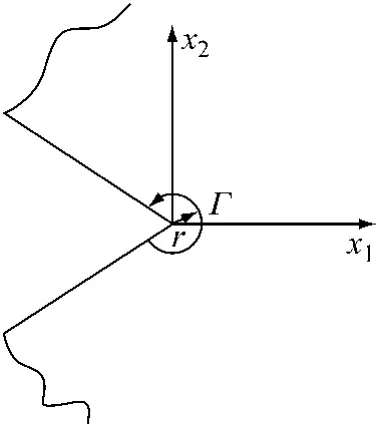
图2 切口问题积分路径
式(27)中:W为应变能密度;δj1为克罗内克函数.线性材料III型问题的应变能密度[11]可表示为
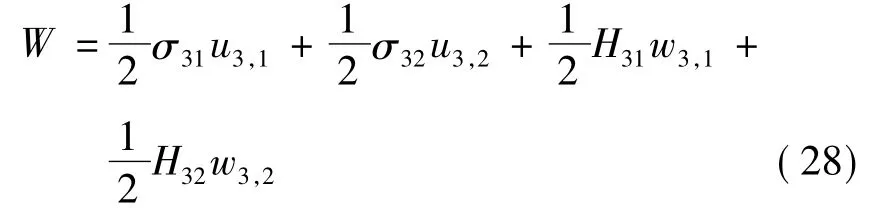
将式(23),(25),(26)和(28)代入式(27),经计算可得
Laue类5,7和9
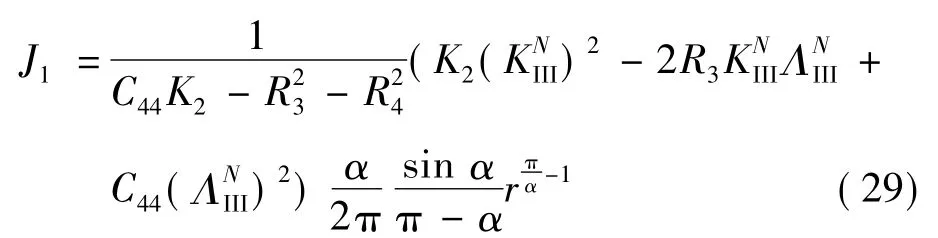
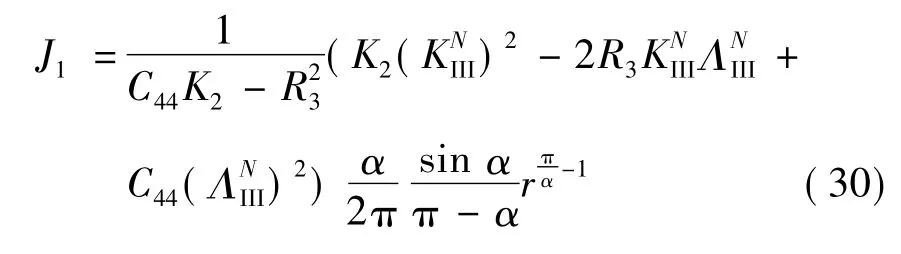
Laue类8比较式(25),(26),(29)和(30)可知,尽管 Laue类5,7和9位移中出现项,与一般晶体和Laue类8均不相同,但是在J积分中并未出现.对于切口问题π/2<α<π,从而当r→0时,J→0,这和一般弹性体一样;另外,当α→π时,J积分变为裂纹开裂的能量释放率:
Laue类5,7和9
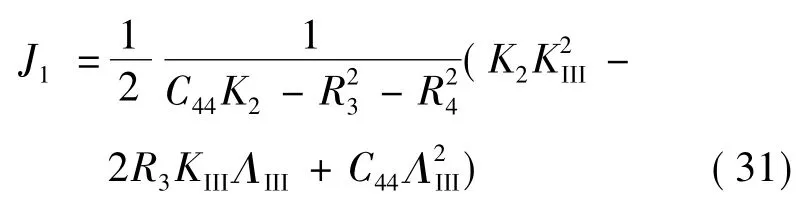
Laue类8
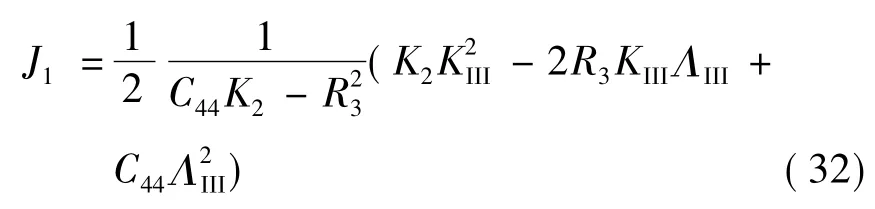
同样可见,Laue类8与Laue类5,7和9的能量释放率的数学形式也相同.显然,当无相位子场时,ΛIII=0,式(31)和(32)退化为一般弹性材料的能量释放率形式,与经典力学中结果一致.
4 结束语
由一维准晶基本弹性理论的本构方程,利用解析函数的理论给出基于极坐标系的应力方程.由切口边界条件得出本征方程并求出切口问题的声子场和相位子场应力位移的渐进解,最后引入应力强度因子,给出切口尖端处的应力位移分布,并计算切口尖端的J积分.计算结果表明,声子场和相位子场通过本构方程耦合,切口尖端处声子场和相位子场的位移也具有耦合性,其中Laue类5,7和9的位移与Laue类8的不同,也与一般材料不同,然而J积分仍具有相同的形式.当切口变为裂纹时,J积分给出能量释放率.
[1]DING Dihua,YANG Wenge,HU Chengzheng,et al.Generalized elasticity theory of quasi-crystals[J].Phys Rev,1993(B48):7003-7010.
[2]YANG Wenge,DING Dihua,HU Chengzheng,et al.Group-theoretical derivation of the numbers of independent physical constants of quasi-crystals[J].Phys Rev,1994(B49):12656-12661.
[3]郭玉翠.二维准晶的一个断裂力学解[J].北京邮电大学学报,2001,24(4):53-57.
[4]皮建东,刘官厅,郭怀民.一维六方准晶狭长体中共线裂纹问题的精确解[J].内蒙古师范大学学报,2006(4):391-396.
[5]刘吉军,施伟辰.一维准晶杆的强迫振动[C]//上海市国际工业博览会第三届“工程与振动”科技论坛论文集.北京:中国学术期刊(光盘版)电子杂志社,2005.
[6]刘吉军,施伟辰.一维准晶杆波动过程的d’Alembert解[J].上海海事大学学报,2005,26(1):77-80.
[7]胡承正,杨文革,王仁卉,等.准晶的对称性和物理性质[J].物理学进展,1997,17(4):345-366.
[8]SHI Weichen.Path-independent integral for the sharp V-notch in longitudinal shear problem[J].Int J Solids and Structures,2011,48(3/4):567-572.
[9]SHI Weichen.Collinear periodic cracks and/or rigid line inclusions of antiplane sliding mode in one-dimensional hexagonal quasi-crystal[J].Appl Math and Computation,2009,215(3):1062-1067.
[10]SHI Weichen.Conservation integrals of any quasi-crystal and application[J].Int J Fracture,2007,44(2):61-64.
[11]SHI Weichen.Conservation laws of a decagonal quasi-crystal in elastodynamics[J].Eur J Mech,A/Solids,2005,24(2):217-226.
[12]SHI Weichen,LI Huanhuan,GAO Qinghai.Interfacial cracks of anti-plane sliding mode between usual elastic material and quasi-crystal[J].Key Eng Mat,2007(340/341):453-458.
附录 一维准晶各Laue类本构方程
Laue类5
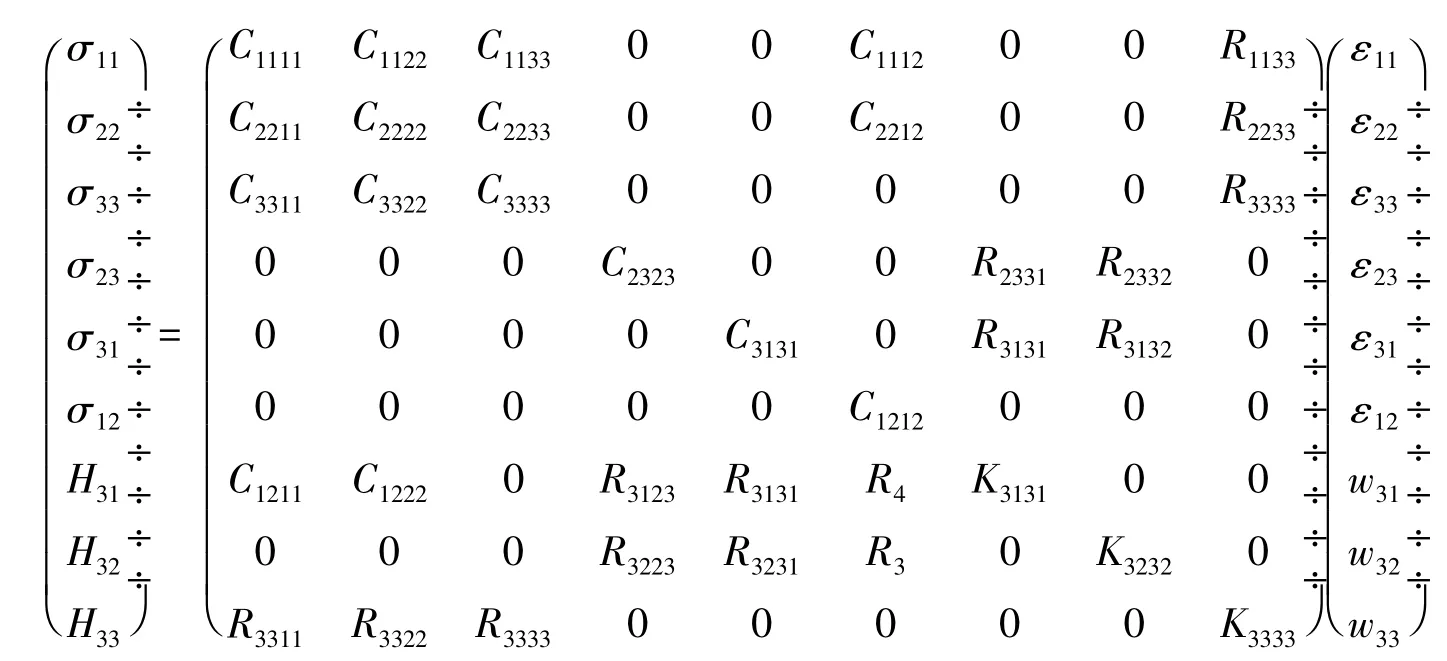
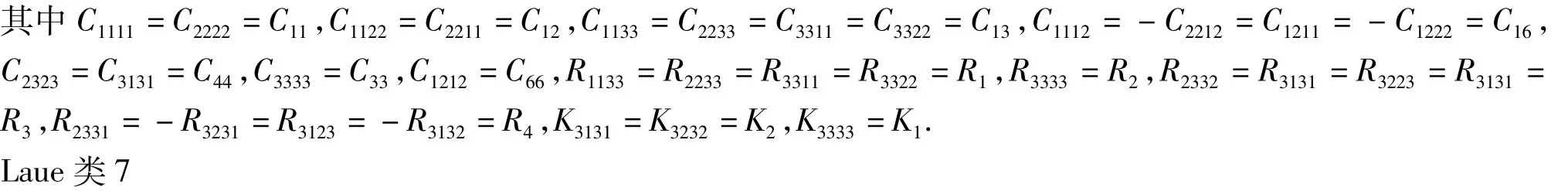
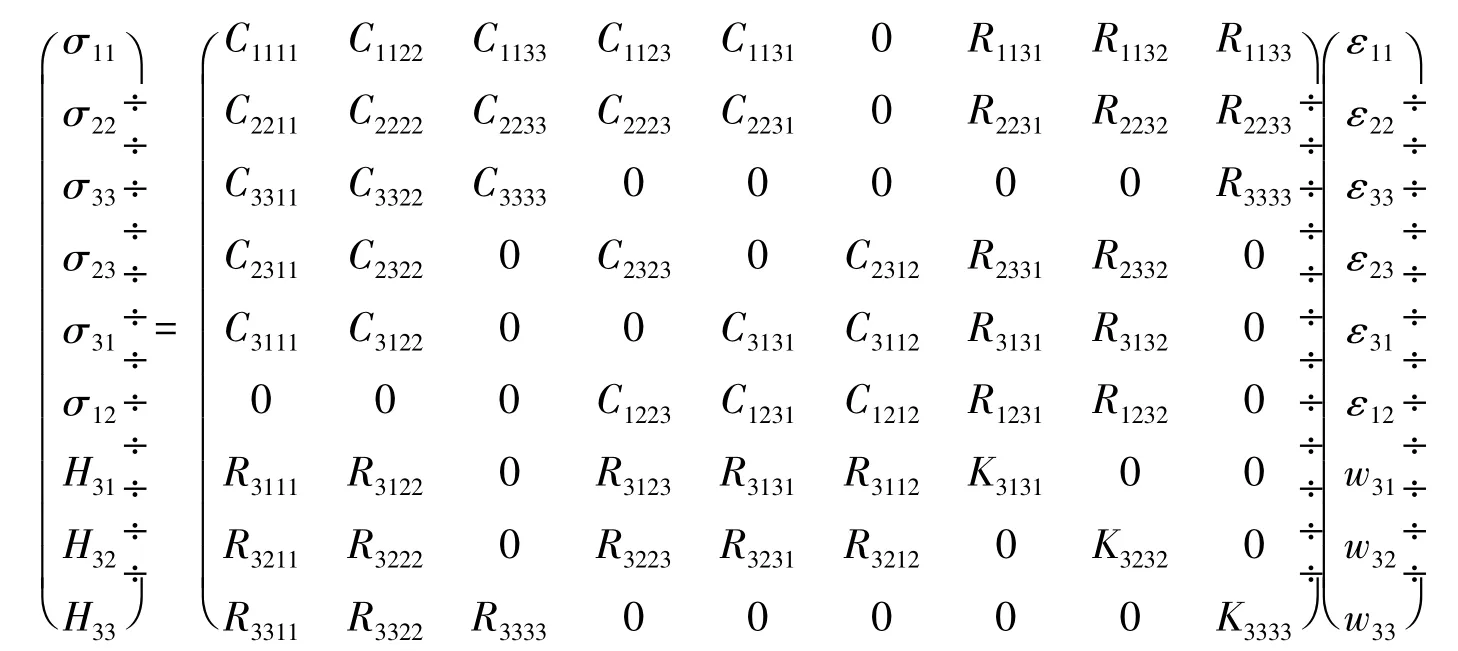
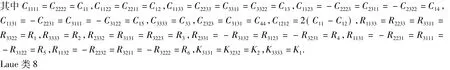
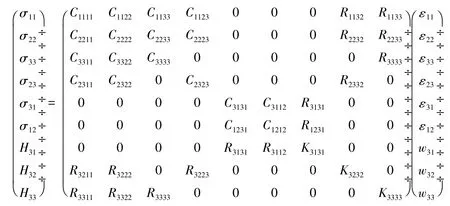
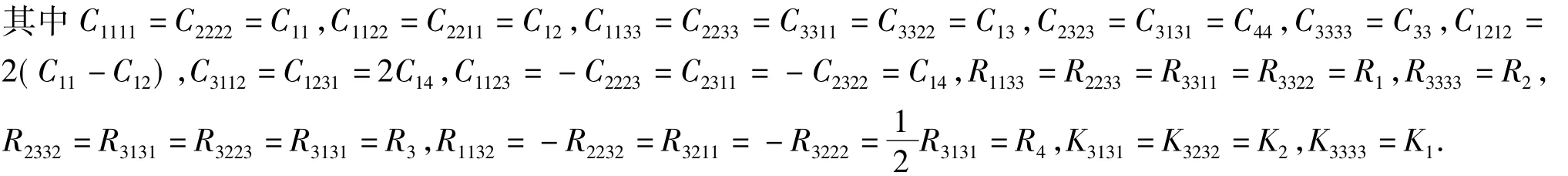
Laue类9

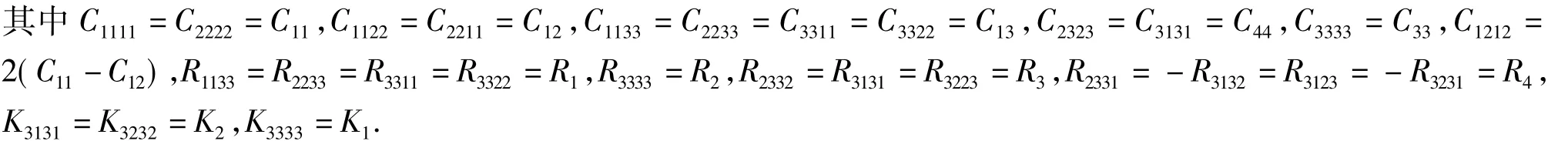
方程中σij和εij分别是声子场应力和应变,Hij和wij分别是相位子场应力和应变.
