简谐环形荷载作用下饱和土体中圆形衬砌隧洞的动力响应研究

黄晓吉，扶明福，徐 斌，黎剑华

(1. 华东交通大学土木建筑学院，南昌 330013;2. 南昌大学建筑工程学院，南昌 330031;3. 南昌工程学院土木工程系，南昌 330099)

Biot 建立饱和土的波动理论以来，后续学者在此基础上对饱和土的动力响应开展了大量研究。Kumar等［1］分析了饱和介质中圆形隧洞在变荷载作用下的径向位移，并推导出脉冲荷载作用下的封闭形式解。通过Laplace 变换，文献［2］分析了轴对称荷载和流体压力作用下饱和介质中圆形隧洞的动力响应，得到了无限弹性饱和介质中圆形孔洞动力响应的解答。文献［4］假设衬砌为完全柔性，分析了平面应变条件下轴对称简谐荷载和简谐内水压力两种荷载作用下的动力响应。文献［5］通过引入Carcione 的黏弹性本构方程，研究饱和多孔介质中圆柱孔洞在衬砌表面作用轴对称简谐荷载和流体压力平面应变条件下的频域响应问题，分析了衬砌和饱和介质的相对刚度及其他因素对动力响应幅值的影响;谢康和等［3］分别考虑衬砌材料为多孔弹性、柔性及刚性介质，研究了黏弹性饱和土体中半封闭圆形隧洞在轴对称荷载和流体压力作用下的动力响应，随后文献［6］考虑衬砌材料和土体的多孔性质，利用Laplace 数值变换研究了任意荷载条件下黏弹性饱和土体中半封闭圆形隧洞衬砌—土动力相互作用问题，得到平面应变条件下瞬时移动等响应模式条件下的数值结果，并讨论了衬砌和土体的相对刚度对隧洞动力响应的影响。刘林超等［7］基于连续介质混合物公理和体积分数概念的多孔介质理论模拟圆形隧洞周围的饱和土体，研究平面应变轴对称简谐荷载作用下无衬砌隧道的稳态响应问题，并分析渗透系数、阻尼系数对隧洞动力响应的影响。而文献［8］采用波函数展开法，分析了垂直入射P 波作用下，埋深、衬砌刚度以及入射频率对中、浅埋隧道衬砌内壁环向动应力分布的影响。基于Biot 理论，陆建飞等［9］研究了移动的空间轴对称荷载作用下饱和土中无衬砌隧洞的动力响应，并讨论了移动荷载的速度对隧洞动力响应的影响。在此基础上，本文研究饱和土中圆形衬砌隧洞在简谐轴对称荷载作用下的动力响应。在本文中，衬砌视为弹性体，土体视为饱和多孔弹性介质，且考虑土体和孔隙流体的压缩性，引入势函数，结合边界条件和连续条件，通过傅立叶变换得到波数域中的动力响应幅值，最后通过傅立叶的逆变换得到空间域内动力响应幅值的数值解。

1 控制方程

如图1 所示，在饱和土中有一简谐集中环形轴对称荷载作用下的圆形衬砌隧洞，R1与R2分别为隧洞衬砌的内外半径。

1.1 饱和土体的基本方程

假定土体为饱和多孔弹性介质，则饱和土体的本构方程为

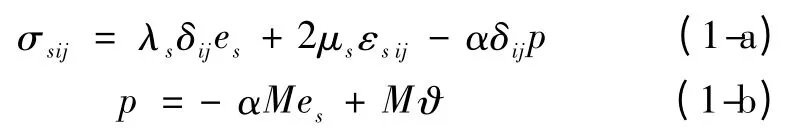
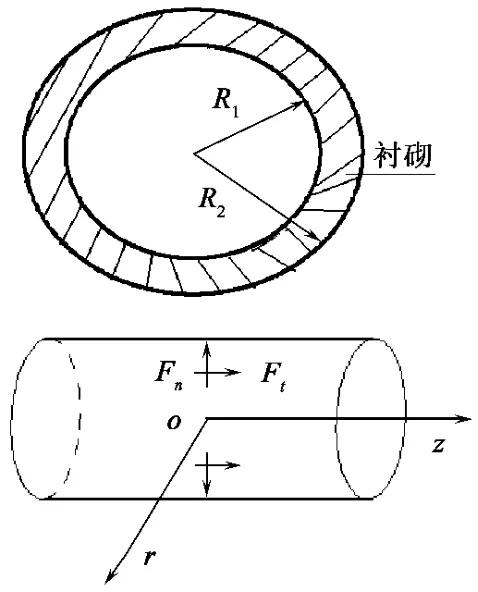
图1 简谐集中环形荷载(Fn = neiωt，Ft = teiωt)作用下的衬砌隧洞的几何模型

式中，σsij，εsij为土体应力和应变张量;δij为克罗奈克符号;es，ϑ 分别为土骨架体积应变和单位体积孔隙水的流体体积增量，es= usi，i，ϑ = - wi，i(usi，wi为土骨架的位移和孔隙水的渗透位移);i，j =1，2，3;p 为孔隙水压力;λs，μs为土体的lame 常数;α，M 为与孔隙水压缩性有关的Biot 参数。

根据Biot 理论，不计体力时饱和土体和孔隙水的运动方程为

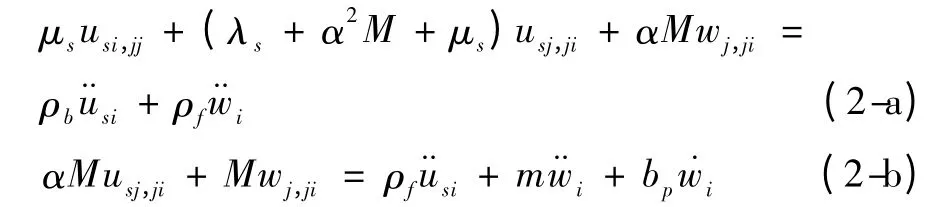
式中，ρb，ρf分别为饱和土体与孔隙水密度;m =a∞ρf/f(a∞为孔隙流体弯曲系数，f 为土体孔隙率);bp= η/k表示土骨架与孔隙流体间的相互作用力(η 为孔隙流体黏性系数，k 孔隙流体的动力渗透系数)。

1.2 衬砌的基本方程

衬砌的本构方程和运动方程分别为

式中，σlij和εlij为衬砌的应力和应变张量;ulij为衬砌的位移(i，j =1，2，3);el= uli，i为衬砌的体积应变;λl、μl为衬砌的lame 常数;ρl为衬砌的密度。

1.3 控制方程求解

在简谐荷载(Fneiωt，Fteiωt)作用且稳态情形下，衬砌隧洞的所有动力响应均有¯feiωt的形式，其中，¯f 表示振幅，ω 表示圆频率。把¯feiωt形式代入运动方程(2)和(4)中，可得

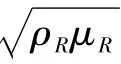
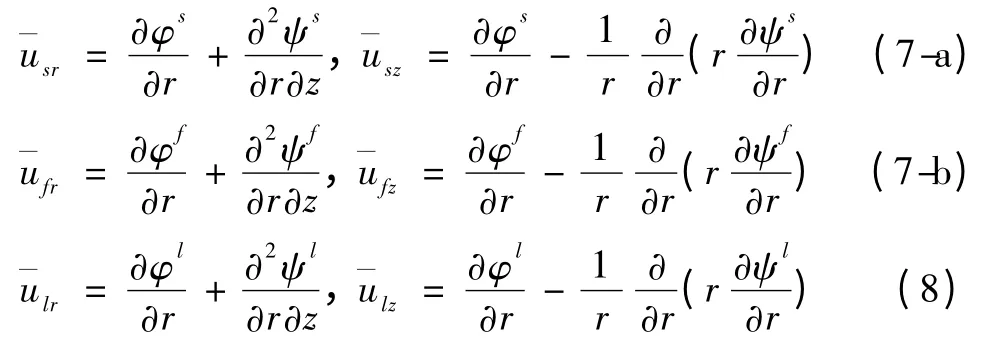
式(7)～式(8)中，下标r，z 为柱坐标系下的r 坐标和z坐标，s，f，l 分别表示土体、孔隙流体和衬砌。

引入势函数后无量纲运动方程转化为柱坐标下的Helmoltz 方程。对Helmoltz 方程进行z→ξ 的傅立叶变换，即可求得波数域中势函数的解答，进而求得动力响应幅值在波数域中的解答。傅立叶正向变换和逆向变换公式如下

式中，上标“∧”表示正向傅立叶变换值。

对Helmoltz 方程进行z→ξ 傅立叶正向变换后，得到波数域中的势函数。考虑到无穷远处饱和土的动力响应趋于零，使γf、γs和γt满足im(γf)＜0、im(γs)＜0，im(γt)＜0，则可求得

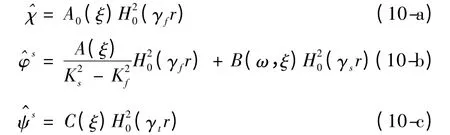
把上述解答代入位移幅值—势函数关系表达式(7)～式(8)，以及饱和土体和衬砌的几何方程和本构方程式(1)和式(3)中，可得土体、孔隙水和衬砌的位移、应力及孔隙水压力在波数域中的幅值表达式。

1.4 边界条件和连续条件

衬砌隧洞的动力响应幅值(位移、孔隙水压和应力)表达式中的7 个待定常数应根据边界条件和连续条件来确定。若圆形衬砌隧洞在简谐集中环形荷载(Fn，Ft)作用下，在衬砌内表面r =R1处应满足

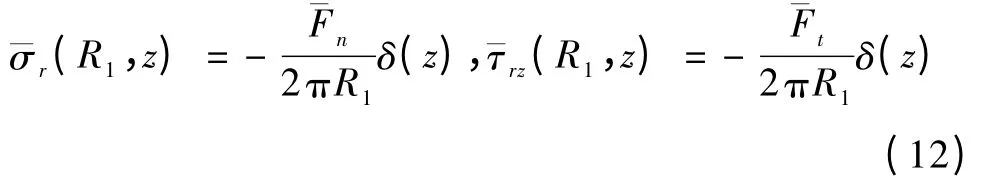
式中，δ()为Dirac—δ 函数。

在饱和土体与衬砌的接触面(r = R2)，若隧洞衬砌完全透水，则孔隙水压

对上述边界条件进行z→ξ 的傅立叶变换，使其转换为波数域中边界条件

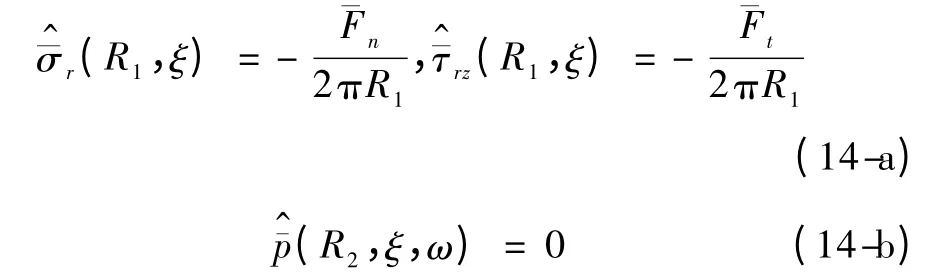
假设衬砌与土体完全接触，则衬砌和土体的应力在接触面(r =R2)处应连续，即

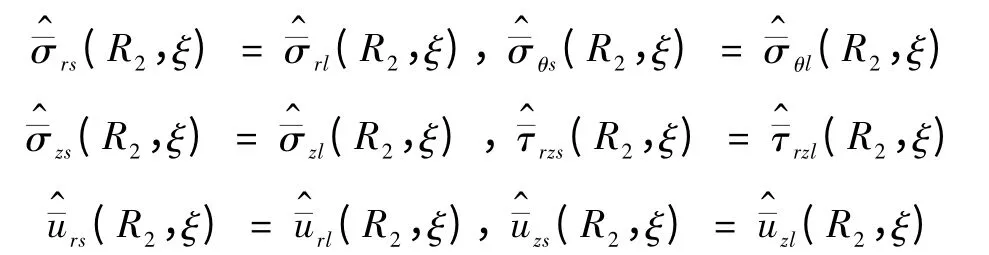
本文引入式(14)中的3 个边界条件及径向、环向正应力与径向、环向位移连续的4 个条件，求得衬砌、饱和土体的位移、应力和孔隙水压力中的7 个待定常数，波数域中应力、位移和孔隙水压幅值得到完全解答。对波数域中的响应幅值进行傅立叶逆变换即可得到空间领域中的应力、位移和孔隙水压幅值。

2 算例和分析

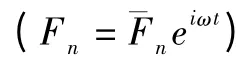
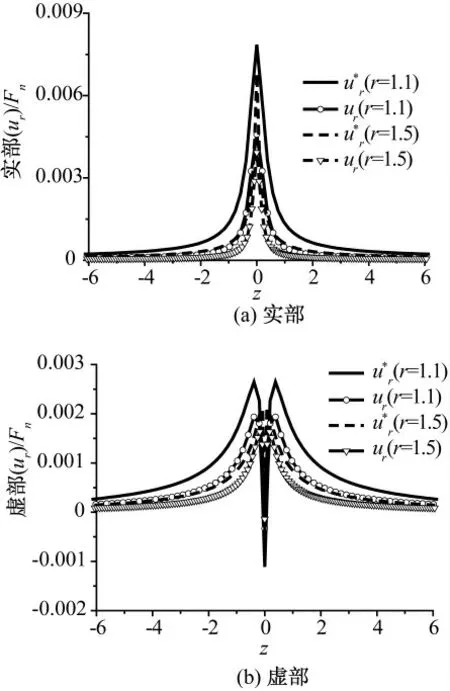
图2 无量纲径向位移幅值实部和虚部曲线

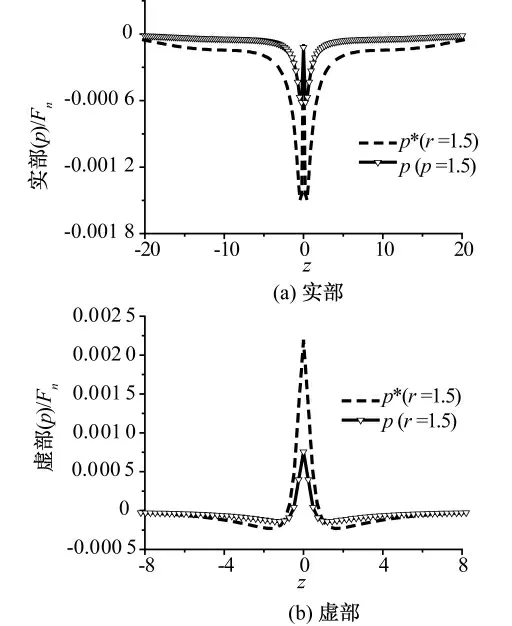
图3 无量纲孔隙水压幅值实部和虚部曲线

从图2、图3 可知，衬砌隧洞和无衬砌隧洞的径向位移和孔隙水压的幅值实部、虚部均对称分布于荷载作用平面的两侧，而z 向位移的幅值实部、虚部则反对称分布于荷载作用平面的两侧。由于衬砌刚度大于饱和土体的刚度，在半径r =1.1 和r =1.5 处，衬砌隧洞的径向位移及z 向位移幅值的最大实部与虚部均小于无衬砌隧洞相应位移幅值的最大实部、虚部。此外，由于辐射阻尼的影响，不管是无衬砌隧洞还是衬砌隧洞，r =1.5 处的径向位移及z 向位移幅值的最大实部与虚部均小于r =1.1 处的径向位移及z 向位移幅值的最大实部与虚部。在半径r =1.5 处，衬砌隧洞外周饱和土中孔隙水压幅值的最大实部、虚部也小于相应位置的无衬砌隧洞孔隙水压幅值的最大实部和虚部。

图4 无量纲剪切应力幅值实部和虚部曲线

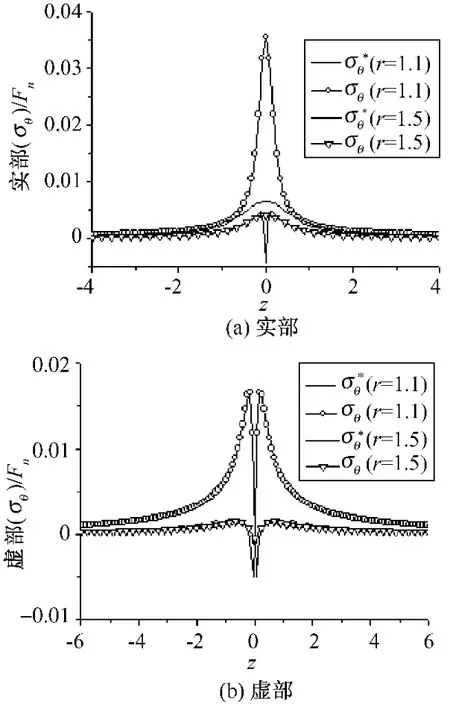
图5 无量纲环向正应力幅值实部和虚部曲线

由图4、图5 可知，隧洞的剪切应力实部、虚部具有反对称性，环向正应力实部、虚部则对称分布于荷载作用平面的两侧。由于衬砌弹性模量远大于外周饱和土体的弹性模量，且衬砌的泊松比小于饱和土的泊松比，在同样压力作用下，衬砌的横向位移远小于饱和土体的横向位移，则衬砌与外周饱和土的界面处存在较大的相对运动趋势;为使两者完全接触，保证两者界面处不存在相互滑移，在衬砌体内产生很大的剪切应力以阻止两者的相对滑移。从图4 可知，在衬砌隧洞r =1.1 处衬砌体内的剪切应力幅值的最大实部、虚部远大于其它三者的剪切应力幅值的最大实部、虚部。由于衬砌体内存在很大的剪切应力，导致衬砌体内产生较大的环向正应力，从图5 可知，隧洞衬砌体内的环向正应力幅值最大实部、虚部均远大于其它三者环向正应力幅值的最大实部、虚部。

3 结语

根据Biot 理论和边界条件，本文研究了简谐集中环向荷载作用下衬砌隧洞的动力响应问题，通过傅立叶变换，得到衬砌隧洞的动力响应解答。根据算例分析的结果可得到如下结论:

1)由于衬砌的刚度大于饱和土的刚度，衬砌隧洞中衬砌内部和外周饱和土的径向位移均比无衬砌隧洞相应处的径向位移小。

2)由于衬砌和外周饱和土弹性模量、泊松比的差异，衬砌内部存在较大的剪切应力及环向正应力。

3)衬砌的存在使得隧洞动力响应的数值和分布发生改变，因此在衬砌隧洞的动力计算中不能忽略衬砌的影响。

［1］KUMAR R.Radial displacements of an infinite liquid saturated porous medium with cylinderical cavity ［J］. Computers and Mathmatics with Applications，1999(37):117-123.

［2］SENJUNTICHAI T，RAJAPAKSE R K N D. Tranisent response of acircular cavity in a porouelastic medium［J］.Int J for Numerical and Analytical Method in Geotechnics，1993(17):357-383.

［3］XIE Kanghe，LIU Ganbin，SHI Zuyuan. Dynamic response of partially sealed circular tunnel in viscoelastic saturated soil［J］.Soil Dynamics ＆ Earthquake Engineering，2004(24):1003-1011.

［4］刘干斌，顿志林，谢康和，等.黏弹性饱和土体中半封闭圆形隧洞的稳态响应分析［J］.中国铁道科学，2004，25(5):78-83.

［5］刘干斌，谢康和，施祖元. 黏弹性饱和多孔介质中圆柱孔洞的频域响应［J］.力学学报，2004，36(5):557-563.

［6］刘干斌，谢康和，施祖元. 黏弹性饱和土体中圆形隧洞动力相互作用［J］.浙江大学学报(工学版)，2005，39(10):194-201.

［7］刘林超，杨骁.基于多孔介质理论的饱和土体中圆形隧洞稳态响应分析［J］.应用力学学报，2009，26(1):12-16.

［8］高广运，李育枢，李天斌. P 波作用下浅埋圆形衬砌隧道动力反应分析［J］.中南公路工程，2007，32(2):56-60.

［9］LU Jianfei，JENG Dongsheng. Dynamic response of a circula tunnel embedded in a saturated poroelastic medium due to a moving load［J］.Journal of Vibration and Acoustics，2006(128):750-756.