舵机用双余度无刷直流电动机设计研究
2011-07-20高金行戴志勇全兴源艾于琛
高金行,戴志勇,全兴源,艾于琛
(西北工业大学,陕西西安710072)
0 引 言
目前,永磁无刷直流电动机已经发展为一项成熟的技术。其以体积小、重量轻、效率高、易于控制颇受业者青睐。随着航空航天技术的不断进步,使得人们对无刷直流伺服电动机的兴趣更为浓厚。本文一改传统有刷直流舵机,根据系统可靠性要求,结合无刷直流电动机电子换向的特点,设计了一种双余度无刷直流舵机伺服电动机。除了上述优越的性能外,它极大地改善了系统运行的可靠性,对未来的军用机载舵机随动系统具有非常重要的实用价值。通过样机性能测试,余度换向优越,系统运行良好,完全满足使用要求。本文对电动机的数学建模、性能仿真作了详细论述,对余度换向技术及调试关键进行了重点分析和讨论,经过对样机性能的综合测试,验证了设计、仿真的准确性。
1 双余度无刷直流电动机原理
本文采用的双余度稀土永磁无刷直流电动机,如图1所示,每个余度电机由两个在空间上互差30°电角度、Y形连接的三相定子绕组和一个共用的稀土永磁转子组成。两套绕组关系如图2所示。绕组电气隔离、磁场耦合,彼此存在互感。
控制时采用120°PWM脉宽调制驱动,两套绕组在电气上彼此隔离,各有一套电气彼此隔离的逆变器单独供电。其中,一套绕组滞后另一套绕组30°电角度。控制该绕组的逆变器也滞后于相应的逆变器30°电角度。两个余度在0°~360°电角度内的触发导通关系如表1所示,其磁场的关系在两个余度分别独立工作时与双余度合成工作时的示意图如图3所示。

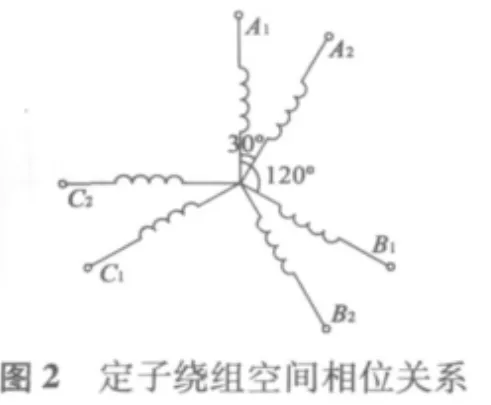

表1 两套定子绕组触发导通关系表
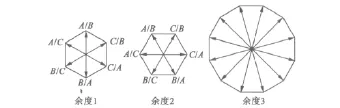
图3 两个余度分别独立工作时与合成工作时磁链示意图
2 余度电机数学模型
2.1 单通道无刷直流电动机数学模型
无刷直流电动机的三相定子电压平衡方程式如下:
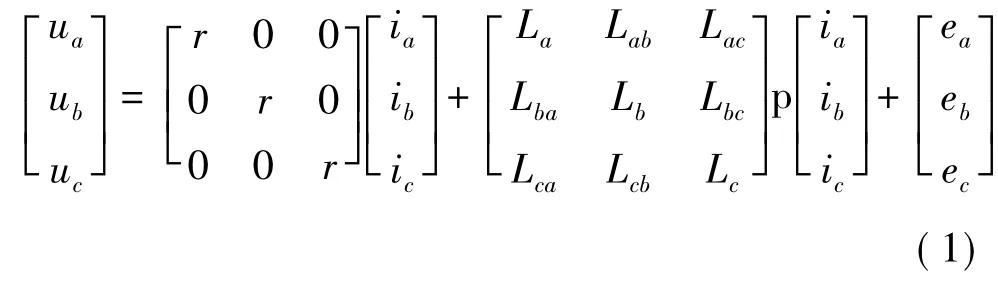
式中:ia、ib、ic为定子绕组相电流;ua、ub、uc为定子绕组的相电压;ea、eb、ec为定子绕组的反电动势;ra、rb、rc为每相绕组电阻;La、Lb、Lc为每相绕组自感;Lab、Lbc、Lca、Lba、Lcb、Lac为每两相绕组间互感;p 为微分算子。
由于定子三相绕组对称,则有:ra=rb=rc=r,La=Lb=Lc=L,Lab=Lba=Lbc=Lcb=Lac=Lca=M。式中L为无刷直流电动机定子绕组自感,M为无刷直流电动机定子绕组间互感。则式(1)可改为:
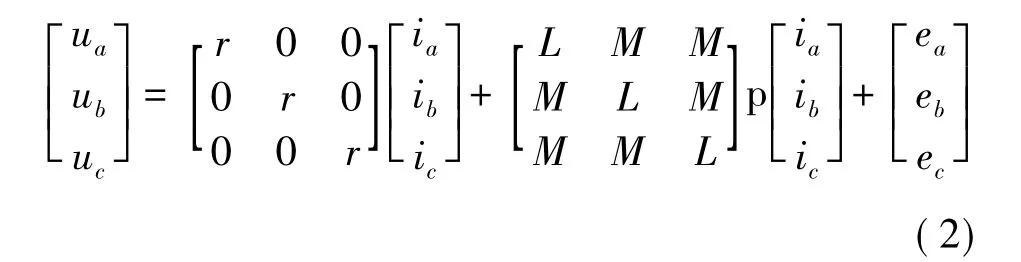
由于三相绕组为星形连接,且没有中线,则有:

式(2)、式(3)联立得:
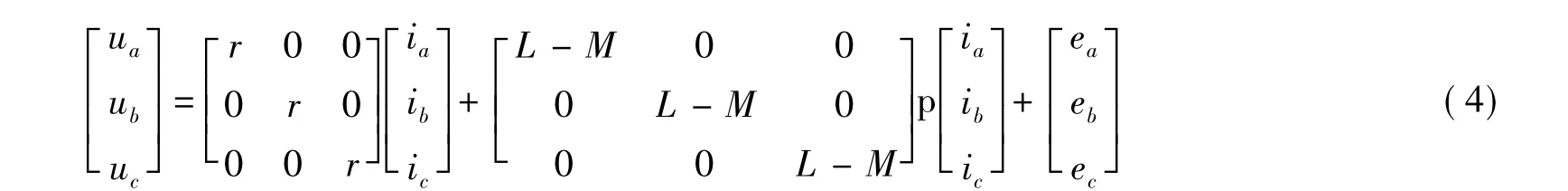
这时电机电磁转矩表达式可以转化:

式中:N为电枢绕组每相串联导体数;l为转子等效长度;R为电机转子半径;ω为转子转速。
电机的机械运动方程:
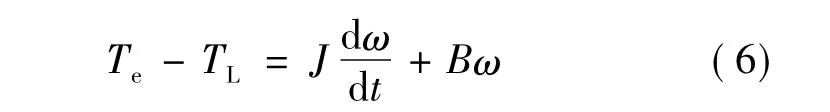
式中:T为负载转矩(N·m);J为转子惯性矩(kg·m2);ω为机械角速度(rad/s);B为粘滞系数。
2.2 双余度无刷直流电动机数学模型
电机模型是两套绕组在电气上彼此独立,共用一个转子,在此基础上,建立了数学模型。

式中:下标1为第1余度的电压、电流、电势变量。下标2为第2余度的电压、电流、电势变量。参数Ia为相绕组电感,m30、m120、m150和 m270分别为两相绕组差 30°、120°、150°与 270°电角度的互感。由于无刷直流电动机两个余度是三相绕组Y形连接,则有:
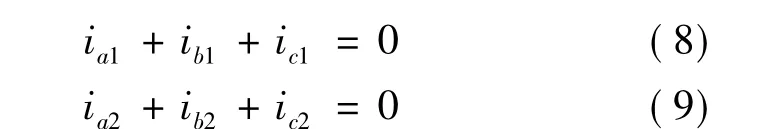

式中:La=la-m120。
于是式可简化:
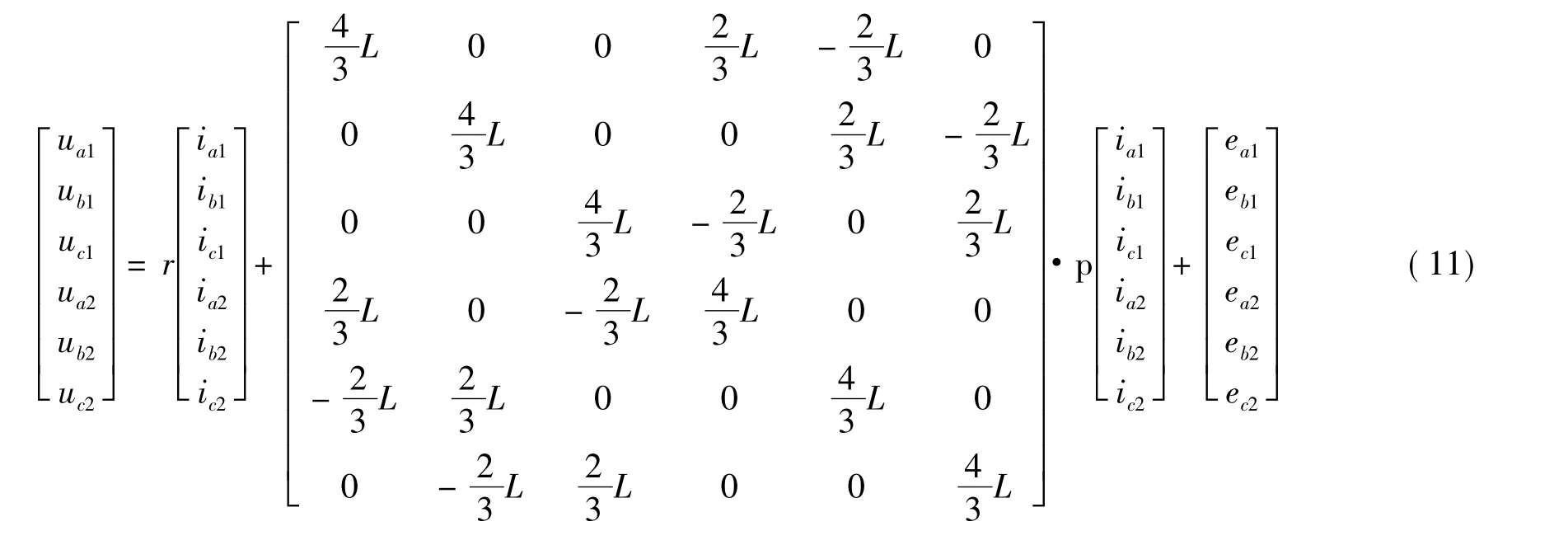
由此可得出双余度同时工作时的电磁转矩:
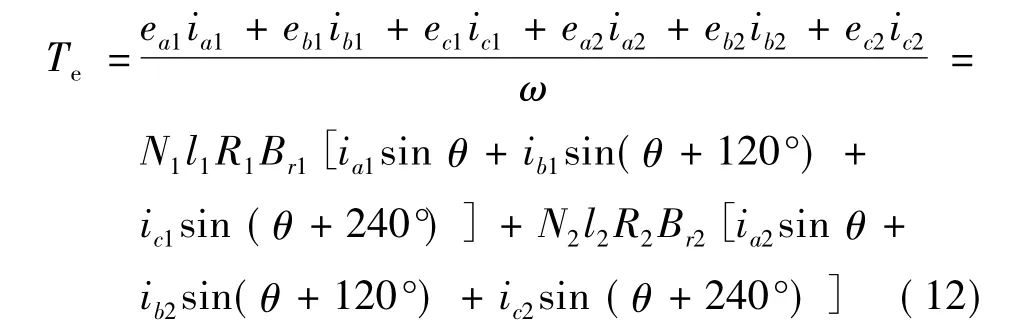
机械运动方程为:

式中:Te为电磁转矩;Tl为负载转矩;J为转子转动惯量;B为粘滞摩擦系数;ω为电动机的机械角速。这种模型是余度电机的相变量数学模型,由模型可得绕组故障后电动机的运行情况。
3 余度电动机的性能仿真、样机测试
3.1 电动机的仿真模型
本文利用数学模型,在MATLAB/Simulink环境中,对无刷余度电动机进行性能仿真,模型框图如图4所示。
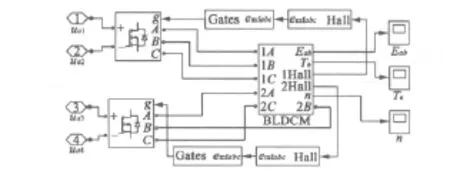
图4 基于Matlab/Simulink的电机性能仿真模型
3.2 电动机的仿真曲线、波形
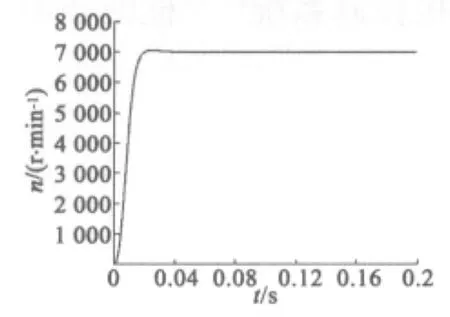
图5 电动机转速曲线

图6 电动机线反电势波形

图7 电动机力矩曲线
3.3 样机设计计算结果
磁路负荷:定子外径为57 mm,转子外径为33 mm,极对数为2,定子内径为35 mm,转子内径为13 mm,有效长度为72 mm,平均气隙磁密为0.636 2 T,定子齿磁密为1.565 8 T,定子轭磁密为1.128 8 T,转子轭磁密为0.899 T。
电性能:额定电压UN=27 V,额定转速nN=6 000 r/min,额定转矩 TN=0.5 N·m,额定输出功率PN≈300 W,空载转速no=8 000 r/min。
3.4 样机实测波形
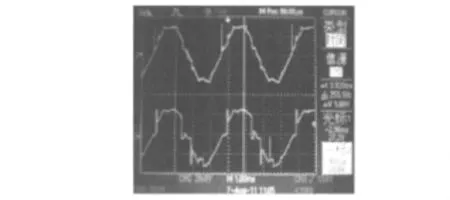
图8 电动机双余度线电压波形
图9 PWM调节下电动机线电压波形
3.5 样机实测数据
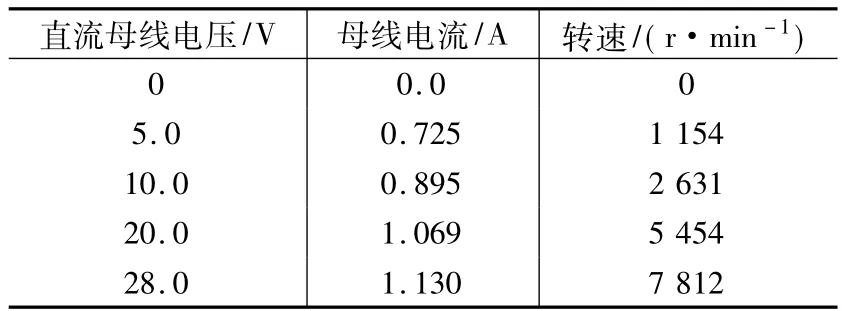
表2 电机的A余度开环空载调速实验
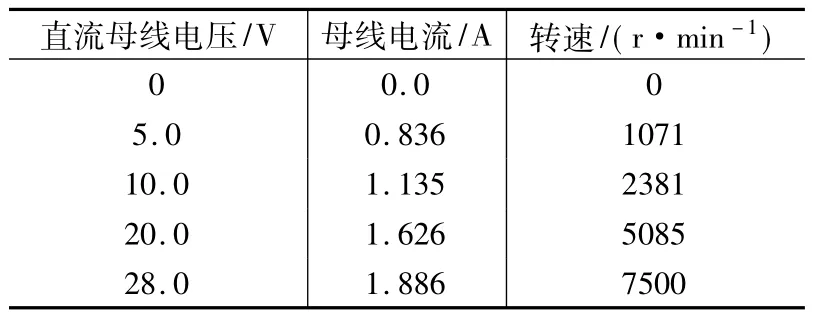
表3 电机的B余度开环空载调速实验
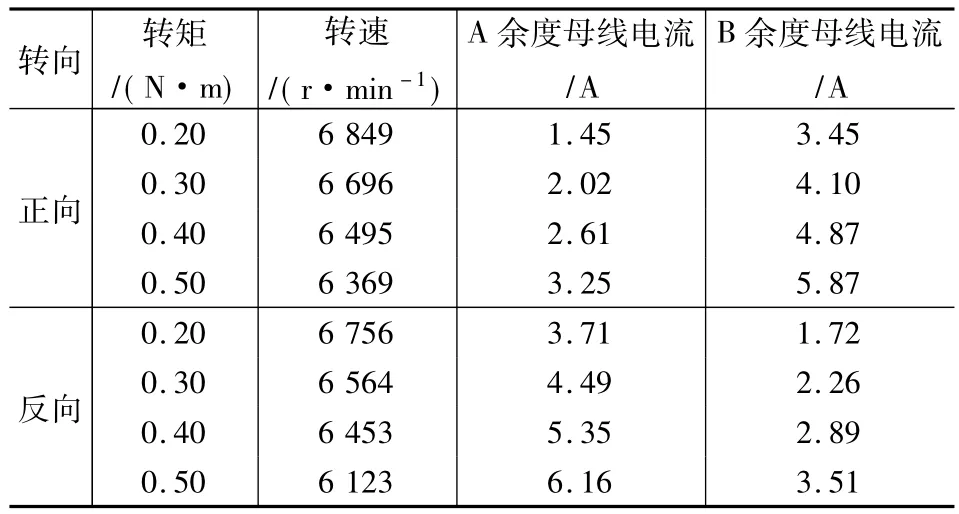
表4 电机的双余度开环负载调速实验
4 结 论
(1)双余度无刷直流电动机可单余度运行,另一余度备用;也可双余度额定运行,单余度故障运行。本文为提高效率,减小电机体积重量采用后者方案。
(2)由样机实测波形、数据可以看出,双余度电动机A、B组传感器位置均需在最佳状态,即两余度线电压均接近理想方波,这时空载电流为最小。样机A余度波形接近理想方波,在表2中电压28 V、转速为7 812 r/min对应较小的空载电流为1.13 A;而B余度波形畸变很大,在表3中电压28 V、转速为7 500 r/min对应较大的空载电流为1.886 A。
(3)由表4看出,双余度开环负载调速实验中,正转时转矩为 0.50 N·m、转速6 369 r/min,A余度母线电流为3.25 A、B余度母线电流为5.87 A;反转时转矩为 0.50 N·m、转速 6 123 r/min,而A余度母线电流为6.16 A、B余度母线电流为3.51 A。这足以验证正反转频繁切换的直流无刷电动机,其位置传感器的调整要考虑正反转的对称运行,不可追求单方向优越而忽略另一转向。
(4)波形和数据分析表明,本文重在强调传感器位置直接影响电机性能优劣,引起无刷直流电动机两余度运行性能不对称的主要因素是传感器工艺位置偏差导致某一余度性能变坏,要保证两余度性能对称,必须分别精调各自所对应的传感器位置。调试中的重要标志是电动机的空载电流最小或电压波形接近理想方波。本样机最后结果基本对称。
[1] 叶振锋,雷淮刚.基于MATLAB的无刷直流电动机控制系统仿真[J].微特电机,2006,34(3):19 -21.
[2] 薛永康.无刷直流电动机[J].微电机,1992(1):21.
[3] 叶宏,曾广商.三余度数字伺服控制系统结构设计与可靠性分析[J].固体火箭技术,2002,25(3):69 -72.
[4] 叶金虎.无刷直流电动机的设计(Ⅸ)[J].微特电机,2005,33(9):42.
[5] 毛鼎品.电子换向式无刷直流电动机的特性和应用[J].微电机,1985(2):23-27.
[6] 李文毓.无刷直流电动机[J].微电机,1986(4):17.
[7] 毛鼎品.高性能无刷直流电动机[J].微电机,1987(1):34.
[8] 马瑞卿,刘卫国,解恩.双余度永磁无刷直流电机速度伺服控制系统[J].电气传动,2006,36(1):41 -44.
[9] 文延,谢利理.CPLD在DSP无刷直流电机控制中的应用[J].微处理机,2004(3):58 -60.
[10] 俞斌.基于DSP的永磁无刷直流电动机伺服控制系统设计[J].电机与控制应用,2007,34(6):26 -28.
[11] 王勇.永磁无刷直流电机的应用和发展[J].科技资讯,2008,28:127-128.
[12] 雷跃荣.永磁无刷直流电机控制与无刷直流电机控制的比对[J].中国西部科技,2006(24):74-75.
