弧面分度凸轮的坐标测量原理及其实现
2011-07-19王晓飞
王晓飞 ,唐 琳
(1. 天津大学精密测试技术及仪器国家重点实验室,天津 300072;2. 江苏省计量科学研究院,南京 210007;3. 北京工业大学机电学院,北京 100124;4. 广州山锋测控技术有限公司,广州 510656)
弧面分度凸轮机构是一种两垂直轴间的间歇分度步进传动机构,具有高速、高精度、承载能力大、可靠性好、刚度高和强度大的优点,广泛应用于各种加工行业[1].弧面分度凸轮的廓面是一组围绕凸轮轴线旋转的凹槽曲线,可认为是从动件以某种运动规律运动留下的运动轨迹,其廓面加工准确与否直接影响凸轮机构的运动精度与传动质量,为保证弧面分度凸轮的加工精度,对凸轮廓面的检测是非常重要的;但是由于弧面分度凸轮廓面为复杂的空间不可展开螺旋面,加工难,成本高,无法用传统的常规仪器精确检测,在企业中弧面分度凸轮的检测手段也一直是个难题;我国在弧面分度凸轮廓面的静态检测方面的研究尚少,始终没有相关的检测产品出现,因此,研究弧面分度凸轮的几何静态检测方法具有重要的意义.
复杂空间曲面测量的常用工具是三坐标测量机(coordinate measuring machine,CMM)[2],因此笔者以CMM为测量工具,研究弧面分度凸轮的三坐标测评方法,并研发了一套基于 CMM的测量软件,实现对弧面分度凸轮的精密测量与评定,软件可应用于基于DMIS标准的三坐标测量机,具有通用性,可以通过精密测量控制凸轮廓面的加工质量,解决企业的实际问题,具有重要的使用价值.
1 凸轮廓面的数学模型
在弧面分度凸轮机构中,弧面分度凸轮是主动件,分度盘是从动件和输出构件,凸轮推动分度盘步进运动.当不考虑凸轮机构的安装误差和滚子几何形状误差等因素,仅考虑弧面凸轮廓面加工误差,通过从动件分度盘的运动规律反求主动件凸轮的轮廓曲线.运用微分几何的曲面理论及包络理论的有关知识,由分度盘滚子比较简单的曲面出发,应用共轭曲面原理、微分几何学和坐标变换原理获得弧面分度凸轮的理论轮廓曲面方程[3].
1.1 滚子建模
如图1所示,设滚子表面任何点的坐标为(xf,yf,zf),则
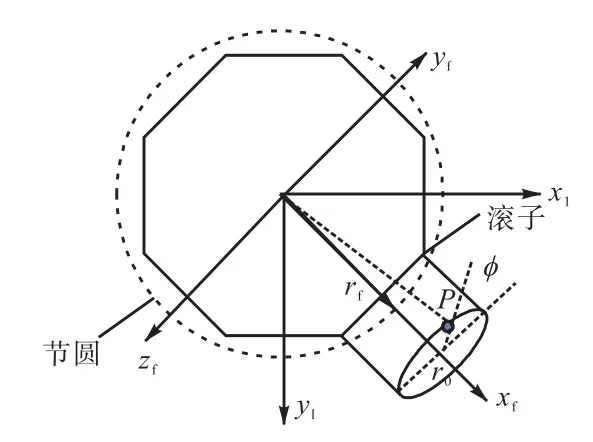
图1 滚子建模Fig.1 Model of roller

式中:δ为点到分度盘节圆的距离;rf、r0分别为分度盘与滚子半径;φ为测点与xfyf面的夹角.
1.2 坐标系变换
图 2中:Ofxfyfzf为分度盘动坐标系;O1x1y1z1为分度盘定坐标系;Oxyz为凸轮定坐标系;O2x2y2z2为凸轮定坐标系;Ocxcyczc为凸轮动坐标系.综合 4个坐标变换矩阵,推导出分度盘动坐标系 Ofxfyfzf变换到凸轮动坐标系Ocxcyczc的变换矩阵.θ和τ分别为凸轮与滚子的瞬时转角.
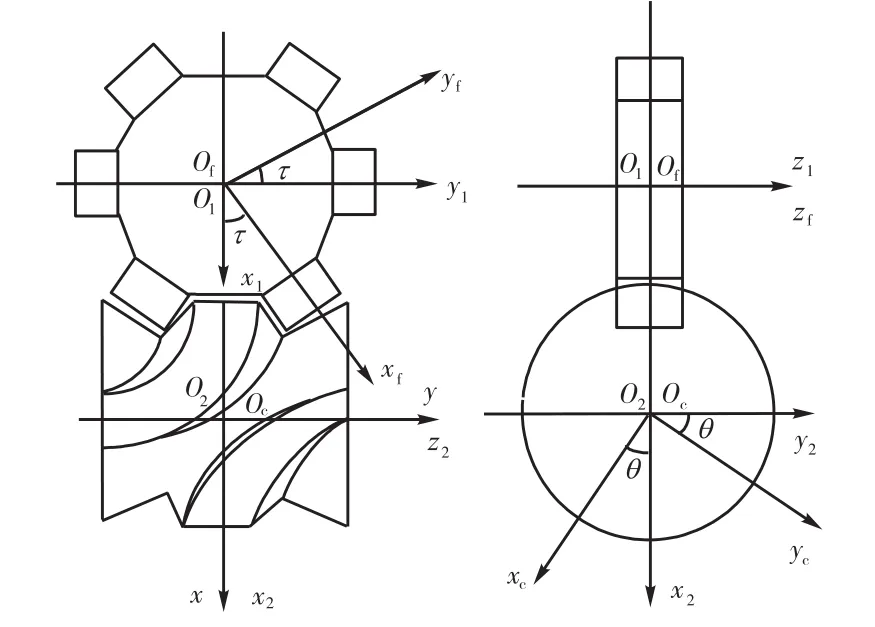
图2 坐标系变换Fig.2 Transfer of coordinate system
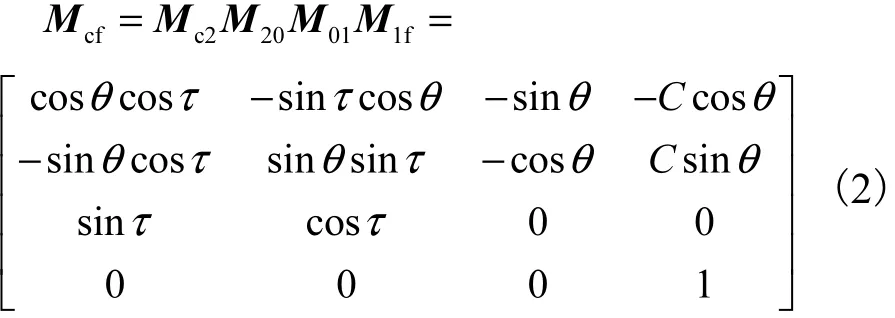
1.3 计算廓面坐标
弧面分度凸轮的理论轮廓曲面方程[4]可以表示为
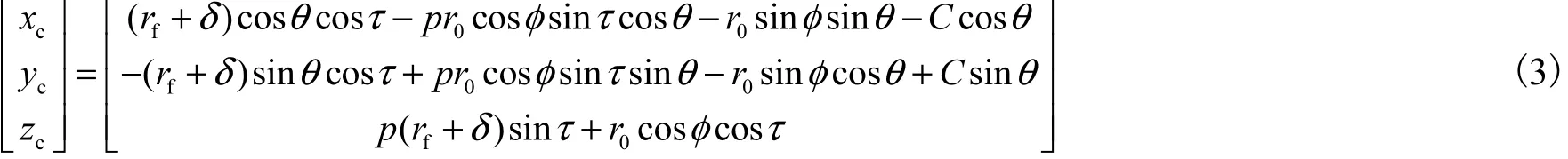
式中:p值取决于弧面分度凸轮的旋向,如果为左旋,p=1,若为右旋,p=-1;C 为凸轮与转盘的中心距.φ 和 τ的关系可由弧面分度凸轮的啮合方程[5]到,即
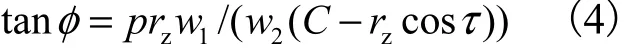
式中:w1、与 w2分别为凸轮与转盘角速度;rz为点到转盘中心的距离.
CMM 测量弧面分度凸轮,已知其几何参数与运动参数,给定采样参数φ和δ,通过式(1)和式(2),可求出凸轮廓面的理论坐标值.
2 建立坐标系
在三坐标上测量弧面分度凸轮,首先要建立凸轮坐标系[6],坐标系要求以凸轮轴线为 z轴,以轴线与凸轮上表面交点为原点,以原点与孔的连线为x轴方向,建立测量坐标系 Omxmymzm.评定误差时,测量数据与理论数据做比较,必须将测量坐标系转换为理论坐标系.如图3所示,凸轮理论坐标系为Ocxcyczc,Ocxcyczc与上表面距离为d,xm与x轴的夹角为α.为使测量坐标系与理论坐标系重合,将测量坐标系 Omxmymzm旋转一个角度 α[7],转换成坐标系 Oxyz,再将Oxyz向下移动距离 d,得到理论坐标系 Ocxcyczc,设测量坐标点[xM,yM,zM],通过转换坐标系 Mcm,得到转换后的坐标[xm,ym,zm].
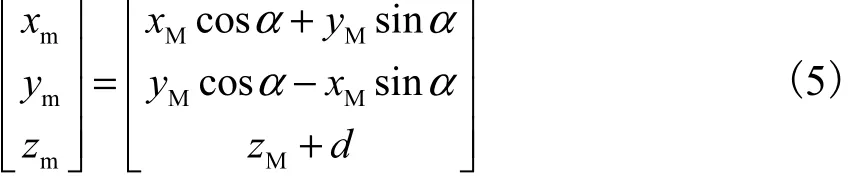
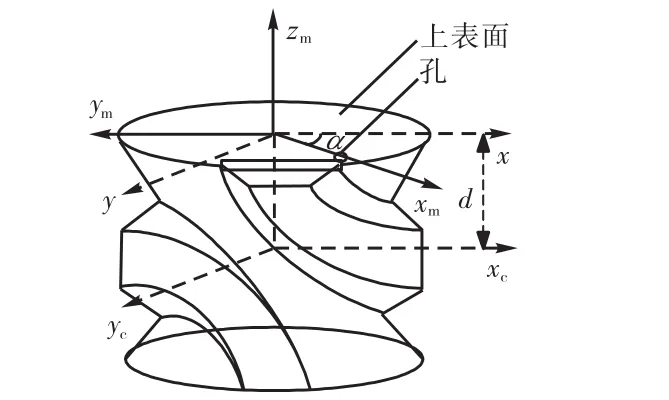
图3 建立凸轮坐标系Fig.3 Coordinate system of globoidal indexing cam
3 采样策略
在三坐标采样中,需要选择合适的测头角度,给定测量法向方向,设置移动点与采样点,规划测量路径.
3.1 选择测头角度
弧面分度凸轮各个凸轮廓面分布比较复杂,要保证能够测量所有点且不发生碰撞[8],测头角度的选择十分重要.如图 4所示,被测廓面与相邻廓面在纵向空间相交叠,在邻面的外边界上取一点,与相对应采样点内外边界相连,连线与 z方向的夹角分别为 θ0和 θ1,θ1>θ0,可见当测头与 z 方向夹角为 θ1时,可以满足测量该行测点而不发生碰撞.被测廓面的内边界与相邻廓面的外边界最大夹角时,可满足所有点的测量.
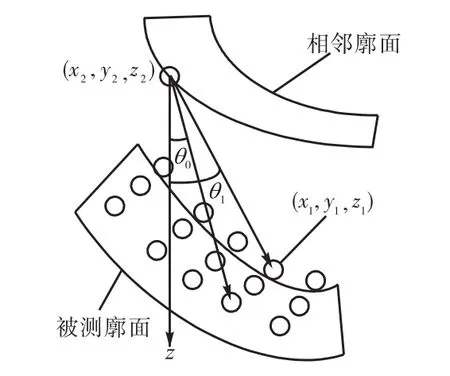
图4 测头角度Fig.4 Probe angle
设相邻廓面的外边界某点坐标为(x2,y2,z2),被测廓面的内边界某点坐标为(x1,y1,z1),两点在 z方向上的矢量为 k,夹角为 θi.则以所有角最大值作为测头方向θ的表达式为

3.2 计算移动点
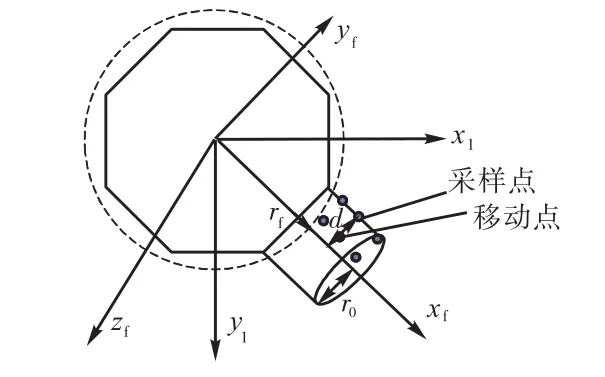
图5 移动点Fig.5 Moving points
如图 5所示,凸轮廓面上的采样点,同时也是滚子面上的点,沿着凸轮采样点的法向方向偏移一个距离d的点,取得移动点,在坐标系xfyfzf下移动点坐标为(xd,yd,zd).通过转换矩阵 Mcf,将移动点坐标系转换至测量坐标系,在测量坐标系下移动点坐标为(xD,yD,zD),则

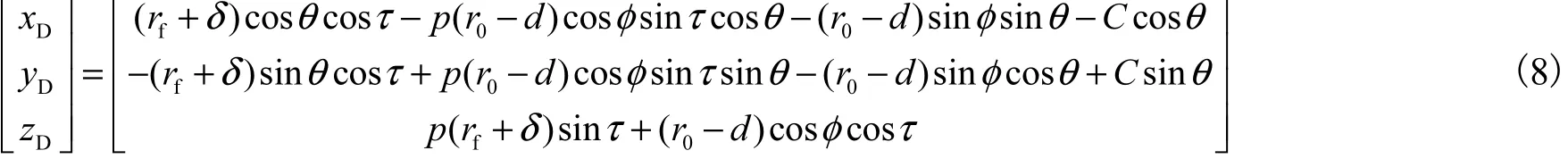
3.3 计算测点法向方向
设某采样点坐标为(xf,yf,zf),则该点的移动点坐标为(xD,yD,zD),两点间距离为 d,该点法向方向为(i,j,k),即

3.4 规划测量路径
采样路径如图6所示,当测头转换到最佳测量角度后,测头移动到某个移动点,然后沿着该点的法向方向上去取对应的采样点,测完该采样点再回到原移动点,采完一行后,移动到下一行的临近点,然后循环运行,直到采完所有的点.
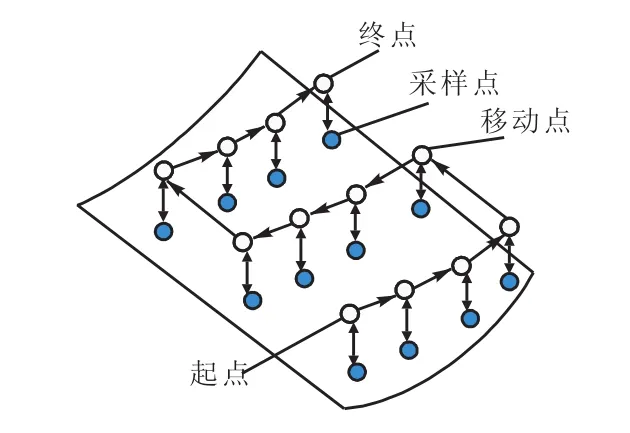
图6 采样路径Fig.6 Sampling route
4 误差评定
由于我国目前还没有弧面分度凸轮的国家标准,因此没有统一的弧面分度凸轮的误差项目的定义.弧面分度凸轮的曲面为复杂曲面,其精度影响整个机构的运动精度.从几何精度而言,根据复杂曲面测量的特征线原理,控制复杂曲面的精度可以通过控制特征线的精度来实现.因此可以选取螺旋面的螺旋线和轴向截面的廓线定义弧面分度凸轮的误差测量项目:廓面偏差、螺旋线偏差和轴向截面廓线偏差;通过对这几个测量项目的评定,来反映弧面分度凸轮廓面的加工质量.
4.1 廓面偏差
廓面偏差:包容实际廓面且距离最小的的2个平行廓面间的法向距离.
弧面分度凸轮的廓面偏差采用构造曲面法,将理论点数据拟合为曲面,求实际点到曲面的距离.该方法的优点是无须坐标系严格重合[9],既可以提高测量数据的精度,又克服了坐标测量机空间定位精度的影响.由弧面分度凸轮的数学模型求出轮廓面上的一系列数值点,通过这些理论点构造理论曲面.将理论点坐标代入双4次EB样条曲面方程,可以构造出插值廓面,即

式中:E为 EB样条参数方程;V为理论点坐标方程;U和W为构造变量方程,0<u<1,0<w<1.
设某测量点坐标为(xj,yj,zj),理论廓面坐标为(Px,Py,Pz),以该点到理论轮廓面上的距离为该点偏差[4],即
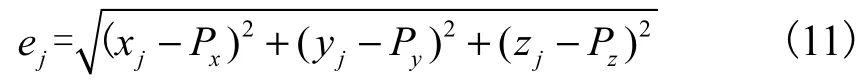
取轮廓面上所有采样点正向偏差与负向偏差的最大值之和为廓面偏差,即

4.2 螺旋线偏差
螺旋线偏差:在凸轮动程范围内,包容实际螺旋线且距离最小的的2条理论螺旋线间的法向距离.
根据螺旋线的定义,满足0δ=的廓面坐标点构成螺旋线.通过计算理论特征线上的离散点,然后沿着法向测量实际点的坐标,计算理论点与实际点的距离,若实际点位于法向外侧距离为正,实际点位于法向内侧距离为负,以法向两侧点距离的最大值为螺旋线偏差.螺旋线偏差评定采用点对点方法[10],理论点坐标为(xj,yj,zj),实测点坐标为(x′j,y′j,z′j),该点偏差为[4]
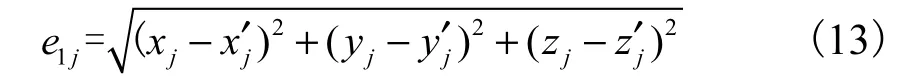
取所有采样点正向偏差与负向偏差的最大值之和为螺旋线偏差,即

4.3 轴向截面廓线偏差
轴向截面廓线偏差:凸轮动程范围内,廓面与过轴线的平面相截,包容实际廓线且距离最小的2条理论廓线间的法向距离.
根据轴截面廓线的定义,设轴截面与参考面成 α角,满足 y/x=tan,α条件的廓面坐标点构成轴截面廓线.轴向截面廓线误差评定采用点对点方法[11],设 zj为廓线点纵坐标,z′j为廓线实测点纵坐标,该点偏差为[4]

取所有采样点正向偏差与负偏差的最大值之和为轴向截面廓线偏差,即

5 应用实例
选用海克斯康公司Global Performance系列型号为7107型的三坐标测量机,并选用测球半径为1 mm的红宝石测球和TP2型触发式测头,运行弧面分度凸轮测量软件,以测量弧面分度凸轮廓面偏差为例.凸轮参数见表1,廓面测量点实测值及偏差值见表2.

表1 弧面分度凸轮参数Tab.1 Parameters of roller-gear cam
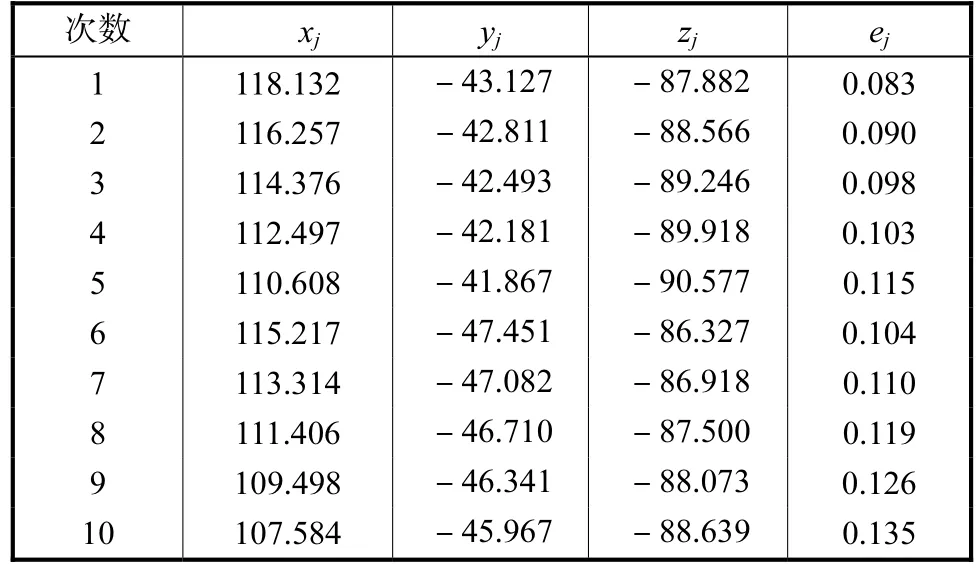
表2 廓面测量点实测值及偏差值Tab.2 Results of measured points and errors mm
再根据式(12)取轮廓面上所有采样点正向偏差与负向偏差的最大值之和为廓面偏差,即
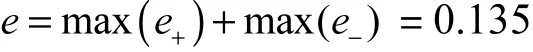
6 结 语
对弧面分度凸轮复杂廓面三坐标测量技术中的理论基础、数据获取、测量路径规划以及误差评定等关键技术进行了研究,在研究基础上开发了测量软件,可以测量并评定弧面分度凸轮的廓面偏差、螺旋线偏差和轴向截面廓线偏差等,实验验证了测量方法的可行性,该方法和软件具有很好的实用和推广价值.
[1] 胡秉辰. 分度凸轮机构纵横谈[J]. 机械设计与研究,1994(2):37-39.Hu Bingcheng. Talking about indexing cams mechanism[J]. Machine Design and Research,1994(2):37-39(in Chinese).
[2] 石照耀,谢华锟,费业泰. 复杂曲面测量模式与关键技术[J]. 工具技术,2000,34(1):31-34.Shi Zhaoyao,Xie Huakun,Fei Yetai. Models and key technologies of complex surface measurements[J]. Tool Engineering,2000,34(1):31-34(in Chinese).
[3] 刘昌祺,牧野洋,曹西京. 凸轮机构设计[M]. 机械工业出版社,2005.Liu Changqi,Mu Yeyang,Cao Xijing. Cam Mechanism Design[M]. Beijing:China Machine Press,2005(in Chinese).
[4] 唐 琳,王晓飞,林家春. 基于 CMM 的弧面分度凸轮精密测量软件的开发[J]. 机械传动,2011,35(5):59-62.Tang Lin,Wang Xiaofei,Lin Jiachun. Development of software of precise measuring roller gear cam based on CMM[J]. Journal of Mechanical Transmission,2011,35(5):59-62(in Chinese).
[5] 王其超,肖正扬,马丽敏,等. 弧面分度凸轮机构啮合特性的研究[J]. 农业机械学报,1994,25(增):1-7.Wang Qichao,Xiao Zhengyang,Ma Limin,et al. The research of globoidal indexing cam mechanism meshing characteristic[J]. Transactions of the Chinese Society for Agricultural Machinery,1994,25(Suppl):1-7(in Chinese).
[6] Ge Rongyu,Feng Xianying,Song Xianchun,et al.Measurement with CMM and transmission quality evaluation of globoidal cam profile surface[J]. China Mechanical Engineering,2008,19(3):285-288.
[7] Chang Wen-Tung,Wu Longlong,Fuh Kuang-hua,et al. Inspecting profile errors of conjugate disk cams with coordinate measurement[J]. Journal of Manufacturing Science and Engineering,2008,130(1):011009.
[8] 白作霖,赵汝嘉,张定红,等. 基于 CNC坐标测量机的自由曲面曲线自动检测及处理系统[J]. 西安交通大学学报,1995,29(10):75-80.Bai Zuolin,Zhao Rujia,Zhang Dinghong,et al. Autoinspection and process system of free curves and sculptured surfaces for coordinate measuring machines[J].Journal of Xi’an Jiaotong University,1995,29(10):75-80(in Chinese).
[9] Lin Jiachun,Tang Lin,Shi Zhaoyao. Inspection of spatial cams using coordinate measuring machine[C]//10th International Symposium on Measurement and Quality Control. Japan:2010:E41-44.
[10] 姚 平,刘雄伟,袁哲俊,等. 自由曲面设计的新方法:四次 EB样条方法[J]. 组合机床与自动化加工技术,1990(7):9-14.Yao Ping,Liu Xiongwei,Yuan Zhejun,et al. The new method of free surfaces design:Quartic EB-spline method[J]. Modular Machine Tool and Automatic Manufactoring Technique,1990(7):9-14(in Chinese).
[11] 王海燕,赵汝嘉,刘昌祺. 弧面分度凸轮轮廓误差评定的数学模型[J]. 西安交通大学学报,1999,33(11):96-99.Wang Haiyan,Zhao Rujia,Liu Changqi. Error evaluation of globoidal indexing cam profile[J]. Journal of Xi’an Jiaotong University,1999,33(11):96-99(in Chinese).
