可倾瓦轴承瓦块摆动特性
2011-07-18王永亮刘占生钱大帅
王永亮,刘占生,钱大帅
(哈尔滨工业大学能源科学与工程学院,150001哈尔滨,vibw@qq.com)
可倾瓦轴承瓦块摆动特性
王永亮,刘占生,钱大帅
(哈尔滨工业大学能源科学与工程学院,150001哈尔滨,vibw@qq.com)
研究可倾瓦轴承瓦块摆动几何关系,基于分离变量法建立了有限长轴承油膜压力模型及瓦块力矩平衡方程,获得瓦块摆角与轴承参数之间的函数关系;以瓦块包角为80°、支点偏移量为0.5的四瓦块可倾瓦轴承为研究对象,计算分析其瓦块的摆动特性.理论推导表明,瓦块静平衡摆角只与瓦块结构参数、轴颈相对瓦块偏心率、间隙比有关,而与轴颈转速、油膜粘度等无关;数值仿真结果表明,当瓦块结构参数一定时,瓦块静平衡摆角随原始偏心率增大呈先增大后减小趋势,随轴承间隙比增大呈线性增加趋势.研究结果为建立工程实用的可倾瓦轴承非线性油膜力模型提供理论依据.
可倾瓦;瓦块摆动;原始偏心率;间隙比
随着转子-轴承系统的大型化、高速化发展,支承转子的径向可倾瓦轴承稳定性问题越来越突出[1],在实际工程中,可倾瓦轴承支承的转子系统的油膜失稳现象偶有发生[2-3].可倾瓦滑动轴承油膜力模型是可倾瓦轴承-转子系统非线性动力学特性分析的基础和关键,因此有必要建立可靠的可倾瓦轴承非线性油膜力模型.目前,可倾瓦轴承非线性油膜力求解方法主要有直接求解法[4-5]、数据库法[6-7]、非线性油膜力公式 3 类.直接求解法计算精度高,但计算效率较低.数据库法效率高,但建库过程复杂,通用性不强.Okabe E P[8]利用短圆柱瓦轴承模型进一步推导了可倾瓦滑动轴承非线性油膜力模型,对比分析了该模型与有限差分求解雷诺方程计算结果,但未给出瓦块摆角公式.王丽萍等[9-10]基于瓦块和轴颈间的运动耦合关系,建立瓦块局部坐标系统;通过坐标变换,将瓦块和轴颈运动相关的全局广义位移矢量转换为局部动坐标系下轴颈的位移矢量;利用求解固定瓦轴承动力特性的方法求得的局部动坐标系下的油膜力;进而将局部坐标系下油膜力精确转换为全局广义坐标系下的表达形式.但是瓦块摆角需要迭代求解.
分析计算可倾瓦滑动轴承油膜动力特性时,给定轴颈在可倾瓦轴承中的扰动位移和扰动速度,如果能够快速获得瓦块摆角,从而快速获得油膜厚度分布规律,高效求解可倾瓦轴承油膜动力特性,对于可倾瓦滑动轴承动力特性的研究,以及可倾瓦轴承支承转子系统非线性动力学特性分析来说是具有重要意义的.
本文推导可倾瓦轴承瓦块油膜特性几何关系,并基于分离变量法建立有限长可倾瓦块油膜压力近似解析表达式,根据静平衡时瓦块受油膜压力力矩平衡,推导可倾瓦块摆角与可倾瓦轴承几何参数、间隙比、及原始偏心率间关系式,最后研究摆角随间隙比和原始偏心率变化规律.
1 可倾瓦瓦块几何关系

图1 可倾瓦摆动几何关系示意图
图1(a)为一静止不动的轴颈和其支撑可倾瓦瓦块,轴颈半径为R,可倾瓦块与轴颈之间半径间隙为 C,瓦块轴向长度为 L,图中 Φ1、Φ2、Φ3为瓦块原始几何角,确定了瓦块的结构参数.可倾瓦块与轴颈之间充满了粘度为μ的润滑介质.由于轴颈是没有运动的,瓦块圆弧中心O、轴颈中心Oj以及瓦块支点Op处于同一直线上,轴颈中心和瓦块中心间距离定义为原始偏心距e.
轴颈以角速度Ω旋转,假定轴颈旋转过程中,轴颈中心Oj不动,根据流体润滑理论知,可倾瓦块必定绕支点转动一定角度φ,如图1(b)所示.这时,可倾瓦轴承瓦块油膜特性就转化为轴承中心O'、轴颈中心为Oj、偏心距为E、偏位角为α的有限弧度圆瓦轴承油膜特性,进而利用圆瓦轴承油膜相关理论分析可倾瓦块特性.图1(b)中θ为油膜周向坐标,起始位置为名义最大油膜厚度处.θ1、θ2、θ3定义为油膜特征角,分别为瓦块出油边边界,瓦块支点角,瓦块进油边边界.
由图1(b)可知,轴颈开始旋转后,油膜特征角与瓦块原始几何角有如下关系:

图1(c)为图1(b)相关几何关系放大图,根据三角关系可得

将式(2)带入式(3)整理后可得

定义ε0=e/C为原始偏心率,ψ=C/R为半径间隙比.对式(4)进行无量纲化,得
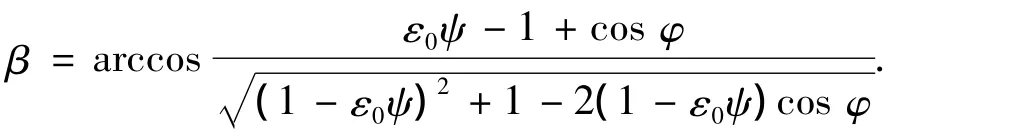
又由图1(c)可得知瓦块摆动后实际偏位角表达式为

2 可倾瓦瓦块润滑油膜特性分析
本文研究瓦块摆动达到平衡后的摆角,即轴颈在轴承中无涡动,油膜只有动压效应,没有挤压效应.因此忽略流体润滑雷诺方程中所有动态效应项,在此条件下适合图1(b)中油膜润滑Reynolds方程形式如下:

式中:p为瓦块与轴颈之间油膜的压力;z为油膜轴向坐标,其零点在瓦块中分面处;h为油膜厚度,h=C(1+ εcos θ).轴向和周向边界条件为

利用分离变量法对雷诺方程进行求解,以获得压力近似解析解.
假设方程(7)解的形式如下:

其中,M和N分别为变量θ和z的二次可微函数,将式(8)带入式(7)整理后可得

式中:

由分离变量法特性可知,式(12)右端项必然为 0,即

对式(13)积分两次并带入边界条件即可获得周向油膜分布:

式中:
C1=-I1/I2;C2=-(I1(θ1)-I2(θ1)·I1/I2);Ii=Ii(θ3)-Ii(θ1),i= 1, 2,Ii(θ).具体表达式见附录.
因此,油膜压力分布表达式为

3 瓦块摆动规律
如图2所示,假设可倾瓦瓦块摆动到某一平衡位置,此时摆角为定值,根据以上可倾瓦瓦块润滑油膜特性分析,即可获得该状态时油膜压力分布.

图2 微元对支点力矩示意图
取角度为θ的dθ微元,根据受力分析可知,该微元对瓦块支点的力矩为
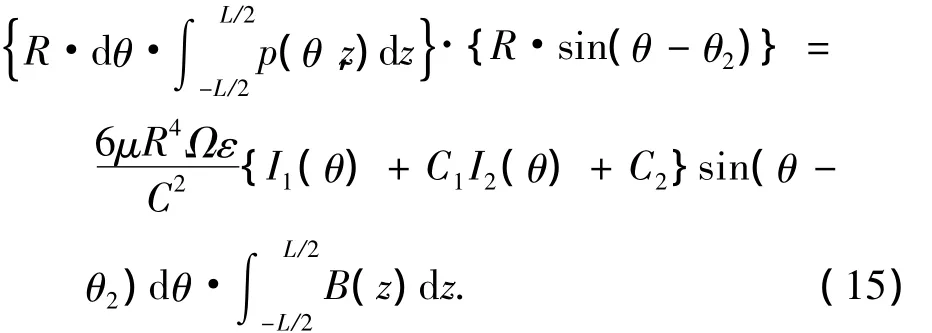
在瓦块油膜承载区内对式(15)积分,并根据当瓦块处于静平衡状态时,油膜力对支块的总力矩为零,对力矩方程进行化简即可获得如下总力矩表达式:

整理后即可得到如下可倾瓦块平衡方程:

可见,可倾瓦瓦块达到静平衡时,其摆角φ与瓦块参数、间隙比及原始偏心率有关,而与轴颈转速、油膜粘度等参数无关.
当可倾瓦轴承瓦块参数给定后,式(17)只与可倾瓦瓦块摆角φ、轴承间隙比ψ及原始偏心率ε0有关,即瓦块摆角方程可写成

由式(18)可知,当瓦块原始参数确定后,瓦块摆角φ与轴承间隙比ψ及原始偏心率ε0成隐函数关系,1个方程3个变量,可通过给定其中一变量来考察其他两变量间关系.
4 算例
为定性分析瓦块摆角与轴承间隙比及原始偏心率之间的关系,以哈尔滨汽轮机厂300 MW汽轮机高中压转子支承四可倾瓦轴承为例,分析给出瓦块摆角的影响规律.四可倾瓦单个瓦块包角为80°,入口边到支点的包角为40°,根据前面分析可知,对应瓦块几何参数为:Φ1=220°,Φ2=180°,Φ3=140°. 联合式(1)、(5)、(6)、(14)和(18),即可求获得此可倾瓦块摆角随可倾瓦轴承间隙比及原始偏心率变化规律.
图3为瓦块处于静平衡时,摆角随轴承间隙比变化规律,可以看出,可倾瓦轴承瓦块摆角随轴承间隙比的增大而呈线性规律增大,曲线斜率随原始偏心率增大而变化.当轴承间隙比为零时,瓦块和轴颈紧贴,瓦块无法摆动,此时摆角为零.

图3 瓦块摆角随轴承间隙比变化
图4为给定间隙比,瓦块处于静平衡时,可倾瓦瓦块摆角随原始偏心率变化规律.由图可知,瓦块摆角随原始偏心率的增大呈抛物线规律变化,先增大而后减小,当原始偏心率接近0或1时,瓦块摆角接近0.从图4还可看出,当可倾瓦轴承间隙比一定时,瓦块摆角随原始偏心率的增大而增大,与图3分析结论一致.
由图3及以上分析可知,瓦块摆角与间隙比呈线性关系,且间隙比为零时,瓦块摆角为零,当原始偏心率为0或1时,摆角亦为0.因此设瓦块摆角表达式为

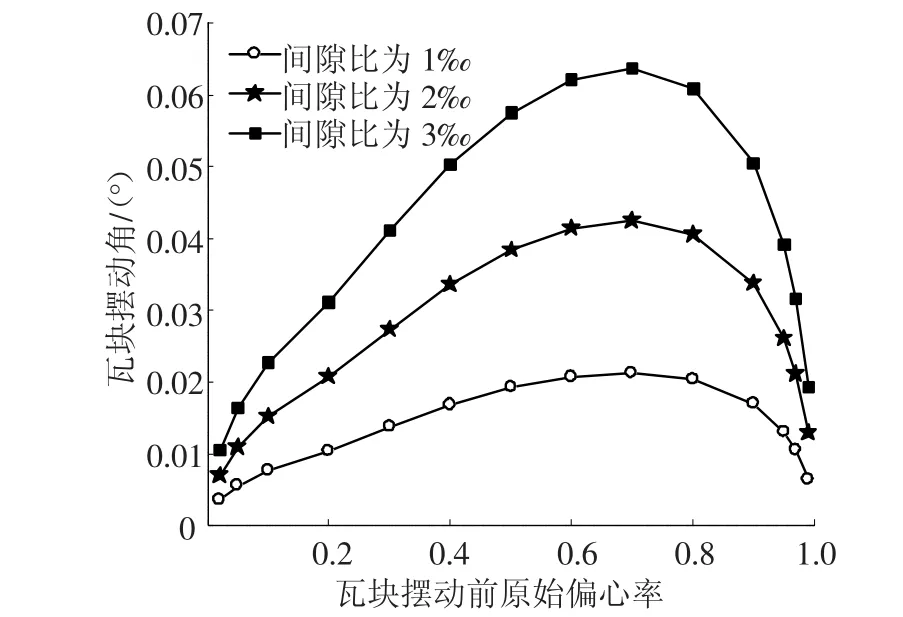
图4 瓦块摆角随原始偏心率变化
通过曲线拟合获得G(ε0)表达式,进而获得瓦块摆角函数关系:

图5为间隙比为2‰时,拟合曲线与迭代求解获得的瓦块摆角对比图,可以看出,式(19)能够表达摆角与间隙比和原始偏心率之间的关系.
可倾瓦块摆角直接影响到可倾瓦轴承的瓦块油膜厚度及油膜边界条件,进而影响油膜压力分布规律及可倾瓦轴承静、动特性.
由式(19)可知,已知轴承间隙比ψ及原始偏心率ε0后,即可获得摆角φ.为考察摆角对油膜厚度及油膜压力分布规律的影响,令间隙比ψ=2‰,原始偏心率依次为 0.4、0.5、0.7、0. 7,对应瓦块摆角为 0.033、0.038、0.042、0.043.

图5 迭代求解值与拟合曲线对比
图6为不同摆角对油膜厚度的影响,从图中可明显看出,当瓦块摆角从0.033增大到0.043时,油膜度逐渐减小,当摆角为0.033时,瓦块与轴颈形成收敛油楔,油膜区域为瓦块整个表面区域;当摆角增大到0.043时,最小油膜厚度位于距离瓦块尾端附件瓦块表面,正压油膜区域为瓦块首端至最小油膜厚度处.由此可见,瓦块摆角对油膜厚度及边界条件有很大影响.

图6 间隙比2‰不同瓦块摆角下油膜厚度
图7为不同摆角时油膜压力分布,从图可以看出,瓦块摆角直接影响了油膜压力分布,同时可以很明显看出,摆角影响了润滑油膜边界.

图7 间隙比2‰不同瓦块摆角时油膜压力分布规律
以上以哈汽300 MW汽轮机高中压支承四可倾瓦轴承为例,给出了可倾瓦块摆角随轴承间隙比及原始偏心率的定性变化规律.对于不同包角的可倾瓦,瓦块摆角数值上不同,但其摆角随间隙比和原始偏心率的定性变化规律是一致的.
5 结论
1)当轴颈在轴承中位置一定时,可倾瓦块摆角只与原始偏心和间隙比有关,而与转速、粘度等参数无关;
2)在同一可倾瓦轴承间隙比下,可倾瓦块摆角随原始偏心率增大先增大,而后减小,呈抛物线规律变化,当原始偏心率为0或者1时,瓦块摆角为零;
3)当可倾瓦轴承瓦块原始偏心率不变时,可倾瓦块摆角随轴承间隙比增加而呈线性规律增大.


[1]WHITE M F,SHAN S H.The subsynchronous dynamic behavior of tilting pad journal bearings[J].Journal of Tribology, 1992,114:167-173.
[2]虞烈,谢友柏.可倾瓦轴承油膜动力不稳定性的实验研究[J].实验力学, 1989,4(4):380-386.
[3]CAVALCA K L,DEDINI F G.Experimental analysis of tilting pad journal bearing influence in a vertical rotating system[C]//Fifth International Conference on Rotor Dynamics(IFToMM).Darmstadt,Germany:Technische Universitat Darmstadt,1998:571 -582.
[4]PAGANO S,ROCCA E,RUSSO M,et al.Dynamic behavior of tilting pad journal bearings[J].Inst Mech Engrs, 1995,209(J4):275 -285.
[5]ISSAN A M,MAURICE L A.Numerical study of some nonlinear dynamics of a rotor supported on a three-pad tilting pad journal bearing[J].Journal of Vibration and Acoustics, 2005,127:262 -272.
[6]王文,张直明.油叶型轴承非线性油膜力数据库[J].上海工业大学学报,1993(4):299-305.
[7]王德强,张直明.Jeffcott转子-滑动轴承系统不平衡响应非线性仿真[J].振动与冲击, 1999,18(1):57-62.
[8]OKABE E P,CAVALCA K L.Rotordynamic analysis of systems with a non-linear model of tilting pad bearings[C]//Seventh International Conference on Rotor Dynamics(IFToMM),Vienna,Austria:Technische Universitat Wien,2006:Paper-ID 222,10.
[9]王丽萍,乔广,郑铁生.可倾瓦轴承的完整动力分析模型及计算方法[J].机械工程学报, 2008,44(1):75-80.
[10] YAN ZhiYong,WANG Liping,QIAO Guang,et al.An analytical model for complete dynamical coefficients of a tilting-pad journal bearing[J].Tribology International, 2010,43:7-15.
Swing characteristic of pads in tilting pad bearing
WANG Yong-liang,LIU Zhan-sheng,QIAN Da-shuai
(School of Energy Science and Engineering,Harbin Institute of Technology,150001 Harbin,China,vibw@qq.com)
The geometric relations of pad on tilting-pad bearing were studied,the relationship between tile pendulum angle and structural parameters were established by the oil-film force model of finite length tilting pad bearing and equilibrium equation,and the basic law of tile pendulum angle change was analyzed.The study shows that the tile pendulum angle is determined by the pad structural parameters,the eccentricity ratio of tilting pad bearing and the clearance ratio,but independent of shaft rotating speed,viscosity of lubrication oil,etc.A case study of a tilting pad bearing with 80 deg pad arc angle,0.5 offset was performed to illustrate the law of tile pendulum angle varies with eccentricity ratio and clearance ratio.It is revealed that,when the structural parameters of tilting pad bearing are constant,the tile pendulum angle increases first and then decreases with the original eccentricity ratio increases,and increases linearly with the increasing of bearing clearance ratio.
tilting pad bearing;swing characteristic;eccentricity ratio;clearance ratio
TH133.3
A
0367-6234(2011)09-0062-05
2010-04-08.
国家自然科学基金资助项目(10632040).
王永亮(1983—),男,博士研究生;
刘占生(1962—),男,教授,博士生导师.
(编辑 杨 波)
