高超声速飞行器非线性H∞姿态控制设计

王 延，周凤岐，周 军，郭建国

（西北工业大学 精确制导与控制研究所，710072 西安，wangyan991926@sina.com）

由式(1)可得:

那么式(2)中的各个函数计算为

闭环非线性系统式(2)，式(9)渐近稳定.

2)当w≠0，得出

高超声速飞行器非线性H∞姿态控制设计

王 延，周凤岐，周 军，郭建国

（西北工业大学 精确制导与控制研究所，710072 西安，wangyan991926@sina.com）

针对高超声速飞行器倾斜转弯姿态跟踪控制问题，将非线性耦合系统的姿态跟踪控制表述为非线性H∞控制的指令误差状态空间实现形式.基于非线性系统γ－耗散性及L2增益设计准则，设计满足Hamilton-Jacobi-Isaacs不等式的光滑可微储能函数.在一定假设条件下，利用非线性系统在局部空间内线性伴随系统的Riccati微分方程，获得非线性H∞控制问题在邻近指令误差状态空间的局部空间解，来解决非线性耦合系统的H∞控制问题.实验结果表明，该方案避免了复杂的Hamilton-Jacobi-Isaacs不等式求解过程.

高超声速飞行器;非线性H∞控制;L2增益;Hamilton-Jacobi-Isaacs不等式

高超声速飞行器控制问题中稳定性、控制性能以及鲁棒性等是其主要关心的问题.目前对高超声速飞行器鲁棒控制研究大部分集中在纵向模态，且大部分都是以忽略模型之间相互耦合影响为前提的［1－3］，而非线性鲁棒控制方法普遍是基于动态逆或基于微分几何精确反馈线性化的控制策略［4－7］.

基于微分几何的精确反馈线性化过程中要进行大量繁琐的高阶微分运算，动态逆方法对建模误差非常敏感［8］，需要实现系统精确建模.倾斜转弯技术能够适应高超声速飞行器气动外形对空气动力学参数以及大气条件变化敏感、气动特性复杂等特性要求，其动力学系统快时变、强耦合.从已有文献可以看出高超声速飞行器纵向控制问题已经相当复杂，考虑非线性耦合模型时，控制问题将变得更复杂，这给实际应用带来较大的难度.

非线性H∞控制作为一种先进的鲁棒控制方法，其应用因为繁琐的 HJI(Hamilton-Jacobi-I-saacs)不等式求解而受限.文献［9－10］基于L2增益分析，提出了平滑仿射非线性系统H∞控制的完整解决方案.文献［11－12］将上述方法扩展到含有非光滑摩擦力的动力学模型，并应用于机械控制.本文针对高超声速飞行器非线性耦合系统倾斜转弯姿态跟踪控制问题，建立高超声速飞行器H∞倾斜转弯姿态跟踪模型，为了解决该非线性耦合系统控制问题，放宽文献［11－12］的应用条件，设计非线性H∞姿态跟踪控制器.该方案通过求解非线性H∞控制问题在邻近指令状态点的局部空间解，避免非线性H∞控制设计中复杂的HJI不等式求解过程，通过仿真验证了该方法满足高超声速飞行器倾斜转弯姿态跟踪控制设计要求，具备较好的鲁棒性能.

1 高超声速飞行器姿态跟踪动力学模型

高超声速飞行器倾斜转弯H∞姿态控制设计目的是设计H∞控制器使得飞行器滚转角γ跟踪滚转角指令γc，攻角α跟踪攻角指令αc，保持侧滑角β跟踪βc=0，且系统内部渐近稳定.因此选取状态变量为

建立高超声速飞行器倾斜转弯姿态跟踪动力学模型为

由式(1)可得:

那么式(2)中的各个函数计算为

式中c1～c6为常数参量.

跟踪动力学模型式(2)没有作γ、α、β小角度假设，没有作三通道解耦处理，是一个严重非线性耦合系统，其中耦合包含了惯性耦合、气动耦合及控制量耦合.

2 一种非线性H∞控制方法的全局解

文献［11－12］中为了解决包含非光滑摩擦力的非线性机械模型H∞控制问题，对被控模型做出了很多的假设限制条件.为了借鉴其控制方案设计思路应用于连续光滑的高超声速飞行器非线性姿态跟踪动力学模型，放宽其应用限制条件，对于形如式(2)的光滑非线性耦合系统，做出如下假设为:

假设1 e∈ Rn，u ∈ Rm，w ∈ Rr，z∈ Rl，y∈Rp;

假设 2 f(e)，g1(e)，g2(e)，h1(e)，h2(e)是分段连续函数，且满足局部Lipschitz条件;

假设3 存在反馈控制u使得式(2)渐近稳定.

那么非线性系统式(2)的H∞控制问题表述为:给定正数λ＞0，设计反馈控制器为

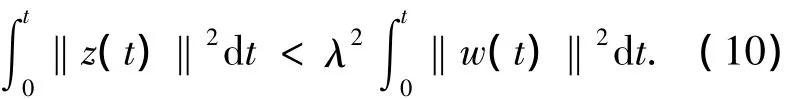
使得对任意给定的t＞0，当初始状态e0=0，初始内状态ξ0=0时，表示为即使得闭环非线性耦合系统式(2)，式(9)的L2增益 ＜λ.这样，如果该系统是零状态可检测的(即当z(t)→0时，e(t)→0成立)，根据La Salla定理可知e0=0是该系统的渐近稳定平衡点［14］.

为了解决上述问题，做出下述2个假设:

假设4 存在平滑正定函数V(e)，使得HJI不等式成立.

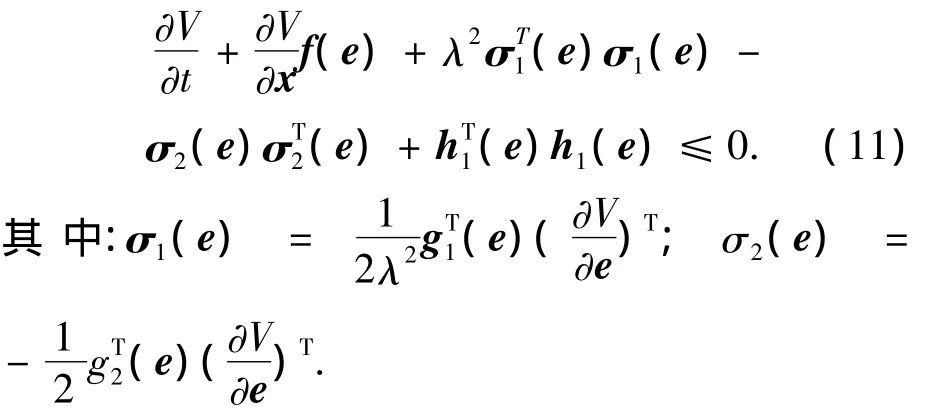
假设5 存在分段连续函数，平滑半正定函数W(e，ξ)且 W(e0，ξ)正定，使得 HJI不等式成立为

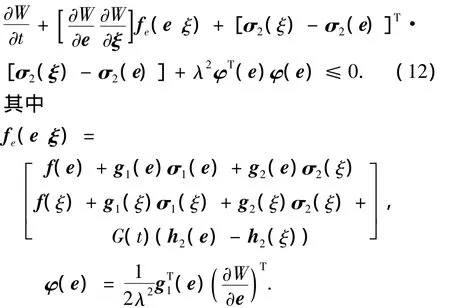
在假设4，5基础上有下列定理:

定理1 若假设4)，5)对于非线性耦合系统式(2)成立，那么存在反馈控制为

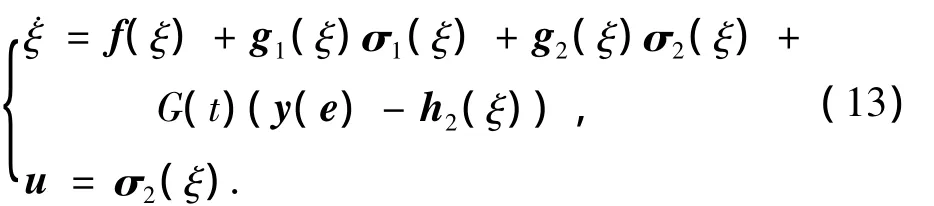
使得非线性耦合系统式(2)全局渐近稳定，闭环系统式(2)，式(9)的L2增益 ＜λ.

证明 首先定义函数为

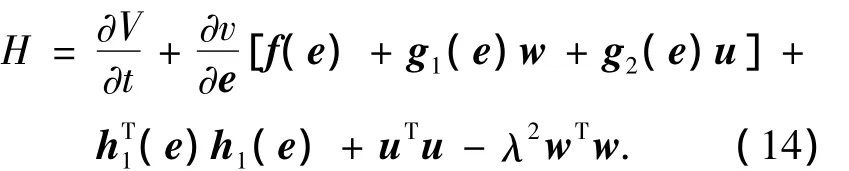
将式(14)分别对w、u求导，得出

将式(14)用泰勒级数展开为

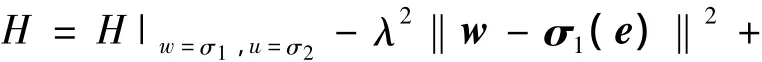
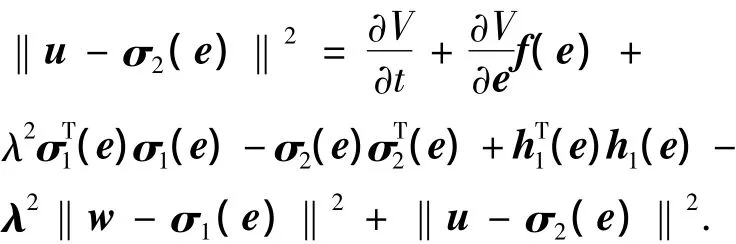
假设4，计算为

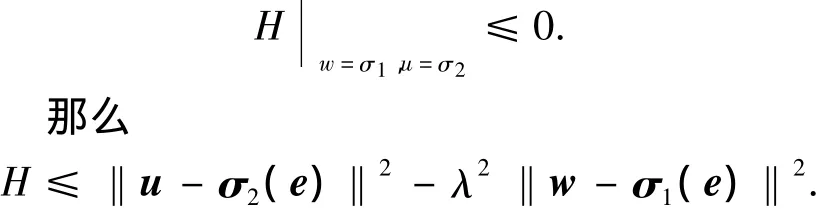
因此得到:

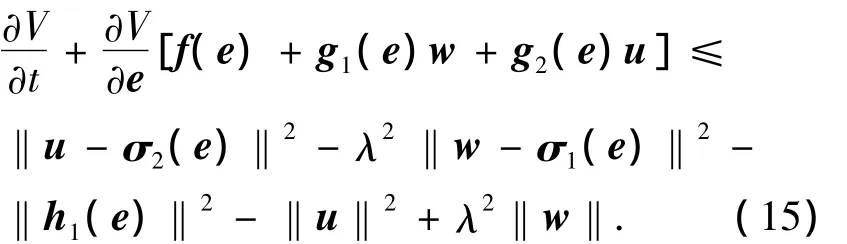
接着，定义函数为

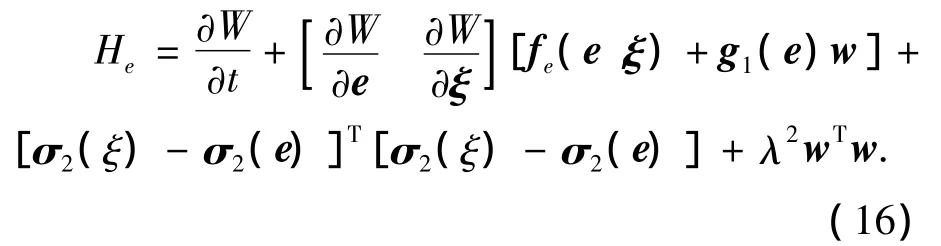
同理可得

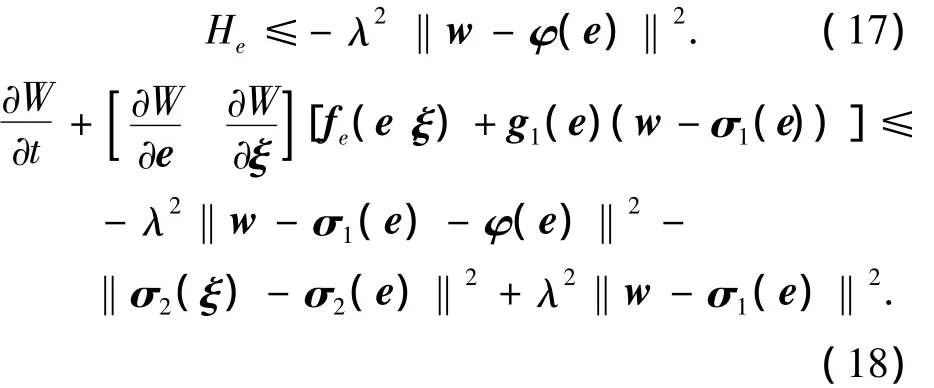
那么构造有界正定函数为

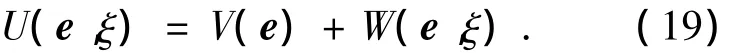
将式(19)对时间t求导为:

1)当w=0，得出

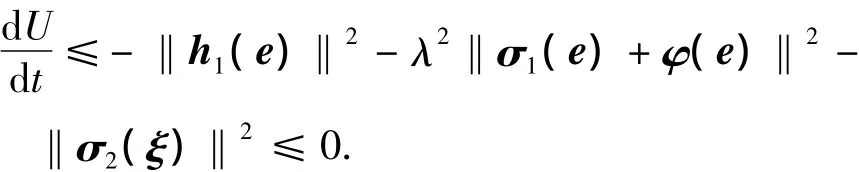
任意给定的t＞ 0，当初始状态(e0，ξ0)=(0，0)时，对式(20)积分得出

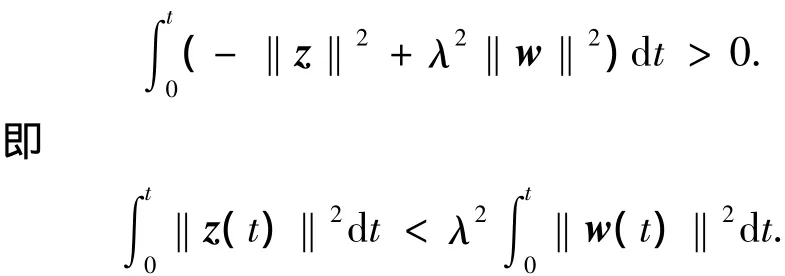
闭环非线性系统式(2)，式(9)渐近稳定.

2)当w≠0，得出

闭环非线性系统式(2)，式(9)的L2增益 ＜λ.

证毕.

因此，式(13)即为上述非线性H∞控制问题的全局解.实际上，在飞行器控制应用中不是必须得到全局解，而只需要在飞行航迹附近的局部空间内使得系统渐近稳定，L2增益 ＜λ即能够满足飞行器飞行要求，这样将大大简化控制器设计的难度.

3 非线性控制的局部状态空间解

若非线性系统式(2)同时满足下述假设:

假设6 对任意给定的t＞0，函数g1(e)，g2(e)，h1(e)，h2(e)在邻近e0=0的局部状态空间内关于e二次连续可微，且在某一给定的局部状态空间内，一阶、二阶导数分段连续且一致有界.

若满足假设6，则在邻近e0=0的局部状态空间内，存在非线性系统式(2)的线性伴随系统为

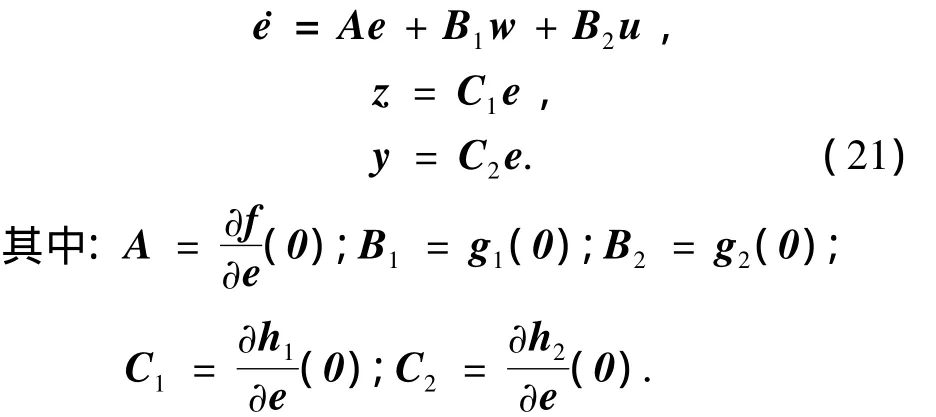
若在邻近e0=0的局部状态空间内，线性伴随系统式(21)满足可稳定可观测条件，那么文献［15］得出了如下结论:

结论1 存在对称半正定矩阵解P使得指数稳定为

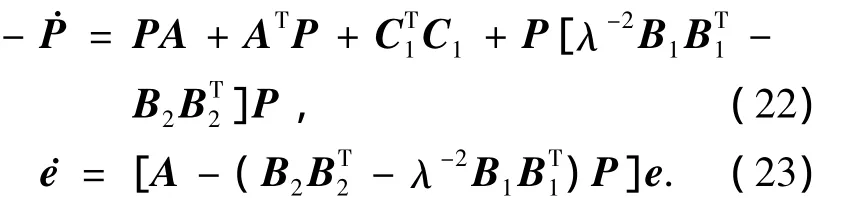
结论2 存在对称半正定矩阵解P使得指数稳定为

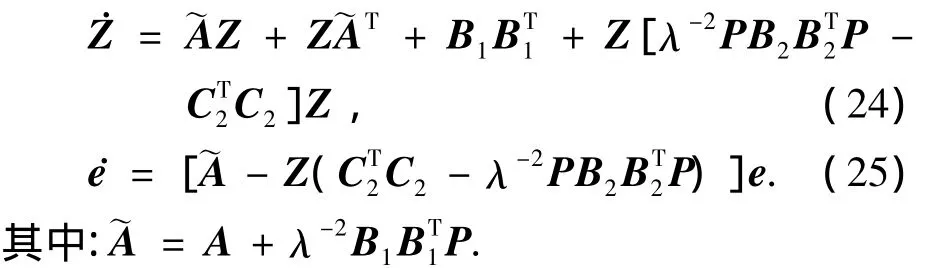
由结论1，2可以得出下列推论:

推论2 存在一个正常数ε0，当ε∈(0，ε0)时，局部伴随线性系统式(21)的Riccati方程存在唯一的有界对称正定解(Pε，Zε)为

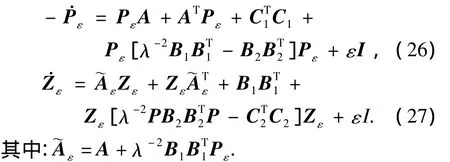
定理3 若满足推论2，那么给定正数常λ＞0，ε＞0，由式(26)，(27)解得有界对称正定解(Pε，Zε)，反馈控制为

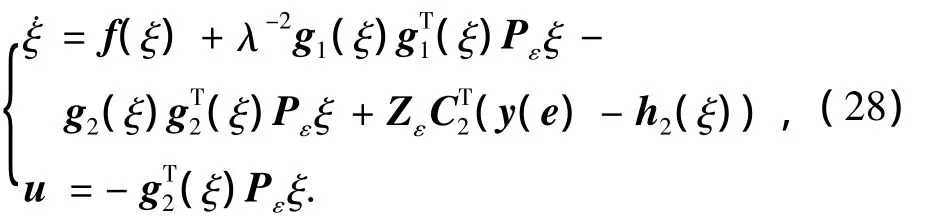
使得闭环非线性系统式(2)，式(28)在邻近(e，ξ)=(0，0)的局部状态空间内渐近稳定、L2增益 ＜λ.

证明 由推论2，在(e，ξ)=(0，0)周围的局部空间，依据假设条件4，5定义如下函数:

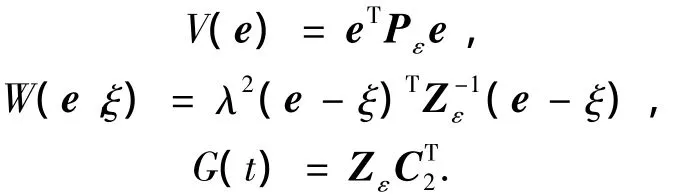
对应HJI不等式式(11)得到:

将式(29)～(33)代入式(11)得到:

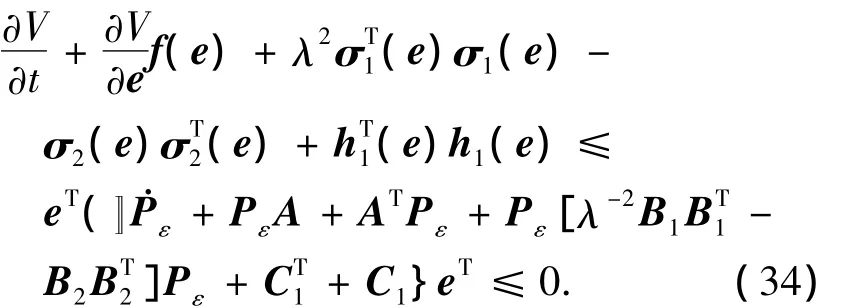
对应不等式HJI式(12)得到:

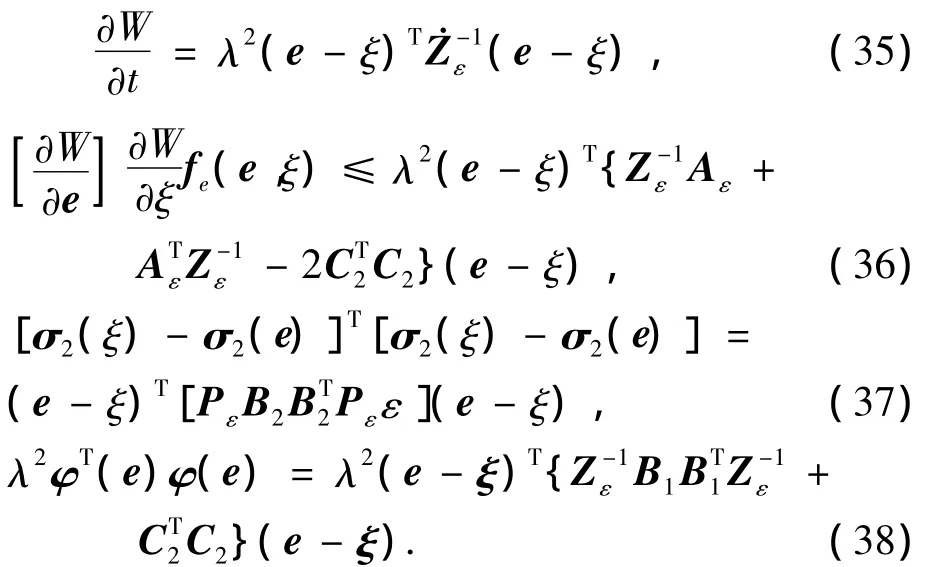
由式(27)得到方程:

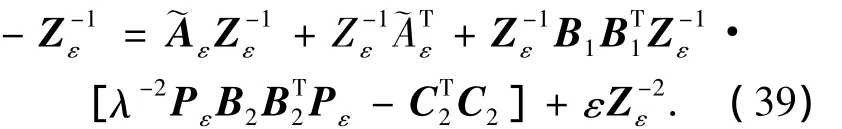
将式(35)～(39)代入式(12)得到:

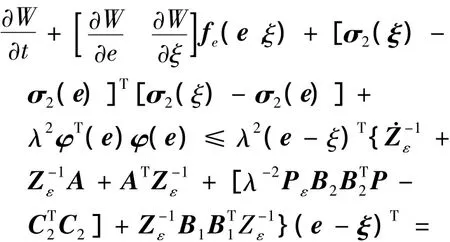
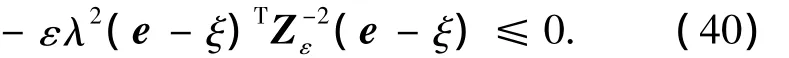
根据定理1，由式(34)，(40)得出反馈控制式(28)是式(2)的非线性H∞控制问题在邻近(e，ξ)=(0，0)的局部状态空间内的局部解.

证毕.

实际应用中，根据高超声速飞行器H∞倾斜转弯姿态跟踪控制系统模型式(2)，在飞行航迹附近的状态空间内，求解邻近指令状态点(e，ξ)=(0，0)的局部状态空间解式(28)，使得闭环非线性系统式(2)，式(28)在上述局部空间内L2增益 ＜λ，系统渐近稳定.

4 仿真结果

选择仿真条件:飞行高度h=50 km，马赫数M=20.应用Matlab软件进行跟踪10°滚转角方波指令、10°攻角方波指令和0°侧滑角指令控制系统仿真验证.仿真中，三通道舵偏与实际中3个舵面舵偏的关系为

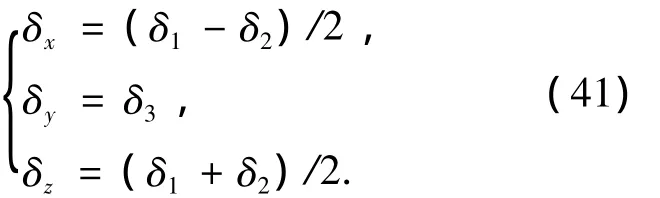
如图1，当从弹身后方沿机体系X轴向前观察时，安装在右翼后缘的右侧升降舵记为δ1，安装在左翼后缘的左侧升降舵记为δ2，安装在垂尾后缘的方向舵记为δ3.左、右升降舵后缘下偏为正偏转，方向舵后缘右偏为正偏转.

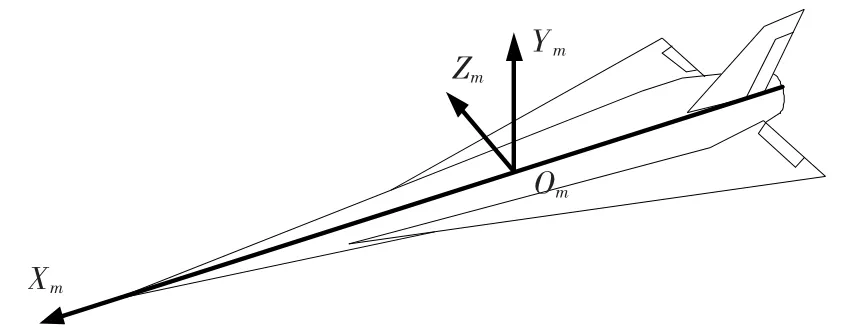
图1 高超声速飞行器

仿真中，假设实际舵系统为二阶环节，舵系统的输入指令与实际输出之间的传递函数为

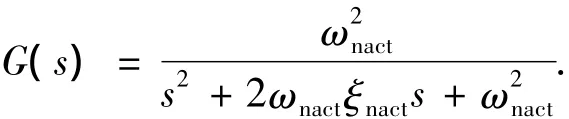
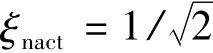
仿真结果如图2～7所示，设计的控制方法满足设计要求:控制系统具有良好的指令跟踪能力，侧滑角β趋近于0°，最大误差 ＜2°;跟踪攻角α方波指令，稳态误差 ＜2%;跟踪滚转角γ稳态误差 ＜1%，γ响应有些缓慢，是因为系统实际舵面控制作用耦合，按照式(41)的实际舵面分配，舵效无法同时使2个通道的跟踪效果达到最优;控制系统具备很好的鲁棒性能，当气动参数摄动±30%时，跟踪控制效果影响很小.

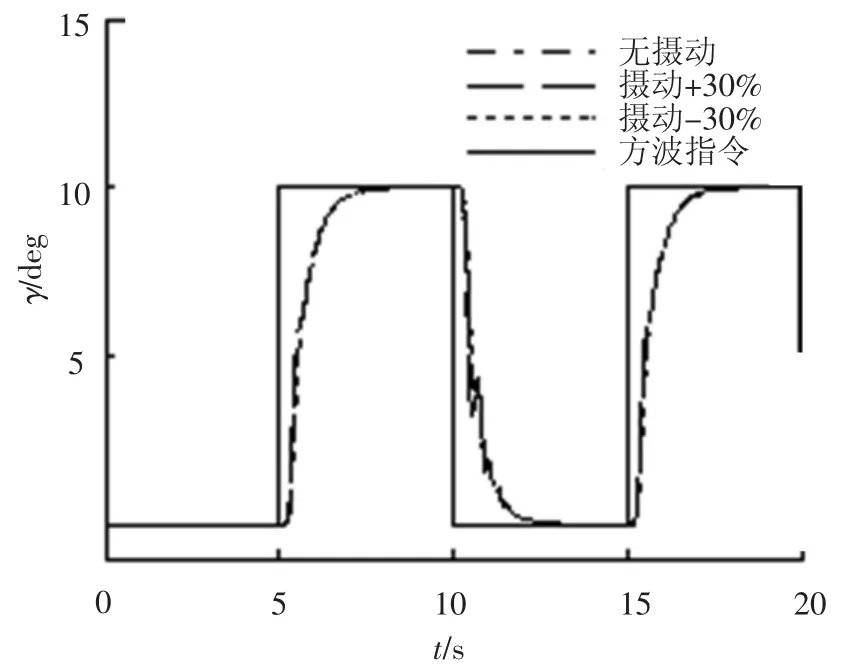
图2 滚转角响应

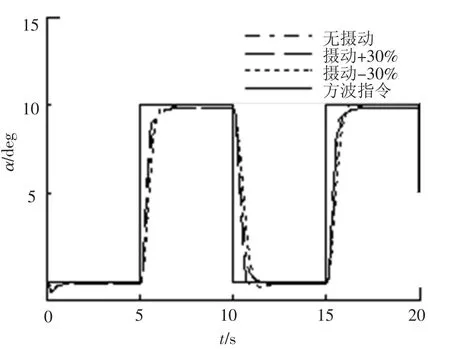
图3 攻角响应

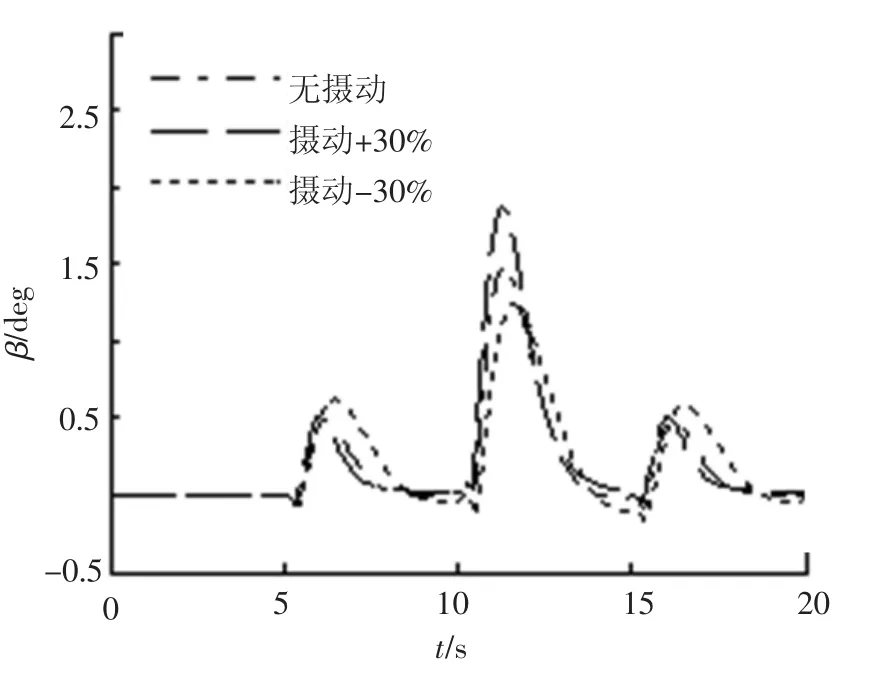
图4 侧滑角响应

实际上，仿真中可实现气动参数摄动±38%时仍有较好的鲁棒性能，当超出这个范围控制结果将发散.即参数摄动＜±38%，系统处于满足本文控制策略的局部状态空间内，参数摄动 ＞±38%，系统就超出了非线性控制器局部状态空间解的设计范围.实际工程中该控制策略在多大范围的局部状态空间内可行，还与具体被控对象模型有关.

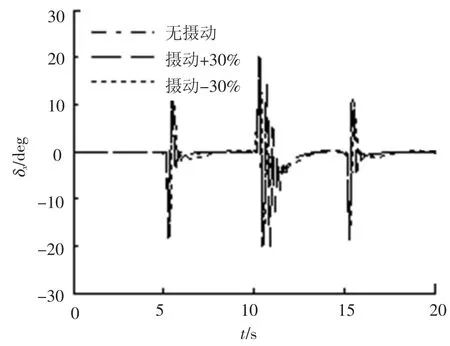
图5 滚转通道舵偏

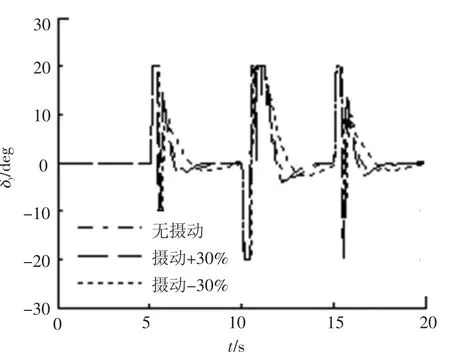
图6 偏航通道舵偏

图7 俯仰通道舵偏

5 结 论

1)针对高超声速飞行器非线性耦合系统姿态跟踪控制问题，建立高超声速飞行器H∞倾斜转弯姿态跟踪控制系统模型，设计非线性H∞姿态跟踪控制器.

2)该方法利用局部空间内伴随系统的Riccati微分方程，避免了非线性H∞控制问题中复杂繁琐的HJI不等式解算过程，便于实际应用.仿真验证了该方法满足性能设计要求，具备较强的鲁棒性能.

［1］GREGORY I M，MCMINN J D，SHAUGHNESSY J D.Hypersonic vehicle control law development using H∞and μ-synthesis［R］.NASA TM －4562，1994.

［2］BUSHCEK H，CALISE A J.Uncertainty modeling and fixed-order controller design for a hypersonic vehicle model［J］.Journal of Guidance，Control，and Dynamics，1997，20(1):42 －48.

［3］LOHSOONTHORN P，JONCKHEERE E，DALZELL S.Eigenstructure vs constrained Hxdesign for hypersonic winged cone ［J］.Journal of Guidance，Control，and Dynamics，2001，24(4):648 －658.

［4］HELLER M，SACHS G.Flight dynamics and robust control of a hypersonic test vehicle with ramjet propulsion［C］//AIAA International Space Planes and Hypersonic Systems and Technologies Conference.Norfolk:AIAA，1998:126－136.

［5］JENNIFER G，JOHN V.Selection of longitudinal desired dynamics for dynamic inversion controlled re-entry vehicles［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.USA:AIAA，2001:1－11.

［6］XU H J，IOANNOU P A，MIRMIRANI M.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance，Control and Dynamics，2004，27(5):829－838.

［7］WANG Q，STENGEL R F.Robust nonlinear control of a hypersonic aircraft［J］.Journal of Guidance，Control and Dynamics，2000，23(4):577 －584.

［8］BRINKER J S，WISE K A.Stability and flying qualities robustness of a dynamic inversion aircraft control law［J］.Journal of Guidance，Control and Dynamics，1996，19(6):1270－1277.

［9］ISIDORI A，ASTOLFI A.Disturbance attenuation and H∞－control via measurement feedback in nonlinear systems［J］.IEEE Transactions Automatic Control，1992，37(9):1283－1293.

［10］Van Der SCHAFT A J.L2－gain analysis of nonlinear systems and nonlinear state feedback H∞control［J］.IEEE Transactions on Automatic Control，1992，37(6):770－784.

［11］ORLOV Y，ACHO L，SOLIS V.Nonlinear H∞－control oftime-varying systems［C］//Proceedings of the 38th conference on decision and control.Canada:AIAA，1999:3764－3769.

［12］AGUILAR L T，ORLOV Y，ACHO L.Nonlinear H∞－control of nonsmooth time-varying systems with application to friction mechanical manipulators［J］.Automatica，2003，39(7):1530－1542.

［13］彭冠一.防空导弹制导控制系统设计［M］.北京:宇航出版社，1996:236－240.

［14］梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京:清华大学出版社，2003:172－182.

［15］RAVI R，NAGPAL K，KHARGONEKAR P.H∞control of linear time-varying systems［C］//Proceedings of the 29th Conformer on Decision and Control.USA:AIAA，1990:1796－1801.

Design of nonlinear H∞controller for hypersonic vehicle system

WANG Yan，ZHOU Feng-qi，ZHOU Jun，GUO Jian-guo

(Institute for Precision Guidance and Control，Northwestern Polytechnical University，710072 Xi'an，China，wangyan991926@sina.com)

For the BTT attitude tracking control problem of hypersonic vehicle，a state-error-space implementation expression of nonlinear H∞attitude tracking control for above nonlinear coupling system is given firstly.Then basing on γ－energy-dissipation and L2gain performance criterion in nonlinear system theory，the smooth differentiable stored-energy function is designed，which subject to the Hamilton-Jacobi-Isaacs inequality.Following some assumptions，a local state-space solution of nonlinear H∞attitude-tracking control problem for nonlinear coupling hypersonic vehicle system is obtained，by using Riccati differential equation of linear following system in local state-space.The local state-space is the neighborhood around the command state error space.Above approach avoids complicated solving process of Hamilton-Jacobi-Isaacs inequality，thus it's a good reference for engineering.

hypersonic vehicle;nonlinear H∞control;L2gain;Hamilton-Jacobi-Isaacs inequality

V44

A

0367－6234(2011)09－0128－06

2011－06－02.

航天科技创新基金资助项目(N11XW0001).

王 延(1979—)，男，博士研究生;

周凤岐(1935—)，男，教授，博士生导师;

周 军(1966—)男，教授，博士生导师.

(编辑 张 红)