预应力混凝土组合箱梁扭后抗弯性能分析

胡少伟，胡汉林

(南京水利科学研究院，江苏 南京 210029)

目前，预应力混凝土组合箱梁在桥梁工程中得到了广泛应用［1］.由于该结构发挥了钢材和混凝土各自的材料优势，且钢箱梁抗扭、抗弯性能好［2－6］，预应力技术又提高了梁结构的强度与刚度［7－9］，所以预应力混凝土组合箱梁在城市大跨桥梁中的应用前景越来越广阔.工程实际中桥梁通常处于弯矩、扭矩等共同作用下的复合受力状态，而且不同的荷载组合对预应力混凝土组合箱梁的承载性能影响很大，因此探讨组合梁受扭后的承载能力具有现实意义.

为了研究预应力混凝土组合箱梁扭后抗弯性能，完成了5根预应力组合梁的先扭后弯试验.试验在梁跨中对称荷载作用下进行，考虑试验梁受扭矩作用历史，并与完整预应力组合梁的试验进行对比得到扭后预应力组合梁的极限抗弯承载力、跨中弯矩－挠度曲线、钢梁截面应变增长曲线等重要参数，并提出了预应力组合梁扭后承载力计算公式.

1 试验情况

试验设计了5根跨度为3.3 m的预应力混凝土组合箱梁，在抗弯试验前，2根试验梁已受纯扭荷载达到破坏，3根梁已受复合弯扭荷载达到破坏.试验梁混凝土采用C60高强混凝土.钢箱梁采用Q235钢板焊接组成，托板和底板采用10 mm钢板，腹板采用8 mm中板.栓钉按照塑性方法、完全剪力连接设计，直径为16 mm，间距120 mm，沿纵向双排均匀布置，以保证钢与混凝土截面间剪力的有效传递.各构件截面形状、尺寸完全相同.梁截面尺寸见图1，试验梁材料特性见表1.

图1 试验梁截面(单位:mm)Fig.1 Details of specimen section(unit:mm)

表1 混凝土和钢材的力学性能Tab.1 Mechanical performance of concrete and steel

1.1 试验梁受扭破坏情况

5根试验梁在纯弯试验之前，均受扭破坏，受扭情况为:2根纯扭破坏，3根受复合弯扭破坏(破坏类型为扭型破坏).试验在自行设计的加载装置上进行，采用液压伺服机控制，对称分级加载直至破坏.纯扭试验装置和复合弯扭试验装置分别见图2和3，抗扭试验参数见表2.

纯扭及弯扭试验结果见表3.从表3可以看出，由于弯矩作用，受弯扭作用试验梁开裂时的转角比受纯扭作用梁要大，而极限转角却较小，证明弯矩的作用提高了组合梁的抗扭刚度.弯扭作用下的梁扭转破坏表现出脆性，而纯扭梁表现出一定的延性.

图2 纯扭试验装置Fig.2 Loading apparatus with pure torque

图3 弯扭试验加载装置Fig.3 Loading apparatus with bending-torsion

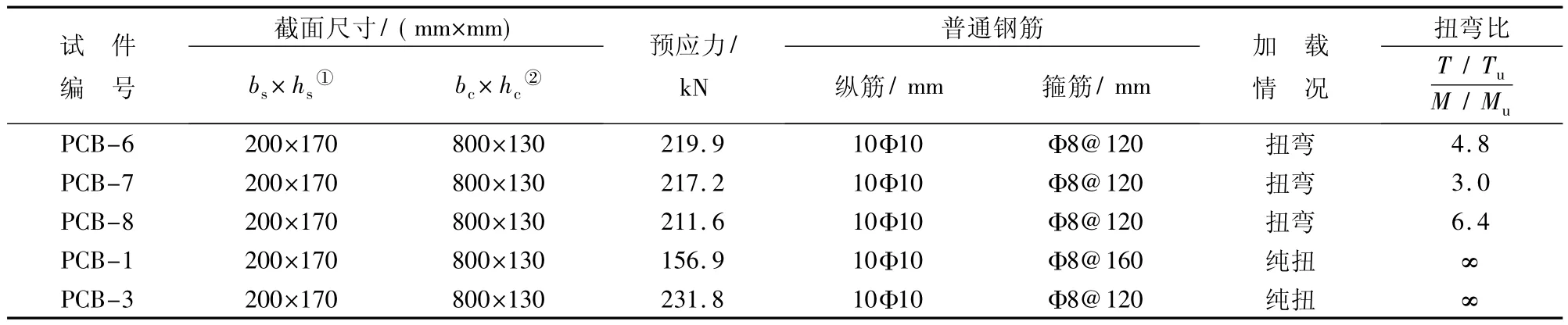
表2 抗扭试验梁主要参数Tab.2 Main parameters of specimens

表3 纯扭、弯扭试验结果Tab.3 Main experimental results with pure torsion or bending-torsion

不论是纯扭还是复合弯扭，试验梁破坏过程大致如此:加载初期，翼板表面未出现裂缝;随着扭矩的逐渐增加，靠近固定端混凝土翼板上表面中部首先出现与梁纵轴成30°～40°斜向裂缝;随着扭矩的继续增大，斜裂缝逐渐向两侧边扩展延伸，斜裂缝的数量不断增加，混凝土翼板的下表面也开始出现斜裂缝并向两侧开展，直至2个短侧边出现开裂，上下表面的斜裂缝彼此贯通，翼板4个侧面上形成近似平行、断断续续、前后交错的环绕整个翼板的近似螺旋形裂缝;最后，由于混凝土翼板出现1条或2条宽度较大的主斜拉裂缝导致组合梁受扭破坏.图4和5分别为钢梁荷载应变和试验梁破坏时裂缝情况.

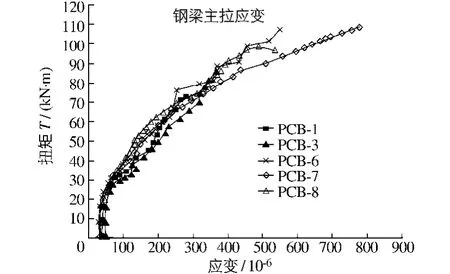
图4 钢梁荷载应变曲线Fig.4 Load-strain curve of steel beam

图5 纯扭、弯扭试验梁破坏时裂缝发展过程(单位:尺寸为cm，扭矩为kN·m)Fig.5 Crack development of specimens owing to the failure of torsion and bending-torsion

从图4可见:5根试验梁受到扭矩作用破坏时，钢梁仍然处于弹性阶段，最大应变约为800×10－6，远未达到屈服，因此，试验梁的破坏由混凝土的抗扭能力控制.从图5可见:纯扭梁和弯扭梁达到破坏状态时，混凝土破坏程度不尽相同，纯扭梁的裂缝数量要多于弯扭梁.

1.2 扭后梁的纯弯试验

5根试验梁在扭型破坏后对其重新进行张拉预应力试验，采用直线型布筋形式.为考察预应力对扭后梁承载能力的增强效果，分别对PCB－6，PCB－8和 PCB－1施加200 kN的预应力，对 PCB－7，PCB－3施加240 kN的预应力.为了防止梁在偏心受力下产生较大扭矩引起开裂，张拉分级分侧进行，每束张拉分5～6级完成.考虑锚具变形、锚具与端板之间的缝隙被挤紧，以及千斤顶卸载时夹片在锚具内滑移使得被拉紧的钢绞线内缩会导致较大的预应力损失，因此进行一定程度的超张拉.采用液压伺服千斤顶在梁的三分点对称加载，加载装置见图6.试验数据利用东华DH－3816静态应变采集系统采集.

由于混凝土表面已开裂，所以试验全过程实时监测钢梁应变、预应力筋应变、交界面相对滑移、组合梁挠度变形，而不考虑混凝土应变情况.

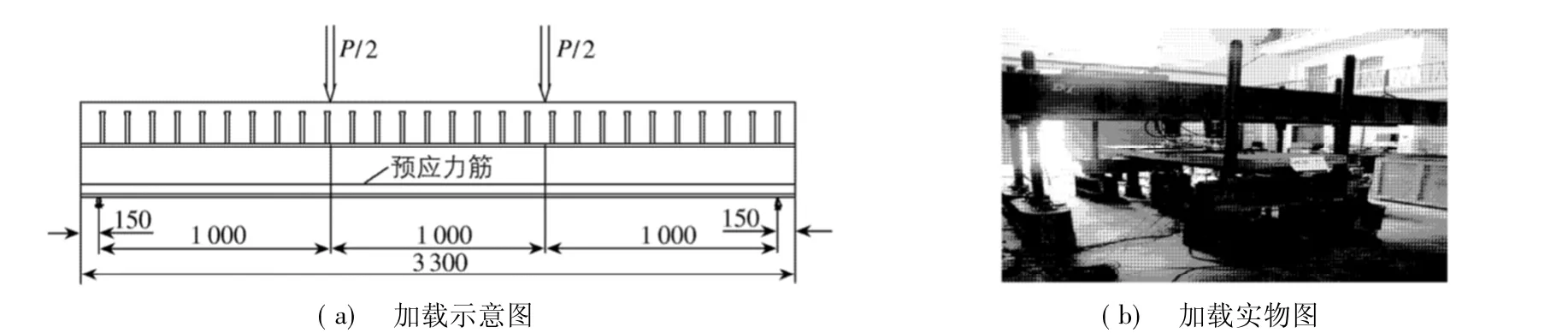
图6 纯弯试验装置(单位:mm)Fig.6 Loading apparatus with bending

1.2.1 试验梁破坏特征 扭后梁的纯弯试验过程为:在加载初期，钢梁底部应变及跨中挠度处于线性增长阶段;随着荷载的增加，受拉区混凝土扭型裂缝逐渐开展，裂缝逐渐变宽，同时应变出现较快增长;当钢梁底板屈服后，钢梁应变出现非线性增长，挠度增长加快，原有裂缝逐渐变长变宽，同时新的弯型裂缝逐渐变多;接近极限荷载时，腹板大部分已经屈服，混凝土翼板顶部有起皮现象，挠度增长很快;最后达到极限荷载时，梁顶部混凝土在跨中区域或者在加载点处被压碎，从而导致结构破坏，破坏位置与受扭破坏时最大裂缝相关.试验梁破坏情况见图7.

图7 试验梁混凝土翼板破坏Fig.7 Failure pattern of concrete flange of specimens

1.2.2 试验应变、挠度、滑移分析 为了考察扭后梁与完整梁不同的抗弯特征，对比分析纯扭梁PCB－1，弯扭梁PCB－8和完整梁PCB－4的应变与挠度.图8为跨中钢梁底板拉应变增长曲线，图9为荷载－跨中挠度曲线.

从图8可见:PCB－1的应变增长要快于PCB－8和PCB－4，且在同一级荷载条件下，PCB－1的应变值最大，PCB－4的应变值最小，说明受扭破坏后，试验梁的抗弯截面模量会减小，纯扭破坏梁的减小程度高于弯扭破坏梁，因此PCB－4与PCB－8钢梁屈服弯矩较为接近，而PCB－1屈服弯矩降低很多.从图9可见:弹性阶段时，在相同荷载作用下，纯扭梁PCB－1的挠度要大于弯扭梁PCB－8和完整梁PCB－4，而PCB－8与PCB－4的挠度相差不大，说明纯扭梁的刚度较之完整梁要低，而弯扭梁的刚度没有降低.PCB－1梁的弹性终点最低，PCB－8稍高，但均低于PCB－4的弹性终点，接近极限荷载时，扭后梁的弯矩－挠度曲线斜率较小，几乎接近于水平，说明荷载增加不大而挠度增长很快，表现出一定的脆性.

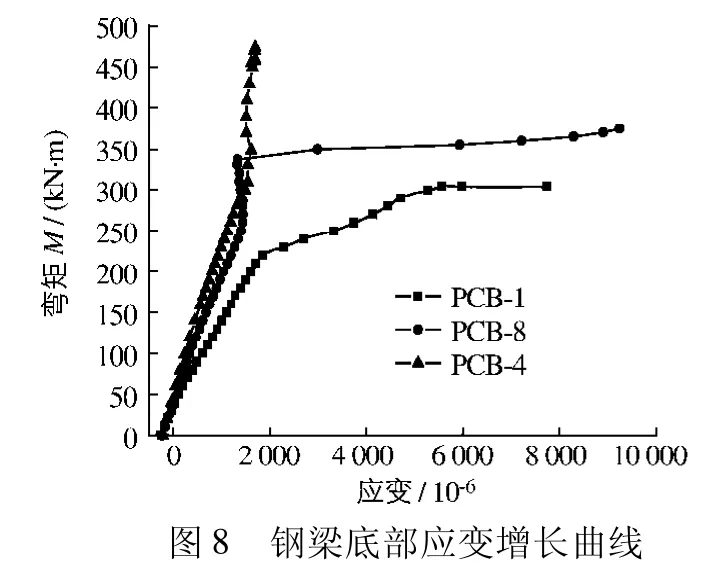
图8 钢梁底部应变增长曲线Fig.8 Comparison of strain increases in bottom of steel beams

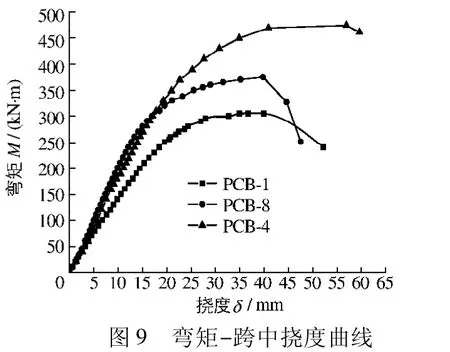
图9 弯矩－跨中挠度曲线Fig.9 Curves of moment-deflection at midspan

为考察预应力等级对扭后梁极限抗弯承载能力的提高作用，对比分析PCB－1和PCB－3的应变与挠度.图10为PCB－1和PCB－3的钢梁底部应变增长曲线，图11为PCB－1和PCB－3的弯矩－跨中挠度曲线.

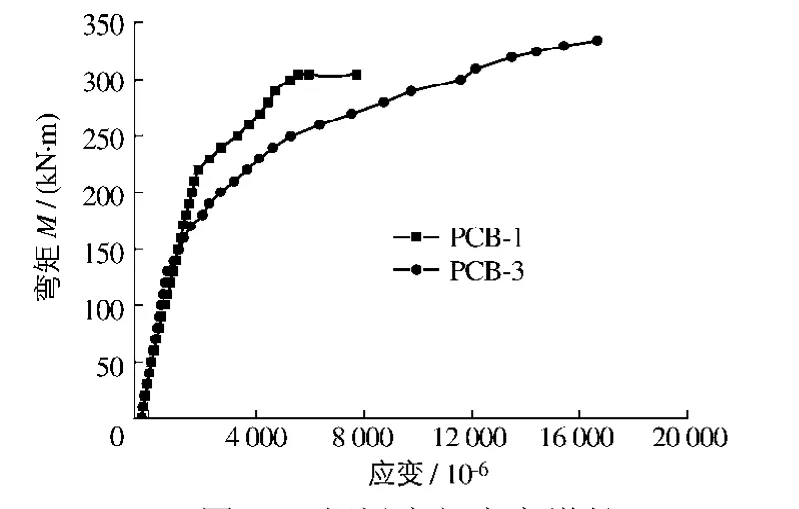
图10 钢梁底部应变增长Fig．10 Increases of strain in bottom of steel beams

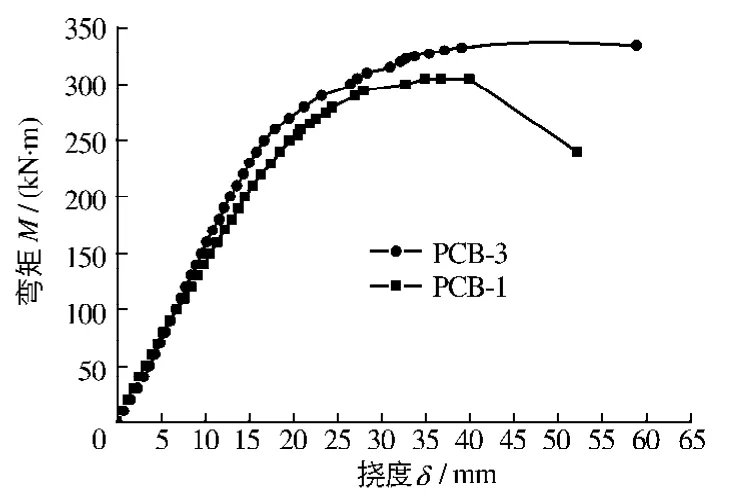
图11 弯矩－跨中挠度曲线Fig.11 Curve of moment-deflection at midspan

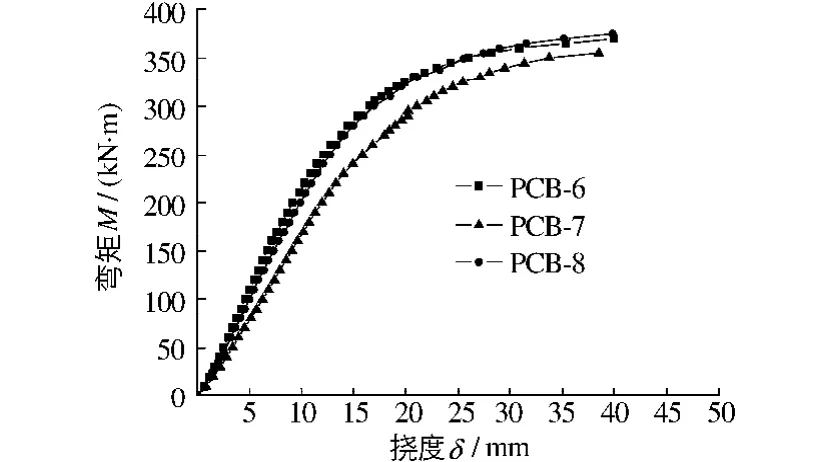
图12 弯矩－跨中挠度曲线Fig.12 Curves of moment-deflection at midspan

从图10可见，对于相同荷载下的钢梁屈服前PCB－3的应变略小于PCB－1;屈服后，应变的增长出现不规律性，PCB－3的较快，PCB－1的较缓慢.从图11可见，由于初始预应力较大，在弹性阶段，PCB－3的弯矩－挠度曲线斜率要大于PCB－1，即在相同荷载下，PCB－3的挠度要大于PCB－1.可见，提高初始预应力值能够提高梁的抗弯刚度，改善梁的抗弯特性.同时，PCB－3破坏时的挠度要大于PCB－1，证明其延性要好于后者.

为考察扭弯比对扭后抗弯特性的影响，图12分析了弯扭梁的荷载－挠度曲线.

从图12可见，3根弯扭梁弯矩－挠度曲线符合组合梁破坏的一般规律:弹性阶段－非线性阶段－破坏阶段;其中PCB－6和PCB－8两根弯扭梁的荷载－跨中挠度曲线类似，证明扭弯比大于4.8后，即梁在弯扭破坏时的弯矩若很小，则梁的抗弯刚度和强度相差不大.PCB－7梁尽管初始预应力等级要高于PCB－6和PCB－8，但是其刚度仍然较小，强度也较低，说明在扭弯比较小时发生弯扭破坏，若弯矩较大(PCB－7的弯矩接近纯弯梁PCB－4的屈服弯矩)，则梁的刚度和强度会减小许多.

图13为5根扭后梁的预应力随荷载增长情况.在相同荷载条件下，PCB－1的预应力增量最大，PCB－6，PCB－7和 PCB－8增长情况在弹性阶段相差不大，而PCB－3由于初始预应力较大，其预应力增量要小于PCB－1，与弯扭梁情况接近.这些结论说明:预应力增量与梁的刚度有关，在相同的荷载条件下，梁的刚度越大，变形越小，则预应力钢绞线变形小，导致增量小.同时，从图13也可看出，预应力钢绞线增量经历了线性阶段和非线性的阶段，从侧面反映了梁的变形情况.

1.2.3 纯弯试验结果分析 纯弯试验结果见表4，表中PCB－4为完整纯弯试验梁，与扭后纯弯试验进行对比.

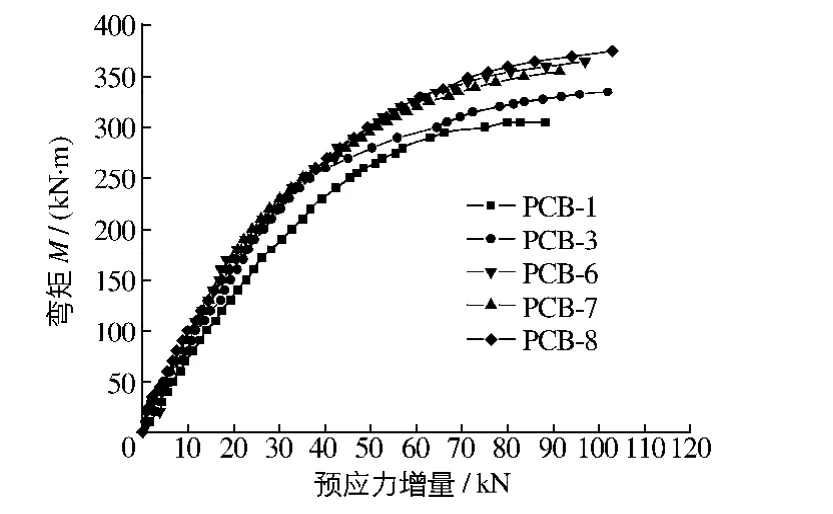
图13 弯矩－体外预应力增量曲线Fig.13 Curves of moment-stress in external tendon

表4 纯弯试验结果Tab.4 Main experimental results with pure bending

从表4可见:(1)在相同预应力等级的情况下，受纯扭破坏试验梁(PCB－1)其抗弯承载能力只有完好试验梁(PCB－4)抗弯承载能力的64%，挠度只有61%;而受弯扭破坏试验梁(PCB－8)其抗弯承载能力达完好试验梁(PCB－4)抗弯承载能力的79%，挠度达70%.(2)从PCB－1和PCB－3的结果可以看出，初始预应力的提高有利于受扭破坏梁的极限承载能力的提高.(3)复合受扭破坏试验梁其扭后抗弯承载能力与扭弯比有关.当扭弯比较大时(PCB－6与PCB－8)，即受弯扭破坏，弯矩值不太大时，其扭后抗弯承载能力相差不大;而当扭弯比较小时(PCB－7)，其扭后抗弯承载能力会较低.(4)对于本试验采用的直线型无转向块的布筋方式，预应力筋增量与梁的强度和刚度相关.

2 预应力组合梁受扭破坏后的极限抗弯承载能力计算

目前，对于组合梁、预应力组合梁的极限抗弯承载能力计算，多采用简化的塑性理论计算方法［10－13］和弹塑性计算理论［14－16］.组合梁在承受扭矩时，一般假设混凝土翼板与钢梁单独承担一定扭矩，栓钉等连接件保证混凝土翼板和钢梁的变形协调.根据空间变角桁架模型，混凝土翼板可以将其假想为一个壁厚为t的箱形截面构件，当承受扭矩时，沿箱壁产生环形的剪力流，当混凝土开裂后，可以将翼板比拟为以纵筋为弦杆，箍筋为竖杆，混凝土为斜压腹杆的空间桁架［17－19］.因此当扭矩受扭破坏后，作为斜压腹杆的混凝土部分已经压碎破坏.扭后组合梁在承受弯矩时，假设斜压腹杆部分混凝土已压坏不承担任何荷载，只考虑核心混凝土的承压作用，因此可以对混凝土翼板进行折减.对于纯扭破坏情况，根据文献［20］有效壁厚可取:te=h/3，其中h为混凝土翼板的高度.

对于复合弯扭破坏情况，弯矩的存在使混凝土顶部纵筋拉应力减小，从而提高了混凝土翼板的抗扭能力.根据试验梁受扭破坏情况可知，受弯扭破坏梁的混凝土破坏程度要低于受纯扭破坏梁.结合试验弯扭梁的有效壁厚可取混凝土的保护层厚度，即te=20 mm.

从试验受弯破坏情况看，由于混凝土翼板尺寸的折减，梁的转动能力降低，导致钢梁顶板到破坏时应变仍较小，因此在计算过程中可以不考虑钢梁顶板对抗弯承载能力的贡献.

本文采用简化塑性理论，并结合试验，考虑扭型破坏对混凝土翼板尺寸的折减作用，来计算预应力组合梁受扭破坏后的极限抗弯承载力.对于完全剪力连接预应力组合梁，极限抗弯承载能力的计算简图见图14.

图14 抗弯承载能力计算简图Fig.14 Calculation diagram of bending capacity

根据力的平衡条件:

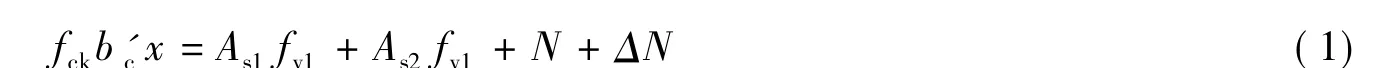
式中:fck为混凝土抗压强度;b'c为混凝土翼板折减后的宽度，取b'c=bc－2te;As1，As2分别为钢梁腹板、底板的截面面积;fy1，fy2，分别为腹板、底板的屈服强度;N，ΔN分别为预应力筋的初始预应力和预应力增量.则可得混凝土受压区高度:

根据力矩平衡条件，可得抗弯承载能力为:

式中:y1，y2分别为受拉区钢梁腹板、钢梁底板截面形心到混凝土翼板受压区截面形心的距离，y3为考虑二次效应后的预应力筋截面形心到混凝土翼板受压区截面形心的距离.

预应力增量Δ 的取值与布筋形式及梁的强度 刚度有关 对于本试验的无转向块的直线型布筋 钢梁强度大，则预应力增量大，钢梁刚度大，则预应力增量小.从试验结果看，ΔN的取值大约为0.5 N.

将试验梁数据代入式(2)和(3)进行计算，并与试验结果进行比较(见表5).从表5可见，计算值和实测值吻合较好，大部分计算值小于实测值，说明式(3)用于计算预应力组合梁受扭破坏后的极限承载力是可行的.但是式(3)仍存在如下不足:(1)对于复合弯扭破坏后的试验梁，有效壁厚的取值没有考虑扭弯比的影响;(2)预应力增量ΔN的取值与梁变形有关，对于受扭破坏后的预应力组合梁刚度未予分析，因此ΔN简单地取为0.5 N，计算值取实测值.

表5 抗弯承载力试验实测值与计算值的比较Tab.5 Comparison between the calculated and measured values of the bending capacity

3 结语

(1)预应力组合梁受扭破坏后仍保留一定的抗弯承载能力，受扭破坏梁的弹性终点均低于完整试验梁，达到弹性终点后，受扭破坏梁的塑性阶段较短，破坏时表现出一定的脆性.

(2)受扭破坏梁在抗弯破坏时，混凝土破坏较为迅速，梁的转动能力降低，导致钢梁全截面没有达到完全屈服.

(3)初始预应力的提高可以增强受扭破坏梁的抗弯承载能力，在组合梁钢箱梁上施加的纵向预应力，通过栓钉连接件向混凝土翼板中传递，预应力的传递沿梁全跨存在，组合梁预应力段越长，预应力传递的截面剪力分布越均匀.

(4)对于受扭破坏梁的抗弯承载能力计算，考虑组合梁混凝土翼板尺寸的折减是可行的.式(3)能够较好地计算预应力组合梁受扭破坏后的极限承载能力，但是扭弯比对有效厚度的影响仍需要研究.

［1］胡少伟.组合梁抗扭分析与设计［M］.北京:人民交通出版社，2005:155-159.(HU Shao-wei.Torsional analysis and design of composite steel-concrete beams［M］.Beijing:China Communication Press，2005:155-159.(in Chinese))

［2］夏文敏，刘雪梅.钢－混组合梁的研究现状与展望［J］.四川建筑，2010，30(2):45-47.(XIA Wen-min，LIU Xue-mei.The research status and prospect of steel-concrete composite beams［J］.Sichuan Architecture，2010，30(2):45-47.(in Chinese))

［3］尧国皇，林松，陈宜言.钢箱－混凝土组合梁抗弯力学性能研究［J］.特种结构，2010，27(2):77-78.(YAO Guo-huang，LIN Song，CHEN Yi-yan.Research on behavior of steel box-concrete composite beam subjected to bending［J］.Special Structures，2010，27(2):77-78.(in Chinese))

［4］吴兴邦.钢－混凝土组合梁的研究与发展［J］.科技信息，2007(11):341.(WU Xing-bang.Development and research of composite steel-concrete beams［J］.Science ＆ Technology Information，2007(11):341.(in Chinese))

［5］李波.钢－混凝土组合结构发展趋势探析［J］.吉林建筑工程学院学报，2010，27(2):36-37.(LI Bo.The development trend of the steel-concrete composite structure［J］.Journal of Jilin Institute of Architecture＆ Civil Engineering，2010，27(2):36-37.(in Chinese))

［6］武岩，刘广杰.钢－混凝土组合结构的发展与应用［J］.山西建筑，2007(14):60-61.(WU Yan，LIU Guang-jie.Development and application of steel-concrete combined structure［J］.Shanxi Architecture，2007(14):60-61.(in Chinese))

［7］赵静，蔡建林.外包钢－混凝土组合梁受扭性能［J］.土木建筑与环境工程，2009，31(5):103-104.(ZHAO Jing，CAI Jian-lin.Torsion behavior of steel-encased concrete composite beams［J］.Journal of Ciril，Architectural and Environmental Engineering，2009，31(5):103-104.(in Chinese))

［8］胡少伟，陈亮，游日.组合桥梁抗扭性能研究综述及其进展［C］∥第二届结构工程新进展国际论坛论文集.大连:中国建筑工业出版社，2008:661-669.(HU Shao-wei，CHEN Liang，YOU Ri.Research overview and perspective on torsional behavior of steel-concrete composite bridges［C］∥Proceedings of the Second International Forum on Advances in Structural Engineering.Dalian:China Architecture and Building Press，2008:661-669.(in Chinese))

［9］钟新谷，舒小娟，沈明燕，等.钢箱－混凝土组合梁弯曲性能试验研究［J］.建筑结构学报，2006，27(1):122-124.(ZHONG Xin-gu，SHU Xiao-juan，SHEN Ming-yan，et al.The behavior of composite steel-concrete beams of bending properties［J］.Journal of Building Structures，2006，27(1):122-124.(in Chinese))

［10］聂建国，唐亮，胡少伟，等.钢－混凝土组合箱梁的抗扭强度［J］.土木工程学报，2008，41(1):1-11.(NIE Jian-guo，TANG Liang，HU Shao-wei，et al.Torsional strength of steel-concrete composite box girders［J］.China Civil Engineering Journal，2008，41(1):1-11.(in Chinese))

［11］胡少伟，聂建国，熊辉.钢－混凝土组合梁的受扭试验与分析［J］.建筑结构学报，2006，27(4):103-109.(HU Shaowei，NIE Jian-guo，XIONG Hui.Torsional experiment and analysis on composite steel-concrete beams［J］.Journal of Building Structures，2006，27(4):103-109.(in Chinese))

［12］胡少伟，聂建国，朱林森.钢－混凝土复合弯扭作用下非线性分析［J］.工程力学，2005，22(2):1-5，26.(HU Shaowei，NIE Jian-guo，ZHU Lin-sen.Nonlinear analysis of composite steel-concrete beams under combined flexure and torsion［J］.Engineering Mechanics，2005，22(2):1-5，26.(in Chinese))

［13］陈亮.预应力组合箱梁受扭与复合弯扭性能试验研究［D］.南京:南京水利科学研究院，2009.(CHEN Liang.Experimental study on the performance of prestressed composite box beams under pure torsion and combined bending and torsion［D］.Nanjing:Nanjing Hydraulic Research Institute，2009.(in Chinese))

［14］LORENC W，KUBICA E.Behavior of composite beams prestressed with external tendons:Experimental study［J］.J Constr Steel Res，2006，62:145-148.

［15］RANZI G，BRADFORD M A.Analytical solutions for the time-dependent behavior of composite beams with partial interaction［J］.Int J Solids Struct，2006，43(1):71-74.

［16］DEZI L.Shrinkage effects in composite beams with flexible connection［J］.Journal of Construction ＆ Steel Research，1994，28(3):321-324.

［17］XUE Wei-chen，DING Min，HE Chi，et al.Long-term behavior of prestressed composite beams at service loads for one year［J］.Struct Engrg，2008，6:221-224.

［18］CHEN Shi-ming.Load carrying capacity of composite beams prestressed with external tendons under positive moment［J］.Journal of Constructional Steel Research，2005，61:515-530.

［19］AMIN HEIDARPOUR，MARK ANDREW BRADFORD.Improved flexural-torsional stability analysis of thin-walled composite beam and exact stiffness matrix［J］.International Journal of Mechanical Sciences，2007，49(8):56-58.

［20］LAWTHER R，GILBERT R I.Deflection analysis of composite structures using the rate of creep method［J］.Structural Engineer，1992，70(12):113-115.