排气消声器拉深成形的压边力优化

张燕琴

0 引言

压边力是影响薄板冲压成形的一个重要工艺参数。一般来说，压边力过小，板料容易失稳起皱；而压边力过大则拉裂的趋势会明显增加[1]。在复杂的薄板成形过程中传统恒定压边力控制往往难以同时避免起皱、厚度减薄量过大和开裂这几种缺陷，为此一些学者提出了变压边力控制方法[2]，即在薄板成形过程中，压边力大小随凸模行程变化而变化的一种加载方式。作为改善冲压件成形质量的一种有效控制手段，变压边力控制技术日益受到关注。变压边力的优点是可以充分利用材料的成形性能提高零件的成形质量，缺点是为工艺设计增加了难度[3]。单纯依赖试验，通过“试错”来获得压边力控制曲线效率很低，通过数值仿真也只是将“试错”移到计算机中，不能有效提高效率。

近年来，人工智能技术被引入压边力控制领域[4]。板料成形过程是高度非线性的过程，在进行压边力优化设计时，选用何种优化算法是关键。RBF神经网络由于具有非线性逼近能力强、网络结构简单、学习速度快等优点，被广泛应用于非线性复杂对象的建模[5]。本文将以排气消声器的拉深成形过程为例，研究有限元模拟和神经网络相结合进行压边力曲线优化的方法。

1 基于CAE仿真的神经网络压边力优化

建立的RBF网络模型要能实现预测，必须先对网络进行训练，这就需要大量的样本。我们采用数值仿真的方法获得训练和测试样本。

1.1 有限元模型的建立

采用有限元仿真软件Dynaform模拟排气消声器的拉深成形过程，材料采用SPCE，料厚2.0mm，材料性能参数为：弹性模量E=202GPa,屈服点σs＝203MPa,泊松比µ＝0.28，抗拉强度σb＝ 425MPa,材料密度 ρ ＝ 7.85×103kg/m3，硬化指数n＝0.2，各向异性指数r＝2.0。CAE模型如图1所示。

1.2 RBF神经网络的建立

1.2.1 确定网络结构

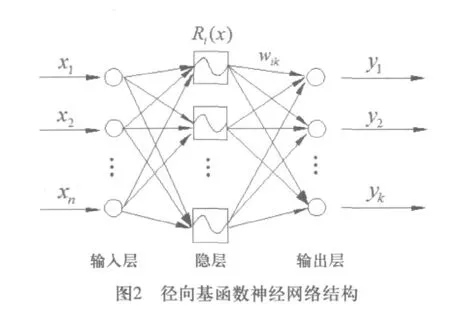
RBF神经网络是一种具有单隐层的前向神经网络。一个典型的RBF网络包括三层：输入层、隐含层和输出层，其网络结构如图2所示。输入层节点只传递输入信号到隐层；隐层节点由像高斯函数那样的辐射状传递函数构成，而输出层节点通常是简单的线性函数。

隐含层采用高斯函数作为基函数，其表达式如下：消声器实际压边圈面积为3.7×105mm2，数值模拟试验时取压边力变化范围为(1～3)×103kN。在保持其他工艺参数不变的情况下，如图3所示的6种典型变压边力加载模式进行数值模拟，获得神经网络样本，归一化后的训练样本如表1所示。

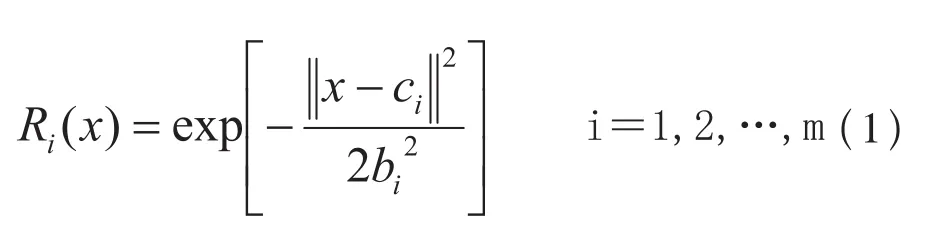
式中：x—n维输入矢量；ci—第i个基函数的中心；bi—基函数宽度；m一隐层节点个数。

从图2可以看出，输入层实现从x→Ri(x)的非线性映射，输出层实现从Ri(x)→yk的线性映射，即

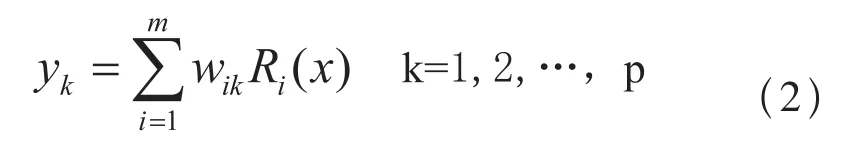
式中：p一输出节点数；wik—权值。

在利用RBF神经网络逼近非线性映射时，通常采用最小二乘法对网络进行训练。输入变量x＝[x1x2x3]，输出变量y＝[y1y2y3y4y5]。

其中：x1—最大等效应力；x2—最大等效应变；x3—板料最大减薄率。

y1～y5——凸模行程5个不同位置对应的压边力。

1.2.2 确定训练样本

采用变压边力进行拉深成形时，为避免零件出现起皱或破裂，通常将压边力限制在一定的区间内。压边力F＝Aq，其中A为压边圈面积，q为单位压边力。查冲压手册取q＝3.9MPa ，排气

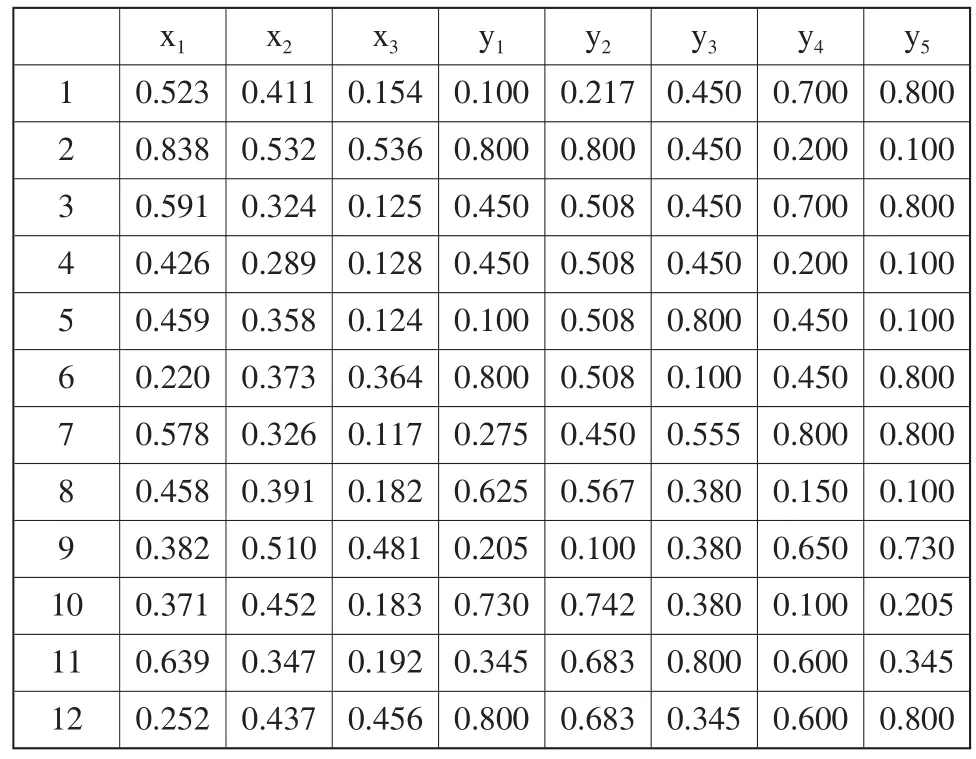
表1 归一化的训练样本

1.2.3 训练的结果及网络的验证

通过多次实验，获得最佳基宽度参数b＝0.79。从图4中可以看到，在网络训练过程中，误差随训练次数增加而逐渐减小。网络经过146次迭代运算后，网络的拟合误差降到了10-4以下，达到设定误差，网络停止训练。最终确定RBF网络模型的结构为：3—146—5。取检验样本对网络性能进行检测，表2显示了部分样本的检验结果，从表中可看出网络的计算是可靠的。

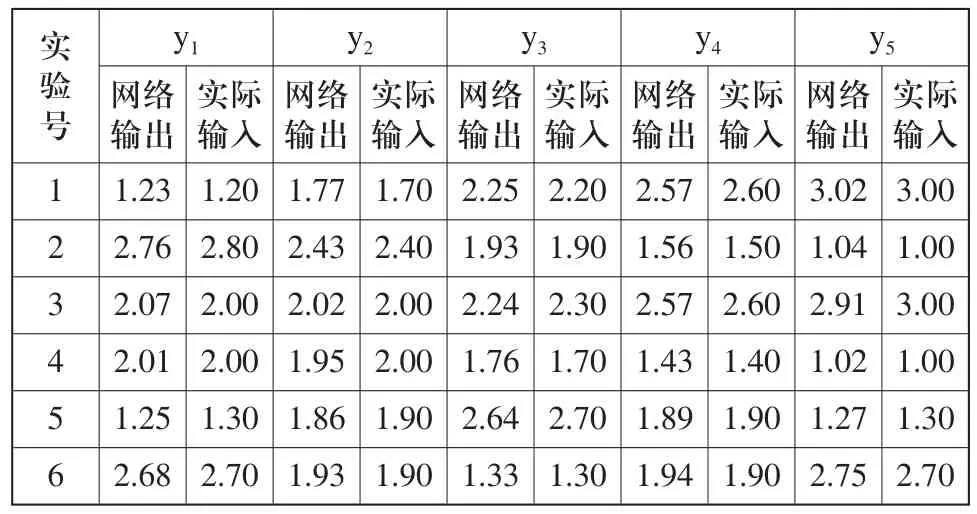
表2 网络检验

2 结论

本文将有限元与神经网络相结合，用于变压边力的优化设计，建立变压边力优化的神经网络模型，训练好的神经网络可实现压边力的优化设计，对实际设计起到指导作用。同时，借助CAE仿真计算，将通常复杂的神经网络输入参数综合为三个影响因素，即最大等效应力、最大等效应变和板料最大减薄率，具有极大的实用性。

图7 成形效果图

[1] 谢晖, 钟志华.基于CAE和神经网络的压边力优化[J].机械工程学报, 2004, 40(7): 105-109.

[2] Mattiasson Kjell, Bernspang Lars.On the use of variable blank holder force in sheet metal stamping.Simulation of Materials Processing:Theory, Methods and Applications,1998.

[3] 包友霞, 徐伟力, 刘罡, 等,薄板成形中变压边力优化设计方法[J].机械工程学报, 2001, 37(2): 105-109.

[4] 高裕, 朱伟, 董湘怀.变压边力对复杂零件成形性能的影响[J].塑性工程学报, 2006, 13(5): 87-91.

[5] 黄玉萍, 阮锋, 蔡志兴, 应用神经网络优化压边力[J].模具工业, 2008,34(7): 9-12.