复杂情况下大规模船队规划模型与求解方法＊

杨秋平 谢新连 裴光石

（交通运输部水运科学研究院1） 北京 100088） （大连海事大学交通运输管理学院2） 大连 116026）

船队规划是航运企业发展战略中的一项重要决策，是决定企业能否长期生存发展的关键问题.通过对船队规划及相关文献的查阅分析发现［1－6］，目前传统船队规划方法对于解决变量较少、约束条件较少且变量之间呈线性关系的船队规划研究和应用比较成熟［7］，但对于多航线、多型船、大规模的船队规划问题研究仍不是很理想.因此，船队规划的研究工作需要进一步改进和完善.本文针对船队规划问题规模大、影响因素复杂、要求整数解等一系列特点，提出了复杂情况下大规模船队规划模型与求解算法，为解决这类实际问题提供了一种新方法.

1 船队规划数学模型

1.1 问题描述

针对一个拥有多种类型船舶的大型船队，以船队在某一时刻的状态为起点，根据未来一段时间的航运市场行情预测研究在复杂市场环境下考虑船舶营运经济状态、企业投资能力、多种类型投资方式等影响因素，如何逐步调整船队的规模与结构，在适当时机购置船舶、租赁船舶、更新船舶，适应港口、航道、货流新变化的需要，保持足够的运输能力和竞争力.通过建立船队规划数学模型，解决大型船队在不同时期添置什么类型船舶、添置多少、租赁什么类型船舶、租赁多少、出售什么类型船舶、出售多少以及如何运用船舶等动态规划问题.

1.2 船队规划模型

1）基本假设 （1）船队承担运输任务的网络是由若干装货港和若干卸货港组成，通常船舶都能在装货港一次装满货物出发，航行到卸货港，一次全部卸空货物，然后空载返回装货港再准备装货；（2）研究期（规划期）为N，单位为a，为资金结算的一个时间单位；（3）已对各航线上的货物运输需求做出预测；（4）在研究期内共有K种船型可供选择；（5）船舶买卖、租赁发生在年初，退租发生在年末；（6）考虑到造船周期内的预付资金利息或买船代理费等因素，令船舶买入价格比售价高一百分比α；（7）考虑到船舶租出时船东应支付给经纪人佣金，令佣金等于所付租金乘以租约规定的百分比μ；（8）租船业务采用期租船形式，租期最少为1a，最长为整个研究期；（9）每年营运支出与买船、租赁船支出均发生在年初，不考虑研究期前的投资费用.

2）变量与参数定义 决策变量xjbht，第t年在h航线上配置的b年建造的j型船的数量；yjbht，第t年在h航线上配置的b年建造的j型船的年航次数；ojbt，第t年闲置b年建造的j型船的数量；sjbt，第t年购买b年建造的j型船的数量；wjbt，第t年出售b年建造的j型船的数量；ujbdt，第t年租入b年建造的j型船的数量，租期为d年；vjbdt，第t年租出b年建造的j型船的数量，租期为d年.

参数Rjbht，在第t年时b年建造的j型船在h航线上营运的平均航次毛收益；Pjbdt，第t年租赁租期为d年的b年建造的j型船的租金；Ejbt，在第t年时b年建造的j型船的售价；Fjbt，在第t年时b年建造的j型船的年度闲置费用；Ajb，在研究期之初船队中拥有的b年建造的j型船的数量；Wjb，b年建造的j型船在研究期末的回收价值；θjht，第t年j型船在h航线上的装载率；Dj，j型船的额定装载量；WTht，第t年h航线上的最大货物运输需求量；tjh，j型船在h航线上的单航次往返时间；Tj，j型船的年可营运时间；Qjbt，在研究期之初拥有的需于第t年末退租的b年建造的j型租赁船的数量；Mt，第t年船舶融资限额；Njbt，第t年市场上可供租赁的b年建造的j型船的数量；B0，在研究期之初船队中拥有的最老船舶的建造时间（B0≤0）；i0，考虑资金时间价值的折现率；α，买船代理费占售价的百分比；μ，船舶租出的佣金占租金的百分比；β，对研究期末船队实物价值的重视程度系数（0≤β≤1）；K，船型总数；G，航线总数；N，研究期年数；NT，船舶的寿命期；Rt，第t年营运的航线集合；Φht，第t年可在航线h上营运的船型集合.

3）数学模型 针对上述问题，以追求研究期内船队现金流量的折现值最大为目标函数，建立船队规划数学模型（P1）如下.

目标函数：

约束条件：

其中，式（1）为目标函数，它等于各年度收入的现值减去各年度支出的现值加上研究期末剩余回收部分的现值；式（2）为营运时间约束；式（3）为载货能力上限约束；式（4）为船舶数量约束；式（5）为船舶融资约束；式（6）为船舶租入数量约束；式（7）为船舶出售与租出数量约束；式（8）为新船出售数量约束；式（9）为新船租出数量约束；式（10）为船龄约束；式（11）为航线与船型相容性约束；式（12）～（13）为变量约束.

2 求解方法

该模型是一个大规模混合整数船队规划模型.模型涉及到的变量和约束条件较复杂，当问题规模较大、航线数、船型数较多的复杂情况下，将很难在短时间内求得全局最优解.为了提高优化计算的收敛性且不破坏所求解的精度，采用Benders分解算法来求解大规模船队规划问题，将非常复杂的优化问题分解为较为简单的问题来处理［8－10］.Benders分解算法的计算步骤如下.

步骤1初始化参数.设原问题的上、下界分别为：UB＝ ＋∞，LB＝－∞；上下界的容许误差为ε＝10－5；设定迭代计数变量m＝0，最大迭代次数为M＝105.

步骤2利用分枝定界算法求解原问题的松弛主问题（MEP1），若此问题有最优解，将求出的目标函数值ZU作为新的上界UB，令UB＝min｛ZU，UB｝，并将求解出的变量值固定，代入子问题对应的对偶问题中，转向步骤3；若此问题为无界解，则任选一组可行解，转向步骤3；若此问题无解则算法停止，原问题无解.

步骤3对子问题对应的对偶问题进行求解，其求解的结果将会有两种情况：无界或存在最优解.若所求对偶问题无界，应对松弛的主问题增加约束条件即添加割平面去掉不可行解，令m＝m＋1，转向步骤1；否则转向步骤4.

步骤4若所有的对偶子问题都可求得最优解，将其对偶解记为＾Uht，＾Vjt，＾Cjht目标函数记为

令LB＝max｛ZL，LB｝，转向步骤5.

步骤5检验收敛性，若UB－LB＜ε或m＞M，算法停止；否则，令m＝m＋1，对主问题添加割平面：

然后转向步骤1.

3 实例分析

以我国某大型航运企业原油运输船队为例，该公司计划未来每年投入1.5亿美元用于船队的建设.规划期初船队的详细资料如表1所列，各型船的年最大营运时间为345d，寿命期限为20a，由于水深限制，VLCC型油轮不适于在东南亚航线航行.为提高船队的整体技术性能，规定每年购置船舶的船龄不超过5a；考虑到租船市场的实际情况，假设市场上每年每型船的租赁上限为10艘.通过预测得到各年各航线的运输需求量如表2所列，由于篇幅有限，其他数据未列出.计算参数值如下：i0＝8%，α＝3%，μ＝1.25%，β＝1.

根据以上给出的计算参数，利用Benders分解算法对该公司的大型船队规划问题进行求解，得到优化结果如下：规划期内船队现金流量的折现值为378 789.39万美元.各年度船舶购置和租入方案见表3，各年度船舶租出方案见表4.各年度船舶调配方案见表5.

表1 研究期前船队构成

表2 各年各航线的运输需求量 万t

表3 船舶购置和租入优化方案

表4 船舶租出优化方案

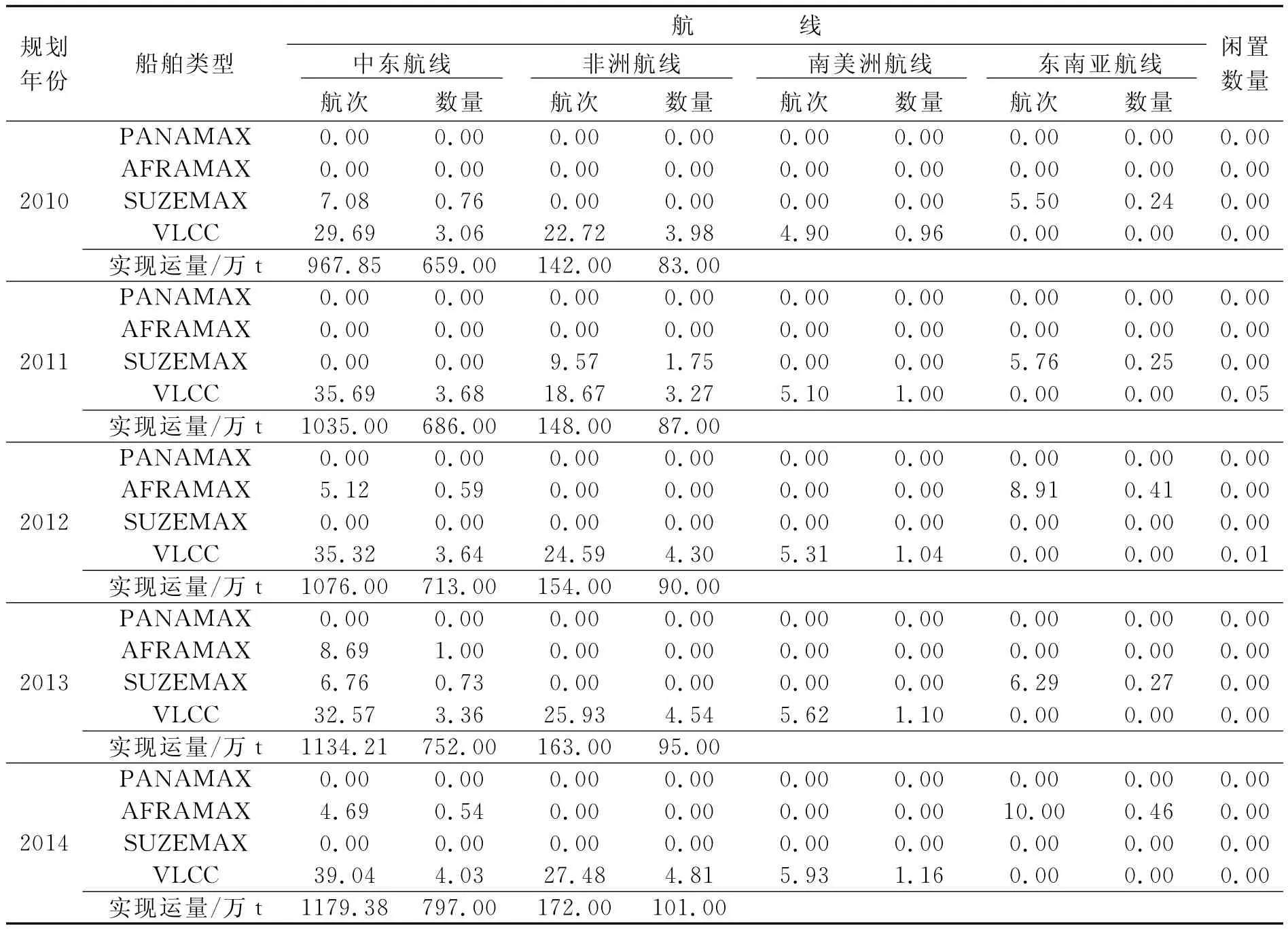
表5 船舶调配优化方案

从上述优化方案可知，该公司的油轮船队运力相对于未来5a各航线上的原油进口量来说是充足的.为了充分使用船舶资源、降低闲置成本、提高经济效益，将自有船舶租出也是公司采用的主要经营策略之一.从船队运力的配置上看，由于原油进口航线大多数为远洋航线，多倾向于采用大型船舶，以VLCC型油轮为运输主力，其他船型的油轮作为补充.

4 结束语

本文针对复杂情况下在多航线上、由多种类型船舶构成的大型船队规划问题进行了研究.在综合考虑订造新船、买卖二手船和租赁船舶等多种可能存在的实际情况，以及船舶营运经济状态、企业投资能力等影响因素的基础上，建立了船队规划混合整数规划模型.以我国某大型航运企业原油运输船队作为研究的基础原型进行实证分析，验证所提出的模型及算法对于大规模实际问题的应用效果.结果表明，该方法实现了多航线、多型船、大规模混合整数船队规划问题的优化求解，可为大型航运企业进行船队规划决策提供支持.

［1］Christiansen M，Fagerholt K，Ronen D.Ship routing and scheduling：status and perspectives［J］.Transportation Science，2004，38（1）：1－18.

［2］Christiansen M.Maritime Transportation.Handbook in OR ＆ MS，2007，14（6）：189－284.

［3］杨秋平，谢新连，赵家保.船队规划研究现状与动态［J］.交通运输工程学报，2010，10（4）：85－90.

［4］谢新连，李树范，纪卓尚.船队规划的线性模型研究与应用［J］.中国造船，1989（3）：59－66.

［5］Xie X，Ji Z，Yang Y.Nonlinear programming for fleet planning［J］.International Shipbuilding Progress，1993，421：93－103.

［6］Cho S C，Perakis A N.Optimal liner fleet routeing strategies.Maritime Policy and Management［J］，1996，23（3）：249－259.

［7］杨秋平，谢新连.多种类型投资的船队规划模型［J］.上海海事大学学报，2010，31（1）：61－66.

［8］黄红选，韩继业.数学规划［M］.北京：清华大学出版社，2006.

［9］邴凤山，刘振宏.一种数学规划的分解算法（续篇）［J］.水电能源科学，1998，16（2）：43－48.

［10］杨秋平.船队规划数学建模及算法研究［D］.大连：大连海事大学交通运输管理学院，2010.