基于频率的大素数高效生成算法

2011-07-05汤鹏志

华东交通大学学报 2011年5期

汤鹏志，李彪

（华东交通大学基础科学学院，江西南昌330013）

1977年Ron Rivest、Adi Shamirh和Len Adleman提出公钥密码体制（RSA）加解密算法，其安全性在于在计算机上生成两个足够长度的大素数，其乘积具难分解性[1-2]。目前，素数确定性算法主要分为递归试除法，Eratosthenes筛法，Miller检验和多项式时间内判定的素数（AKS）算法。文献[3]分析表明，Eratosthenes筛法是一种较好的素数确定性算法。根据文献[4]，任意素数（除2和3）均可表示为的理论，可提升筛法效率。生成大素数的方法是随机产生一个大整数，然后进行素性检测。文献[5]提出一种用概率方法来研究素数的分布，是提升大整数素性的有效途径。常用的素数检验算法主要为Fermart算法、Solovay-Strassen检测法、Lehman检测法、Miller检验、Miller-Rabin检测法和AKS算法[6]。通过分析当今的大素数生成方法与原理[7-11]，提升大整数的素性和选择优良的素数检验算法，从而提出一种改进的大素数的高效生成算法。

1 构建素数库

对素数的分布频率研究，需建立在素数库的基础之上。在素数的研究领域中，确定性素数算法存在很多，如试除法，Eratosthenes筛选法，Miller检验，AKS算法等。在素数算法中，Eratosthenes筛法应用非常广泛。传统Eratosthenes筛法需要对每个数依次比较，算法的效率较为低下，通过对Eratosthenes筛法进行优化，得出素数库构建算法。

定理1 除2和3之外，素数均可表示成6k±1(k∈N)的形式。

定理2 如果k为素数，则k×j(j∈N+)必为合数。

推论1 在Eratosthenes筛法中对寻求到的第一个素数k，在区间(1 ，k2)没有被划掉的数均为素数。

定义一个bool型素数判定数组p[n+1]。根据定理1，当i=2或i=3或i=6k+1或时，p[i]=true；否则p[i]=false。寻找第一个p[i]=true(i∶ 5↦n)的素数i，i的倍数均为合数。另外，数组赋值时已去除偶数，将内层循环j限定为奇数。故当素数为时，有。最后所有满足的i就是区间的所有素数。算法如下

2 素数的频率分布

素数具有无穷多个，并且随区间变大而逐渐变得稀疏。通过运行素数库构建算法，得到区间(0 ，109)中的素数库，从而考察素数的尾数分布情况。

定义1 在某个区间范围内，用素数模100的余数进行分类，各类余数中拥有素数的个数称为素模百频数。

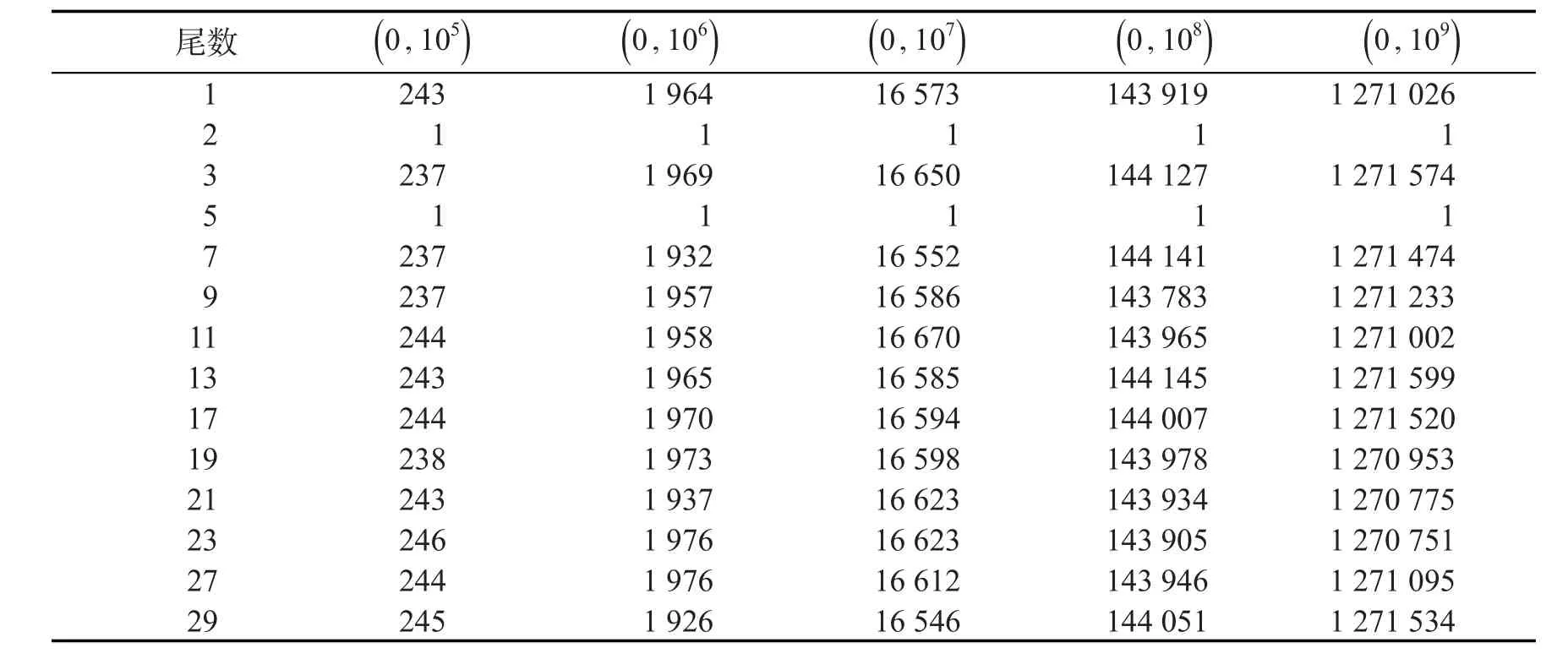
表1 各区间的素模百频数Tab.1 Frequency of module in various regions

通过表1可知，素数尾数的分布大致相同，即任何尾数在区间中所占的素数的概率是同等的。如若一个整数在生成之时，已经排除存在部分素因子，则它是素数的可能性会更大。

定义2 在某个区间范围内，满足表达式ΠPi×k+1（Pi为小素数）的整数中，所占素数的个数称为素积频数。

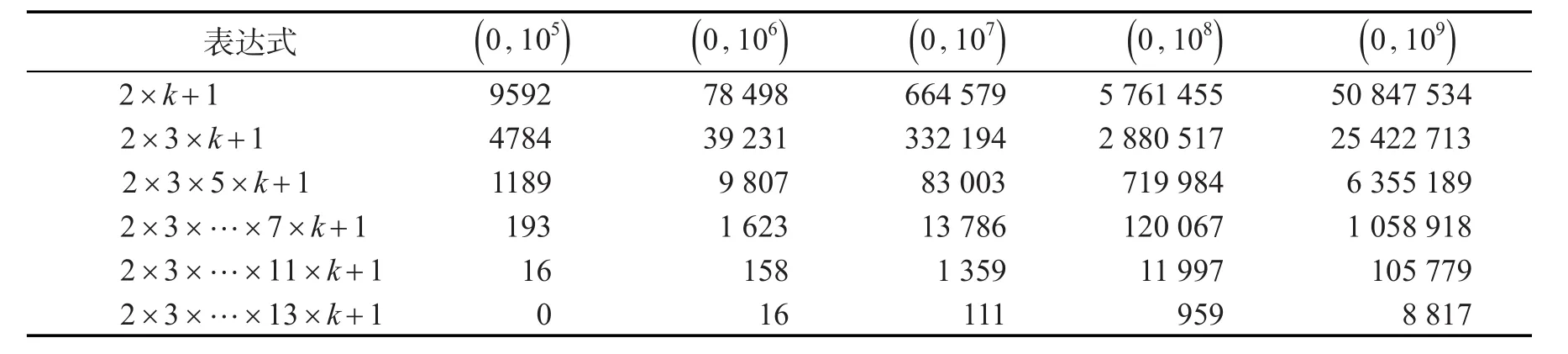
表2 各区间的素积频数Tab.2 Frequency of prime number in various regions

通过观察表2中的数据，随着过滤的素因子的个数增加，区间内的素积频数逐渐减少。但随着表达式过滤素因子的个数增加，无法清晰得到该表达式下整数是素数的可能性变化状况。

定义3 在某个区间中，满足表达式ΠPi×k+1（Pi为小素数）的素积频数与整数个数比值，称为素积频率。

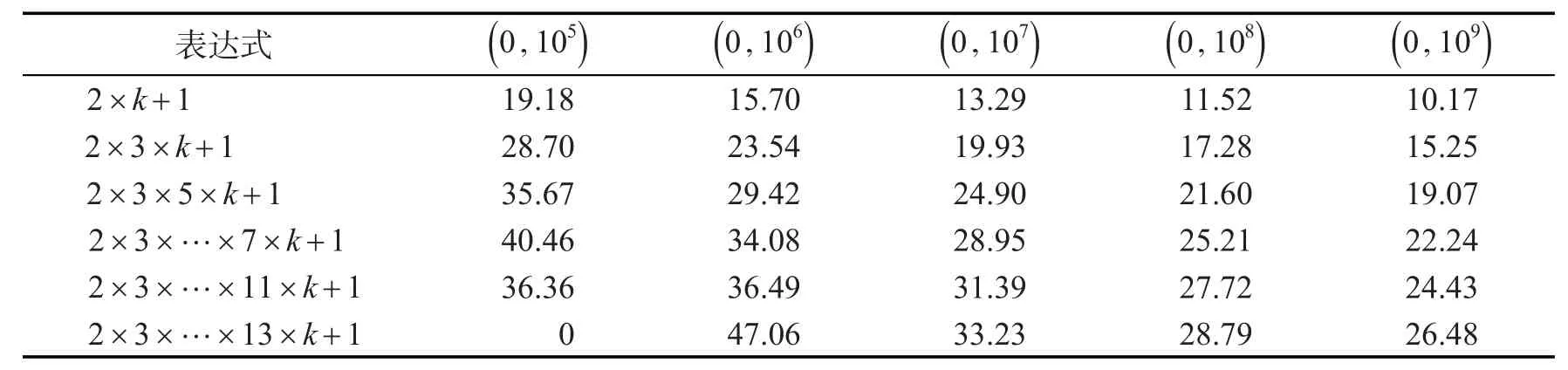
表3 各区间的素积频率Tab.3 Frequency of prime number in various regions %

通过分析表3中的数据，随着过滤的素因子的个数增加，区间内的素积频率逐渐增大。通过实践表明:采用小于512的素数可以淘汰大约82%的非素整数。

3 素数检验算法分析

素数检验算法分为确定性检验算法和概率检验算法。通过确定性检验算法的得到的数一定是素数，Miller检验和AKS算法就是常用的确定性算方法。通过概率性检验算法得到的数只是伪素数，Fermart算法、Solovay-Strassen检测法、Lehman检测法和Miller-Rabin检测法是现今流行的概率算法。确定性检验算法需要深厚的数学理论基础，算法的实现相当复杂。而概率检验算法虽然存在一定的概率得到伪素数，但经过多次测试可将报错率控制在极低的范围内。通过表4的算法分析，可知Miller-Rabin算法是素数检验算法中的最佳选择。

表4 素数检验算法分析情况Tab.4 Analysis of prime number inspection algorithm

4 大素数生成算法

通过改进ISO/IEC标准[12]，得出一种高效的大素数生成算法。在实际的工程中，如若需要生成一个1 024位（二进制数）的素数q，则必须满足，其中。依据分析，满足表达式2×3×5×…×509k+1(k∈N)的整数已经滤掉了所有小于512的素因子，该数在生成时就已经过滤掉80%以上的非素数。在素数的生成和检验算法实施前，需要计算参数m，n，kj，其中1≤j≤97且j∈N，m=2k1×3k2×5k3×…×503k96×509k97，n=2×3×5×…×503×509，并且m必须满足m+1≥qmin。在算法中，每迭代一次整数q需要加n，其中q=q+n，保证筛选的范围内的整数的个数，必须对n的数量级进行分析。由于n=2×3×5×…×503×509＜21×22×23×…×210×210=2746，则在筛选的范围中存在的整数个数i=21023/2746=2277个。在如此大的区间中，一定能够找到若干个素数。算法如下

5 结论分析

本文提出了一种对素数尾数的分类频数和表达式下素数频率的分析方法，通过小素数对整数进行初次过滤，经过对素数检验算法的全面剖析，最后使用Miller-Rabin算法对形如ΠPim×n+1（Pi为小素数）的整数进行检验。算法中通过利用1 024位和746位的两个大整数空间存储中间数据，跳跃大整数含有小素数因子的可能，降低算法的循环遍历次数，从而提升了算法的运行效率。

表5数据表明，本文的大素数生成算法可以快速的生成若干个大素数，从而为RSA加解密算法提供强有力的安全保障。