经济增长与工业废水排放量实证分析
2011-07-04李少红
□文/李少红
一、引言
改革开放以来,中国的经济增长带来了人民生活水平的提高以及社会福利水平的改善,但随之而来的是一系列环境问题。经济增长与环境恶化之间的两难冲突备受关注,二者关系的研究已成为各领域探讨的热点问题。经济学家库兹涅茨1955年提出了著名的倒U型曲线假说,20世纪九十年代,Grossman和Krueger在库兹茨曲线基础上提出了环境库兹涅茨曲线。国内学者方行明、刘天伦通过建立一个一元三次的计量经济模型,应用最小二乘法估计,认为工业废水排放量与人均GDP之间存在倒N型的关系,彭水军、包群通过广义的脉冲分析,认为人均GDP与工业废水排放量存在N型关系。而本文主要利用VAR模型来分析经济增长与工业废水排放量是否存在上述关系,首先建立工业废水排放量和经济增长这两个指标,因为考虑到时间序列的平稳性问题,要利用单位根检验数据是否平稳。如果数据平稳或是协整,则建立经济增长与工业废水排放量的VAR模型,进行格兰杰因果关系分析和脉冲响应分析。
二、变量选取与数据处理
(一)变量选取。因为本文只是单纯地研究经济增长与工业排放量之间的关系,不考虑对环境造成污染的其他因素的影响,所以在变量选取方面比较容易。经济增长的指标选用人均GDP(单位:元),之所以选用该指标,在于与总收入相比,人均GDP更能反映出真实收入水平变化对环境的影响。而工业废水排放量的指标就直接选用每亿元工业产值的工业废水排放量(单位:吨)。研究区间取自1995~2009年,各指标数据来源于《中国统计年鉴》。
(二)数据处理。为避免数据的剧烈波动,消除可能存在的异方差,考虑到对时间序列进行对数化处理后容易得到平稳序列,且并不改变序列数据的特征。本文分别对每亿元工业产值的工业废水排放量和人均GDP的时间序列数据进行取对数的处理,新的序列分别命名为lnmyczw和lngdp。
(三)变量的平稳性检验。为了得到有效的检验统计量,防止为回归的产生,在建立VAR模型前应首先对变量的时间序列数据进行ADF平稳性检验。
在进行ADF单位根检验之前,首先应确定是否具有截距和时间趋势项,否则,检验的结果将会大相径庭。一般采用图形观察法,如果序列在偏离0位置变动,且呈现出随着时间快速递增或递减的趋势,则可以选择既有截距又有时间趋势项;如果序列随时间递增或递减的并不迅速,可以考虑舍去时间趋势项。从表1中我们可以看出,lngddp和lnmyczw这2个时间序列在10%的显著性水平下均不能拒绝存在单位根的原假设,因此都是非平稳的。而他们的一阶差分序列dlngdp和dlnmyczw的ADF值均可以小于10%的显著性水平下的临界值,所以都是平稳的。因此,dlngdp和dlnmyczw都是平稳的时间序列,可以建立任何的模型。(表1)
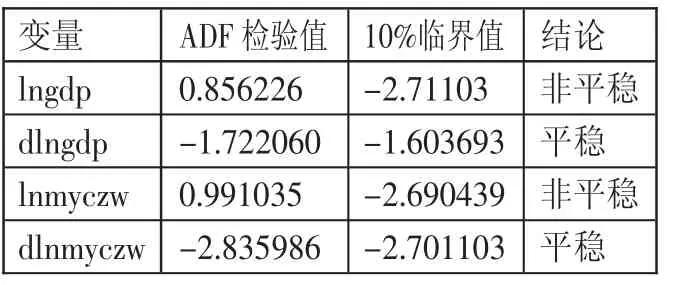
表1 ADF平稳性检验
三、VAR模型的建立及应用
(一)建立VAR模型。在ADF检验的基础上,我们建立人均GDP和每亿元工业产值的工业废水排放量为因变量,这些变量的滞后项为自变量的VAR模型。
为了确定VAR模型的滞后阶数,我们根据 LogL、LR、FPE、IC、SC 和 HQ 等标准进行确定,如表2所示。(表2)滞后阶数适当加大,可以消除误差项中的自相关,但又容易减少自由度,影响模型参数估计的有效性。因此,我们重点参考AIC和SC最小的评价标准,将VAR的滞后阶数确定为4阶。因为对于变量人均GDP和每亿元工业产值的工业废水排放量,经过取对数和一次差分后,变量是平稳的,所以可以建立滞后4阶的VAR模型。

表2 VAR模型的最优滞后期

表3 格兰杰因果检验
(二)格兰杰因果关系分析。在建立VAR模型的基础上,来分析经济增长与工业废水排放量之间的格兰杰因果关系。Granger因果检验度量的是:对y进行预测时x的前期信息对均方误差MSE的减少是否有贡献,并以此作为因果关系的判断基准。与x的前期信息相比,若MSE无变化,则称x在Granger意义下对y无因果关系;反之,当x的前期信息对MSE的减少有贡献时,称x在Granger意义下对y有因果关系。即一个变量如果受到其他变量的滞后影响,则称它们具有Granger因果关系。
Granger因果检验往往受滞后长度p的影响。处理滞后期有两种方法:一是从滞后1开始测试,按AIC、SC最小的原则确定VAR的滞后长度,作为Granger因果关系检验的滞后期;二是尝试不同的滞后期,比如滞后1~6期,观测因果关系的变化特征。本文的滞后阶数直接利用VAR模型所确定的滞后阶数。
通过格兰杰因果关系检验(表3),根据伴随概率,在5%的显著水平下,因为0.000,0.05,所以拒绝原假设,即人均GDP是工业废水排放量的格兰杰原因。0.9569>0.05,所以接受原假设,即工业废水排放量不是人均GDP的格兰杰原因。表明人均GDP和工业废水排放量之间存在单向的格兰杰因果关系。这就从一个方面反映了我国经济的快速增长在一定程度上建立在高废水排放量的基础上的,但是这不符合中国的“低污染,高增长”的目标,所以我国要加快经济增长由粗放式向集约式的转变,治理高能耗、高排放的企业,而且在较快的经济增长的条件下,也应该对工业废水的治理增加投资。
(三)脉冲响应分析。前面我们分析了一个变量和另一个变量之间的格兰杰因果关系,接下来分析当一个误差项发生变化即模型受到某种冲击时对系统的动态影响,或者说VAR模型中的一个内生变量的冲击(即一个误差项发生变化)给其他内生变量带来的影响,即脉冲响应分析。首先,我们给每亿元工业产值的工业废水排放量一个单位的冲击,采用脉冲方法得到关于人均GDP的一个脉冲响应函数(图1)。图1中,横轴表示冲击作用的滞后期间数(单位:年),纵轴代表人均GDP增长率的响应,实线表示脉冲响应函数,代表人均GDP的增长率对每亿元工业产值的工业废水排放量的冲击的反应,虚线表示正负两倍标准差的偏离带。
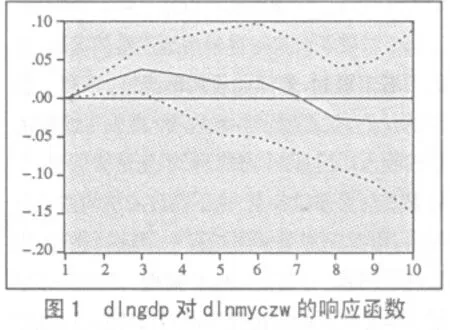
从图1中可以看出,当在本期给人均废水排放量一个正冲击,人均GDP的增长率在前7期基本上是平稳的,且是正的,当人均废水排放量受外部的某一正的冲击后,传递给人均GDP的增长率,给人均GDP的增长率带来同样的冲击即具有正的增长。在第7期内下降为0,并持续下降,到第8期以后开始稳定(响应值为-0.03)。表明每亿元工业产值的工业废水排放量的正的冲击可以使人均GDP的增长率持续降低,但是这种影响比较微小。
同理,我们给人均GDP一个单位的正的冲击,可以得到每亿元工业产值的工业废水排放量的响应函数(图2),实线表示每亿元工业产值的工业废水排放量增长率对人均GDP冲击的响应函数。
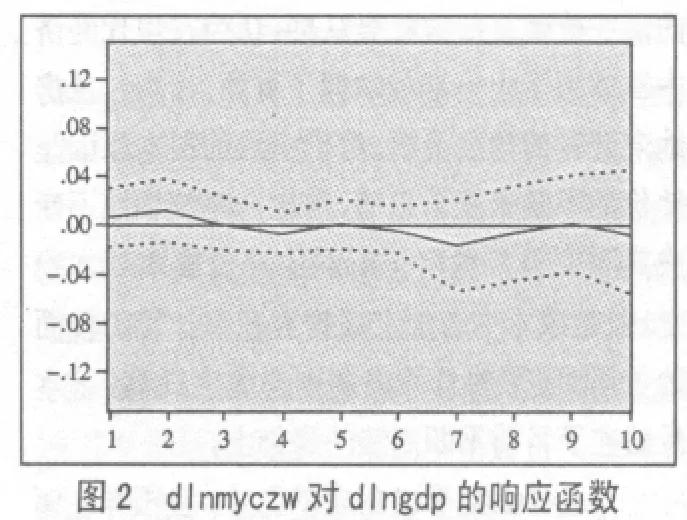
在图2中可以看出,每亿元工业产值的工业废水排放量的增长率一直在0附近很小幅度的波动,但在第3期以后都显示出不明显的负效应。这说明人均GDP的一个正的冲击可以持续降低每亿元工业产值的工业废水排放量的增长率,但是这个响应不是非常明显。
四、结论
在1995~2009年这个研究期间,通过利用人均GDP和每亿元工业产值的工业废水排放量建立VAR模型,通过格兰杰因果关系分析和脉冲响应分析,得出如下结论:
1、在一定程度上,中国经济的增长是工业废水排放量的格兰杰原因,这与中国正处在工业化中期,第二产业比重大的经济结构有关,但是工业废水排放量不是经济增长的格兰杰原因。
2、在响应期内,dlngdp对dlnw的响应函数并没有呈现倒N型或N型。没有呈现倒N型可能是因为使用的模型不同,而没有呈现N型是因为本文数据较新,加上近年来政府对工业废水排放量的控制所致。
3、经济增长对工业废水排放量的减少所起的作用不是很明显。
[1]Grossman G.and Kuerger A:Economic Growth and the Environment[J].Quarterly Journal of Economics,1995.110.2.
[2]夏庆澍,兰天.中国经济增长与环境污染关系的实证性研究 [J].经济观察,2011.1.
[3]方行明,刘天伦.中国经济增长与环境污染关系新探[J].经济学家,2011.2.
[4]彭水军,包群.中国经济发展与环境污染关系[J].中国工业经济,2006.5.
[5]高铁梅.计量经济分析方法与建模[M].2009.5.
[6]吕健.上海市经济增长与环境污染[J].华东经济管理,2010.8.
