内部填充泡沫铝的柱壳力学响应数值模拟*

陈成军，谢若泽，张方举

（中国工程物理研究院总体工程研究所，四川 绵阳 621900）

泡沫铝是一种新型的轻质多孔材料，密度低、比模量和比强度高，具有良好的缓冲吸能特性。泡沫铝填充结构或夹芯结构已被应用于冲击防护、仪器包装等军用和民用领域。随着应用领域的推广，泡沫铝及其组合结构力学响应的分析引起了广泛兴趣。V.S.Deshpande等［1］研究了泡沫铝在单轴与静水压力等载荷作用下的屈服和硬化特性，提出了泡沫金属的几何自相似模型和微分硬化模型，在泡沫材料本构关系的发展中起了至关重要的作用。A.Reyes等［2］验证了多种应力状态下Deshpande自相似模型［1］的有效性，并以密度概率分布的方式初步考察了泡沫铝内部胞孔不均匀性对力学性能的影响。郭伟国等［3］利用实验方法研究了应变率和密度对泡沫铝力学性能的影响，分析了不同应变率下泡沫铝的变形与破坏机理。S.P.Santosa等［4］对准静态轴向压缩载荷作用下的泡沫铝填充薄壁方管的屈曲变形进行了大量的实验研究和数值模拟，在此基础上提出了泡沫铝填充方管平均压缩载荷的理论公式。S.Shahbeyk等［5］研究了泡沫铝的自相似本构模型，并数值模拟了轴向冲击载荷作用下内部填充泡沫铝方管的动态变形。赵桂平等［6］数值模拟分析了不同厚度的泡沫铝合金夹层板在冲击载荷下的动态响应，并讨论了其变形机制。由此可见，泡沫金属及其组合结构力学特性的研究已成为一个学术热点问题。

然而，由于泡沫金属几何拓扑与力学特性的复杂性，泡沫金属及其组合结构力学响应的理论与数值方法研究还不完善，有必要深入研究。对于内部填充泡沫铝的圆柱壳的力学响应问题，由于圆柱壳的屈曲变形以及壳体与泡沫铝芯材的耦合作用，数值模拟分析非常困难。本文中，在泡沫铝组合结构模型实验的基础上，尝试利用唯象本构模型描述泡沫铝材料的宏观力学行为，采用有限元法模拟内部填充泡沫铝的圆柱壳的整体静、动态响应，拟为下一步泡沫铝填充柱壳的吸能分析提供数值方法上的支持。

1 模型实验

泡沫铝的基体材料为铝铜合金ZL201，采用熔体发泡法制备成闭孔泡沫铝，名义空隙率为85%，表观密度为0.38～0.41 g/cm3，孔径为2～3 mm。利用线切割加工成∅94 mm×88 mm的圆柱型芯体。圆柱壳试件的外形尺寸为∅96 mm×87 mm，壁厚1 mm，材料为A3钢。泡沫铝组合试件（即内部填充泡沫铝的圆柱壳）由外部的圆柱壳和泡沫铝芯体构成，泡沫铝芯与外壳用胶粘接。

对圆柱壳及组合试件进行了准静态、动态轴向压缩实验。准静态压缩实验在Instron1196材料试验机上进行，以5 mm/min的变形率进行单轴加载，记录实验过程中的力-位移曲线。动态轴向压缩实验DHR9602型落锤试验机上进行，通过落锤装置上的冲击加速度计测定撞击过程中锤体的加速度变化获得试件加载端的作用力;利用200XH光电引伸仪全程监控撞击过程，获取试件变形的位移信号。在落锤实验中，由于加速度计采集的信号幅值很小，且高频干扰严重，很难分离出有效信号，所以未能获得加载过程中的力-位移曲线。

2 数值模拟

2.1 材料模型

由于泡沫金属中胞孔的存在，泡沫金属的力学特性与致密金属材料有很大的不同，其力学响应具有2个典型特征［1，5］，即静水压力影响屈服和体积塑性可压。对于前者，将应力第一不变量包含在屈服函数的定义中即可;对于后者，引入非关联塑性流动模型是常用的处理方式。Bilkhu/Dubois可压缩泡沫模型［7］正是采用了这种方法，该模型为各向同性硬化模型，其屈服函数定义为

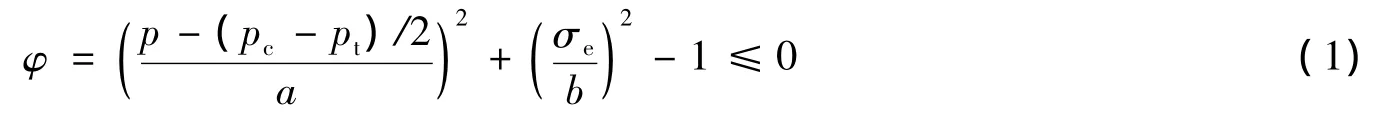
式中:p为静水压力，材料的压缩屈服强度pc为体积应变εV的函数

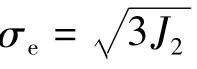
而b是将单轴压缩实验数据带入式（1）计算得到的

这里材料单轴压缩流动应力σy描述为单轴应变εα的函数

材料的塑性流动采用非关联塑性模型描述

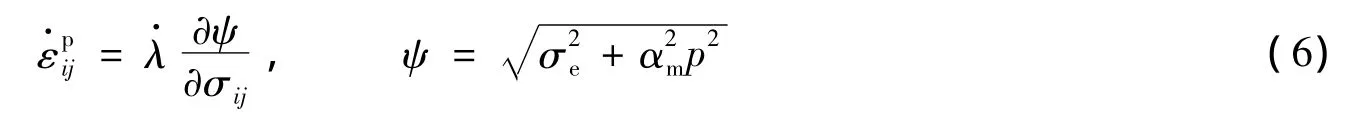
图1 Bilkhu/Dubois模型的屈服面与加载面Fig.1 The yield surface and loading surface of the Bilkhu/Dubois model

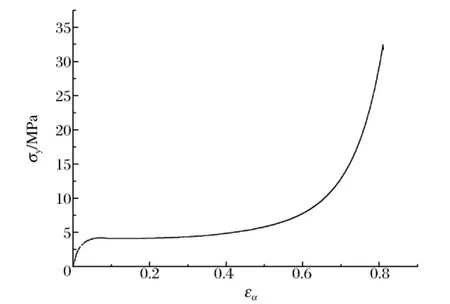
图2 泡沫铝单轴压缩应力应变曲线Fig.2 Uniaxial compression stress-strain curve of aluminum foam

由以上分析可以看出，Bilkhu/Dubois泡沫模型利用了单轴和三轴（静水压缩）数据刻画泡沫材料初始屈服面与加载曲面的演化，可望描述泡沫铝在复杂应力状态下力学响应。计算中，式（5）中的H（εα）是以图2所示曲线确定的数据对（εα，σy）形式输入;式（2）中的Hp（εV）近似采用了H（εα）的数据;塑性泊松比 νp取为0.0;弹性模量取为2.63 GPa。

圆柱壳的A3钢采用运动硬化模型描述

2.2 有限元模型

采用非线性显式积分有限元程序LS-Dyna进行数值模拟，试件的基本构形与有限元网格如图3所示。泡沫铝芯以单点积分六面体单元划分网格;圆柱壳试件以面内单点积分的Belytschko-Tsay四边形壳元进行离散，壳厚度方向采用五点积分以细致描述应力在厚度上的梯度。泡沫铝芯与外壳的粘结作用以“固-连接触”处理，接触载荷满足

图3 试件的有限元网格Fig.3 Element meshes of specimens

时，芯固结在外壳上;随着接触载荷的增大，式（8）的关系被破坏后，芯与外壳之间的作用则处理为一般的面-面接触。式（8）中σ和τ分别为接触面上法向和切向的接触载荷;σf和τf分别表示胶结面所能承受的最大法向、切向载荷。

为与实验状态一致，在试件下端施加刚性墙支承条件，试件上端通过刚块引入载荷条件。在动态实验的数值模拟中，刚块以初始速度的方式施加载荷;在准静态实验的数值模拟中，以下式所示的加载函数在刚块上施加位移

式中:d0为加载刚块的最大位移，即试件总的压缩变形长度;T为载荷总的作用时间。

由于结构的几何缺陷、材料缺陷是不可避免的，而这些因素对柱壳屈曲的影响又非常重要。为简化计算，本文中以预置随机几何缺陷的方式综合考虑圆柱壳可能存在的缺陷形式:初始几何微缺陷以随机扰动的形式引入，即试件的所有有限元节点随机发生1%壁厚的径向位置偏差。

3 数值模拟结果

3.1 圆柱壳屈曲

图4、图5分别为试件静、动态屈曲的最终变形图像。在准静态轴压作用下，柱壳发生塑性渐进屈曲，产生轴对称的变形模式;在轴向冲击载荷作用下，试件产生了非轴对称的金刚石模式。由数值模拟与实验图像的对比可以看出，数值方法不但较准确地模拟了试件的整体变形，而且细致地刻画了试件皱褶的数目、大小等局部细节的变化。

图4 圆柱壳静态压缩下的变形模式Fig.4 Deformation patterns of the cylindrical shell under quasi-static loading

图5 圆柱壳动态加载下的变形模式Fig.5 Deformation patterns of the cylindrical shell under impact loading

图6为圆柱壳静态压缩载荷P-位移d曲线的实验数据与数值分析结果，压缩载荷的峰值对应于屈曲皱褶的形成，峰值间的距离对应于皱褶的长度。由图6可以看出，数值方法得到的载荷-位移曲线与实验数据有很好的一致性。图7为落锤冲击（落锤质量为52 kg，冲击速度为10 m/s）下柱壳的轴向压缩特性曲线。冲击作用下柱壳的平均压缩载荷是静态屈曲平均压缩载荷Pm的1.48倍，这与下式理论预测［8］的1.3倍相差不大

由以上分析可知，本文中针对柱壳静、动态屈曲变形而采用的预置初始几何缺陷的模拟方法以及对准静态过程模拟采用的加载方法是合理的。

图6 柱壳静态压缩载荷-位移曲线Fig.6 Crushing force-displacement curve of the cylindrical shell under quasi-static loading

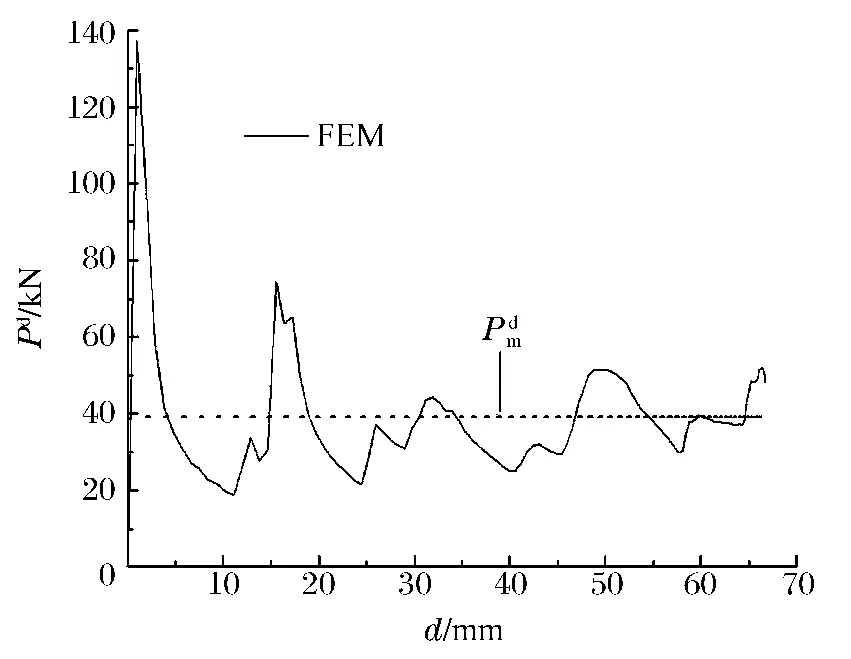
图7 柱壳冲击载荷-位移曲线Fig.7 Crushing force-displacement curve of the cylindrical shell under impact loading

3.2 组合试件

图8为泡沫铝组合试件在准静态压缩加载下的载荷-位移曲线实验数据与数值分析结果。从图中可以看出，第1个屈曲皱褶形成后平均压缩载荷保持为一个相对固定的值，直到第3个皱褶形成，此时泡沫铝芯已被基本压实，然后压缩载荷快速升高。图9为压缩实验结束后试件的最终变形与相应的数值分析结果。由图8～9可以看出，数值分析得到的试件屈曲初始峰值载荷、平均压缩载荷、加载曲线的整体变化趋势，以及试件的变形图像都与实验数据都非常接近，数值方法较好地模拟了准静态压缩下试件的屈曲模态。

图8 准静态压缩加载下泡沫铝填充柱壳的载荷-位移曲线Fig.8 Axial crushing force-displacement curves of the foam-filled shells under quasi-static loading

图9 准静态压缩作用下组合试件的变形Fig.9 Deformation patterns of the foam-filled cylindrical shell under quasi-static loading

图10给出了泡沫铝组合试件落锤实验数值模拟的典型分析结果。表1给出了2种工况下落锤与试件的相互作用时间，以及撞击结束后试件的特征尺寸，表中la，s、la，e分别为试件轴向长度的数值模拟结果和实验结果，dmax，s、dmax，e分别为试件最大直径的数值模拟结果和实验结果，th，s、th，e分别为落锤撞击时间的数值模拟结果和实验结果，工况1为52 kg的落锤以12 m的落高冲击泡沫铝组合试件，工况2为52 kg的落锤以13 m的落高冲击泡沫铝组合试件。由模拟结果可以看出，本文中对泡沫铝组合件在冲击载荷作用下屈曲变形的分析是较准确的。

图10 冲击作用下泡沫铝组合试件的变形Fig.10 Deformation patterns of the foam-filled cylindrical shell under impact loading

表1 试件变形后的特征尺寸及落锤的撞击作用时间Table 1 Characteristic lengths of specimens after deformation and action time of the hammer

4 结论

探讨了内部填充泡沫铝的柱壳静态、动态响应的数值模拟方法，用唯象本构模型描述泡沫金属材料的宏观力学行为，采用有限元方法模拟了泡沫铝结构的整体静、动态响应。基于模型实验的数值模拟结果表明:Bilkhu/Dubois泡沫模型可以唯象地描述泡沫铝在复杂应力状态下的静、动态本构行为;以预置随机几何缺陷的方式处理结构可能存在的缺陷形式用于柱壳的屈曲分析，取得了较好的结果;在准静态实验数值模拟中采用的加载函数形式用于柱壳屈曲分析是可行的。采用的数值模拟方法能够较准确地模拟泡沫铝组合结构在准静态、动态轴向载荷作用下的有限变形弹塑性行为，可以用于泡沫铝组合结构的吸能特性研究。

本文的数值分析中未考虑泡沫铝的应变率敏感性，这是因为实验用泡沫铝在本文中考虑的应变率范围内是率不敏感的［9］。分析中未考虑泡沫材料中胞孔结构和密度分布的不均匀性，这与真实泡沫金属存在一定的差别，而如何在有限元模型中反映这种不均匀性需要进一步深入研究。

［1］ Deshpande V S，Fleck N A.Isotropic constitutive models for metallic foams［J］.Journal of the Mechanics and Physics of Solids，2000，48（6/7）:1253-1283.

［2］ Reyes A，Hopperstad O S，Berstad T，et al.Constitutive modeling of aluminum foam including fracture and statistical variation of density［J］.European Journal of Mechanics:A/Solids，2003，22（6）:815-835.

［3］ 郭伟国，李玉龙，黄福增.不同应变率下泡沫铝的形变和力学性能［J］.爆炸与冲击，2008，28（4）:289-292.

GUO Wei-guo，LI Yu-long，HUANG Fu-zeng.Deformation and mechanical property of aluminum foam at different stain rates［J］.Explosion and Shock Waves，2008，28（4）:289-292.

［4］ Santosa S P，Wierzbicki T，Hanssen A G，et al.Experimental and numerical studies of foam-filled sections［J］.International Journal of Impact Engineering，2000，24（5）:509-534.

［5］ Shahbeyk S，Petrinic N，Vafai A.Numerical modelling of dynamically loaded metal foam-filled square columns［J］.International Journal of Impact Engineering，2007，34（3）:573-586.

［6］ 赵桂平，卢天健.多孔金属夹层板在冲击载荷作用下的动态响应［J］.力学学报，2008，40（2）:194-206.

ZHAO Gui-ping，LU Tian-jian.Dynamic response of cellular metallic sandwich plates under impact loading［J］.Chinese Journal of Theoretical and Applied Mechanics，2008，40（2）:194-206.

［7］ Hanssen A G，Hopperstad O S，Langseth M，et al.Validation of constitutive models applicable to aluminium foams［J］.International Journal of Mechanical Sciences，2002，44（2）:359-406

［8］ Abramowicz W，Jones N.Dynamic axial crushing of circular tubes［J］.International Journal of Impact Engineering，1984，2（3）:263-281.

［9］ 陈成军，谢若泽，张方举，等.Taylor撞击试验在泡沫铝合金力学特性研究中的应用［J］.爆炸与冲击，2008，28（2）:166-171.

CHEN Cheng-jun，XIE Ruo-ze，ZHANG Fang-ju，et al.An application of Taylor impact experiment to study mechanical behavior of an aluminum-alloy foam［J］.Explosion and Shock Waves，2008，28（2）:166-171.