有源电力滤波器的滑模变结构控制
2011-06-20王婷婷
王婷婷
(新疆电力设计院,新疆乌鲁木齐830002)
1 引言
2 有源电力滤波器的数学模型
电力系统中的非线性负荷在大量增加,导致交流电网中的电压和电流波形严重失真。治理谐波、提高电能质量已成为国内外学者研究的热点,对有源电力滤波器APF(Active Power Filter)的研究和应用尤其重视。并联型有源电力滤波器SAPF(Shunt Active Power Filter)是最常用的一种主动型的谐波、无功补偿装置,具有高度可控和快速响应的特性,不仅能对大小和频率都变化的谐波以及无功进行补偿,还可抑制闪变,有一机多能的特点。
由于滑模变结构控制具有强鲁棒性,不受系统模型影响,本文设计了滑模变结构控制器,经过仿真研究,验证滑模变结构控制方法能对SAPF的电流起到有效的跟踪控制作用。
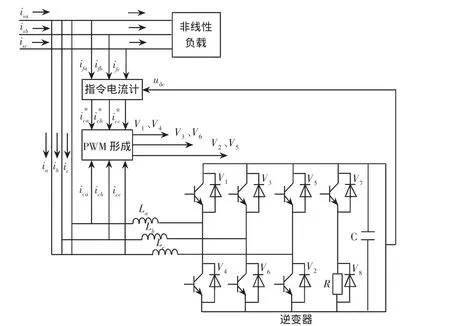
图1 SAPF的原理图
SAPF原理图如图 1所示。ica、icb、icc表示APF实际输出的补偿电流表示APF的指令电流;ifa、ifb、ifc表示负载侧电流;L 表示逆变器输出电感;CT表示电流传感器;C表示为直流侧电容;ja、jb、jc为开关量,控制 6 个开关器件,其中每个桥臂上的开关工作在互补状态。
假设主电路三相电源对称且稳定,开关器件IGBT为理想开关,其控制用开关函数描述,开关函数可定义为:

根据图1所示的电路结构可得到微分方程为:
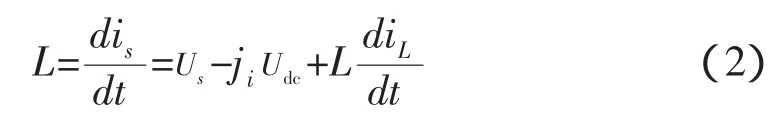
其中:L=(La,Lb,Lc)为 SAPF 的电感;Us=(Ua,Ub,Uc)为电源电压;iL=(iLa,iLb,iLc)。
由于SAPF的作用是通过逆变器输出把电源电流i*s调解成与电源电压Us同相位的正弦波作为控制系统的设计目标。假设电源电压为正弦波,设定电源电流的给定值i*s为:

其中:k为一标量,其大小取决于负载有功功率和SAPF所消耗的有功功率,这将由逆变器直流侧电容电压的闭环控制来调整。
于是,采用SAPF进行电网补偿的问题,转化为如何使电源电流is很好地跟踪参考给定电流i*s。采用滑模变结构控制时可定义状态变量为:
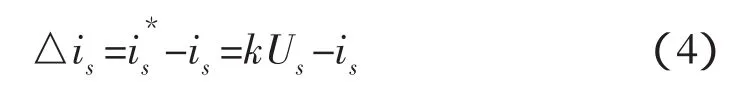
整理式(2)和式(4),可得状态方程
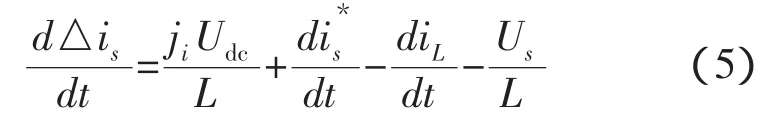
定义

则状态方程(6)可以写为:
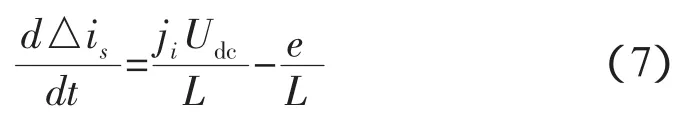
式(7)可以详细写为:
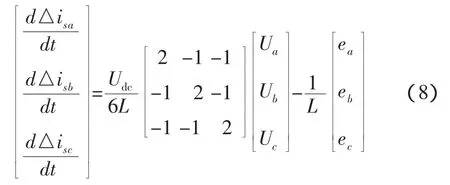
3 滑模变结构控制器设计
3.1 一般的滑模变结构控制

则切换函数定义为:
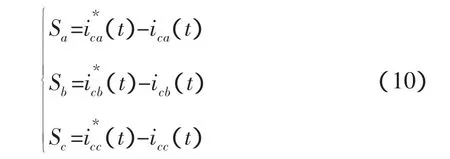
对于三相三线系统,式(10)中只有两个滑模子面方程是独立的,根据滑模变结构的可达性条件,满足,则

其中,Ua-con、Ub-con为A、B相的控制信号,于是可以得到APF滑模变结构控制的一般控制规律为:
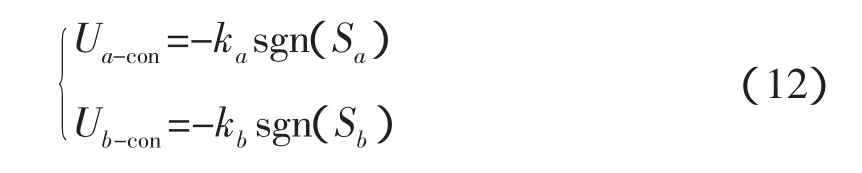
其中,
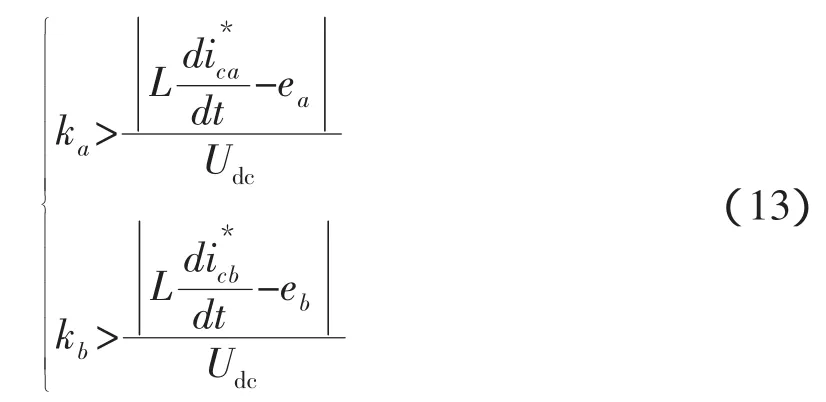
当假设 Sa>0,Sb>0 时,由式(8)的 SAPF 状态方程和式(12)的控制律可知:

满足以上关系的开关模式只有(0,0,l),因而以上APF滑模变结构控制律可以用表1表示(“+”、“-”为对应项正负符号)。
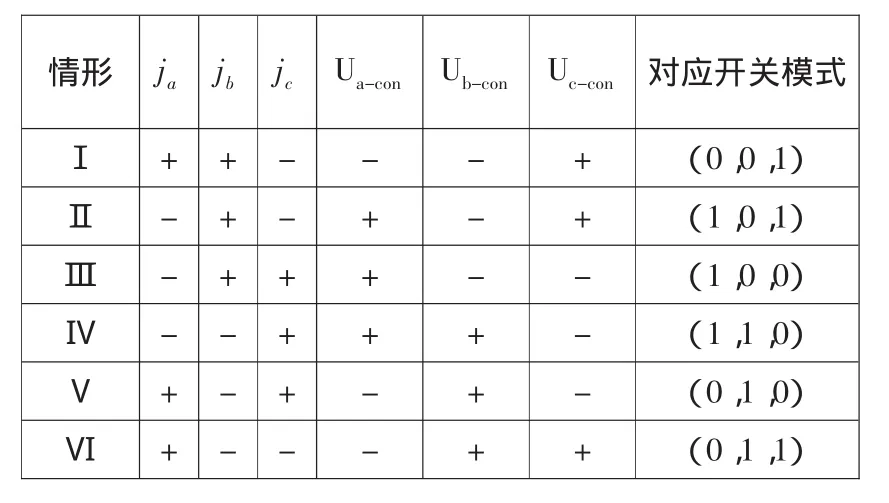
表1 APF滑模变结构控制律
由表1可知,在一个采样周期内只有一种开关模式,即某时刻决定的开关状态要到下一个时刻才会改变,因而最大开关频率不超过采样频率的一半[4]。注意到 ka、kb、kc均不大于 2 /3,同时也考虑到,由此可进一步得到SAPF电流完全可控的条件。

3.2 指数趋近律滑模变结构控制器设计
对于一个理想的滑模变结构系统,假设切换过程具有理想开关特性(即无时间及空间滞后),系统状态测量精确无误,控制量不受限制,则滑动模态总是降维的光滑运动,而且最终在有限时间内到达切换面。但对于现实的系统,由于滑模变结构控制在本质上的不连续开关特性,以及开关器件的时间滞后、空间滞后,系统的惯性、延迟,测量误差等因素的影响,使得系统的状态到达滑模面后,不是保持在滑模面上做滑动运动,而是在滑模面附近做来回穿越运动,甚至产生极限环振荡,这种现象称为抖振。在SAPF中抖振现象表现为电流开关纹波较大。
从物理意义上理解,产生抖振的原因是由于系统状态点以其固有的惯性冲向切换面时具有一定的速度。因此,可以为控制该速度而设计各种趋近律。指数趋近律滑模控制就是一个既可保持变结构控制对摄动的不变性又能减小抖振的方法。
设计趋近律的原则就是:在远离切换面时,系统状态点向切换面的运功速度较大,而接近切换面时,速度渐近于零。这样既可以保证滑动模态到达过程中的动态响应,又可以减弱控制信号的抖振。
通常的指数趋近律表达式为:
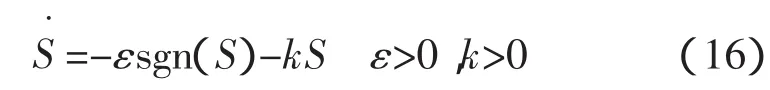
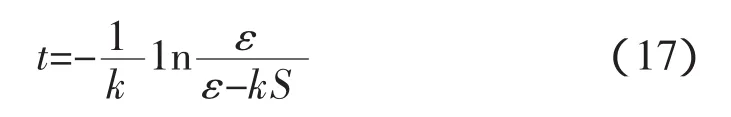
解得
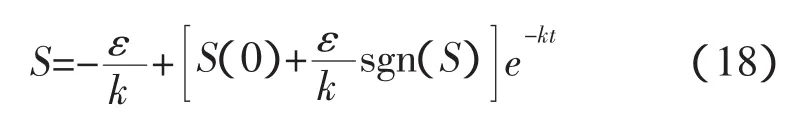
由分析可知,SAPF指数趋近律滑模变结构控制系统的切换函数为:
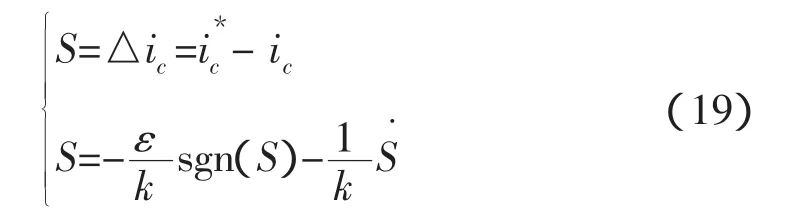
根据SAPF的数学模型,可设状态方程为:

整理得
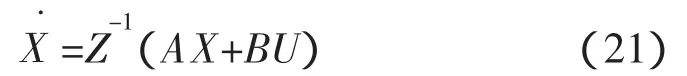
设切换面为 S(X)=CX,对切换平面 S(X)=CX 时间求导,得
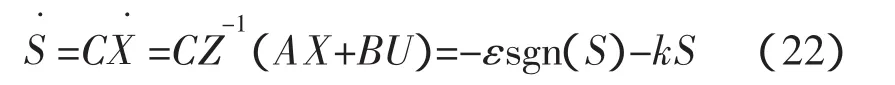
求解得控制律为:

其中,CB、Z均可逆。
4 仿真实验结果
本文在Matlab7.0环境下,利用Simulink工具箱对基于滑模变结构控制的SAPF进行计算机仿真,验证滑模变结构控制算法及控制器的正确性和有效性。
以A相为例,SAPF补偿前电流波形如图2(a)所示,补偿前的电流波形的FFT分析如图2(b)所示。
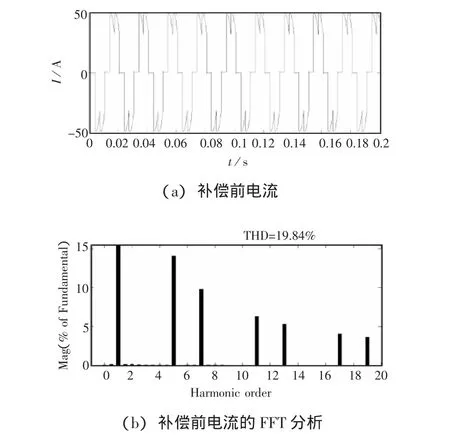
图2 补偿前的SAPF仿真波形
由图2(a)波形可以看出,补偿前负载电流含有大量谐波,使得负载电流发生了畸变。经过图2(b)的分析发现,总的电流畸变率为19.84%,5次谐波含量为 13.87%,7 次谐波含量为 9.98%,11 次谐波含量为 7.35%,13 次谐波含量为 5.62%,17 次谐波含量为4.29%。
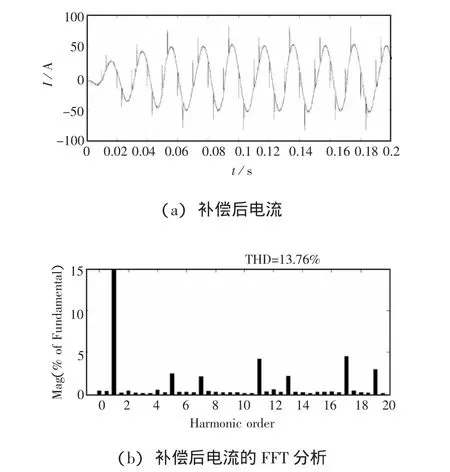
图3 指数趋近律控制下的SAPF仿真波形
采用指数趋近律滑模变结构对电流进行跟踪控制,仿真波形如图3所示。
由图3(a)所示的波形可以看出,SAPF采用指数趋近律滑模变结构电流控制方法时,补偿后的电源电流波形得到了极大改善,接近于正弦波。
经过图3(b)的分析发现,总的电流畸变率降为 13.76%,5 次谐波含量为 2.49%,7 次谐波含量为 2.08%,13 次谐波含量为 2.04%,11 次谐波含量为4.01%,17次谐波含量为4.67%。滤波后畸变率明显降低,谐波得到了极大控制。表明指数趋近律滑模变结构控制方法能对SAPF的电流进行有效的跟踪控制。
5 结论
通过仿真分析表明,所设计的指数趋近律滑模变结构控制系统能对电力系统中的典型谐波源进行有效补偿,且实现简单明了,能有效增强控制系统的稳定性,改善系统的动、静态性能。同时验证了SAPF在所设计的指数趋近律滑模变结构控制系统下对改善电网典型谐波源和电能质量影响的可行性和有效性。
[1]王兆安,杨 君,刘进军等.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2006.
[2]Bird B M,Marsh J F,McClellan P R.Harmonic reduction in multiple converters by triple-frequency current injection[J].Proc IEEE,2001,116(10):1730-1734.
[3]张昌凡,何 静.滑模变结构的智能控制理论与应用研究[M].北京:科学出版社,2005.
[4]Munoz D,Sbarbaro D.An adaptive sliding mode controller for discrete nonlinear systems[J].IEEE Transactions on Industrial Electronics,2000,47(3):574-581.
