电流型Z源逆变器的三值逻辑空间矢量控制策略＊

房绪鹏，朱明杰，谭延超

（山东科技大学信息与电气工程学院，山东青岛266510）

1 引言

Z源逆变器克服了传统电压源和电流源逆变器的不足，提供了一个新颖的功率变换概念，其主桥臂可开路或短路运行，具备直接升／降压功能［1］。Z源逆变器尤其适用于直流输入端电压波动较大的应用场合，如燃料电池等。目前对于电压型Z源逆变器的研究已经比较深入，电流型Z源逆变器的研究则处于刚起步阶段，而电流型Z源逆变器在电气传动、电力系统以及超导电力等场合具有广阔的应用前景。电压型逆变器的控制策略不能直接应用到电流型逆变器上，本文引入了三值逻辑控制策略，通过一个二-三逻辑转换电路，使得电压型Z源逆变器的控制策略能够过渡到电流型Z源逆变器，并由此提出了电流型Z源逆变器的三值逻辑空间矢量控制策略。

2 电流型Z源逆变器的三值逻辑控制

图1所示出电流型Z源逆变器的基本拓扑，直流电压源串联一个电感，输入侧相当于电流源。逆变桥开关采用全控型器件和功率二极管串联的形式，与传统电流源逆变器相同。对传统的电压源逆变器而言，在进行PWM控制时，其同一桥臂的上下两个开关器件有两种状态，即：

然而，在电流源逆变器的脉宽调制控制中，对同一桥臂的上侧和下侧开关器件而言，则存在着4种状态，分别是上通下断，上断下通，上下全通和上下全断。其中，后两种状态对于输出侧来说效果相同，都为零电流。为此需要构造三值逻辑开关函数Q，有：

图1 电流型Z源逆变器的主电路拓扑结构图

下面研究由传统二值逻辑信号产生三值逻辑信号的方法。由电流型逆变器工作时的开关状态，可以得出：

将上式展开，得

上式说明双极性二值逻辑开关函数Pj（j＝a，b，c）通过相应的线性结合可以表达三值逻辑开关函数Qj（j＝a，b，c），即

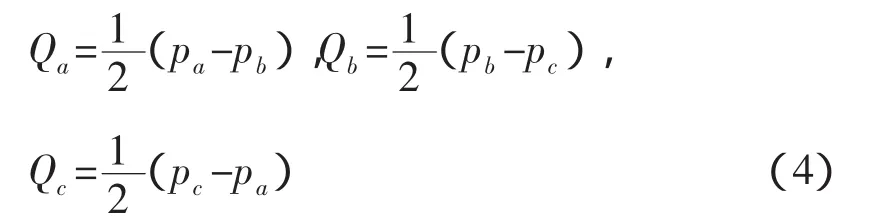
对于电流型Z源逆变器而言，可以在传统的直通零状态中插入开路零状态，即把关断6个开关管的开路零状态控制信号加入二-三逻辑转换表中。结果如表1所示。

表1 二-三逻辑状态转换表

关于开路零矢量的注入方法，成熟的电压型Z源逆变器的控制方法都可以应用到电流型Z源逆变器中来，如简单升压控制法，最大增益控制法，三次谐波注入法等。下文中将采用简单升压控制方法对电路进行仿真。

3 三值逻辑空间矢量的信号发生原理

可以利用空间矢量PWM技术实现三值逻辑空间矢量PWM信号的发生。

设iat，ibt，ict为电流源逆变器的交流侧电流瞬时值，进行坐标变换，将三相静止坐标系变换到两相静止坐标系，则在α β坐标系中的电流源逆变器的交流侧电流瞬时值写成矩阵形式：

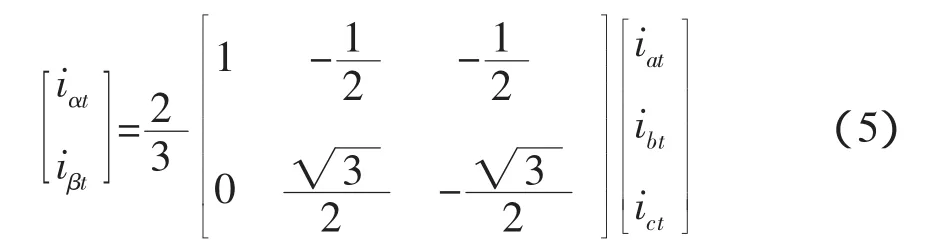
变换过程中α轴与a轴相重合。式（5）用复平面（α、β）的电流矢量描述为：

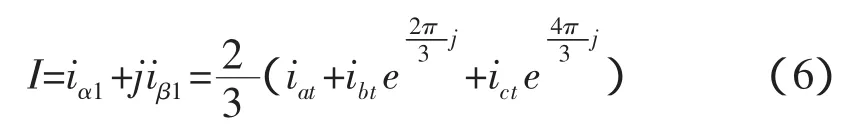
若假定电流源逆变器交流侧基波电流对称，且令：

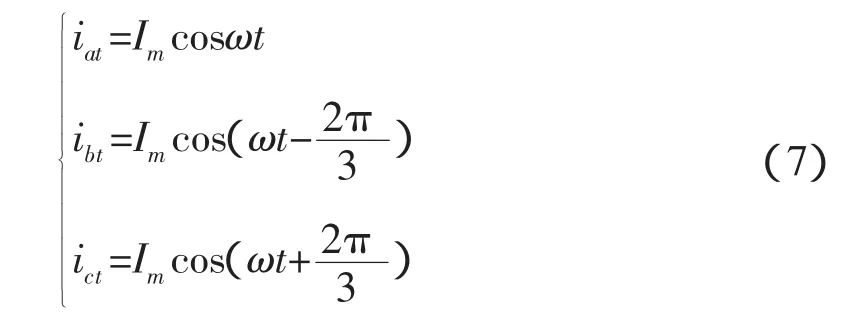
式中，Im为电流源逆变器交流侧基波电流幅值，将式（7）代入式（6）得：

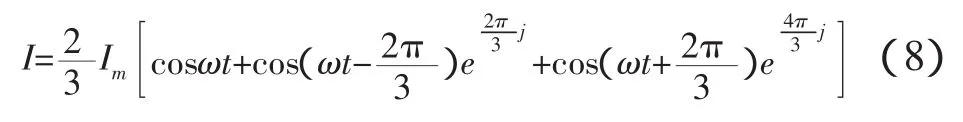
式（8）表明：用一个空间同步旋转电流矢量可以描述三相对称基波电流。

图2 三相CSI空间电流矢量的组成

把传统的二值逻辑空间矢量对应的开关状态经过二-三值逻辑转换之后可得对应的三相电流源逆变器的电流空间矢量，该矢量可用开关函数（Qa，Qb，Qc）的组合来描述，其构成如图2所示。

三相电流源逆变器的空间电流矢量可描述为：

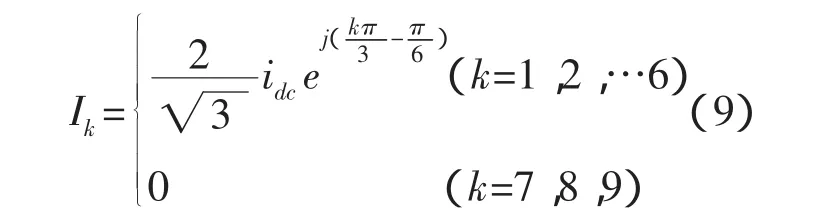
图3 三相电流源逆变器（CSI）空间电流矢量分布

三相电流源逆变器（CSI）的空间电流矢量分布如图3所示，利用电流源逆变器的9个空间电流矢量Ik（k＝1-9）按照一定的次序进行矢量合成，就可以得到指令电流矢量I，如指令电流矢量在扇区I范围内，则可以利用扇区I的两个边界矢量I1、I2来合成指令矢量。假如两个矢量I1、I2的作用时间分别为T1、T2，设脉宽调制的开关周期为TS，则有I1T1＋I2T2＝ITS。并且在边界矢量I1、I2的合成过程中根据需要插入零矢量，从而填补TS和T1＋T2之间的时间差，零矢量的作用时间为T0＝（TS-T1-T2）／2，开路零矢量可平均地插入传统零矢量中。

图4 矢量合成示意图

指令矢量的合成原理如图4所示，由三角形正弦定理得：

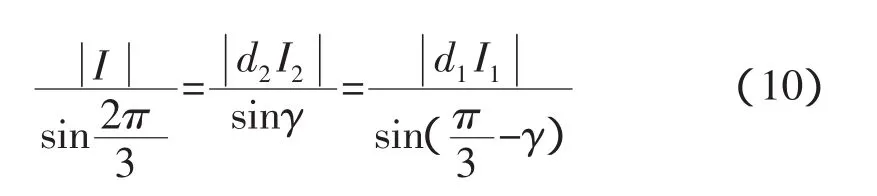
上式中，γ为指令矢量I和I1的夹角，并且有：

联立式（10）和式（11）得：

上式即为指令矢量合成的定量关系式。

电流源逆变器的零矢量有3种形式，分别为I0＝I7，I0＝I8，I0＝I9。为了使一个开关周期中开关器件的转换次数最少，必须使一个切换过程中只发生一对开关器件的切换，分析各个区域的开关状态，得出零状态选择结果如表2所示。

表2 区域对应零矢量表

4 Matlab仿真电路

根据上述的原理构建基于Matlab Simulink的仿真图，三值逻辑SVPWM产生模型如图5所示。

图5 三值逻辑空间矢量信号产生模型图

零状态选择模型如图6所示，其中零状态的选择由脉冲发生器来实现。上下桥选择电路如图7所示，开路零矢量选择电路如图8所示。

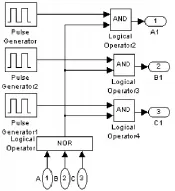
图6 零状态选择仿真模型图

图7 上下桥选择电路

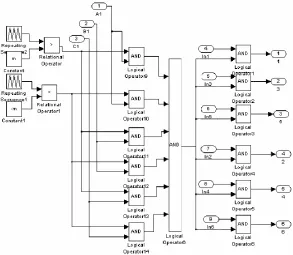
图8 开路零矢量选择电路

对于开路零矢量的注入，采用简单升压控制方法，将开路零矢量平均的插入传统零矢量的中间，开路占空比可由上图所示的constant模块来调节。将以上的各部分模块综合，可得到系统的控制信号生成模型如图9所示。

图9 控制系统仿真模型图

此外，根据电路的拓扑结构，修改元器件的参数，绘制系统的仿真主电路如图10所示。

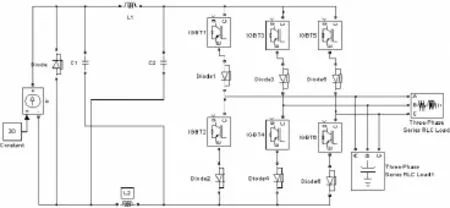
图10 系统仿真主电路

5 仿真实验结果

根据以上的分析进行仿真实验，仿真参数设置如下：Z 源网络 L1＝L2＝2mH；C1＝C2＝200μF；开关频率为3kHz，逆变器输入侧电流30A，输出功率P＝10kW，仿真波形如图11-13所示。图11为功率开关管的触发脉冲信号，从上往下依次为 S1、S2、S3、S4、S5、S6，图12为Z源网络电感电流，图13为输出的相电流和相电压波形。

图11 开关管对应的触发脉冲

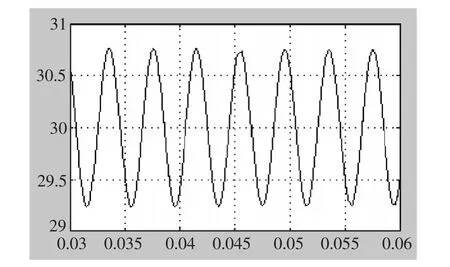
图12 仿真波形（Z源网络电感电流）

图13 空间矢量调制法的输出电流电压波形图

通过仿真结果可以看出，与普通的电流源逆变器相比，通过开路零矢量的引入，Z源逆变器具有升电流的特性，同时应用了三值逻辑SVPWM控制策略后，直流电流利用率得到了显著提高，且输出电流和电压波形的THD有所改善。

6 结论

本文将三值逻辑控制策略引入了电流型Z源逆变器，通过一个二-三值逻辑转换电路，将传统电压型Z源逆变器的控制信号转换成了电流型Z源逆变器的控制信号，从而将电压型和电流型Z源逆变器的控制统一起来，并由此提出了电流型Z源逆变器的三值逻辑空间矢量控制策略，最后通过Matlab的Simulink控制箱对控制电路进行了仿真，仿真结果与计算分析结果一致，证明了前述控制策略的合理性和可行性。

［1］Fang Zheng Peng，Z-Source Inverter，IEEE Transactions on Industry Applications，2003，39（2）：504-510.

［2］房绪鹏.Z源逆变器研究［D］.浙江：浙江大学，2005.

［3］张崇巍，张 兴.PWM整流器及其控制［M］.北京：机械工业出版社，2005.

［4］顾 斌等.Z源逆变器空间矢量控制的DSP实现［J］.电力电子技术，2005（12）：107-108.