变速恒频风力发电机组的模糊控制研究＊

刘庆雪，郭 涛 ，公茂法

（1.山东科技大学信息与电气工程学院，山东青岛266510；2.济宁能源发展集团有限公司义桥煤矿，山东济宁272511）

1 引言

高效、清洁、多样化是当今世界能源发展的潮流，中国经济持续发展，对能源的需求增长很快，常规能源的供应及其带来的环境问题日益突出，随着风电技术的发展和批量的增大，成本将会继续下降，必然成为重要的清洁能源。

然而由于风能具有能量密度低、随机性和不确定性等特点，使风力发电系统成为一个非线性、多变量、强耦合系统，大大降低了风力发电的效率以及可靠性和稳定性，从而导致发电成本升高，所以要对风力发电机加以行之有效的控制。

传统的PID控制器需要首先建立一个有效的系统模型，而由于风力发电系统的复杂性，系统模型的建立非常困难。而模糊控制不需要建立精确的数学模型，具有控制机理和策略易于接受和理解，设计简单，应用方便的特点，使得模糊控制非常适合于风力发电系统的建模和控制。本文的目的就是设计一种双馈风力发电机的模糊控制系统，在风速发生变化时，叶轮桨距角或发电机定子转速随之发生变化，将发电机的输出功率限制在额定值附近，并利用Matlab进行模拟系统仿真和优化［1-2］。

2 变速恒频双馈风力发电机控制的基本原理

根据感应电机定、转子绕组电流产生的旋转磁场相对静止的原理，可以得出变速恒频双馈风力发电机运行时电机转速与定、转子绕组电流频率关系的数学表达式。

式中：f1为定子电流频率，由于定子与电网相连，因此f1与电网频率相同；n1为定子旋转磁场的同步转速；p为电机的极对数；n为风力发电机的转速；f2为转子电流频率。

由式（2）可知，当风力发电机转速n发生变化时，若调节转子电流频率f2相应变化，可使f1保持恒定不变，即与电网频率保持一致，实现风力发电机的变速恒频控制。当n＜n1时，风力发电机处于亚同步速运行，变流器向转子提供交流励磁，定子发出电能给电网；当n＞n1时，风力发电机处于超同步速运行，此时定子和转子同时发出电能给电网；当n＝n1时，f2＝0，变流器向转子提供直流励磁，此时发电机作为同步电机运行［3］。

3 变速恒频双馈风力发电机的数学模型

变速恒频双馈风力发电机的等效电路如图1所示。

由图1可列出相应的基本方程为：

图1 变速恒频双馈风力发电机等效电路图

通过分析可知，转子可以运行于超同步速和亚同步速两种状态下，此时发电机能向外输出功率，电磁功率 PM＝m1U1I1cosφ1，机械功率转差功率，当转子处于亚同步速时，Ps＞0，转子从变频电源输入功率；当转子处于超同步速时，Ps＜0，转子向变频电源输出功率。无论哪种情况，输入机械功率总要克服电磁转矩做功，同时向定子传递功率［4］。

4 模糊控制系统的设计

被控对象是风机系统，如图2所示为风电系统的模糊控制示意图。

图2 风电系统的模糊控制示意框图

在高于额定风速的变桨距控制策略中，控制器的设计选用常用的二维模糊控制器，控制器的输入量为发电机功率偏差和功率偏差变化率。在模糊控制系统运行中，控制器的输入值、输出值是有确定数值的清晰量，而在进行模糊控制时，模糊推理过程是通过模糊语言变量进行的，在清晰量和模糊量之间有一定的对应关系。这种把物理量的清晰值转换成模糊语言变量值的过程叫做清晰量的模糊化。

4.1 语言变量隶属函数的确定

语言变量是以自然或人工语言的词、词组或句子作为值的变量。在高于风速的变桨距模糊控制器中，可以将功率偏差划分为“功率偏差负大”、“功率偏差负中”、“功率偏差负小”、“功率偏差负零”、“功率偏差正零”、“功率偏差正小”、“功率偏差正中”、“功率偏差正大”8个部分。“功率偏差”称为语言变量的变量值。语言值可用模糊集来描述。如图3所示为风机功率偏差变量的隶属函数，图3中对应于模糊控制器的每一语言变量，必须定义它的各个语言值，即它的各个模糊集的隶属函数。一个语言变量的各个模糊集（语言值）之间并没有明确的分界线，反映在模糊集的隶属函数曲线上，就是这些隶属函数必定相互重叠。在图3中，功率偏差既可属于“中”的范围，也可以认为是“低”的范围。

图3 风机功率偏差变量的隶属函数

在一个模糊控制系统当中，隶属函数之间的重叠程度直接影响着系统性能。选择合适的性能，是风机模糊节距控制器对于参数变化时具有鲁棒性的原因所在。隶属函数间不恰当的重叠可能最终导致模糊控制系统产生随意的混乱行为，一般重叠率在0.2-0.6之间取。语言变量可以任意地划分几个语言值，但并不是分得越多、越细，控制的精度就会越高。所以在设计模糊节距控制器中，初始划分的级数可取少些，在进一步优化时，根据情况再考虑增加。另外，可将三角形模糊集的“零”（ZE）固定在工作区上，而其它模糊集则向“零”靠拢，有助于提高系统的控制精度。

4.2 清晰量转化为模糊量

如图4所示为变桨距风力机模糊节距控制器系统框图。

它含有功率偏差e、功率偏差变化率△e两个输入量，和一个节距给定控制量u。它们都是清晰量。这3个物理量都要从物理论域通过量化转换到整个整数域，再在整数论域给出若干语言变量值，从而实现整个论域的模糊化过程。

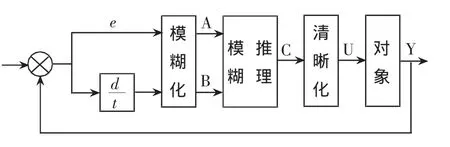
图4 风力机模糊节距控制器系统框图

对于偏差e，可以把其物理论域通过量化变换到整个论域 ｛-6，-5，-4，-3，-2，-1，0-，0＋，1，2，3，4，5，6｝ 并取｛“负大”，“负中”，“负小”，“正零”，“负零”，“正小”，“正中”，“正大”｝（NB，NM，NS，NZ，PZ，PS，PM，PB）8 个语言变量值档次。各个语言变量值的隶属函数可写成表1所示的值，即偏差的语言变量值赋值表。

表1 偏差e的语言变量值赋值表

对于偏差△e，可以把其物理论域通过量化变换到整个论域｛-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6｝，并取 ｛“负大”，“负中”，“负小”，“零”，“正小”，“正中”，“正大”｝（NB，NM，NS，ZE，PS，PM，PB）7 个语言变量值档次。各个语言变量值的隶属函数如表2的形式。

表2 功率偏差变化率△e

4.3 模糊控制器控制规则的设计

在设计模糊节距控制器的控制规则时，必须考虑控制规则的完整性、交叉性、和一致性。完备性值指对于任意给定的输入，均有相应的控制规则起作用。要求控制规则的完备性是保证系统能被控制的必要条件之一。控制器的输出值总由数条控制规则来决定，说明控制规则之间是相互联系、相互影响的。即控制规则之间的交叉性，可以产生复杂的控制曲面，得到更好的控制性能。其控制规则如表3所示。

表3 模糊控制规则表

5 风力发电机的Simulink仿真结果

如图5所示为模糊控制系统模型，信号源取阶跃信号，模糊控制器载入先前保存至工作区的高风速模糊控制器。该仿真旨在观测模糊控制器跟随性能。

图5 模糊控制系统模型

仿真的系统的发电机参数为额定功率P＝7.5kW，额定转速 n＝1500r／min，额定电压 U＝380V。其他参数为桨叶半径为R＝3.24m，转动惯量J＝3.5kg·m2，额定风速为 10m ／s。由于高阶系统的特性在一定条件下可以用二阶系统的特性来表示，被控对象的模型可以表示为：

根据变桨距功率控制一般要求误差小于额定功率的10%，即±10%。根据该规则可以设置增益量，量化因子即图5中的增益Gain、Gain1、Gain2，以使输入量恰好覆盖［-6，＋6］的范围。量化因子计算方法如下。

Kpe＝6：误差变化最大范围＝ Gain；Kcpe＝6：误差变化率范围＝Gain1；Ku＝6：输出变化范围＝Gain2。

模糊控制系统模型如图5所示。当风速分别为v＝6m／s和20m／s时，即风力发电机达到额定功率前，异步电动机的输出功率仿真分别如图6、7所示。

图6 风速V＝6m／s时异步电动机的输出功率

图7 风速V＝20m／s时异步电动机输出的功率

由仿真结果可以看出，模糊控制器能有效地抑制输出功率和发电机转速在起始阶段的超调和波动，且能较快地达到稳态，较好地实现控制要求。

［1］周燕莉.风力发电的现状与发展趋势［J］.甘肃科技，2009，24（9）.

［2］王长贵，崔容强，周 草.新能源发电技术［M］.北京：中国电力出版社，2003，19-27.

［3］Wang Zhixin，Jiang Chuanwen，Ai Qian，Wang Chengmi.The key technology of offshore wind farm and its new development in China［J］.Renewable and Sustainable Energy Reviews，2009（13）：216–222.

［4］Boubekeur Boukhezzar and Houria Siguerdidjane.Nonlinear Control of Variable Speed Wind Turbines without speed measurement［C］.Proceedings of the 44th IEEE Conference on Decision and Control and the European Control Confer ence，Seville，Spain.2005.12，1022-1025.