粒子拖尾长度对高频DPIV测量误差的影响

陈启刚，李丹勋，钟 强，王兴奎

（清华大学水沙科学与水利水电工程国家重点实验室，北京 100084）

粒子拖尾长度对高频DPIV测量误差的影响

陈启刚，李丹勋，钟 强，王兴奎

（清华大学水沙科学与水利水电工程国家重点实验室，北京 100084）

基于连续激光源的高采样频率DPIV系统在进行曝光时可能会产生粒子拖尾现象。明渠湍流试验和数值模拟试验结果显示，粒子拖尾长度的增加会导致平均流速减小和湍流强度增大。分析表明，导致平均流速误差的原因之一是诊断窗口边缘局部粒子图像的缺失，且图像缺失程度会随着粒子拖尾长度增加而增大，从而使平均速度随粒子拖尾长度增加而减小；粒子拖尾的另一个直接后果是增大了粒子图像的有效粒径，从而导致湍流强度增大。通过增大第二个诊断窗口的尺寸，进行相关函数标准化和相关系数补偿等方法，可以消除粒子拖尾长度引起的误差。

PIV；拖尾长度；连续激光源；误差；平均速度；湍流强度

0 引 言

PIV是一种无干扰全场测速技术，可以快速获取瞬时二维或三维流速场。自20世纪80年代以来，随着对示踪粒子、光学设备、成像系统、速度提取算法等研究的不断深入，传统的PIV技术日趋成熟。

目前，标准的商用DPIV系统是以两台交错工作的脉冲激光为光源，数字摄像机按双帧单曝光模式拍摄示踪粒子图片，采用移动、变形或多重迭代的诊断窗口，基于快速傅里叶变换（FFT）对两个诊断窗口进行互相关计算得到速度场，通过相关系数峰值亚像素拟合可以提高测量精度［1－3］。文献中对基于脉冲光源PIV 系统的误差分析全面而深入［4－11］。

在标准的商用DPIV系统中，粒子曝光时间等于脉冲持续时间，可以设置到ns量级，但受限于激光的脉冲频率，其采样频率一般低于50Hz［12］。为了满足对高频湍流研究的需要，基于高频率脉冲激光的TRPIV系统近年来得到了较快发展，但其价格昂贵且对同步设备要求极高，尚无法在明渠湍流研究领域推广普及。提高DPIV采样频率的另一个重要途径是采用连续激光代替脉冲激光［12－14］。在基于连续激光的DPIV系统中，采样频率由高速摄像机控制，但由于连续激光的强度低于脉冲激光，相机曝光时间（相机快门从打开到关闭的时间间隔）一般要长于脉冲激光源的脉冲持续时间。Sante等［15］在将基于连续激光的TR－PIV应用于旋转槽道流的测量时，其相机曝光时间为200～300μs。

随着曝光时间的增加，示踪粒子在成像过程中会出现拖尾现象。这一现象早就引起了研究者的注意，例如Prasad［2］和 Adrian［3］在有关PIV 的综述中对此就有所提及，最近Sante等［13］在将连续激光器应用于实际流动测量时，也注意到粒子会随着曝光时间的增加而产生拖尾现象。但是，目前还未见有系统分析粒子拖尾长度对DPIV测量误差影响的研究成果。

为深入研究粒子拖尾现象对DPIV测量精度造成的影响，首先应用基于连续激光源的高频DPIV对同一明渠湍流时均速度和湍流强度进行测量，对比不同曝光时间（拖尾长度）下测量结果的差异；然后，采用蒙特－卡罗随机模拟方法生成两帧粒子图像，分析拖尾长度对平均速度的影响；最后对粒子拖尾导致DPIV测量误差的原因进行分析，并提出消除这种误差的方法。

1 明渠湍流试验

1.1 试验条件

构建了基于连续激光源的高频DPIV系统，在不同曝光时间条件下，对同一明渠均匀湍流进行测量，分析拖尾长度对时均流速和湍流强度测量精度的影响。

试验水槽长11m、宽0.25m、高0.20m，可调坡降范围为0～0.01，观测段距上游进水口8m。PIV硬件系统由2W连续激光源、工业用高速摄像机和光学透镜构成，相机CCD大小为640pixel×480pixel，采样频率604Hz。流场计算采用基于FFT的互相关算法；采用二重网格迭代模式进行计算，最大诊断窗口尺寸为64pixel×16pixel，最小诊断窗口尺寸为16pixel×4pixel；采用式（1）进行三点高斯亚像素拟合以确定相关系数峰值的位置。

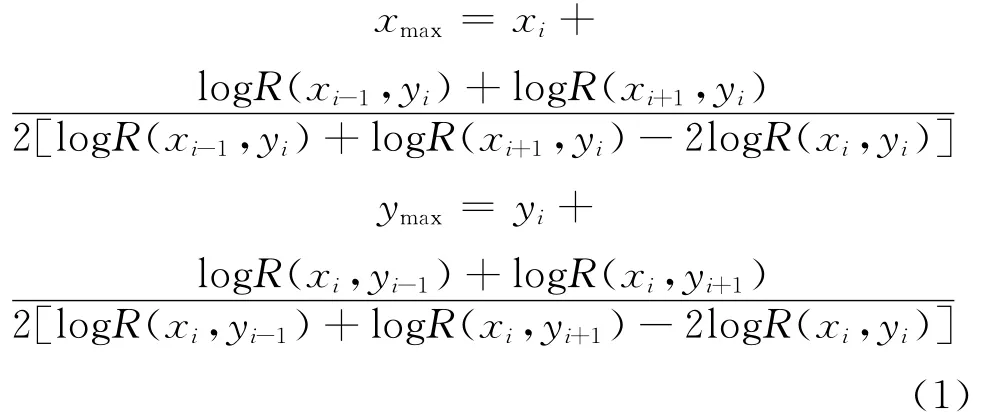
在相同的水流条件下进行了4组试验，相机分辨率Rs＝54.2μm／pixel，水深2cm，坡降0.4%，垂线平均流速49.7cm／s，摩阻流速u＊＝2.6cm／s，雷诺数Re＝8590。4组试验的曝光时间Te分别为300、600、1000、1500μs。每组试验均连续采集40000帧图片进行统计计算。其中，在曝光时间为300μs时，基本上无拖尾现象，可以作为对比的标准。

1.2 试验结果

定义拖尾长度L、平均流速Um、平均流速误差Rb、湍流强度等参数如下：

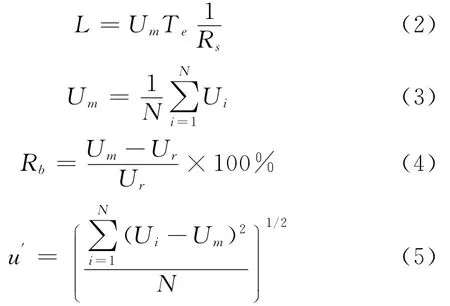
其中，Ui为单次采样得到的瞬时速度值，Ur为相同水流条件下300μs曝光时间（基本没有拖尾影响）的平均流速。

图1点绘了由（4）式计算的平均流速的误差。从图中可以看出，随着曝光时间的增加，平均流速减小，即平均流速随粒子拖尾长度的增加而减小；同时，近壁区速度梯度的存在进一步加剧了平均流速减小的幅度。

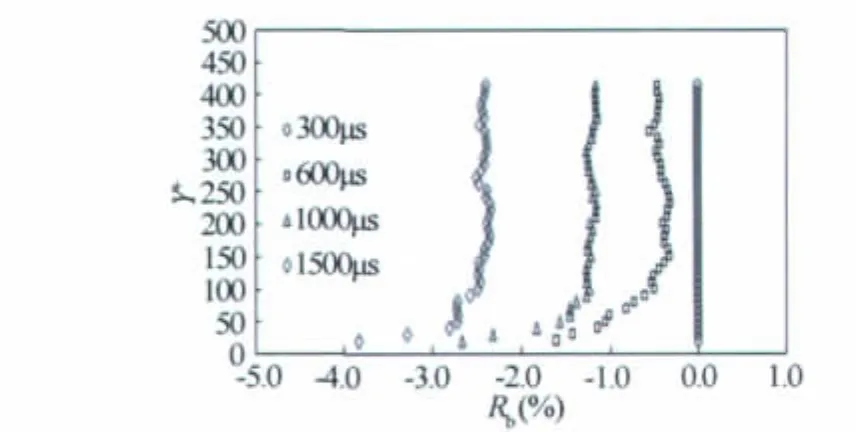
图1 平均流速误差沿水深的变化Fig.1 Mean－velocity error along water depth

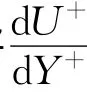
图4点绘了纵向湍流强度随曝光时间的变化，从图中可以看出，随着曝光时间的增加，纵向湍流强度有增大的趋势，这反映了粒子拖尾长度的影响。

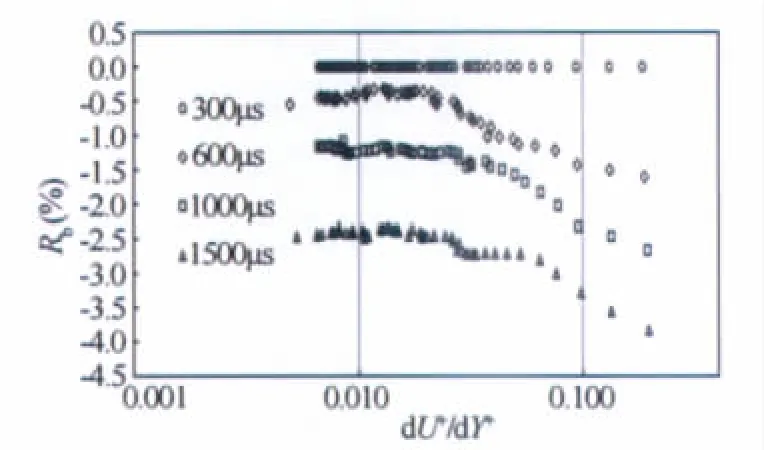
图2 平均流速误差随速度梯度的变化Fig.2 Mean－velocity error with respect to velocity gradient

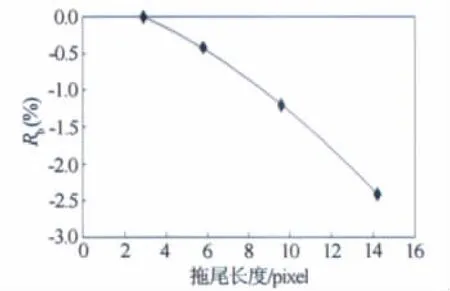
图3 平均流速误差随拖尾长度的变化Fig.3 Mean－velocity error with respect to tailing length

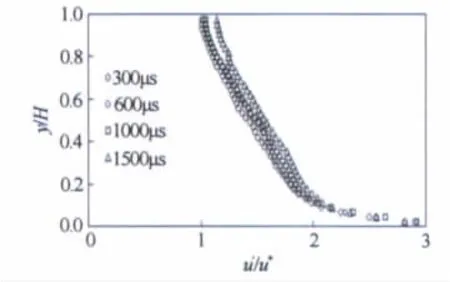
图4 纵向湍流强度随曝光时间的变化Fig.4 Streamwise turbulent intensity with respect to exposure time

2 数值模拟试验

2.1 图像生成

模拟均匀流场的情况。采用蒙特－卡罗模拟方法在400pixel×400pixel的图片上随机生成了一系列示踪粒子作为第一帧粒子图像（图5（a）），其中每个示踪粒子的大小为1个像素点；将第一帧图像中的每个像素点从左往右平行移动相同的距离，即为第二帧粒子图像，即每个诊断窗口均具有相同的纵向流速。为了模拟粒子的拖尾现象，只需在图5（a）中每个粒子的右边补充相同数量的粒子即可，图5（b）给出了图5（a）的粒子拖尾2个像素点后对应的图像。

2.2 数值模拟结果

共分析了拖尾长度为0～9的7种情况。模拟得到各种拖尾长度的粒子图像后，采用64pixel×64pixel的诊断窗口对粒子图像进行相关计算，将每个流场中得到的流速矢量求平均后即得到各拖尾长度条件下的平均流速。选择粒子无拖尾时的平均流速为参考流速Ur，用（4）式分别计算各拖尾长度条件下的平均流速与Ur的误差，计算结果如图6。

图5 模拟粒子图像Fig.5 Simulated particle images

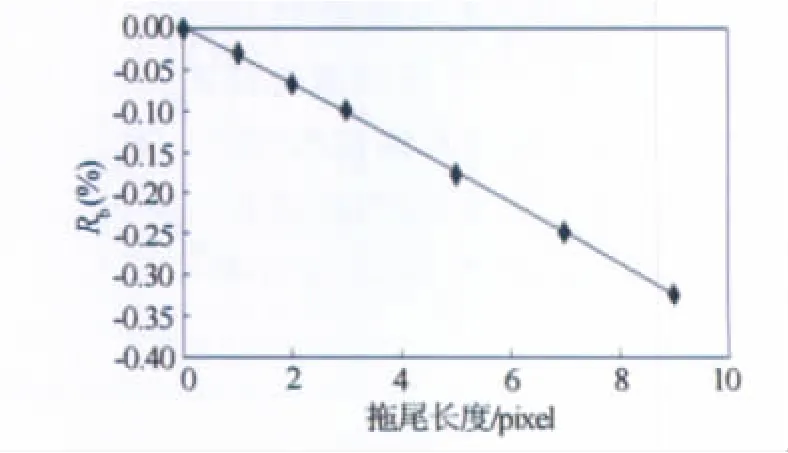
图6 平均流速误差的数值模拟结果Fig.6 Numerical simulation result of mean－velocity error

图6的结果表明，平均流速测量误差随着拖尾长度的增加而逐渐增大，这与图3中由试验得出的结果是吻合的。虽然图3和图6中二者的变化趋势是相同的，但在相同拖尾长度时，平均流速误差的数值有差别，这可能是由于湍流脉动及试验颗粒的三维运动特性等原因造成的，而基于简化的二维模拟图片进行PIV误差分析时一般会低估实际误差［9］。

3 误差分析

3.1 平均流速误差的原因

当粒子不发生拖尾时，经过8像素位移以后，第一个诊断窗口中离右边框8像素范围内的粒子将跑出第二个诊断窗口（如图7）。当粒子发生拖尾时，以拖尾2个像素为例，相当于粒子水平方向的粒径为原来的3倍，此时除了离右边框8像素范围内的粒子将跑出第二个诊断窗口以外，离右边壁8～10像素距离范围内的粒子图像将部分跑出第二个诊断窗口，导致粒子图像局部缺失（如图8），这是导致平均流速产生误差的原因之一。

为了验证以上分析，采用2.1节中已经生成的粒子拖尾2像素的图像进行计算，在计算之前，首先将第一帧诊断窗口中距离右边框10像素范围的粒子全部剔除，然后再与第二帧图片中相同位置的诊断窗口进行基于FFT的互相关运算。经过以上处理以后，可以保证粒子在拖尾长度不超过2像素时，第一帧诊断窗口中距离右边框大于8像素范围内的所有粒子图像均能完整的出现在位移8像素后的第二帧诊断窗口中，不致产生粒子图像的局部缺失。图9点绘了经过以上处理后得到的平均流速误差随粒子拖尾长度的变化趋势。

对比图6与图9可以发现，剔除距离右边框10像素范围内的示踪粒子后，当拖尾长度不超过2像素时，粒子拖尾不会导致平均流速误差。当拖尾长度超过2像素后，平均流速之所以再次产生误差，是因为距离右边框大于10像素的部分粒子又会产生图像的局部缺失。实际上，即使粒子不发生拖尾现象，当粒子图像的粒径大于1个像素时，也会因为诊断窗口右边缘的粒子图像局部缺失而导致平均流速误差。

如图10所示，当粒子图像均保持完整时，在将第一帧诊断窗口相对第二帧诊断窗口进行移动相关的过程中，由于实际位移点左右两侧的有效图像信息完全对称，FFT计算得到的最大相关点及其左右两个次最大相关点分布在以实际位移点为峰值的高斯曲线上，因此，按（1）式进行亚像素拟合不会使相关系数峰值偏离实际位移。当粒子图像存在局部缺失现象时，实际位移点左侧的图像信息量不变，而实际位移点右侧的有效图像信息量将会减少，这使得FFT计算得到的实际位移点右侧的相关系数偏小，亚像素拟合得到的相关系数峰值位置将偏向实际位移点的左侧，这是导致平均流速减小的原因。当粒子拖尾长度增加时，第二帧诊断窗口边缘缺失的图像信息量会增大，这是使得平均流速误差随拖尾长度增大而增大的原因。

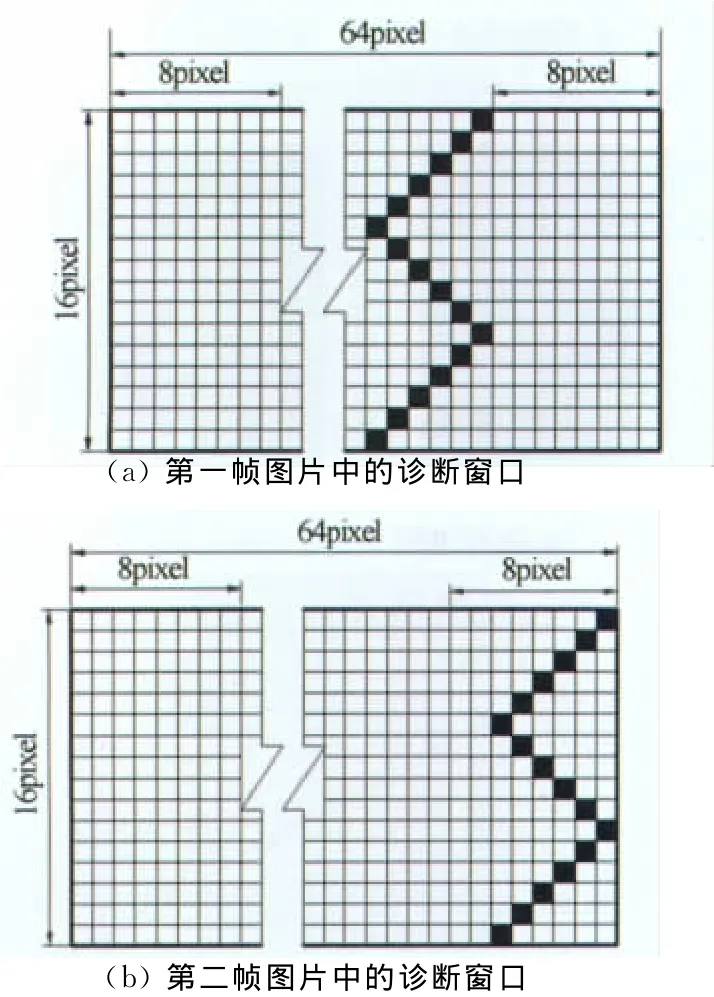
图7 无拖尾时粒子位移前后示意图Fig.7 Schematic diagrams of particles moving without tailing

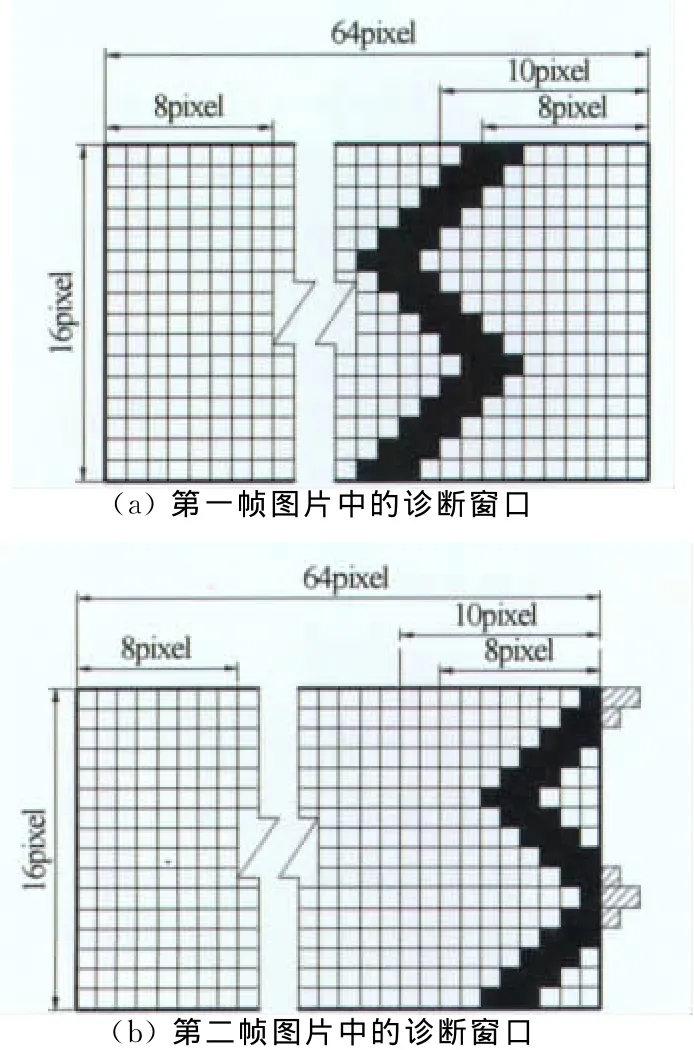
图8 拖尾2像素时粒子位移前后示意图Fig.8 Schematic diagrams of particles moving with two pixels'tailing

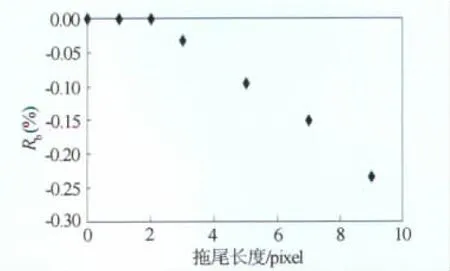
图9 剔除粒子后拖尾长度与平均流速误差的关系Fig.9 Relationship between mean－velocity error and tailing length after eliminating particles near the boundary

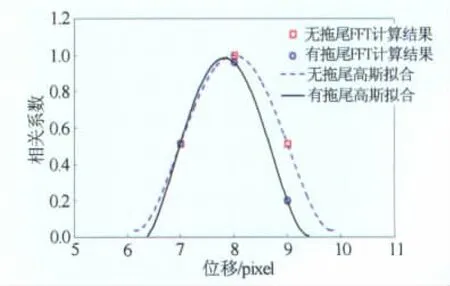
图10 基于FFT计算结果的高斯亚像素拟合示意图Fig.10 Schematic diagrams of Gaussian sub－pixel fit based on the result of FFT calculation

3.2 湍流强度误差产生的原因

根据 Adrain［16］，Willert［17］，Westerweel［6］等的研究，当粒子粒径大于2个像素后，计算得到的湍流强度会随着粒子半径的增大而增大。这是由于当粒子粒径增大时，FFT计算得到的相关系数峰值会变宽，在进行亚像素拟合时，相关系数峰值位置的波动幅度会增大，从而导致湍流强度增大。当示踪粒子出现拖尾时，等价于增大了粒子的有效粒径，因此，试验得到的湍流强度会呈现随拖尾长度的增大而增加的趋势。

3.3 消除误差的方法

上述分析表明，当粒子图像出现拖尾现象时，平均速度产生误差是由于第二个诊断窗口右边框附近的粒子图像局部缺失引起的；而拖尾导致湍流强度增大的原因在于增大了粒子的有效粒径。Anandarajah等［10］的研究表明，在进行互相关计算时，可以增大第二个诊断窗口的尺寸，使得第一个诊断窗口中的所有粒子均能完整的出现在第二个诊断窗口中，从而消除粒子图像局部缺失引起的平均流速误差。Huang等［7］的研究则发现，对相关函数进行标准化和对相关系数峰值附件的像素点处的相关系数进行补偿后，湍流强度将不再随粒径变化。

基于以上研究成果，可以通过以下方法消除粒子拖尾引起的DPIV测量误差。首先，采用大小不同的诊断窗口I1和I2（I2＞I1），按（6）式对互相关函数进行标准化后进行相关运算：

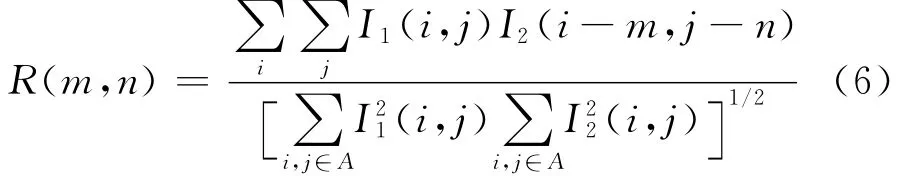
其中A是第一和第二帧诊断窗口在移动相关过程中的重叠区域。计算得到各整像素点处的相关系数后，设R（xi，yi）为像素点相关系数峰值，R（xk，yk）∈｛R（xi＋1，yi），R（xi－1，yi），R（xi，yi＋1，R（xi，yi－1）｝是R（xi，yi）周围用于亚像素拟合的四个相邻像素点的相关系数。采用（7）式对R（xk，yk）进行补偿后，再按照（1）式进行亚像素拟合，即可消除粒子拖尾引起的DPIV测量误差。

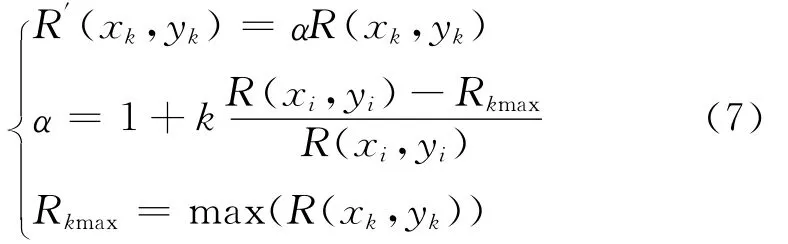
其中，k（0＜k＜1）为补偿系数。

4 结 论

对湍流等复杂流动的研究推动了基于连续激光源的高频DPIV系统的研发和推广，这种系统在对粒子图像进行曝光时可能会产生粒子拖尾现象。明渠湍流试验和数值模拟试验表明，随着粒子拖尾长度的增加，计算得到的平均速度会减小，而湍流强度则会增大。

由于诊断窗口边缘附近的粒子图像局部缺失，使得FFT计算的实际位移点及其右侧的相关系数偏小，最终导致高斯拟合后的相关系数峰值位置偏向左侧，从而使得计算得到的平均流速偏小，而粒子拖尾本身不会直接导致平均速度误差。当粒子拖尾长度增加时，图像局部缺失程度增加，FFT计算结果的不对称性加大，使得平均流速随拖尾长度的增大而减小。

粒子发生拖尾时，实际上相当于增大了粒子的有效粒径，等效粒径的增大是导致计算湍流强度增大的原因。

通过增大第二个诊断窗口，对相关函数进行标准化以及对相关系数峰值附近像素点处的相关系数进行补偿，可以避免平均速度误差的产生，也可使得湍流强度不随粒子粒径的增大而增加，从而消除拖尾长度对PIV测量误差的影响。因此，将基于连续激光源的高频DPIV系统应用于实际流动的测量是可行的。

［1］WILLERT C E，GHARIB M.Digital particle image velocimetry［J］.Experiments in Fluids.1991，10（4）：181－193.

［2］PRASAD A K.Particle image velocimetry［J］.Current Science，2000，79（1）：51－60.

［3］ADRIAN R J.Twenty years of particle image velocimetry［J］.Experiments in Fluids，2005，39（2）：159.

［4］GUEZENNEC Y G，KIRITSIS N.Statistical investigation of errors in particle image velocimetry［J］.Experiments in Fluids，1990，10（2－3）：138－146.

［5］KEANE R D，ADRIAN R J.Theory of cross－correlation analysis of PIV images［J］.Applied Scientific Research，1992，49（3）：191－215.

［6］WESTERWEEL J.Fundamentals of digital particle image velocimetry［J］.Measurement Science ＆ Technology，1997，8（12）：1379－1392.

［7］HUANG H，DABIRI D，GHARIB M.On errors of digital particle image velocimetry［J］.Measurement Science ＆ Technology，1997，8（12）：1427－1440.

［8］FORLITI D J，STRYKOWSKI P J，DEBATIN K.Bias and precision errors of digital particle image velocimetry［J］.Experiments in Fluids，2000，28（5）：436－447.

［9］WESTERWEEL J.Theoretical analysis of the measurement precision in particle image velocimetry［J］.Experiments in Fluids，2000，29（Supplement 1）：S3－S12.

［10］ANANDARAJAH K，HARGRAVE G K，HALLIWELL N A.Digital particle image velocimetry：particle image error（PIE）［J］.Journal of Physics：Conference Series，2006，45（1）：174－185.

［11］CARR Z R，AHMED K A，FORLITI D J.Spatially correlated precision error in digital particle image velocimetry measurement of turbulent flow［J］.Experiments in Fluids，2009，47（1）：95－106.

［12］王龙，李丹勋，王兴奎.高帧频明渠湍流粒子图像测速系统的研制与应用［J］.水利学报，2008，39（7）：781－787.

［13］DI Sante A，THEUNISSEN R，VAN den Braembussche R A.A new facility for time－resolved PIV measurements in rotating channels［J］.Experiments in Fluids，2008，44（2）：179－188.

［14］余俊，万津津，施鎏鎏，等.基于连续式激光光源的TR－PIV测试技术［J］.上海交通大学学报，2009，（8）：1254－1257.

［15］SANTE A D，CASTANO J G，BRAEMBUSSCHE R A V.Time resolved PIV in a rotating diverging channel：13th Int Symp on Application of Laser Techniques to Fluid Mechanics［Z］.Lisbon：2006.

［16］ADRIAN R J.Particle－imaging techniques for experimental fluids mechanics［J］.Annual Review of Fluid Mechanics，1991，23（1）：261－304.

［17］WILLERT C.The fully digital evaluation of photographic PIV recordings［J］.Applied Scientific Research，1996，56（2－3）：79－102.

陈启刚（1987－），汉族、四川宜宾人，博士研究生，主要从事明渠湍流和泥沙运动试验研究。通讯地址：北京市海淀区清华大学水利系泥沙研究所（100084）；联系电话：15120001870；E－mail：cqg09＠ mails.tsinghua.edu.cn

Bias error induced by particle tailing in DPIV measurement

CHEN Qi－gang，LI Dan－xun，ZHONG Qiang，WANG Xing－kui
（State Key Laboratory of Hydroscience and Engineering，Tsinghua University，Beijing 100084，China）

The presence of particle tailing affects the performance of DPIV systems that use continuous wave laser as light source.Open－channel flow experiments and numerical stimulations show that the measured mean velocity of the flow decreases and the turbulent intensity increases when the exposure time prolongs.Underestimation of the mean velocity is due to the fact that the existence of particle tailing aggravates the partial lost of particle images near the boundary of the interrogation windows.Overestimation of the turbulent intensity is caused by the enlargement of the seeding particles due to particle tailing.An algorithm was proposed to eliminate or reduce these errors by enlargement of the second interrogation window，normalization of correlation function and complementation for integer peak neighbors.

particle image velocimetry；particle tailing；continuous wave laser；error；mean velocity；turbulent intensity

O352

A

1672－9897（2011）06－0077－06

2010－11－24；

2011－08－12

国家自然科学基金（50779023）