5000m特大跨度悬索桥空气动力稳定性风洞试验研究

邵亚会，葛耀君，柯世堂，杨詠昕

（1.合肥工业大学土木与水利工程学院，合肥 230009；2.同济大学土木工程防灾国家重点实验室，上海 200092）

5000m特大跨度悬索桥空气动力稳定性风洞试验研究

邵亚会1，2，葛耀君2，柯世堂2，杨詠昕2

（1.合肥工业大学土木与水利工程学院，合肥 230009；2.同济大学土木工程防灾国家重点实验室，上海 200092）

伴随跨海大桥建造时代的来临，特大跨度悬索桥的空气动力性能研究日益紧迫，设计了中跨跨度为5000m的宽开槽和窄开槽钢箱梁悬索桥方案，实现了5000m特大跨度钢箱梁悬索桥的节段模型风洞试验，研究了宽开槽和窄开槽两种方案的颤振性能，识别了其颤振导数、颤振风速、颤振频率、三分力系数等重要参数；其次在风洞试验中研究了多种稳定板组合方案对窄开槽钢箱梁的颤振控制作用，发现中央稳定板和上稳定板的组合能将颤振临界风速提高50%；最后提出了适用于特大跨度悬索桥的二维颤振Straight－forward Method分析方法，对风洞试验进行了数值模拟，验证了该方法和节段模型风洞试验对于5000m悬索桥分析结果的一致性。最终研究认为：中央开槽达到足够宽度的方案与窄开槽附加稳定板的方案都能为跨度5000m的悬索桥提供足够高的颤振失稳临界风速，并能满足世界上绝大多数台风区的要求。

二维颤振；特大跨度悬索桥；直接分析方法；气动稳定性；风洞试验

0 引 言

21世纪，新一轮建造更大跨度桥梁的跨海连岛工程正在酝酿或实施［1－2］，以中国为例，其地处太平洋西岸，海岸线长4500km，江河入海口众多，三大海峡交通工程和主要江河入海口交通工程的建设在近年来逐渐提上议事日程［3］，主要有：中国沿太平洋高速公路工程（跨越渤海海峡、长江口、杭州湾、珠江口和琼州海峡）、舟山连岛工程、台湾海峡工程。

悬索桥跨径记录保持时间最长的为金门大桥，从1937～1964年长达27年，保持时间第二长的为威廉姆斯伯格桥，从1903～1924年长达21年。综合自1826年以来悬索桥跨径的演变历程，图1给出了悬索桥跨径记录随历史年代的变化，并按照五次曲线拟合了跨径与时间的关系，预测了2012～2050年约40年内悬索桥跨径增长趋势。按照目前的发展速度，在未来的几十年中悬索桥跨径将达到惊人的10000m，这里暂不考虑材料、技术、造价、政治等其它因素的制约。位于风环境中的特大跨度悬索桥其空气动力和静力稳定性直接关系到生命安全，对特大跨度悬索桥的抗风稳定性能的研究十分紧迫。

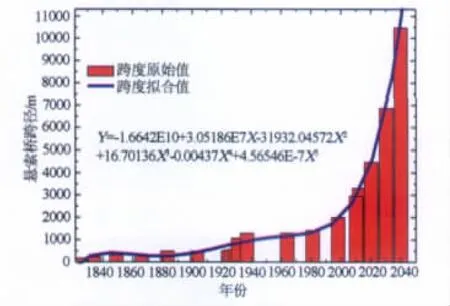
图1 悬索桥的跨径记录拟合与预测Fig.1 Span fitting and prediction of suspension bridges

在已有特大跨度悬索桥的设计思想指导下，提出了两塔三跨式5000m特大跨度钢箱梁悬索桥的设计方案，并通过节段模型风洞试验方法，检验了各方案的空气动力稳定性，最后提出了适用于特大跨度悬索桥二维颤振分析的Straight－forward method，与风洞试验结果相互校核，该方法的计算效率高，无频率迭代误差，对于颤振临界风速和颤振频率的计算与风洞试验结果吻合良好。

1 5000m悬索桥方案设计

K.Kazama［4］认为对于桁架梁悬索桥，单纯提高加劲梁竖向或侧向刚度对提高悬索桥整体的颤振失稳临界风速几乎没有作用，而当提高加劲梁扭转刚度为原来的2倍时，颤振临界风速可提高20%；提高主缆强度为原来的1.2倍时，颤振临界风速不变，即通过改变主缆强度提高颤振临界风速的措施是不现实的；提高桥塔刚度为原来的2倍时，颤振临界风速仅仅升高6%。葛耀君、项海帆［1］的研究结论认为：对于特大跨径的悬索桥来说，主缆的刚度主要取决于主缆的面积，而主缆的面积要从满足自身静力设计的要求出发；加劲梁对整体扭转刚度的贡献要比对整体抗弯刚度的贡献要大，但是5000m跨径的悬索桥，加劲梁的刚度却大大受到了限制；桥塔的刚度主要影响结构整体的竖弯刚度，对侧弯和扭转刚度的影响甚小。

因此，设计特大跨度悬索桥方案时，从空气动力稳定性的角度看，不必刻意提高加劲梁刚度、主缆刚度和强度以及桥塔的刚度。基于上述设计思想，并受直布罗陀海峡桥和墨西拿海峡桥的诸多设计方案的启发［5－6］，设计了中跨跨径为5000m的两种加劲梁开槽方案悬索桥，每种方案各设计了4种矢跨比的分方案，加劲梁断面形式如图2所示，加劲梁与主缆的主要参数如表1所示，基本自振频率如表2所示。

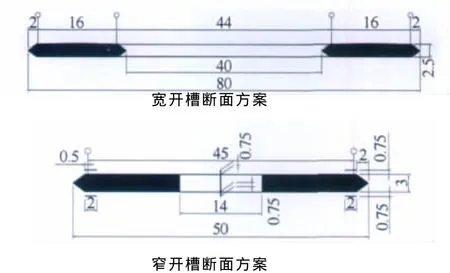
图2 5000m悬索桥加劲梁设计方案Fig.2 Trial design of girders for suspension bridge with a main span of 5000m

2 风洞试验模型加工

试验选取5000m跨度悬索桥的第一阶正对称竖弯和第一阶正对称扭转作为二维节段模型风洞试验的模型设计依据。因5000m特大跨度悬索桥的节段模型加劲梁宽度较大，高宽比很小，加工主要难点在于如何保证模型的整体和局部刚度，尤其是保证宽开槽加劲梁的横向刚度，为此采取了以下措施：

表1 加劲梁与主缆的主要截面参数Table 1 Main parameters of girder and cable

表2 基本自振频率Table 2 Natural frequencies of the trial design

（1）铝合金的焊接：采用铝合金搅拌摩擦焊，它是一种固态连接工艺，焊接时不会出现熔焊时的各种缺陷，接头性能良好。焊接前，先搭建模具，严格按照铝合金芯梁的最终成型状态搭建焊接模具，保证焊接的精度和可靠度，同时也保证了模型骨架的刚度，如图3所示。芯梁端部采用型材进行加强，保证其和端板连接时的强度和稳定性，这对于宽开槽断面尤为重要。

图3 焊接模具的架设Fig.3 Erection of the welding mold

（2）采用细木工板雕刻各种形状的镂空夹板，采用榫卯结构将其固定于模型芯梁的周围，镂空夹板在提高模型整体刚度的同时，减轻模型整体质量。夹板的高精度切割和拼装，也大大降低了模型阻尼比，试验证明模型总阻尼比为0.39%，如图4所示。加劲梁外衣由椴木切割而成，刚度大且密度小，也保证了模型的整体刚度。

（3）稳定板有两种制作模式，一是全部采用ABS板雕刻，二是采用轻质铝合金切割。防撞护栏和人行道栏杆采用ABS板雕刻。水平稳定板与栏杆等附属构件均通过全螺纹螺丝定位于桥面板上，中央稳定板则通过卡槽固定于桥梁的中轴线上，可拆卸。

（4）风嘴为智能化风嘴，全部可拆可换，通过细长螺丝将其与加劲梁主体结构拼接为整体，方便在气动措施控制研究中进行方案对比。

加劲梁节段模型测振试验模拟结构竖向和扭转方向两个自由度的振动特性，水平来流方向即阻力方向的振动特性没有模拟。节段模型采用几何缩尺比为1∶80，为了提高窄开槽断面的空气动力性能，设计了配套使用的中央稳定板，上水平稳定板，下水平稳定板和可拆卸调换的智能化风嘴。这里需要说明的是，对于宽开槽和窄开槽两种加劲梁断面形式，两者的单侧加劲梁的质量和质量惯矩是相同的，横梁的质量和质量惯矩也是完全相同的，唯一不同的是两种断面形式中横梁的长度。

3 风洞试验过程与结果

节段模型测振试验是在同济大学土木工程防灾国家重点实验室TJ－2边界层风洞中进行的，主要测振试验设备如下：TJ－2边界层风洞，高2.0m，宽2.5m，长30m，可调风速1～68m／s；压电式加速度传感器：CA－YD－103型；六通道测振放大器：YE5866电荷放大器；四通道动态信号分析仪：HP35670A信号分析仪；计算机采样系统：NI采样板，计算机以及相应软件；底支式五分量高频测力天平；供桥直流稳压电源。

3.1 窄开槽断面测振试验结果

对于窄开槽断面，分别进行了中央稳定板和水平稳定板的多种组合方案的颤振导数识别和颤振性能研究。窄开槽断面方案的颤振临界风速如表3所示，其中含上稳定板的两种方案效果最好，颤振临界风速最高，达到60m／s，说明上水平稳定板的颤振控制效果最佳。因此对于上稳定板方案，进行了详细研究，分别进行了包括防撞护栏和检修车轨道的5种风迎角下的颤振导数识别试验，研究发现颤振临界风速最高可达68m／s，负迎角时的效果较差，如表3所示。在整个试验过程中，获得的颤振导数如图5所示。

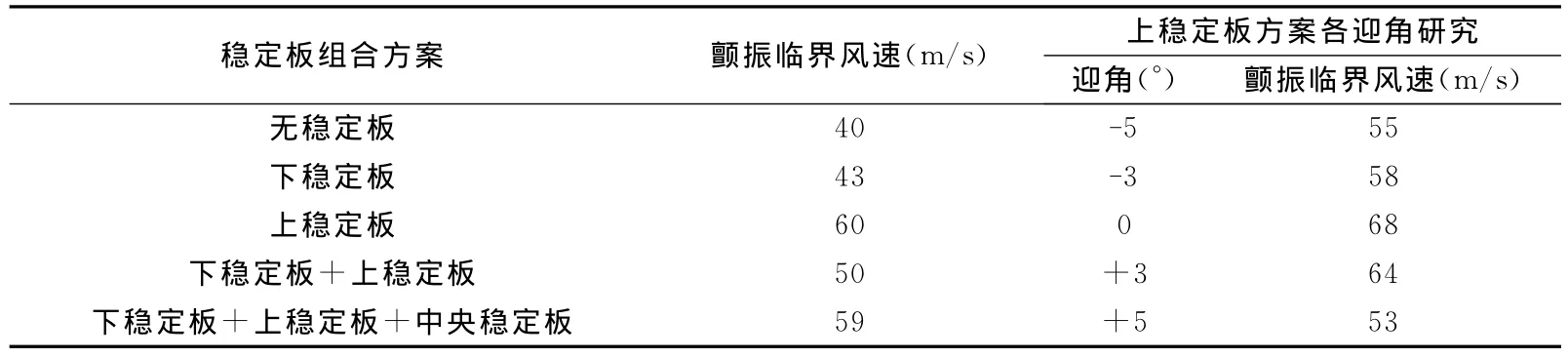
表3 窄开槽断面测振风洞试验结果Table 3 Wind tunnel test results for narrow slotted girder

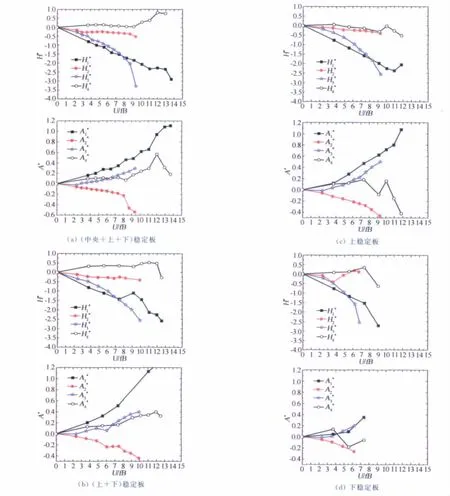
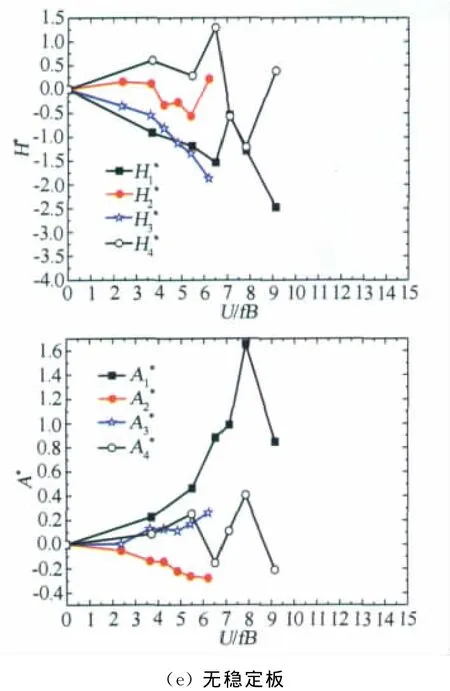
图5 窄开槽加劲梁方案各种稳定板组合工况颤振导数Fig.5 Aerodynamic derivatives of narrow slotted girder with the combination of stabilizers

3.2 宽开槽断面测振试验结果

对于宽开槽断面，分别检验了0°、±3°、±5°三个迎角下的颤振稳定性，颤振临界风速均大于80m／s，证明了宽开槽断面在5000m悬索桥中的可行性。试验过程中，获得的颤振导数如图6所示，需要说明的是，这里只识别了0°迎角下的颤振导数，一是因为宽开槽断面的宽度较大，当设置初始迎角时，断面边缘两侧的相对位移较大，容易导致模型侧翻；二是因为5000m方案的悬索桥，整体刚度很小，高风速时模型的初始位移较大，易使弹簧退出工作状态，故而只好放弃较大迎角下的颤振导数识别，这是自由振动衰减法识别颤振导数的局限性。对于宽开槽和窄开槽方案，颤振发生时均为竖弯和扭转强烈耦合的颤振形态。

测力试验获得的三分力系数如图7所示，分别为窄开槽断面和宽开槽断面在成桥运营阶段的三分力系数。

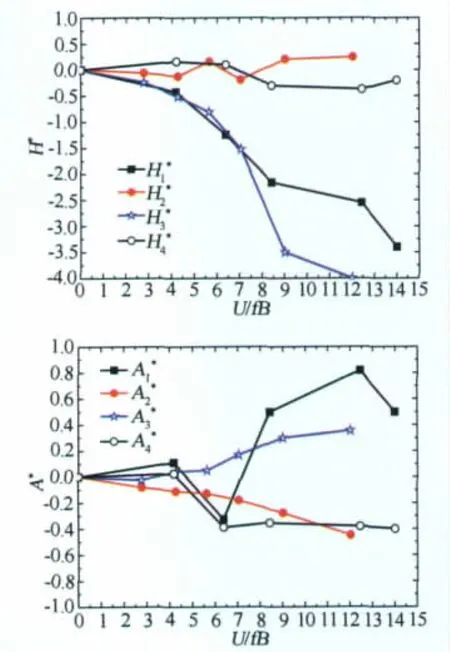
图6 宽开槽断面颤振导数Fig.6 Aerodynamic derivatives of wide slotted girder

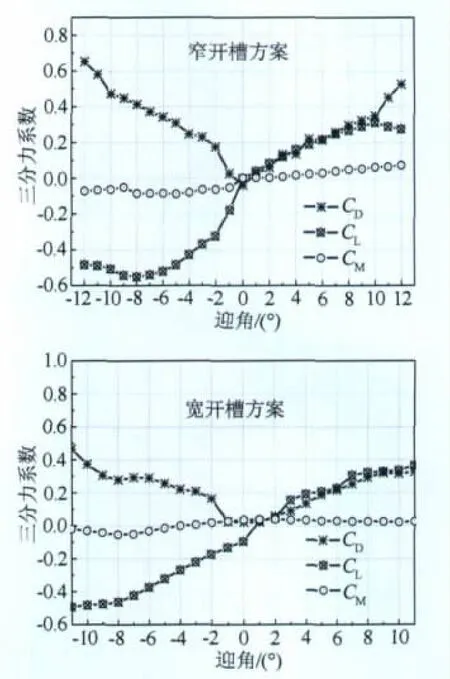
图7 成桥状态三分力系数Fig.7 Three coefficients in completed bridge state

4 Straight－forward Method颤振性能分析

传统复模态特征值分析方法［7－10］（CEVA）解决二维颤振问题时，颤振频率的求解需对频率进行预先选取和循环迭代，这种做法的缺点为：特大跨度悬索桥扭弯频率比接近于1时，可能导致频率迭代不收敛的情况；迭代运算的时间较长。为改进上述算法的缺点，本文基于传统复模态特征值分析方法和费拉里求解一元四次方程的思路，提出了特大跨度悬索桥二维颤振直接分析方法（Straight－forward method），该方法在特大跨度悬索桥二维颤振分析中无需频率迭代，计算时间短。传统的复模态颤振分析方法（CEVA－Conventional Complex Eigenvalue Analysis）求解颤振临界风速和颤振频率的搜索过程中，有两重迭代，包括频率的迭代（为了搜索与之对应的颤振导数）和各级风速的迭代（为了寻找颤振临界风速值），假设搜索的频率级数为20，每级风速下频率的搜索次数为20，则完成一次颤振全过程分析需要400次迭代。而对于Straight－forward method，假设搜索的频率级数为20，每级风速下频率的计算次数只为1，则完成一次颤振全过程分析需要20次迭代，计算效率相差20倍。从计算的时间来看，直接分析方法即使完成1000个风速级数的迭代，计算时间也不超过30s，大大简化了二维颤振分析的步骤，同时也更适用于特大跨度悬索桥的颤振性能研究。

二维颤振分析模型有竖向h和扭转向α两个自由度，运动方程为［11］：

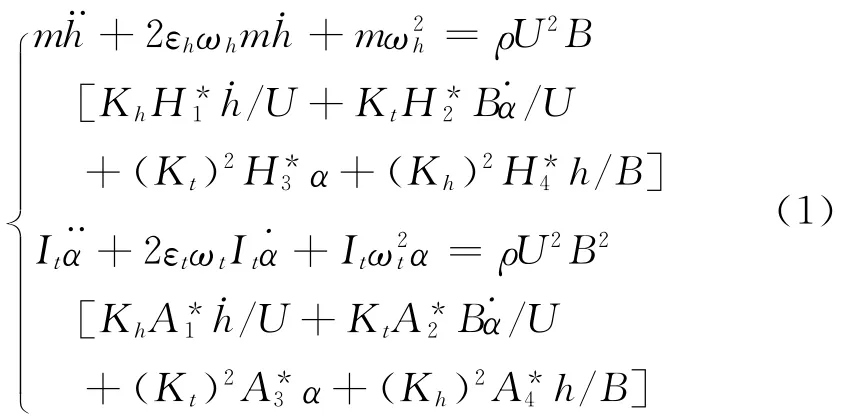
其中，m和It为节段模型延米质量和质量惯矩；kh和kt分别为竖弯和扭转刚度；ch和ct分别为竖弯和扭转阻尼比；L和M 分别为延米气动升力和升力矩；ρ为空气密度；U 为来流平均风速；B为桥梁宽度；K＝Bω／U，是无量纲折减频率；ω为振动圆频率；h和α分别为桥梁断面的竖向和扭转位移；H＊和A＊分别为竖弯向和扭转向气动导数。二维颤振问题转化为求解二维复特征值问题，即转化为求解式（1）的复特征值和特征向量问题，最终转化为求解如下一元四次方程的问题：

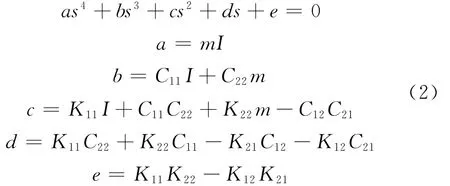
求解该方程的步骤分为：

第一步：将方程转化为无三次项的四次方程

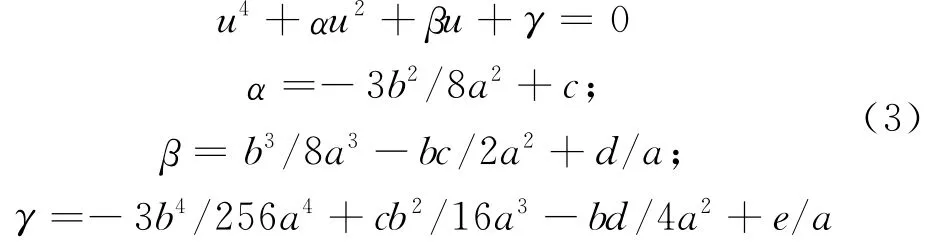
第二步：将方程转化为三次方程

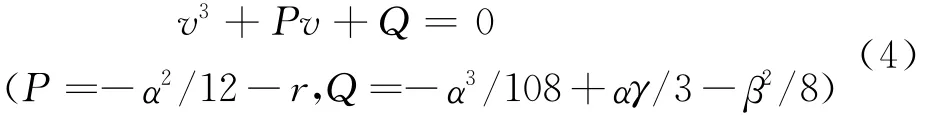
第三步：求解三次方程

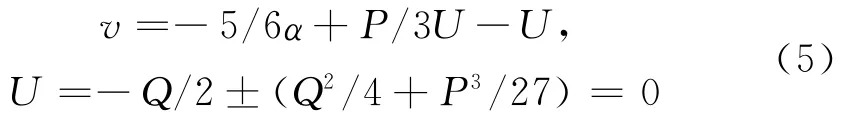
第四步：得到四次方程的通解

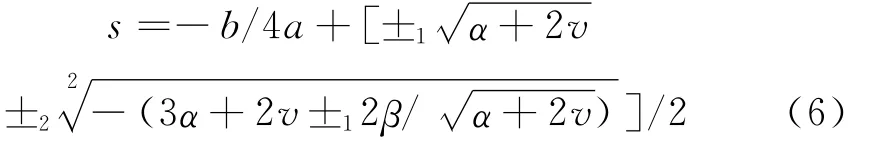
求解出特征值和特征向量之后，即得到了二维颤振系统随风速变化的振动频率和振动阻尼比，而振动系统在颤振发散状态之前的每个时刻的运动方程的通解可以表达为：

采用上述方法和风洞试验识别的颤振导数，对窄开槽和宽开槽方案的多种试验工况进行了二维颤振性能分析，得到的主要颤振临界风速和频率如表4和5所示。研究发现：无论是宽开槽断面方案还是窄开槽方案，矢跨比对于颤振临界风速和颤振频率的影响均不大；对于窄开槽加劲梁方案，上稳定板和上稳定板与中央稳定板组合方案的颤振控制效果最佳，比无稳定板时的颤振临界风速提高约50%，下稳定板的颤振控制效果不明显；对于宽开槽加劲梁方案，颤振临界风速在多个迎角下均大于80m／s。以上所有的计算工况中，均未出现频率迭代不收敛的情况，且计算时间短，计算效率高。

表4 窄开槽断面颤振性能分析Table 4 Flutter performance of narrow slotted girder

表5 宽开槽断面颤振性能分析Table 5 Flutter performance of wide slotted girder

5 试验结论

对5000m特大跨度两塔三跨式钢箱梁悬索桥的空气动力稳定性进行了详细的风洞试验研究，得出了如下结论：

（1）实现了5000m特大跨度悬索桥的节段模型风洞试验，完成了高精度高强度的节段模型风洞试验模型加工，从铝芯梁的焊接工艺和椴木板材的加工等方面对传统的节段模型加工方法进行了改进。

（2）基于Straight－forward Method的特大跨度悬索桥二维颤振性能分析方法与基于节段模型风洞试验的结果吻合良好且计算效率高，不仅验证了本分析方法的可靠性，同时也证明建造跨度为5000m的悬索桥，从空气动力稳定性的角度来说是可行的。

（3）从二维颤振的角度看，无论是中央开槽达到足够宽度的方案，还是窄开槽但设垂直及水平稳定板的组合方案都能给跨度达5000m的悬索桥提供足够高的颤振失稳与扭转发散临界风速，并能满足世界上绝大多数台风区的要求。

［1］GE Y J，XIANG H F.Aerodynamic challenges in long span bridges［C］／／Keynote paper in the Proceedings of Centenary Conference of Institution of Structural Engineering，2008：121－148.

［2］LIN T，CHOW P.Gibraltar strait crossing－a challenge to bridge and structural engineers［J］.Structural Engineering International，1991，1（2）：53－58.

［3］唐寰澄.世界著名海峡交通工程［M］.北京：中国铁道出版社，2004.

［4］KAZAMA K，YAMADA H，MIYATA T.Wind resistant design for long span suspension bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，54：65－74.

［5］CLEMENTE P，NICOLOSI G，RAITHEL A.Preliminary design of very long－span suspension bridges［J］.Engineering Structures，2000，22（12）：1699－1706.

［6］COBO DEL ARCO D，APARICIO A S.Preliminary static analysis of suspension bridges［J］.Engineering Structures，2001，23（9）：1096－1103.

［7］MATSUMOTO M，KOBAYASHIA K，NIHARA Y，et al.Flutter mechanism and its stabilization of bluff bodies［C］／／Proceeding of the 9th International Conference on Wind Engineering，New Delhi，India，1995：827－838.

［8］WILDE K，FUJINO Y，MASUKAWA J.Time domain modeling of bridge deck flutter［J］.Structural Engineering and Earthquake Engineering，1996，13：93－104.

［9］MATSUMOTO M，DAITO Y，YOSHIZUMI F，et al.Torsional flutter of bluff bodies［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，69：871－882.

［10］YANG Y Y，GE Y J，XIANG H F.Coupling effects of degrees of freedom in flutter instability of long－span bridges［C］／／Proceedings of the Second International Symposium on Advances in Wind ＆Structures，Busan，2002：625－632.

［11］SARKAR P，HONES N，SCANALAN A.System identification for estimation of flutter derivatives［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，42（1－3）：1243－1254.

邵亚会（1981－），女，河北石家庄人，博士，讲师，从事结构与桥梁抗风研究。通信地址：安徽省合肥市屯溪路193号合肥工业大学7号信箱（230009）；联系电话：18225515462；E－mail：yahuishao＠hotmail.com

Wind tunnel test on the aerodynamic stability of super－long span suspension bridge with a main span of 5000m

SHAO Ya－hui1，2，GE Yao－jun2，KE Shi－tang2，YANG Yong－xin2
（1.School of Civil Engineering，Hefei University of Technology，Hefei 230009，China；2.State Key Laboratory for Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China）

The bridge aerodynamic stability research is an urgent topic since bridge construction has entered into a new era of crossing wider sea straits.In this paper，a trial design of a 5000msuspension bridge with narrow and wide slotted steel boxes is conducted；then sectional model wind tunnel test is carried out as the first case of 5000msuspension bridge，identifying the flutter derivatives，flutter frequencies and three dynamic coefficients.Also the influence of various combination of additional stabilizers on vibration control of the narrow slotted girder are checked，finding out that the horizontal stabilizer above the narrow slotted girder can increase the critical flutter speed by 50%.Finally the Straight－forward Method for analysis of two dimensional flutter of super long span suspension bridge is proposed to check the wind tunnel results and research shows the compatibility of wind tunnel test and Straight－forward Method.Total conclusions can be drawn that both the wide slotted girder and narrow slotted girder with additional stabilizers can be feasible solutions for 5000msuspension bridge located in most of the typhoon prone areas around the world form the point of aerodynamic.

two－dimensional flutter；super－long－span suspension bridges；Straight－forward Method；aerodynamic stability；wind tunnel test

U441

A

1672－9897（2011）06－0038－07

2010－08－05；

2011－05－10

国家自然科学基金委重大研究计划重点研究项目（90715039）及中央高校基本科研业务费专项资金资助