矿区规划环境评价中灰色关联投影模型的应用

孟 帅，王翠红

（山西大学黄土高原研究所，山西 太原 030006）

1 引言

矿区规划环境评价通过以实现可持续发展为目标，对经济社会发展的科学预测评价，达到经济社会与资源环境协调发展的目的。矿区规划环评旨在从可持续发展的理念出发，针对矿区资源开发利用和环境保护中存在的主要问题，通过对矿区规划全面的分析，综合评价规划是否与矿区内的资源和环境承载力相一致，分析可能产生的环境与社会影响，提出完善规划的战略措施与对策，进一步促进资源的合理利用、产业结构与布局的优化和调整，为促进整个矿区全面、协调和可持续发展奠定科学的基础。[1～3]

文章尝试将灰色系统的理论方法引入矿区规划环境评价中，从矢量投影角度出发，提出了一种新的多指标灰色关联投影模型，并应用于晋城矿区的生态脆弱性评价中，取得了较为满意的研究成果。该方法概念清楚、涵义明确、算法简单，是一种较理想的评价方法。[4～5]

2 灰色关联投影模型的建立

矿区环境是一个复杂的大系统，涉及诸多因素，由于因素的不确定性，使得该系统成为一个灰色系统。根据矿区多维的内涵特征，采取单一的指标来度量矿区的发展水平是不够的，有必要构建一个复合指标体系来测定矿区的和谐程度。文章从矢量投影角度出发，运用灰色系统理论，建立了矿区环境规划评价的灰色关联模型。

2.1 矩阵的构造

在评价体系中评价指标与评价样本及理想样本共同组成一个样本矩阵。

以评价指标分级标准为基础，建立标准矩阵。

对评价样本进行环境质量评价的主要目的是为了通过对各个评价样本的评价指标与理想样本的距离分析，确定它隶属于环境质量标准矩阵中的哪一级。

2.2 矩阵元素的归一化

由于评价指标值量纲的不统一，因此需要对样本矩阵和标准矩阵中的元素进行归一化。这样所有的指标值都转化为0～l间的数值。

2.3 灰色关联度判断矩阵的构造

灰色关联分析的基本思想就是反映序列间的相互关联程度，在这里就是要反映各个评价样本与理想样本间的关联程度，以此作为确定评价样本隶属标准等级的依据:经过归一化后的样本矩阵，可得到子序列与母序列间的灰色关联系数，同理可以得到各级评价标准与l级评价标准间的灰色关联系数和相应的灰色关联度判断矩阵。

2.4 灰色关联投影值的计算

（1）确定各评价指标权重。由于评价指标在评价体系中所占的权重大小不同，所以必须确定各评价指标在评价体系中的权重，体现出各评价因子在评价体系中的作用大小。

（2）构造增广型加权灰色关联度判断矩阵。这样，可以对上述矩阵进行分析，进而反映出各评价样本与理想样本间的关联程度，确定其隶属的标准等级。

（3）求模的大小。模的大小可以弥补夹角余弦法的不足，但其不能反映评价样本与理想样本之间的变动方向。如果变动方向相反，模越大则样本越恶劣，因此模的大小和夹角余弦大小的结合才能全面准确反映评价样本与理想样本之间的接近程度。

（4）计算灰色关联投影值。

2.5 评价等级标准的确定

根据计算出的灰色关联投影值的大小，可以得到评价等级标准。依据投影值的大小可以得到环境质量的优劣，投影值越大，表明其与理想样本越接近，即环境质量越高，反之越低。[6～8]

3 实例分析——以山西省晋东煤炭基地晋城矿区为例

3.1 研究区域概况

晋城矿区位于山西省东南部太行山西侧，沁水煤田南端。行政区划隶属晋城市城区、陵川县、泽州县、沁水县、高平市，长治市的长子县、长治县等。地理位置介于东经 115°55″～113°36″，北纬35°12″～36°04″之间。矿区东西长为 39～117 k m，南北宽约 37～72 k m，面积约6200.7 k m2。矿区内煤炭生产的大型国有企业为晋城无烟煤矿业集团有限责任公司，现有生产矿井7对，即在老区的古书院矿、王台铺矿、凤凰山矿和新区的寺河矿、成庄矿、长平矿及北部新投产的赵庄矿。7个生产矿井核定总能力为36.30 M t/a，其中老区9.40 M t/a，新区26.90 M t/a。矿区内地方劳改及合资矿3个，设计（核定）生产能力6.50 M t/a。矿区内地方兰花集团目前下属7个生产矿井，1个在建矿井，设计生产能力共计9.60 M t/a。根据山西省煤炭资源整合和有偿使用工作领导组办公室相关文件，资源整合后矿区地方煤矿419处，采矿许可证能力共计75.84 M t/a。[9]

3.2 晋城矿区生态脆弱性评价指标体系

3.2.1 评价指标的选择

根据构建指标的全面性、独立性、科学性、动态性、可操作性等原则，结合可获取的资料，工作人员选取了4大类共12项指标，形成一个多层次的评价分析结构模型，分为自然资源指标、环境质量指标、经济发展水平指标和社会生活水平指标。如：

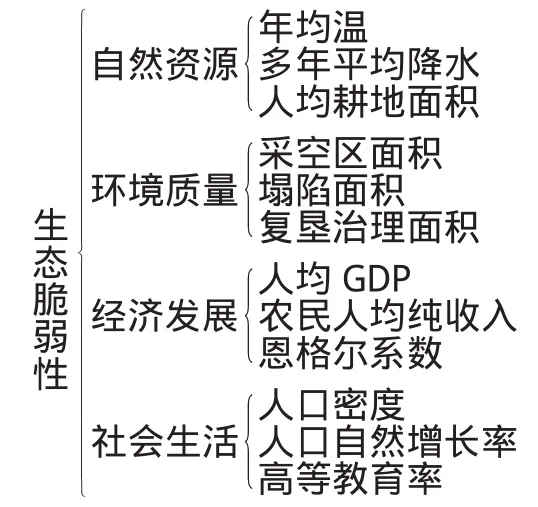
3.2.2 评价分级标准

评价分级标准的确定是矿区生态脆弱性评价十分重要的内容。遵循评价等级标准的确立原则，初步确定了晋城矿区生态脆弱性评价分级标准及现状值，见表1。

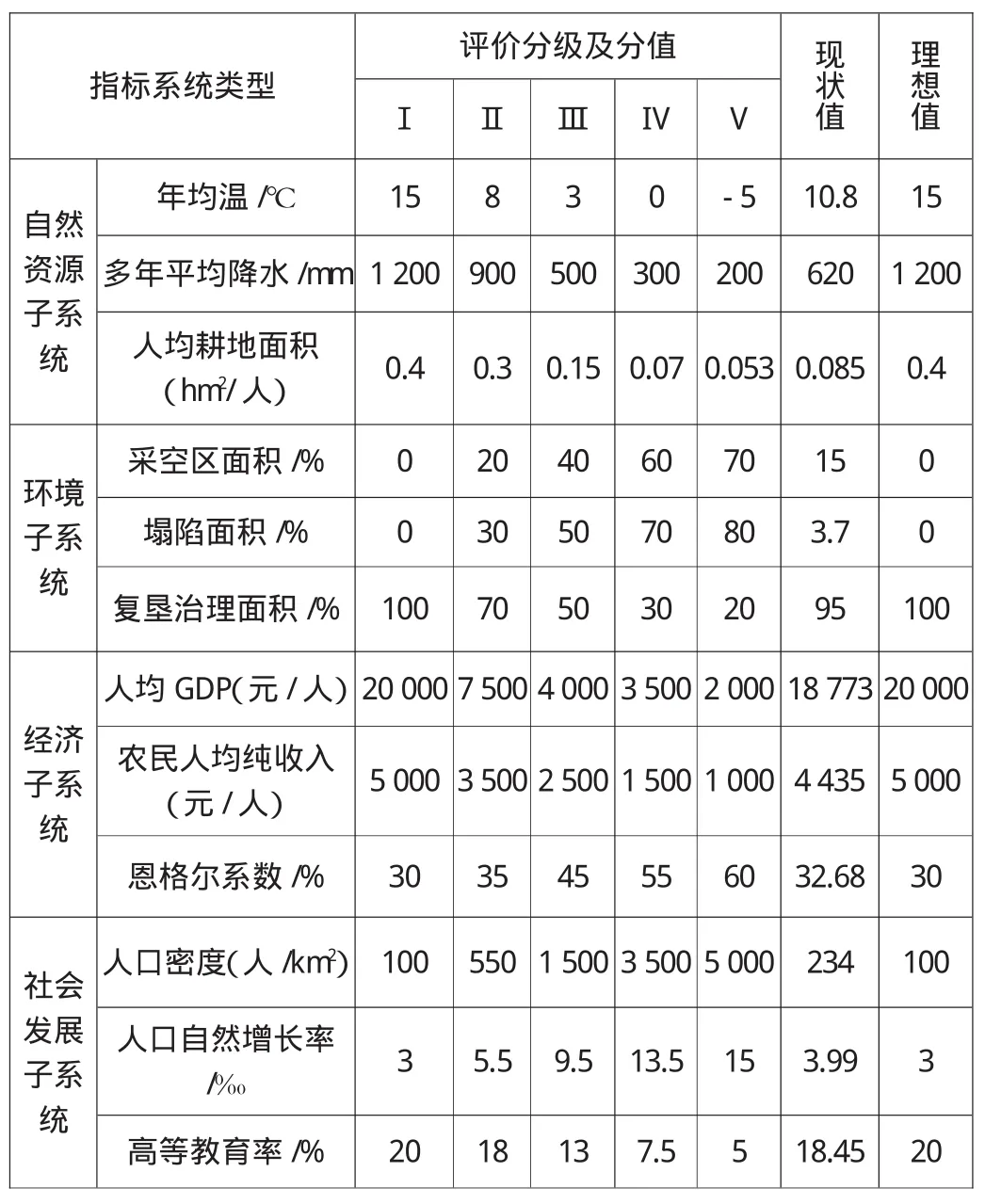
表1 评价标准及现状值

3.3 晋城矿区生态脆弱性综合评价

3.3.1 矩阵的构造及归一化

由表1可以分别建立样本矩阵X12×2和标准矩阵S12×5：

根据（1）和（2）式，分别对样本矩阵 X12×2和标准矩阵 S12×5，进行归一化处理，得到样本归一矩阵A12×2和标准归一矩阵B12×5：

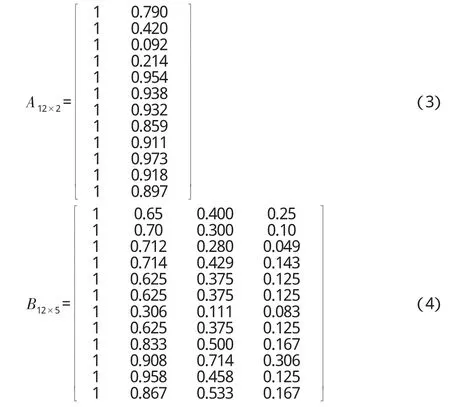
3.3.2 灰色关联度判断矩阵的构造

由（3）式可以分别计算出样本归一矩阵R12×2和标准归一矩阵 T12×5：

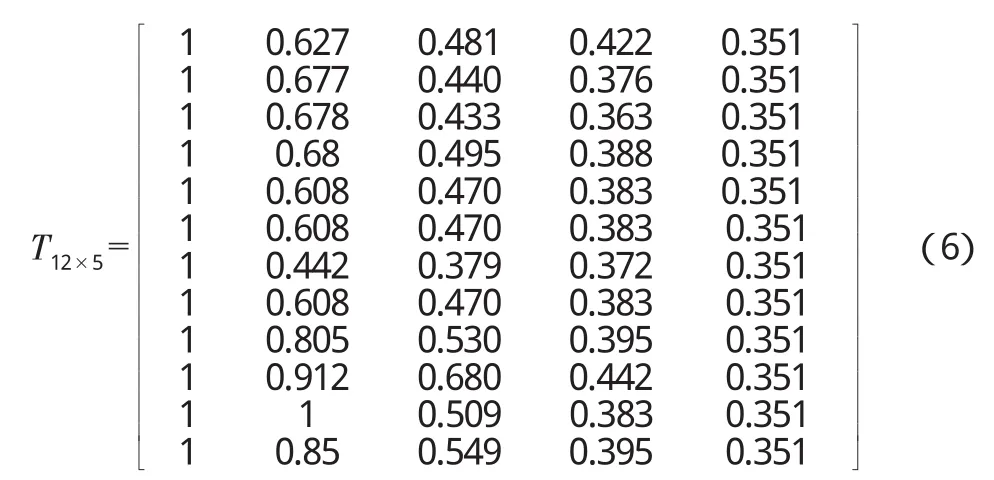
3.3.3 指标权重的确定

根据层次分析法和专家打分的方法，计算出了晋城矿区生态脆弱性各评价因子的初始权重依次为=（0.0135，0.0277，0.0234，0.04，0.068，0.0185，0.0411，0.0138，0.0061，0.0611，0.0184，0.0084）T。

3.3.4 灰色关联投影值计算

在加权向量的作用下，构造增广型加权灰色关联度判断矩阵 Z12×5和 Q12×5。

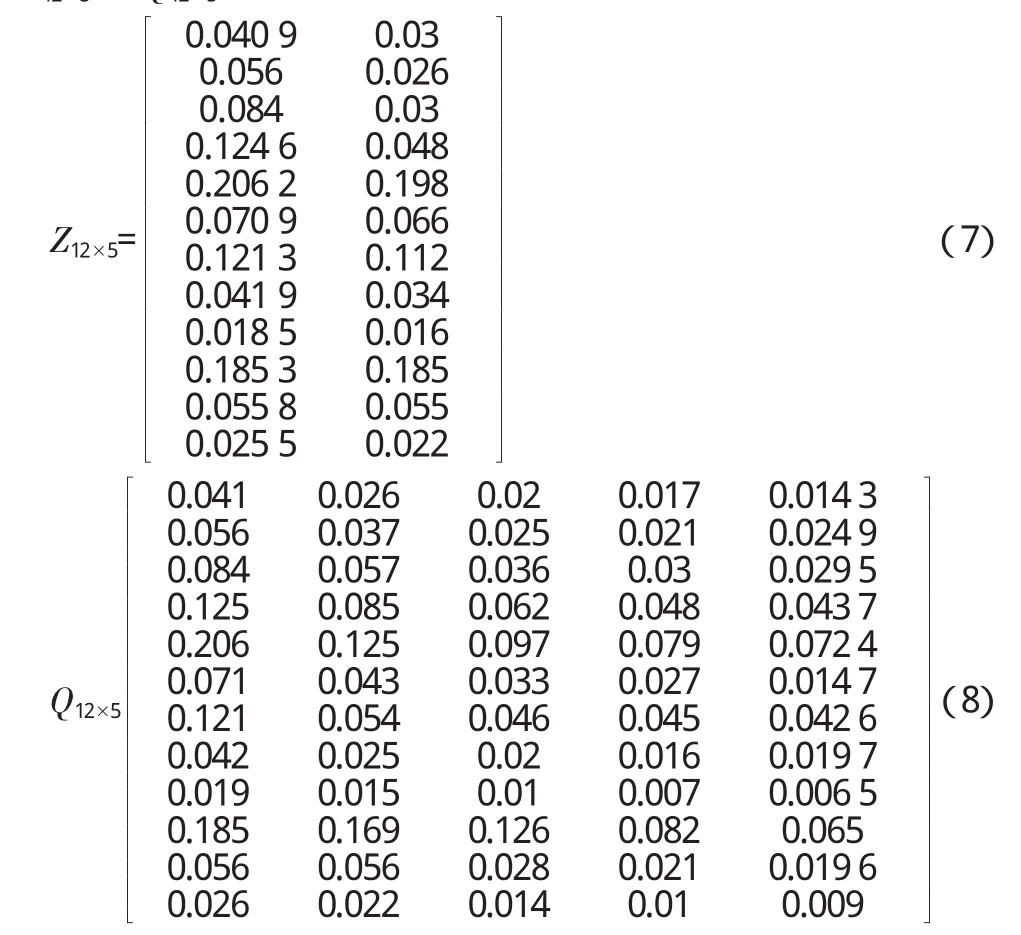
由式（5）计算得出样本的灰色投影角为c o s θ=0.9552。

然后由式（7）计算出了评价样本灰色关联投影值Y D=（理想值，现状值）=（1，0.3021）和标准矩阵灰色关联投影值 B D=（1级，2级，3级，4级，5级）=（1，0.359，0.249，0.186，0.142，0.126）；其次，根据计算出的标准矩阵灰色关联投影值及式（9）将晋城矿区生态脆弱性分为以下5个等级标准：

最后根据计算结果，目前晋城矿区生态脆弱性灰色关联投影值为YD=0.3021，根据上述的评价等级标准可以看出，目前晋城矿区生态脆弱性属3级，仅处于一般状态。矿区主要属于中度脆弱区，且该区生态环境脆弱的主要原因是不合理的耕作习惯和一些气候条件所致。因此，只要严格按计划施工，及时进行检测并采取必要的防范措施，评价区煤炭资源的开采不会对整个区域的生态构成大的威胁，并且该评价结果与实际取得了较好的一致性。

4 结束语

?在灰色关联投影模型中，评价样本与评价标准被视为多维向量，并向同一矢量进行投影，求出了各自的投影值。由于矢量投影值等于模型矢量夹角余弦两部分的乘积。因此它能更为全面、准确地反映出评价样本与理想样本两矢量间的接近程度。

在指标样本数据量少的情况下，采用灰色关联投影模型进行煤矿区环境评价，所得到的结果符合实际情况，而且与其他方法所求结果较为相近，相比其他方法有很多优点，可以简明直观的揭示引起生态脆弱性在不同区域差异的主导因素和空间分异规律,并可以为矿区规划提供理论依据等。研究结果表明，灰色关联投影模型涵义明确，计算方法简单，可操作性强,在矿区规划的环境评价中应广泛应用。

由于我国幅员辽阔，矿区的自然条件差异大，矿区的发展水平不平衡，很难用统一标准去评价差异性较大的矿区。因此，矿区规划没有绝对的评价标准，任何标准都是相对的，评价标准的选择可依据评价目的来确定。

[1]陈天乙.生态学基础教程[M].天津：南开大学出版社，1995，97—162.

[2]吴开亚，李如忠，陈晓剑.区域生态环境评价的灰色关联投影模型[J].长江流域资源与环境，2003，12（5）：473-478.

[3]邓聚龙.灰色系统基本方法[M].武汉：华中工业学院出版杜，1987.

[4]汤亚林，韩家悦，门宝辉.水利项目投资决策的灰色关联投影模型及其应用[J].南水北调与水利科技，2005，3(1)：30-32.

[5]李仕兵，赵定涛.区域环境友好度评价的灰色关联投影模型及应用.科学学与科学技术管理，2007，8：114-117.

[6]贺瑞军.关于煤炭矿区规划环评思路及重点的思考[J].山西煤炭管理干部学院学报，2009.

[7]杨风等.大型煤炭矿区规划环境影响评价中的循环经济分析[J].干旱区资源与环境，2010，24（4）：32-37.

[8]曹伟，盛煜.煤矿区冻土环境评价的灰色关联投影模型.水文地质工程地质，2008，4：111-115.

[9]北京华宇工程有限公司.山西晋东煤炭基地晋城矿区总体规划环境影响报告书.2009，11.