流体力学的原理在煤矿通风系统中的应用

王 飞

（山西太原东山煤矿有限责任公司，山西 太原 030043）

1 引言

由于煤矿工作场合的特殊性，需要对井下各工作地点创造良好的通风环境，有足够的新鲜空气，使其中有毒、有害、有爆炸性的气体、粉尘不超过规定值，使气温适宜。煤矿井下巷道风流运动过程中，由于巷道两帮条件的变化，均匀流在局部地区受到局部阻力物（如巷道断面突然变化、风流分叉与交汇、巷道转弯等）的影响而破坏，引起风流流速的大小、方向或分布的变化，产生涡漩等，造成风流的能量损失，同时又有可能引起瓦斯等有害气体的积聚，从而给安全带来隐患。

2 风流流动状态

风流在同一巷道中，因流速的不同，形成质不同的流动状态。通过实验表明，流体在直巷内流动时，在一般情况下，当Re≤2000～2300时，流体状态为层流，当Re＞4000时，流动状态为紊流，在Re=2000～4000的区域内，可能是层流，也可能是紊流，随着巷道的粗糙程度，风流根据进入巷道的情况等外部条件而定。而层流流动时，只存在由黏性引起的各流层间的滑动摩擦力；紊流流动时，则有大小不同的涡体动荡于各流层之间，除了黏性阻力外，还存在由于质点掺混、互相碰撞所造成的惯性阻力。

巷道风流流态与巷道平均风速、断面及巷道周界长有关，具体表示为：

Re=4 vS/Uυ

式中：S：井巷断面 m2；

U：井巷周界长 U≈c S1/2，m；

v：井巷平均风速，m/s；

υ：空气的运动黏性系数，通常取15×10-6m2/s；

c：断面形状系数；

梯形断面，c=4.16；

半圆拱断面，c=3.90。

根据此公式可以计算出风流在巷道中的流动状态。

3 巷道通风阻力原理

3.1 局部阻力

风流在运动过程中，由于巷道边凸凹不平的变化，均匀的风流受到局部阻力而影响破坏，引起风流流速大小、方向的变化，产生漩涡等。局部阻力的成因和摩擦阻力类似，局部阻力hl一般用动压的倍数来表示：

hl=ξρ/2 ν2

式中：ξ：局部阻力系数。

试验表明，在层流条件下，流体经过局部阻力物后仍然保持层流，则局部阻力还是由流层之间的黏性切应力引起的，只是由于巷道两边的变化，使流速重新分布，加强了相邻流层间的相对运动，而增加了局部能量损失。此时，局部阻力系数ζ与Re成反比，即：

ξ=B/Re

式中：B：因局部阻力物形式不同而异的常数。说明层流的局部阻力也是和平均流速ν的次方成正比。

为了探讨局部阻力的成因，分析几种典型局部阻力物附近的流动情况。

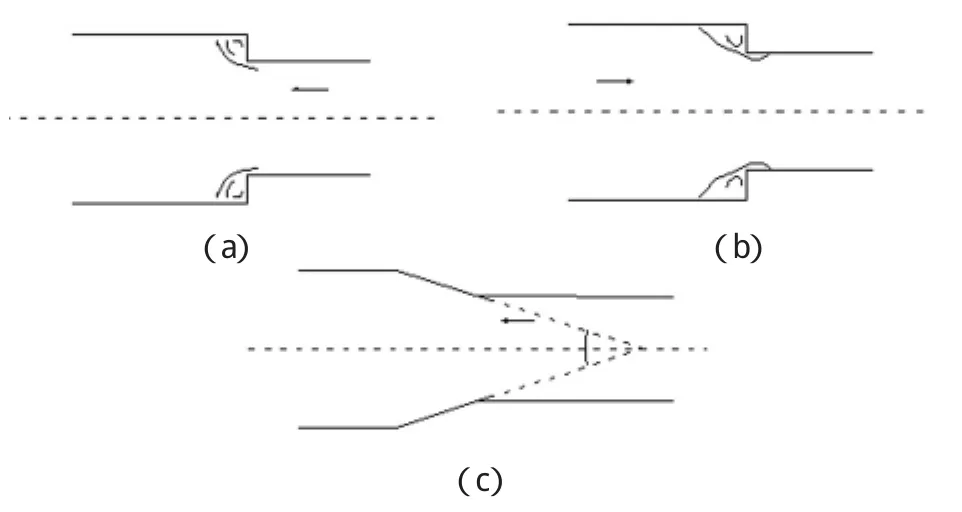
图1

如图1所示，紊流流体通过突变部位时，由于惯性力的作用，不能随从边壁突然转折，出现主流与边壁脱离的现象，在主流与边壁之间形成涡漩区，产生大尺度涡漩，不断地被主流带走，补充进的流体，又形成新的涡漩，因而增加了能量损失。

风流经过转弯处流体质点受到离心力的作用，在外侧形成减速增压区，也能出现涡漩。过了转弯处，如流速较大且转弯曲率半径较小，则由于惯性作用，在内侧又出现涡漩区，它的大小和强度都比外侧的涡漩区大，是能量损失的主要部分。

由上讨论可知，局部的能量损失主要和涡漩区的存在有关系，涡漩区愈大，能量损失愈多。仅仅流速分布的改变，能量损失是不会太大的。在涡漩附近，主流的速度梯度增大，也增加能量损失，在涡漩被不断带走和扩散的过程中，使下游一定范围内的紊流脉动加剧，增加了能量损失，这段长度称为局部阻力物的影响长度，在它以后，流速分布和紊流脉动才恢复到均匀流动的正常状态。

大量实验研究表明，紊流局部阻力系数ξ一般取决于局部阻力物的形状、边壁的粗糙程度，前者是主要影响因素，后者在粗糙程度较大的支架苍道中也需要考虑。

下面分别讨论各种形式局部阻力的计算方法。

3.1.1 突然扩大

如图1（a），突然扩大时的局部阻力计算公式可用能量方程和动量方程从理论上推导出来，即水力学中的包达一卡诺公式:

H l e x p=ρm（ν1-ν2）2/2

式中：ν1：小断面的平均流速；ν2：大断面的平均流速；ρm：空气平均密度。

该式的导出条件是两断面间的摩擦阻力损失忽略不计。

对于粗糙程度较大的矿井巷道，可按巷道的摩擦阻力系数α值（用工程单位制数值），对ξ值予以修正。

修正后局部阻力系数ξ′e x p用下式计算：

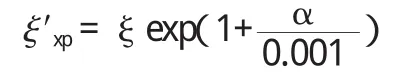
3.1.2 突然缩小

如图1（b），突然缩小时的能量损失大部分发生在由于惯性而形成的收缩断面以后的流道上，主要是该断面附近的涡漩区造成的。突然缩小的局部阻力系数ξshr取决于巷道收缩面积比，对应于小断面的动压 ρ/2 ν2，ξshr可按下式计算：

ξshr=0.5（1-S2/S1）

考虑巷道粗糙程度的影响，突然缩小的局部阻力系数ξ′shr可用下式计算：

ξ/s h r=ξs h （r1+α/0.0013）

式中α用工程单位制数值k g f.s2/m4。

3.1.3 逐渐扩大

如图1（c），逐渐扩大的局部阻力比突然扩大小得多，其能量损失可认为由摩擦损失和扩张损失两部分组成，后者是涡漩区和流速分布改变所形成的损失。当断面比n（等于S2/S1）一定时，渐扩段的摩擦损失随扩张角θ增大而减少，而扩张损失却随θ增大而增大。θ在5°～8°范围内，渐扩段的能量损失最小。矿井主扇风机作抽出式工作时，为了减少风机出口动能的损失（也可看做突然扩大到大气的一种局部阻力），必须安设扩散器，扩散器的扩张角一般不超过8°～10°。

在扩张角θ小于20°时，渐扩段的局部阻力系数ξgex可用下式求算：

ξl e x=α（/ρs i n θ/2）×（1-1/n 2）+s i n θ（1-1/n）2

式中：α：风道的摩擦阻力系数，k g/m3；

θ：扩张角。

3.2 摩擦阻力

由于流动状态的不同，摩擦阻力与流速的关系有不同的规律。而矿井支护形式是多种多样的，断面有大小，支架规格不同，巷道的相对粗糙度差别很大。尤其棚架巷道在巷道壁附近容易产生强烈的涡漩和扰动，造成很大的损失。

巷道摩擦阻力与巷道粗糙程度、断面、周长、空气密度等有关系，具体为：

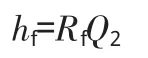
式中：Rf：巷道的摩擦风阻 Rf=αLU/S3；

例：本矿观家峪进风井，全长L=2000 m，巷道断面S=8m2，采用工字钢棚架支护，支架纵口径△=6，通过风量Q=50m3/s空气平均密度 ρm=1.25 k g/m3。（见图 2、图 3，α 取 0.0177 k g/m3）具体得：

梯形断面周长U≈cS1/2=4.16×81/2=11.77 m

巷道摩擦风阻Rf=αLU/S3=（.0177×2000×11.77）/83=0.815 k g/m3

巷道摩擦阻力hf=RfQ2=0.814×502=2035 P a

经过半年的喷浆整修，使巷道增加了光滑度，减小摩擦阻力（α 取 0.00417 k g/m3）。

具体得：梯形断面周长U≈cS1/2=3.85×81/2=10.89 m

巷道摩擦阻力 hf=RfQ2=（0.00417×2000×10.89）/83×502=443 P a

采用喷浆巷道支护，可以有效地减小摩擦阻力，降低风量的损耗。所以，对于进风巷道，选择合理的支护形式有很大的经济意义。

图2 棚架支护巷道

图3 喷浆后巷道

4 结束语

通过对以上几种典型局部阻力分析，在矿井巷道通风过程中，为减少局部风阻，应尽量避免井巷断面的突然变化；断面大小悬殊的井巷，其连接处断面应逐渐变化；尽量避免井巷直角转弯或大于90°的转弯，转弯处内外侧要做成圆弧形，有一定的曲率半径；在选用支护材料时，尽量采用相对粗糙度小的支护方式，从而可有效降低风流在巷道中产生的涡漩和扰动。