GPS 高程异常拟合方法研究

贾自甜 何 浩

众所周知，GPS技术已经被广泛应用到各个领域，如环境检测部门的数据采集、地理信息系统的建立、地质灾害的预报、监测等。GPS的高精度，全球性，全天候等特点已被大家所共识，为提高经济效益，减少外业工作量，人们广泛采用GPS定位技术进行平面定位。但GPS测高数据的应用却没有像GPS平面成果那样被广泛应用。这主要是因为GPS所测的高程为大地高程。由于大地高程面和水准面不平行，产生了高程异常现象。因此GPS高程只有经过高程异常的改正才能应用到工程测量和城建系统中。大地水准面是一个不规则的曲面，它不可能完全通过一个数学模型来精确的描述。如何利用GPS所测的大地高，通过某种算法求出该点的正常高，一直是GPS测量研究的热点。

1 拟合方法

GPS测得的大地高表现为WGS-84参考椭球面沿该点的法线方向，正常高表现为该点的铅垂方向，这两方向的偏差即为垂线偏差。但由此引起的高程异常一般不超过±0.1 mm，完全可以忽略。由于考虑到垂线偏差对高程转换的影响比较微弱和工程测量作业范围内高程异常的相对恒定性，因而，在计算时没有必要专门来考虑垂线偏差，而是将其直接参与到多项式求解过程当中。确定高程异常的方法有:

1)在局域范围，基准站和流动站的距离不超过5 km，且测区范围内的地形起伏变化不大时，可认为测区内各点的高程异常值是相同的。如测区内A，B两点，其大地高和正常高分别为:HA，HB，hA，hB，其中，A 为已知点，则 A 点的高程异常为:

基于以上假设，则B点的高程异常为:

此时，已知B点的大地高，则可求出其正常高:

2)若测区内地形起伏较大，且基准站和流动站距离较大时，通常确定高程异常的方法有直接法和几何法两种。a.直接法。直接法又称为重力法。重力法就是利用流动站附近的重力测量资料求解大地水准面的非线性变形部分的高程异常值。高程异常是地球重力场的一个参数，一般情况下，利用地球重力场模型，根据点位信息，即可求出该点的高程异常。对高程精度要求不高或不可能进行水准测量的困难地区，可采用直接法。b.几何法。几何法又称为解析法。解析法就是用一个一次或高次的多项式来拟合出似大地水准面模型，即高程异常模型，从而内插出某点的高程异常值。根据测区的情况可将似大地水准面用多项式曲线、平面和多项式曲面来表示，对应的就有多项式曲线拟合、平面拟合和多项式曲面拟合三种方法。

多项式曲线拟合法:当GPS点呈线状布设，可根据控制点的平面坐标x(或y)及其高程异常，通过构造一个插值函数来拟合测线方向上的大地水准面曲线，然后内插出高程异常值。

选用一个m次代数多项式作为插值函数，设高程控制点的高程异常为:

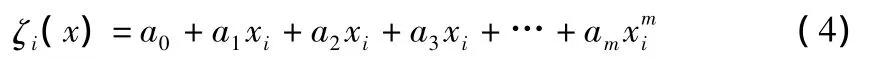
各高程控制点的高程异常值与拟合值之差为:

其中，ri为拟合误差。根据最小二乘原理求出ai(i=0，1，…，m)的值，代入式(4)则可用于求解高程异常。

插值多项式的次数m并非越高越好，会出现不收敛的现象(Runge现象)。

平面拟合法:对于范围较小的平坦或低丘地区，似大地水准面可看成平面。设测区内高程控制点的平面坐标为(xi，yi)，此时，选用插值函数为:

其中，εi为拟合误差。根据最小二乘原理求出ai(i=0，1，2)的值，代入式(6)即可求得平面拟合模型。

多项式曲面拟合法:对于范围稍大的地区应把似大地水准面看成是多项式曲面。当测区似大地水准面起伏较大，且重合点数较多时，可采用曲面拟合来逼近似大地水准面。设测区内高程控制点的平面坐标为(xi，yi)，选用的插值函数为:

同样，根据最小二乘原理求出待定系数ai的值，代入式(7)即可求得多项式曲面拟合模型。

2 拟合精度估算

GPS拟合高程精度一般采用的计算方法是:计算拟合点的拟合中误差，分析GPS拟合高程的内符合精度;联测若干已知几何水准高程的GPS网点作为检核点，计算检核点的拟合中误差，分析GPS拟合高程的外符合精度;将检核点的高程异常与拟合的高程异常差，同相应等级的水准测量限差进行比较，分析GPS拟合所能达到的精度。

内符合精度为:

其中，εi为参加拟合点的拟合残差;n为拟合点数。

外符合精度为:

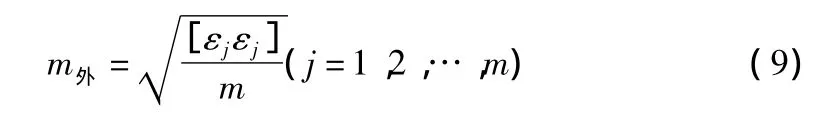
其中，εj为检核点的高程异常与拟合的高程异常之差;m为检核点的个数。

对于四等水准:

其中，L为检核点到最近拟合点的距离，km。将εj的值与ε限进行比较即可判断出每个检核点的εj是否超限。

3 结语

在我国范围内，高程异常误差对坐标的影响随经度减小而增大。在我国的西部边缘区域，1 m高程异常误差对平面坐标的影响达数厘米，而此区域的高程异常误差通常达2 m～3 m，按照坐标误差与高程异常误差成正比的关系，则对转换后的坐标影响达数分米，因此必须给予重视。

由于我国西部地区平均海拔高度较高，高程异常精度较差，经度值较小(87°～96°)，因此，不能采用利用正常高加高程异常值求大地高，再由空间公共已知点求转换参数，实现坐标转换的方法。而在东部地区，平均海拔低，经度值较大(119°)，高程异常精度较好(±0.5 m)，因此，在一些精度要求不是很高的情况下，可采用此方式进行坐标转换，再将转换后的坐标投影到平面，实现WGS-84坐标向国家或地方平面坐标的转换。

[1]张 勤，李家权.GPS测量原理及应用[M].北京:科学出版社，2005.

[2]张 勤，王 利.GPS坐标转换中高程异常误差影响规律研究[J].测绘通报，2001(6):21-22.

[3]姜晨光，盖玉松.我国GPS高程异常的调查与分析[J].勘查科学技术，2003(1):37-38.