基于改进的监督LLE人脸识别算法

李白燕，李 平，陈庆虎

(1.黄淮学院信息工程系，河南 驻马店 463000;2.武汉大学电子信息学院，湖北 武汉 430079)

0 引言

人脸识别仍是现阶段模式识别和计算机视觉领域的研究热点之一［1］，由于人脸图像受光照、姿态、表情等影响，人脸数据是异常高维的数据。目前对高维数据的处理，有两种基本方法:一种是将高维数据映射到线性可分的高维空间中，即基于内核的技术，如支持向量机(SVM)技术［2］;另一种方法是降低数据维数，虽然看似信息丢失，需要估计的参数减少，但可能会有更好的识别性能。许多线性降维方法，如主成分分析(PCA)［3］和Fisher线性判别分析(LDA)［4］是行之有效的。但是大量研究表明，人脸空间更可能是一个高维的非线性子空间，即人脸位于一个非线性流形上，因此线性降维方法不能反映人脸的非线性数据结构，不足以描述人脸特征。目前流形学习可分为全局映射和局部映射两类。前者主要有等距映射(isomap)［5］;后者有局部线性嵌入(Locally Linear Embedding，LLE)［6］和拉普拉斯特征映射(Laplacian Eigenmaps)［7］。但是这些方法都没有明晰的投影矩阵，从而不能直接映射新的测试点(该点不同于训练集合中的任何点)，这个问题也被称为 out－of－sample 问题［8］。其中 LLE 有很多优点:不需要一个迭代算法，很少的参数需要进行设置，而且该方法避免了局部极小问题，具有邻域保持特性。但是该算法会出现上述所说的问题，而且属于基于重构的无监督的学习方法，效果并非最优。因此，Dick de Ridder等在LLE学习算法的基础上引入监督机制，称为SLLE［9］，SLLE是以监督的方式提取人脸的非线性的流形特征，该算法分类性能优于LLE，通常情况下也会优于其他的一些映射算法，庞等人在LLE基础上，提出了一种新的基于核子空间的学习方法，即核邻域保持投影(KNPP)［10］。该方法引入一个线性变换矩阵来近似LLE，然后通过非线性核技巧在维数很高的空间里求解子空间，它可以解决 out－of－sample问题。KNPP最大的优点在于它和LLE一样具有邻域保持特性，但是KNPP属于无监督学习方法，需要发展为有监督的方法。因此，在SLLE与KNPP算法的启发下，本文提出一种新方法，简称为IM_SLLE。

1 LLE，SLLE和KNPP概述

1.1 局部线性嵌入LLE

给定 N 个输入向量 X=［X1，X2，…，XN］，其中，Xi∈RD，通过 LLE 算法将得到输出值 Y=［Y1，Y2，…，YN］，Yi∈Rd且d≪D。无监督LLE归结为3步［6］:

1)在高维空间中寻找每个样本点Xi的K个近邻点;

2)由每个样本点的近邻点计算出该样本点的局部重建权值矩阵;

3)由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值Yi。

1.2 监督局部线性嵌入SLLE

SLLE的主要目的是找到将类间结构和类内结构分开的映射，其方法是在Xi和Xj(属于不同类)加上一个距离参数，修改K个近邻点的计算方法，从而增加了样本点的类别信息。而步骤2)和步骤3)同LLE。SLLE在计算点与点之间的距离采用如下公式［9］

式中:Δ是没有考虑类别信息的欧式距离，Δ'是结合了类别信息的距离，Λij取值为0或1，当两点属于同类时，取为0，否则取1;α 是控制点集之间的距离参数，α∈［0，1］，α是一个经验参数。当取为0时，此时的SLLE和LLE算法相同。

1.3 核邻域保持投影KNPP［10］

给定 N 个输入向量 X=［X1，X2，…，XN］，其中，Xi∈RD，假设通过非线性映射函数Φ:X→Φ(X)把X映射到Hilbert空间F中。KNPP的目的是对F中的数据点Φ(X)=［Φ(X1)，Φ(X2)，…，Φ(XN)］降维，把它们映射为d维空间中的新的数据点X=［Y1，Y2，…YN］，其中 d≪D。

1)求出距离每个数据点Φ(xi)最近的k个点，距离可以通过核矩阵K来计算，核矩阵K的元素为Kij=Φ(Xi)·Φ(Xj)。

2)通过求解式(2)所示的最小二乘问题，计算Xi到它的邻域点之间的最佳重建权重Wij

3)分解核矩阵K并计算矩阵M和Q。K=PΛPT，M=(I－W)(I－W)T，Q=PTMP，其中 I表示单位矩阵。

4)求解下面的特征值分解问题得到向量ri:Qli=liri，其中0＜l1＜… ＜ld。

5)计算向量 βi并对其归一化 βi=PΛ－1ri，βi←βi/，其中 i=1，2，…，d。

6)采用yin=βnjKji实现非线性降维其中n=1，2，…，d。yin表示向量yi的第n个元素。

2 改进的算法IM_SLLE

下面结合SLLE和KNPP算法，提出改进算法，步骤如下:

1)计算每个样本点的K个近邻点

在SLLE算法中，式(1)中的Δ采样欧氏距离得到，在本算法中通过核矩阵K来计算，K的元素为Kij=Φ(Xi)·Φ(Xj)，其中Φ是引入的非线性映射函数。然后在根据式(1)计算Δ'从而找到K个近邻点，计算方法中已经加入了样本点的类别信息，不过可将式(1)进一步进行改进。一个理想的分类机制应最大类间差异而最小化类内差异［11］，因此将SLLE中的式(1)通过减少类内距离而扩展类间距离，得到

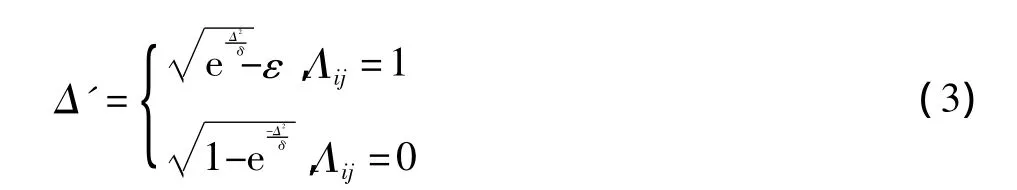
式中:Δ通过核矩阵K计算得到的Xi和Xj之间的距离，参数δ防止当Δ较大时，Δ'按指数增长太快，因此δ与样本点的紧密度有关，常数ε在［0，1］之间取值，合理的取值可使不同类之间的数据更相似，以至使类间差异可能比类内差异更小。

下面分析一下改进后的特点。图1a是采用式(1)计算的Δ'欧氏距离从0～3线性变化，ε设为0.2。水平轴代表欧式距离Δ，纵轴代表Δ'，实线表示不同类之间距离的变化，虚线表示同类间距离的变化。从图1可以看出，在SLLE中，类间差异会随着类内差异的线性增加而增加，将不利于随后的分类识别。因为类间与类内的距离比值是不变化的，这样使嵌入数据的判别能力和泛化的能力被限制在一定的范围。另外，SLLE对数据中的噪声也是非常敏感的，具体来说，类间距离和类内距离的范围都是［0，+∞］，这意味着噪声可能会改变原始的差异到中间的任何值，特别是当噪声比较强时，数据间的邻域关系可能被完全破坏。

采用式(3)所计算出的Δ'如图1b所示，这里水平轴代表核矩阵K距离Δ，其他同图1a，从图中可以看出，随着距离Δ的增加，类间差异比类内差异大，因此类间距离与类内距离的比值变得越来越大，这样克服了SLLE存在的问题，有利于分类识别。另外，当距离Δ增加时，类间差异增加快而类内差异增加慢，这表明这种算法对数据中的噪声有抑制的能力。一方面，类间距离通常是比较大的，所以如果它越小，噪声存在的可能性就越大，Δ'减小得越慢。另一方面，类间距离通常是比较小的，如果它越大，噪声存在的可能性就越大，Δ'增长得越慢。因此，随着噪声存在的可能性增加，改进算法抑制噪声的能力也逐步加强。

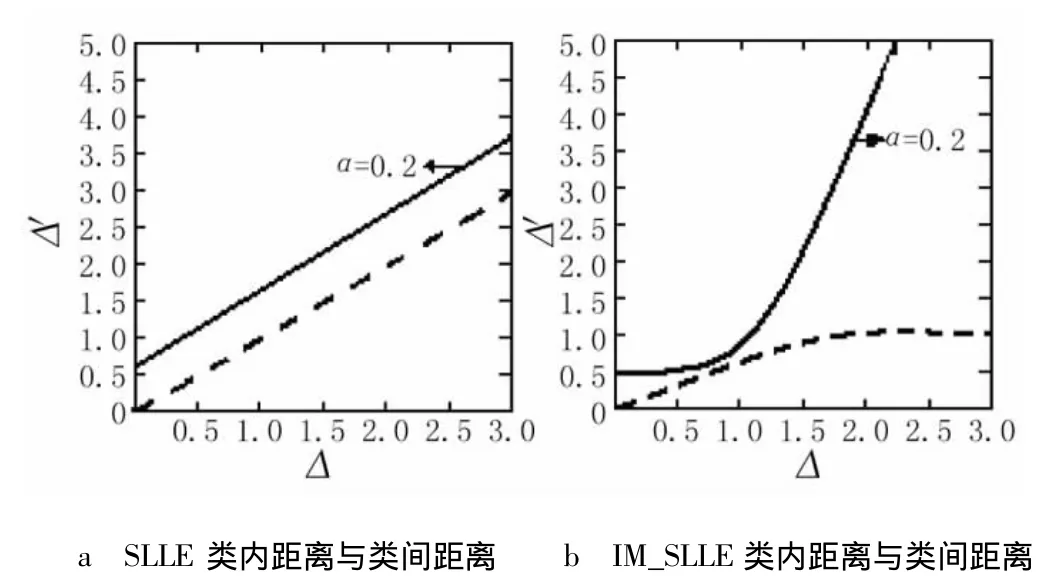
图1 SLLE与IM_SLLE距离比较

类间差异的范围在［1－ε，+∞］，而类内差异的范围是［0，1］，因此不管数据中的噪声是多么强大，类间差异和类内差异能被控制在一定的范围，这就表明该算法能限制噪声的影响。

2)计算样本点的局部重建权值矩阵Wij

传统的LLE算法是首先定义一个误差函数并最小化［6，11］，如式(4)所示

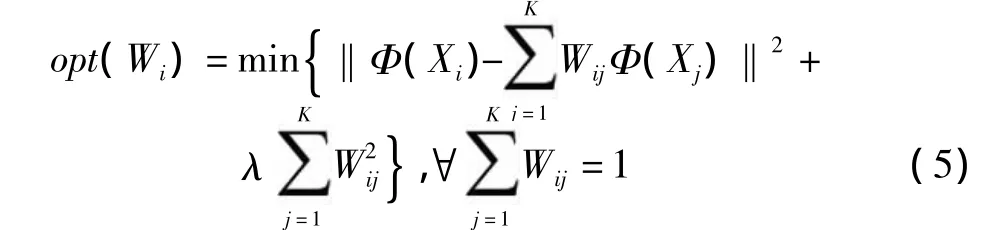
通过式(5)可求出 Wi(i=1，2，…，N)，其他步骤同1.3节KNPP的步骤，在这里不再赘述。

3 实验结果

采用Yale人脸库对文中所提出的改进算法上进行评测。Yale人脸库包含15个人的165个灰度图像，这些图像是在不同的光照、不同表情下取得的，还分戴眼镜和不戴眼镜两种情况。如图2所示。随机选取了30幅图像(每人2幅)作为识别测试集，剩下的135幅作为训练集。首先将图像裁剪和缩放为60×60的标准。

图2 样本图片

实验中将改进算法与LLE算法、SLLE算法以及KNPP算法进行比对，分类方法都采用最近邻分类器，同时对所有的算法都采用最佳的参数，实验结果如表1所示。另外为了验证非线性算法比线性算法能更好地描述人脸的流形结构，实验增加了对LDA识别率的比对。

表1 在Yale中几种算法在相应的维数下识别率比较

实验结果表明，线性算法LDA对人脸识别弱于其他非线性算法，因为非线性算法提取的特征对人脸流形的描述更加细致。在非线性人脸识别算法中，LLE算法具有邻域保持特性，但由于缺乏类别信息，效果很难达到最优。KNPP属于无监督的子空间学习方法，因为KNPP具有邻域保持特性，而且它通过利用局部信息来描述人脸的非线性流形，效果优于LLE。改进算法结合了KNPP与SLLE的优点，属于有监督的局部保持的非线性子空间学习方法，优于其他几种。这表明IM_SLLE更利用分类识别。

接下来，在预处理好的人脸图像中不同程度的加入噪声，来验证IM_SLLE算法对噪声的抑制能力，结果如表2所示，该结果是在最优参数下得到的。从表2可以看出，在不同程度的噪声下，IM_SLLE都有优于SLLE算法识别率。

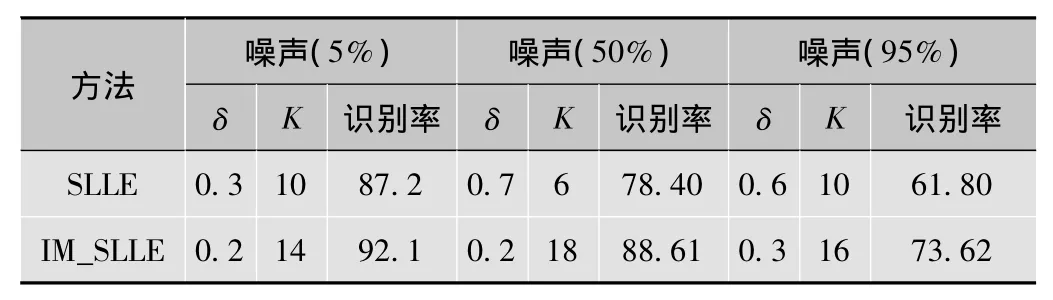
表2 SLLE与IM_SLLE抗噪能力比较

4 小结

本文针对LLE，SLLE和KNPP算法各自的有缺点，提出了一种改进算法I－SLLE，该算法在LLE的基础上引入有监督的学习机制，利用δ和ε参数加入样本的类别信息，通过最小化局部数据的全局重构误差，结合核邻域保持投影，提取高维人脸数据的非线性特征。在人脸库Yale中比较了改进算法和其他的人脸识别算法，该算法有较好的识别性能。

［1］闫娟，程武山，孙鑫.人脸识别的技术研究与发展概况［J］.电视技术，2006，30(12):81－84.

［2］BURGES C.A tutorial on support vector machines for pattern recognition［EB/OL］.［2010－12－15］.http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.122.3829＆rep=rep1＆type=pdf.

［3］TURK M，PENTALND A.Eigenfaces for recognition［EB/OL］.［2010－12－15］.http://www.face－rec.org/algorithms/PCA/jcn.pdf.

［4］BELHUMEUR P，HESPANHA J，KRIENGMAN D.Eigenfaces vs.fisherfaces:recognition using class specific linear projecttions［EB/OL］.［2010－12－15］.http://cs.gmu.edu/～kosecka/cs803/pami97.pdf.

［5］TENENBAUM J B，SILVA V，LANGFORD J C，et al.A global geometric framework for nonlinear dimensionality reduction［EB/OL］.［2010－12－15］. http://citeseerx.ist.psu.edu/viewdoc/download? doi =10.1.1.110.6050＆rep=rep1＆type=pdf.

［6］ROWEIS S，SAUL L.Nonlinear dimensionality reduction by locally linear embedding［EB/OL］.［2010－12－15］.http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.12.7171＆rep=rep1＆type=pdf.

［7］BELKIN M，NIYOGI P.Laplacian eigenmaps for dimensionality reduction and data representation［EB/OL］.［2010－12－15］. http://cseweb.ucsd.edu/～saul/teaching/cse291s07/laplacian.pdf.

［8］BENGIO Y，PALEMENT J，VINCENT P，et al.Out of sample extensions for LLE，isomap，MDS，eigenmaps，and spectral clustering［EB/OL］.［2010－12－15］.http://www.iro.umontreal.ca/～lisa/pointeurs/tr1238.pdf.

［9］DERIDDER D，KOUROPTEVA O，OKUN O，et al.Supervised locally linear embedding［EB/OL］.［2010－12－15］.http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.5.6218＆rep=rep1＆type=pdf.

［10］庞彦伟，俞能海，沈道义，等.基于核邻域保持投影的人脸识别［J］.电子学报，2006，34(8):1522－1524.

［11］陈高曙，曾庆宁.基于LLE算法的人脸识别方法［J］.计算机应用研究，2007，24(10):176－177.