对含脉冲噪声的图像去噪算法的研究

张必武，冯穗力

(华南理工大学电子与信息学院，广东 广州 510640)

0 引言

在多媒体图像传输过程中虽然采用了纠错编码技术来增强数据传输的可靠性和准确性，但是无线通信的衰落信道环境恶劣，而信道编码的纠错能力总是有限的，可能导致部分出错的图像数据难以纠正，其原因是引入了一种脉冲噪声。脉冲噪声一般由随机值脉冲噪声和椒盐脉冲噪声构成。

图像去噪是寻找一种向原始的真实信号最优逼近的算法，最大可能地分离真实信号和噪声信号，进而保留真实信号和去除噪声信号。在空间域一般采用非线性滤波技术如中值滤波来去除脉冲噪声。由于人的视觉具有主观性，在本质上是一个模糊系统，用模糊模型对图像进行去噪，能更好地保护图像边缘和细节，提高信噪比［1－2］。

在图像去噪时，首先要建立合理的噪声模型，然后选择和设计合适的去噪算法。文献［3］的噪声模型为椒盐噪声，而真实场景的脉冲噪声值一般由多个随机值构成。文献［4］中的梯形隶属函数模型的分界点不易确定，设定分界点的值势必增加运算的复杂度，实时性和可行性较差。文献［5－6］建立了较为切合实际的脉冲噪声模型。本文提出的两种算法主要与文献［6］进行了比较和分析。

本文结合无线通信中引入噪声的特点建立含脉冲噪声的图像模型如下

式中:g(i，j)表示含脉冲噪声的图像;f(i，j)表示原始图像;n(i，j)表示脉冲噪声。n(i，j)是由幅度增量在［－Am，Am］范围内的随机值脉冲噪声和一定密度的椒盐噪声的组合。本文采用的模糊聚类去噪算法在运算复杂度和去噪性能上进行了较好的权衡，具有较好的去噪效果和实时性，同时算法实现简单易行。

1 基于聚类算法的去噪方法

在含脉冲噪声的图像中，图像信号和噪声是相互独立的，像素的灰度值不满足齐次性和叠加性，一幅图像可以看作为非线性系统。本文采用聚类算法对非线性系统进行噪声消除的思想对含脉冲噪声的图像进行去噪。聚类算法的核心问题是寻找聚类中心来代替子窗中心像素的灰度值，用以向真实信号的逼近。设聚类中心Omn，中心像素 Imn。Iij∈Ω5×5，Ω5×5为5 ×5 滑动子窗，则由聚类算法得到表达式为

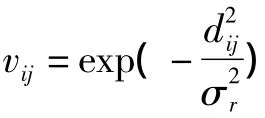
1.1 基于硬聚类模型的去噪算法(算法1)

硬聚类将集合进行非此即彼的绝对化二值逻辑划分，这种分类把具体的元素通过严格的界限区分开来，每个具体元素都只属于一个聚类;并且明确地定义共同属性，使集合中的所有元素平等享有共同属性。基于硬聚类模型的去噪算法步骤如下:

通过以上4步即可得到去噪后的图像。硬聚类的隶属函数uA的取值集合为{0，1}，它只能表示确定性概念。虽然硬聚类去噪算法运算量较小，实时性较好;但是如果子窗的噪声点与信号的灰度差分远大于噪声方差时，硬聚类算法中的隶属度只能取0或1，可能使得真实的信号的权值系数置0，从而聚类中心的迭代调整只能在噪声点中进行，以致不能去除个别的噪声点。所以下面采用基于模糊模型的去噪算法进行图像去噪，能够更好地进行迭代调整聚类中心来逼近原始信号，提高信噪比。

1.2 基于模糊模型的去噪算法(算法2)

图1 隶属函数模型

在实数域R中，模糊聚类通过隶属函数uA(x)将模糊集A中的任意元素映射到区间［0，1］中，即uA(x)∶A→［0，1］。确定隶属函数uA是模糊模型去噪算法的基础，常用的模糊聚类的隶属函数模型如图1所示。模糊聚类能够更加客观地反映细节信息。隶属函数在精确量向模糊量进行转化过程中起着非常重要的作用，不同的隶属函数对模糊模型的性能产生很大的影响，决定着系统的性能;同时，隶属函数是对客观事物的不分明性的定量描述，带有一定的主观性。所以需要根据实际情况选择隶属函数，并在实践中不断地学习和修正。

不同的隶属函数曲线形状产生不同的滤波去噪效果。通过模糊聚类算法使得聚类中心邻域范围内的像素在灰度域享有共同的属性，在此范围之外的像素对聚类中心的像素灰度值的作用减弱。图1a和b的隶属函数模型的分界点不易确定，基于模糊模型的去噪算法选择图1d曲腰梯形隶属函数模型，其函数表达式为

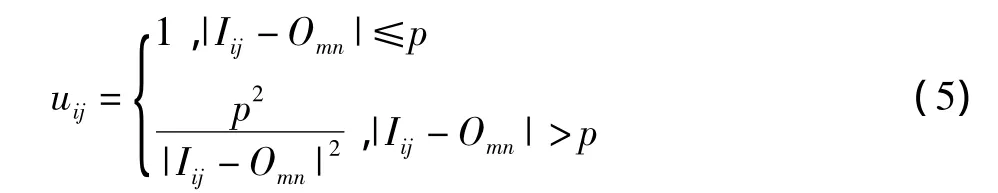
式中:p=λ·σε，本文算法中取λ=0.5。

p值的选取很大程度上决定了模糊模型去噪的性能，同时它的选择也增强了去噪模型设计的灵活性。算法2的步骤和硬聚类模型去噪算法相同，只是替换uij。充分考虑到耗费的运算时间，将算法1和算法2的迭代次数设定为10次。

2 实验结果分析

用平均绝对误差MAE、平均均方误差MSE和峰值信噪比PSNR对以上各方案的去噪性能进行评价。其定义分别为

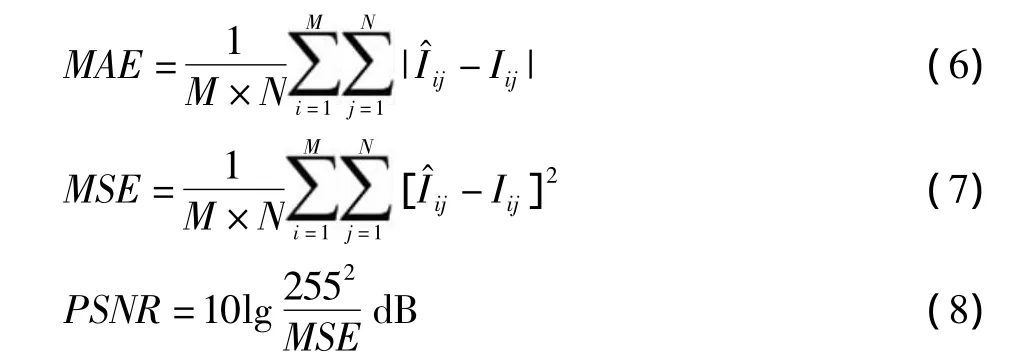
对于M×N的图像，MAE值越小表示图像细节处理效果越好，PSNR越大代表图像质量越好，该去噪算法的性能越好。

表1详细地给出了含脉冲噪声(30%)的图像去噪算法的客观评价数据，通过比较得出各算法的处理效果，即中值滤波＜算法1＜Model［6］＜算法2。

表1 对含脉冲噪声的图像去噪算法的比较

从图2和图3中可以得到:在上述去噪算法中，均值滤波去噪效果最差，其次是中值滤波。本文的算法1、算法2和利用文献［6］的模型(Model［6］)去噪效果较好，图像更加清晰。算法1、算法2和Model［6］的去噪能力与噪声密度紧密相关。随着噪声密度增加到一点的程度(图3中大约在48%)，真实信号与噪声信号各占一半，算法1对信号分类调整时出现错误的几率较大，使得去噪能力比中值滤波差，这也符合1.1节对硬聚类算法的去噪能力的理论分析。

图2 去除脉冲噪声的结果

图3 对含脉冲噪声的图像去噪算法的比较

同时，算法1和2去噪后的图像对比度比Model［6］要好;在其他条件相同的条件下，算法2处理后的图像MAE和MSE最小，PSNR最大。因此，基于模糊模型的去噪算法是一种较好的去除脉冲噪声的方法。

3 结论

本文采用硬聚类模型和模糊模型两种去噪算法对含脉冲噪声的图像进行去噪。当噪声密度越小时，即信噪比越大，聚类算法去除脉冲噪声的能力越强。基于模糊模型的去噪算法能够较好地去除脉冲噪声，提高信噪比和保护图像细节;同时，在实现上简单易行，能够保持较好的实时性，适用于移动显示终端的辅助功能。

［1］CELIKYILMAZ A，TURKSEN I B.Enhanced fuzzy system models with improved fuzzy clustering algorithm［J］.IEEE Trans.Fuzzy Systems，2008，16(3):779－794.

［2］BUADES T，LOU Y，MOREL J M，et al.A note on multi－image denoising［C］//International Workshop on Local and Non－Local Approximation in Image Processing，2009.Tuusula，Finland:IEEE Press，2009:1－15.

［3］CHEN P，LIEN C.An efficient edge－preserving algorithm for removal of salt－ and － pepper noise［J］.IEEE Signal Processing Letters，2008，15:833－836.

［4］JANAH N Z，BAHARUDIN B.Mixed impulse fuzzy filter based on MAD，ROAD，and genetic algorithms［C］//2009 International Conference of Soft Computing and Pattern Recognition.［S.l.］:IEEE Press，2009:82－87.

［5］DONG Yiqiu，XU Shufang.A new directional weighted median filter for removal of random－valued impulse noise［J］.IEEE Signal Processing Letters，2007，14(3):193－196.

［6］HORIUCHI T，WATANABE K，TOMINAGA S.Adaptive filtering for col－or image sharpening and denoising［C］//Proc.14th International Conference of Image Analysis and Processing.［S.l.］:IEEE Press，2007:196－201.

［7］廖彬，冯穗力，叶梧.基于H.264的差错掩盖技术的研究［J］.电视技术，2005，29(1):26－28.