伪码FFT快捕恒虚警门限的研究

杨晓波，冯冀宁，王 薇

(1.石家庄职业技术学院，河北 石家庄 050081;2.河北师范大学电子工程系，河北 石家庄 050031)

0 引言

对于时域相关信号检测的包络检波和平方检波方式下的虚警门限的确定，文献［1］给出了详细的推导和可靠的结论。FFT捕获是伪码快速捕获的主要方式［2］，伪随机码频域快捕属于二元信号检测，因为这种捕获方式是通过频域作相关，然后相关输出最大相关值和门限比较来寻找伪随机码的相位，如果每一个相关输出值都认为是服从某种分布的随机变量，在所有相关输出中找最大值和门限进行比较判断信号有无的这种情况下，门限的确定就不能单纯地根据每个随机变量的分布来确定，此时要根据最大值分布来确定门限，之前的文献中还没有发现关于在这种情况下的门限的确定方法研究和结论，本文就在包络检波和平方检波方式下，FFT伪随机码快捕如何确定虚警门限进行了研究。

1 时域搜索方式及虚警门限的确定

伪码捕获是对接收信号的多普勒频率和码相位进行估计，实质为一个二维搜索过程。一个多普勒频率单元和一个码相位单元构成一个信号搜索单元。信号时域(码相位)/频域(多普勒频率)搜索方式如图1所示。

图1 C/A码的二维搜索方式

一般用恒定的多普勒分格，时域上每次移动1/2码相位，对I，Q进行积分和累加，并且计算包络，将每个包络和门限相比较以确定卫星信号是否存在，由于每个方格要么包含噪声和信号，要么只有噪声没有信号，因此信号检测过程是一个二元假设检验过程，上述两种情况均有其概率密度函数［1］，在有信号的情况下，包络是服从莱斯分布的随机变量，其概率密度函数为

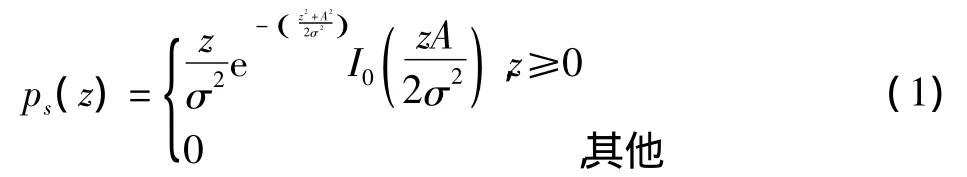
式中:z为随机变量;σ为均方根噪声功率;A为信号幅度均方根;I()为零阶修正的贝塞尔函数。式(1)用预检0测信号与噪声之比表达，当包络检测器的信噪比为S/N(单位为dB)时

式中:s/n为预检测信号和噪声之比为A2/2σ2，s/n=10S/N/10。对于没有信号的情况下，式(2)中A=0，得到没有信号时包络的概率密度函数为

服从瑞利分布，对在恒定虚警下，式(3)以虚警门限为积分限积分，用单次试验虚警概率和可测量的σ噪声功率表示门限为

通过式(4)可以看出，虚警门限是和噪声功率及事先确定的虚警概率决定的。

2 频域搜索方式及门限的确定

2.1 包络检波虚警门限

文献［3］介绍了码相位的频域搜索方式，在频域通过快速傅里叶变换，通过一次运算搜索某一频点的所有码相位，其原理如图2所示。

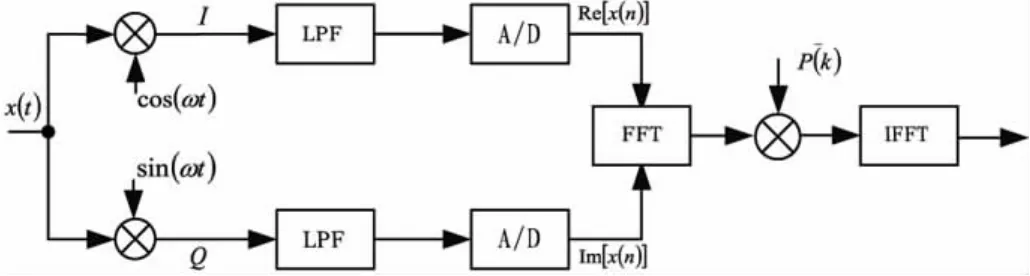
图2 伪随机码快捕的频域搜索原理

GPS信号C/A码速率为1.023 Mchip/s，采样率fs=32.768 Msample/s，则一个C/A码周期TC/A=1 ms的采样输出为 x［n］，n=1，2，…，32 768，共有 32 768 个采样点，x［n］=I［n］+iQ［n］。本地码为 y［n］，n=1，2，…，32 768，则有

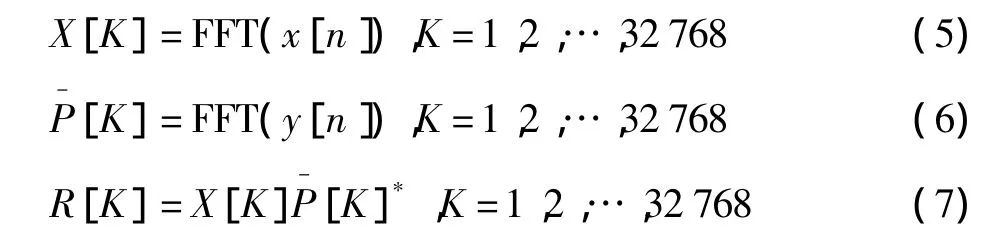
r［m］= ｜IFFT(R［K］)｜，m=1，2，…，32 768 即对应的所有码相位的相关输出，然后找最大值rmax和门限比较。此时，包络仍服从瑞利分布，但是恒虚警门限的确定要根据所有服从瑞利分布的独立随机变量 r［m］，m=1，2，…，32 768 的最大值 rmax的概率密度函数来确定。n个独立同分布的随机变量的最大值的概率密度函数为［4］

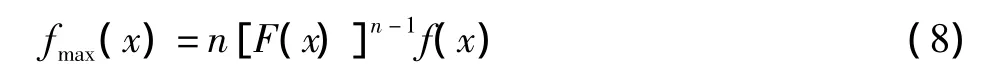
则通过式(3)推导得出相关输出最大值的概率密度函数为

由式(12)可以看出，虚警门限不仅和虚警概率及噪声的均方差功率有关还和相关输出值的个数有关。对于相同的虚警率和噪声功率，不同的相关个数下，虚警门限是不同的，这和时域相关输出的门限是有区别的。有时信号检测使用平方检波方式，本文就该方式下的虚警门限也进行了推导。

2.2 平方检波虚警门限

平方检波相关积累输出为I2+Q2，在没有信号的情况下是服从指数分布的随机变量［1］，下面求随机变量中最大值的分布。指数分布概率密度函数为

由式(18)可以得出门限和相关输出值的个数有关，同时还可以看出对于指数分布的随机变量，2σ2为其均值，所以在确定门限时可以直接利用噪声均值的估计、Pfa和相关输出的个数来确定。

3 仿真结果

图3为16384点相关输出0.1%恒虚警，1000次仿真下，相关输出最大值和门限的关系图。

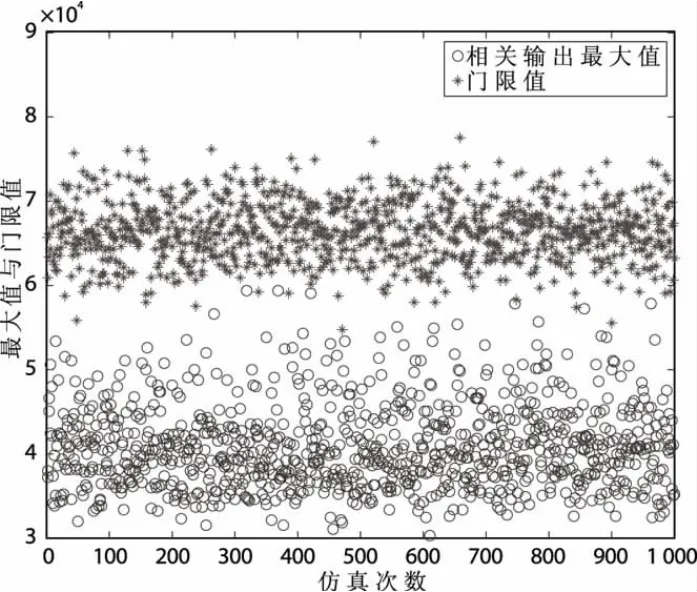
图3 伪随机码快捕32 768点IFFT输出最大值和门限的关系

表1列出了通过仿真得出的在不同相关输出个数、检波方式、仿真次数下最大值过门限的次数，可以看出，有一定的误差，这和噪声功率或噪声均方差的估计偏差有关，但总体上能够验证根据本文结论确定的门限是可靠的。

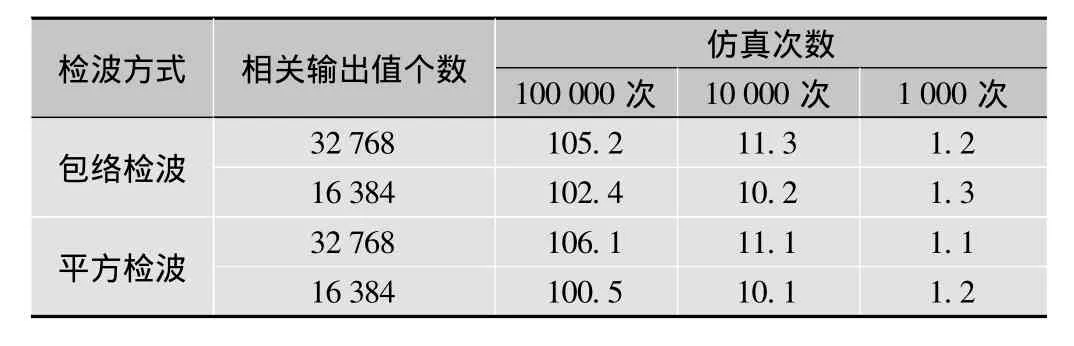
表1 不同相关输出个数、检波方式、仿真次数的最大值过门限的次数

4 结论

通过本文的结论可以确定伪随机码频域快捕单次检测的虚警门限，由于包络检波和平方检波输出的概率密度函数涉及到零阶贝塞尔函数的积分，其结果非常的繁琐，并且其闭式解涉及到零阶贝塞尔函数的近似［5］。所以在虚警门限下的检测概率的确定还是需要在不同信噪比下通过仿真的方式确定，在很多情况下，尤其是弱信号检测需要作多次非相干积累后再对信号的有无进行判断，此时随机变量已没有确定的概率密度函数，这种情况下虚警门限和检测概率也需要通过仿真来确定。

［1］KAPPLAN E D.GPS原理与应用［M］.秋致和，王万义，译.北京:电子工业出版社，2002.

［2］杨晓波，王薇.一种扩频系统频域干扰抑制稳健加窗方法研究［J］.电视技术，2011，35(7):128 －131.

［3］VAN NEE D J R，COENEN A J R M.New fast GPS code－acquisition technique using FFT［J］.IEEE Trans.Electronics Letters，1991，27(2):158－160.

［4］沈恒范.概率论与数理统计教程［M］.北京:高等教育出版社，1995.

［5］庄铭杰.计算机仿真无线Rice衰落信道的实现方法［J］.电波科学学报，2004，19(5):632－637.