一类具时滞和非线性传染率的SIS传染病模型的Hopf分支

童姗姗，窦霁虹，王佳颖

（西北大学数学系，陕西西安710127）

一类具时滞和非线性传染率的SIS传染病模型的Hopf分支

童姗姗，窦霁虹，王佳颖

（西北大学数学系，陕西西安710127）

研究了一类具恢复期时滞且发生率为非线性的SIS传染病模型，讨论了该系统地方病平衡点的稳定性。利用Hopf分支理论，以时间τ为参数给出了系统在地方病平衡点处产生Hopf分支的充分条件。

Hopf分支；时滞；非线性传染率；局部渐近稳定

近二十年来，许多学者通过数学模型研究传染病动力学，已有很多成果［1］。传染病动力模型中，最重要的是对发生率的描述，在经典的流行病模型［2-4］中通常采用双线性发生率（βSI）和标准发生率，同时，对发生率为非线性［5-6］的传染病模型也有一些研究成果。

2009年杜艳可等在文献［7］中研究了如下一类具非线性发生率βISp的SIS传染病模型：

讨论了其平衡点以及极限环的性态。

SIS传染病模型特性主要体现在染病者被治愈变为易感者的恢复阶段，故考虑恢复期时滞更具实际意义。本文考虑系统（1）中p=2时，加入疾病恢复期时滞 τ，讨论一类具有常数输入和发生率为βIS2的SIS传染病模型的地方病平衡点稳定性与Hopf分支，即

这里，S（t），I（t）分别表示t时刻易感者的数目，感染者的数目，δ表示种群的自然死亡率，δA表示对种群的输入率（其中A为无病状态下总种群处于平衡时的个体数），βI（t）S2（t）表示疾病的传染率，d表示感染者的死亡率，d=δ+ε，ε表示感染者的因病死亡率，α表示感染者的恢复率，τ≥0为恢复滞后时间，根据生态学意义，δ、A、β、d、ε、α都为正常数。将系统的两个方程相加，得到

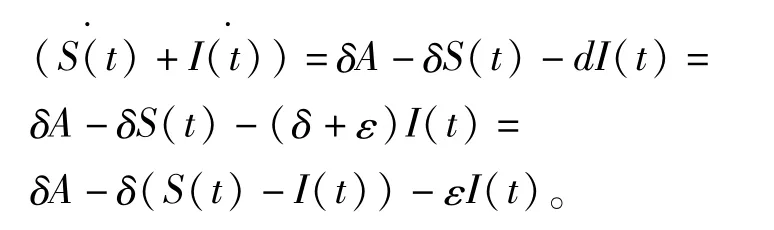
由于I（t）≥0，所以

1 平衡点分析

2 地方病平衡点的稳定性及Hopf分支的存在性

为求E*（S*，I*）的近似线性系统，作变换：变换后仍用S，I记X，Y。得到系统在E*（S*，I*）的近似线性系统为：

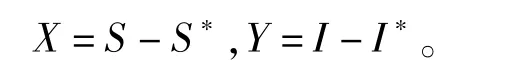
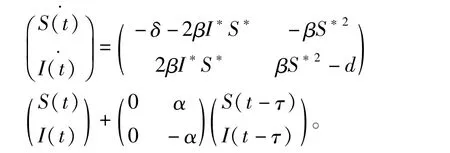
特征方程为：

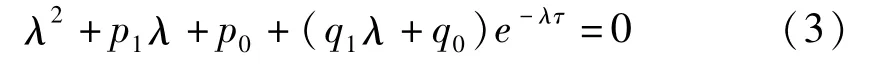
其中：

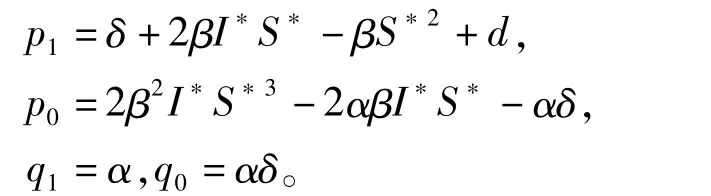
当τ=0时，（3）式变为

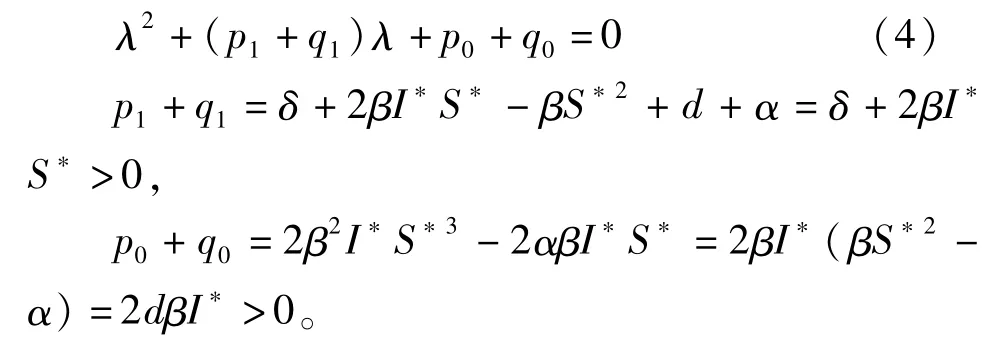
由Routh-Hurwits判据知特征方程（4）的根均具有负实部，即τ=0时地方病平衡点E*（S*，I*）在Ω内局部渐近稳定。

假设存在某个τ＞0，使方程有纯虚根λ=±iω（ω＞0），代入方程得-ω2+p0+q1ωsinωτ+ q0ωcosωτ+i（p1ω+q1ωcosωτ-q0sinωτ）=0。

则有方程组：

由方程组（5）得：

其中：

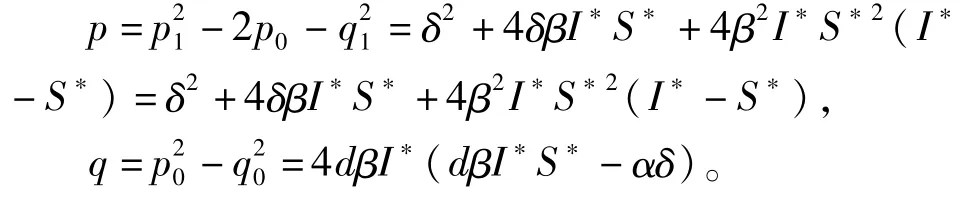
则方程两根为：

引理1 （i）当p＞0且q＞0或Δ＜0时，对于任意的τ≥0特征方程（3）的所有根皆具有负实部。

（ii）当q＜0或p＜0且Δ=0时，且τ=τk+时，方程（3）有一对纯虚根±iω+，当τ=τ0+时，方程的根除±iω+之外都具有负实部。

（iii）当q＞0，p＜0且Δ＞0时，且τ=τk+（τ= τk-）时，方程（3）有一对纯虚根±iω+（±iω-），当τ =τk+（τ=τk-）时，方程的根除±iω+（±iω-）之外都具有负实部。

其中由方程组（5）得：

相应于ω±的τk±为

对于系统（2），通过计算分析可知当满足

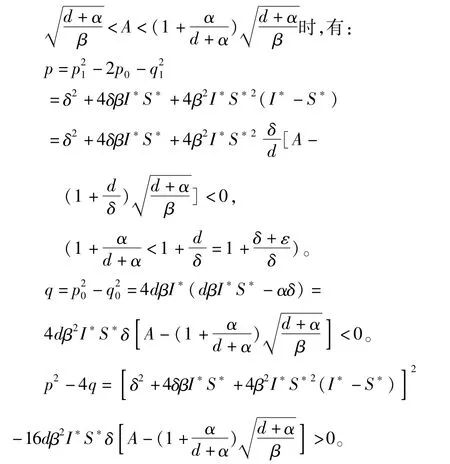
故当τ∈［0，τ0+）时，方程的根都具有负实部，当τ=τ0+时，方程有一对纯虚根±iω+，当τ＞τ0+时，方程的根至少有一个有正实部。

相应于ω+的τk+为

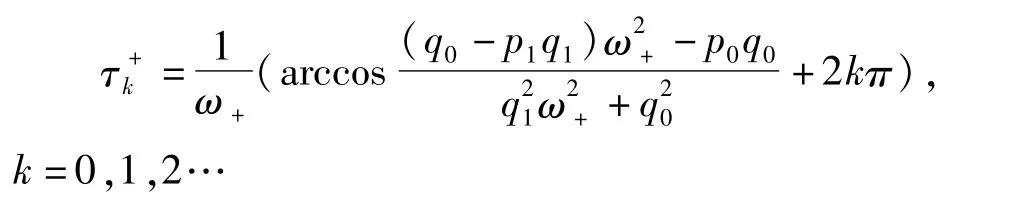
对方程（5）两边关于τ求导得

［（2λ+p1）+q1e-λτ-τ（q1λ+q0）e-λτλ（q1λ+q0）e-λτ有

因此

综上，结合引理1，Hopf分支定理的条件满足，从而在E*的附近分支出周期解，有以下结论：

（i）当τ∈［0，τ0+）时，系统（2）的地方病平衡点在Ω内是局部渐近稳定的，当τ＞τ0+时，系统（2）的地方病平衡点不稳定。

（ii）当τ=τk+（k=0，1，2，…）时，方程除有一对纯虚根±iω+外，其他根均具有负实部，此时系统（2）在E*（S*，I*）处产生Hopf分支。

3 小结

本文研究了一类具有恢复期时滞和非线性发生率的SIS传染病模型，分析了地方病平衡点的局部渐近稳定性与Hopf分支，当时滞τ由0变化到临界值时，系统在地方病平衡点附近发生Hopf分支，即当τ增加通过临界值时，从地方病平衡点分支出周期解，此时，疾病会出现周期震荡现象。

［1］马知恩，周义仓，王稳地等.传染病动力学的数学建模与研究［M］.北京：科学出版社.

［2］王文娟，辛京奇.一类具有阶段结构和分布时滞的种群-传染病模型［J］.数学的实践与认识，2010，40（14）：114-120.

［3］徐金瑞，王美娟，张拥军.一类具有标准发生率的SIS型传染病模型的全局稳定性［J］.生物数学学报，2010，25（2）：249-256.

［4］郭金生，李晓燕.一类有双线性发生率的传染病模型的定性分析［J］.重庆工学院学报（自然科学版），2008，22（2）：44-46.

［5］Heesterbeek JA P，Metz JA J.The saturating contact rate in marriage and epidemicmodels［J］.J.Math.Biol.，1993，31：529-539.

［6］Weimin liu，H W Hethcote，S A Levin.Dynamical behavior of epidemiologicalmodelswith nonlinear incidence rate［J］. J.Math.Biol.，1987，25：359-380.

［7］杜艳可，徐瑞，段立江.一类具有非线性发生率的SIS传染病模型的定性分析［J］.西南大学学报，2009，31（3）：9 -13.

［责任编辑 贺小林］

Hopf Bifurcation of a SIS Epidem ic M odel w ith Time Delay and Nonlinear incidence

TONG Shan-shan，DOU Ji-hong，WANG Jia-ying

（Department of Mathematics，Northwest University，Xian 710127，China）

A class of an SIS epidemic mathematic model with constant recruitment，time delay and nonlinear incidence is studied，and its stability of endemic equilibrium is discussed.By applying the theorem of Hopf bifurcation，the sufficient conditions of the endemic equilibrium occurring Hopf bifurcation with delay as parameter is given.

Hopf bifurcation；time delay；nonlinear incidence；local asymptotic stability

O175.1

A

1004-602X（2011）03-0019-03

2011- 05- 16

童姗姗（1986—），女，河南南阳人，西北大学在读研究生。