永磁偏置径向磁轴承的原理分析与参数设计

赵旭升 邓智泉 汪 波

（1.南京航空航天大学自动化学院 南京 210016 2.南京化工职业技术学院自动控制系 南京 210048）

1 引言

伴随着现代航空业的发展需求，高速电动机以其体积小、重量轻等特点，在提升航空航天器的工作性能方面具有极其重要的意义，因而高速电动机的研究与发展迅速，同时民用工业领域对高速电动机的需求也日趋广泛[1-2]，这也使磁轴承技术得到了广泛的应用，但作为高速电动机中的重要组成部分其需要具有体积小、功耗低的特点。永磁偏置磁轴承利用永磁体提供偏置磁场，控制绕组只提供平衡负载和外界干扰的动磁场，控制绕组的安匝数大大减小，缩小了磁轴承的体积，减轻了磁轴承重量，减少了功率损耗，提高了轴承的空间利用率和磁电效率，使其在储能飞轮、动量飞轮及高速电动机等领域具有广泛的应用前景[3-7]。本实验室研究了一种五自由度高速磁悬浮电动机，其一端采用一种永磁偏置轴向径向磁轴承[3-4,8-9]，另一端需采用一种径向磁轴承，共同实现高速电动机转子的五自由度悬浮。文献[10-12]中分别研究了多种永磁偏置径向磁轴承，定子磁极都为异极性排列，高速旋转时，在转子铁心中会产生较大的涡流和磁滞损耗。文献[13]研究了一种定子加装永磁体的永磁偏置径向磁轴承，定子磁极为同极性排列，磁滞损耗小，其利用位于永磁体两侧的两个径向定子实现转子的两自由度悬浮，但其定子磁极共计绕有八个控制绕组，使其轴向长度较长，不利于转子临界转速的提高。Satoru Fukata提出了一种转子套装永磁体的永磁偏置径向磁轴承[14]，其利用轴向充磁的永磁体套装在转子上产生偏置磁通，也为同极性结构，但其永磁体充磁长度较长，磁阻较大。同时，这种转子结构在高速旋转时永磁体需利用碳化纤维进行包裹，增加了机械加工和安装的难度。本文研究了一种永磁偏置径向磁轴承，与现有永磁偏置径向磁轴承相比，结构更为紧凑，控制方便，在磁悬浮高速电动机系统中有着广泛的应用前景。

2 永磁偏置径向磁轴承的结构及工作原理

2.1 永磁偏置径向磁轴承结构

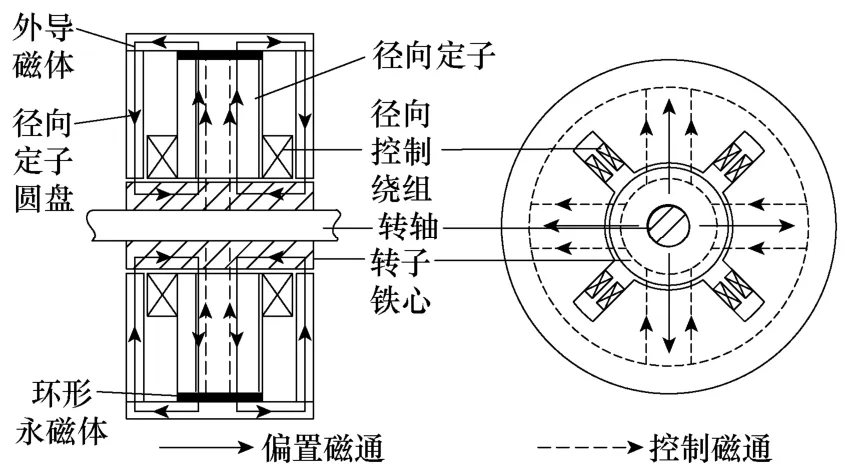
图1 永磁偏置径向磁轴承结构及磁路图Fig.1 Structure and magnetic circuit of permanent magnet biased radial magnetic bearing

永磁偏置径向磁轴承结构如图1所示，其由外导磁体、两侧径向定子圆盘、转子铁心、转轴、径向定子、径向控制绕组、环形永磁体等部件构成。其中，外导磁体、定子圆盘均由实心软磁材料（电工纯铁）制成，为便于高速旋转，转子铁心也由实心软磁材料制成；径向定子为四齿两对极结构，由硅钢片叠压而成，线径和匝数都相同的径向控制绕组套装在磁极上，相对两个齿上的绕组串联连接；径向充磁的环形永磁体采用烧结钕铁硼，嵌于定子圆筒内表面和径向定子外表面之间；转子铁心套装在转轴上，与径向定子和径向定子圆盘形成径向气隙。从图1可见，转子铁心长于径向定子，有利于消除定转子不对齐所产生的单侧磁拉力。

2.2 永磁偏置径向磁轴承工作原理

永磁偏置径向磁轴承磁路图如图1所示。环形永磁体产生偏置磁通（图1中实线所示），经外导磁体、定子圆盘、圆盘下气隙、转子铁心、径向气隙和径向定子形成闭合磁路。径向控制磁通（图1中虚线所示）在径向定子、径向气隙、转子铁心形成闭合回路。从图1可见，两侧定子圆盘只用作偏置磁路，可制成薄片圆盘（只需磁通不超过软磁材料饱和磁通），缩短了磁轴承的轴向长度，有利于转子临界转速的提高。

由于结构对称，当转子位于中心位置时，四个径向气隙的偏置磁通密度分别相等，转子受到的悬浮力为零。假定此时转子偏离平衡位置向下有一微小位移，则径向控制绕组通以控制电流在径向气隙中产生控制磁通与偏置磁通叠加，上气隙中磁场增强，下径向气隙中控制磁通与偏置磁通方向相反，磁场减弱，在转子上产生向上的悬浮力。若转子向上有一微小位移，则控制电流反向，形成的控制磁通反向与偏置磁通叠加，形成向下的悬浮力。同理，在水平方向可以得出类似的结论。

3 永磁偏置径向磁轴承的数学模型

3.1 等效磁路分析

由图1中的偏置磁路和控制磁路可见，两侧定子圆盘只作为偏置磁路，控制磁通只经过径向气隙，在有限元分析软件中建立二维轴对称结构模型来进行磁轴承的电磁场仿真，并对径向定子进行了相应的等效。偏置磁场的二维仿真结果如图2a所示。从偏置磁场的磁力线图中可以看出，该型磁轴承有一个主要的漏磁路，即定子圆盘与径向定子之间的漏磁通。在此基础上可得到该型磁轴承的偏置等效磁路图，如图3a所示。图2b为该型磁轴承控制磁通的二维仿真图，从图2b可见，在平衡位置处，垂直方向的控制磁通对水平方向几乎没有影响。在图2b的基础上可得到控制磁场等效磁路图，如图3b所示。由于磁场具有较强的发散性，在气隙处，由于空气磁导率低，磁力线会向外膨胀，在分析和计算时需要考虑气隙处漏磁的影响（在设计时对漏磁和软磁材料磁阻都加以补偿）。

图2 永磁偏置径向磁轴承二维仿真图Fig.2 2-D magnetic field simulation of permanent magnet biased radial magnetic bearing

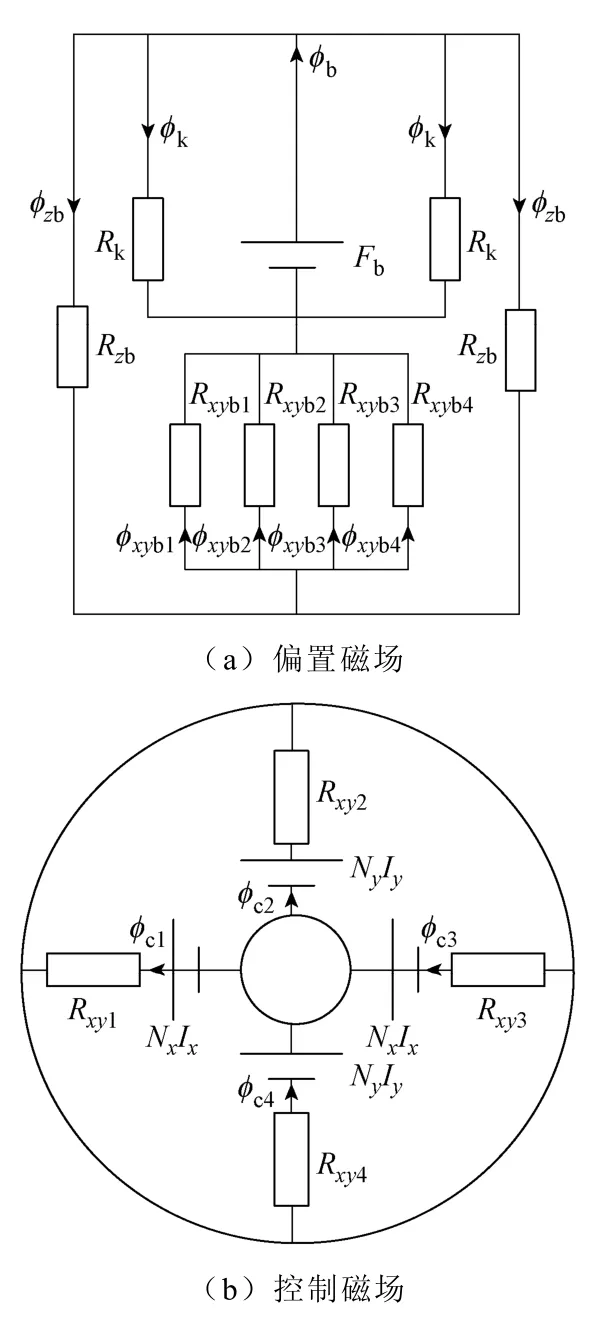
图3 永磁偏置径向磁轴承等效磁路图Fig.3 The equivalent magnetic circuit of permanent magnet biased radial magnetic bearing

图3 中，Fb为永磁体对外提供的总磁动势，φb为总的偏置磁通，Rk为漏磁阻，φk为漏磁通，NI为径向控制绕组安匝数，φc为径向控制磁通，Rxy1～Rxy4径向气隙磁阻，φxyb为径向气隙偏置磁通，RAb、RBb为径向定子圆盘气隙磁阻，φAb，φBb为径向定子圆盘气隙偏置磁通。现假设转子铁心沿径向正方向偏离一微小位移，则径向气隙磁阻为

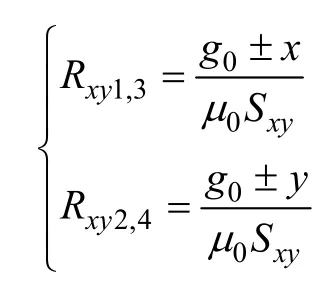
圆盘下气隙磁阻可近似认为

式中，μ0为空气磁导率；g0为径向气隙长度；Sxy为径向磁极面积；gb为定子圆盘气隙长度；SD为定子圆盘面积。

根据图3a并利用磁路基尔霍夫定律可求出气隙下的偏置磁通

一般磁轴承系统正常工作时，高速悬浮转子最大允许的偏心位移是气隙长度的十分之一，则可认为两个径向方向的控制磁通是彼此解耦的[15]，由图3b可求出控制磁通

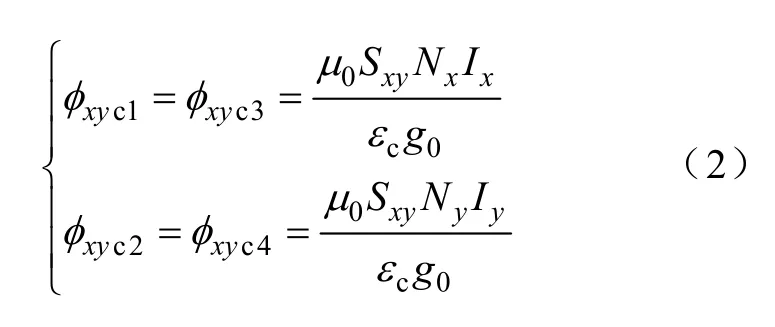
式中，εc为控制磁通在气隙处的漏磁系数。

3.2 径向悬浮力方程

以坐标轴的正方向为力的正方向，以产生正方向的力的电流方向为电流正方向，有

式中，Spxy为侧的径向定子磁极投影面积，其与径向定子磁极面积Sxy关系为

式中，α为径向磁极弧度。

式中，fi为定子占空率，np为磁极数。

由于磁极间隙的存在所引起气隙磁通的变化，在转子上产生了较大的涡流损耗，所以在设计径向定子时，要尽可能减小磁极间间隙，但过小，又会带来绕组的嵌线困难，设定了定子占空率，实际就确定了径向定子的槽宽。

对Fx,y在平衡位置附近进行线性化处理并略去二阶以上无穷小量得

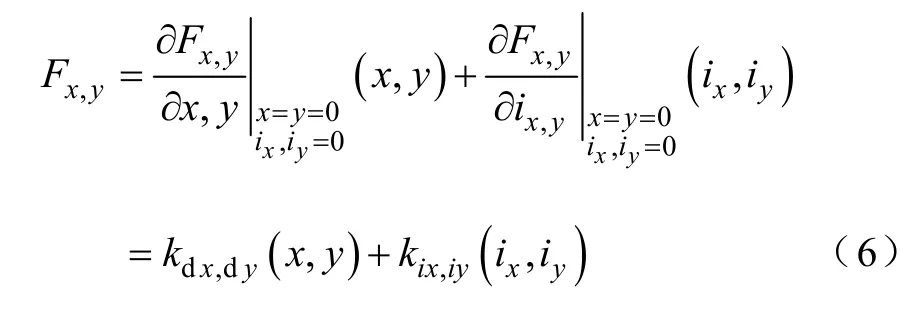
式中，kdx，kdy为力-位移系数，

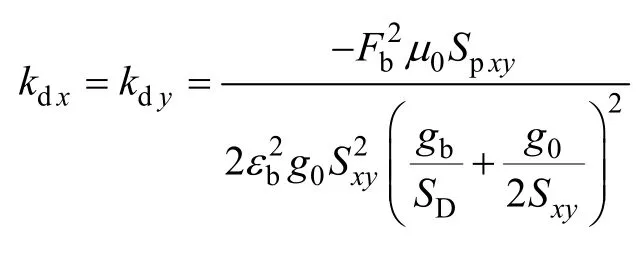
式中，kix，kiy为力-电流系数,

值得注意的是，两侧作为偏置磁路的定子圆盘，在转子位于中心位置时，由于结构的对称性，转子受到的作用力合力为零，而当转子偏离中心位置时，定子圆盘对转子的作用力合力不再为零，且方向与转子偏离的方向一致，这个偏心拉力需要径向控制磁场的调节来补偿，则会导致控制绕组中的电流波动较大。针对这一缺点，在实际应用时可采用特殊的控制策略将这一缺点转化为优点，如利用偏置磁场不平衡产生的力来抵消外部负载力，从而实现控制电流减小至零的零电流控制策略。

4 永磁偏置径向磁轴承的参数设计

4.1 气隙磁通密度的确定

本文在参数设计时将软磁材料的静态工作点取在磁导率最大变化处[16]，参考硅钢片及电工纯铁这两种软磁材料的磁化曲线，将气隙磁通密度设计为1.2T，气隙磁通包含偏置和控制磁通，在此取气隙偏置磁通密度Bxyb稍大于软磁材料饱和磁通密度的一半，以增加永磁材料充磁方向的厚度。气隙中控制磁通密度设定为Bxyc稍小于软磁材料饱和磁通密度的一半，降低气隙中控制磁场磁通密度可以减少控制绕组的匝数，从而降低控制绕组的功率损耗。但两者的合成磁密应工作在软磁材料磁化曲线的线性段。

4.2 径向定子磁极面积的确定

由式（3）可进而得出径向悬浮力Fxy

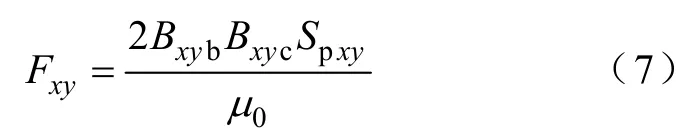
根据转子重量及转速需求，明确所需悬浮力的大小，利用式（7）及式（3）可求出径向磁极面积的大小。

4.3 径向控制绕组

利用求得的径向磁极面积结合等效磁路图，可求出径向控制绕组的安匝数

式中，fxyc为控制磁通磁阻系数，明确气隙长度g0（0.1～1.5mm），由导线电流密度（一般取4～6A/mm2）选取相应导线，确定出控制绕组的截面积Sw。

式中，dm为导线直径。

4.4 定转子各结构参数的设计

为避免转子铁心软磁材料饱和，应保证转子铁心中合成磁通小于设定值，即式中，ri为转轴半径，rj为转子半径

另有rj和前述的占空率的相互关系，可求解出径向磁极的宽度bp、定子槽宽ta和轴向长度ls，即

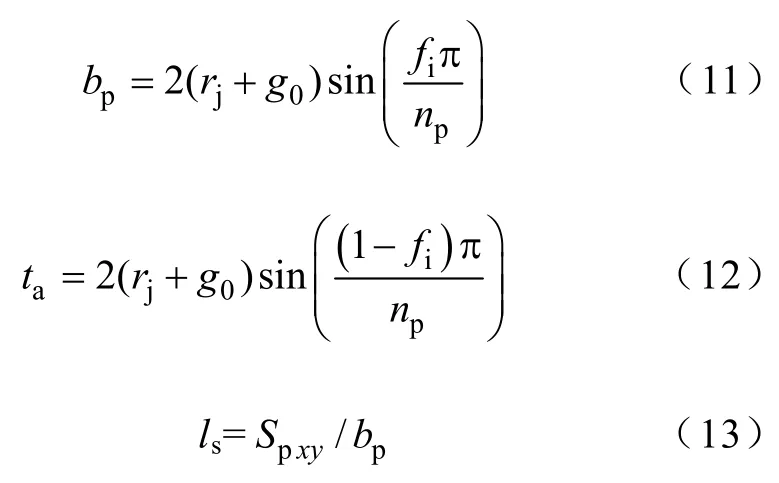
由绕组的截面积和槽宽求解出定子齿高hp

式中，φ为绕组系数，取0.6～0.8。

定子磁轭hr的高度为

在设计永磁体时可对其高度进行适当调整，但应保证定子齿轭中的控制磁通密度不至于饱和。

根据等效磁路图2a，定子圆盘气隙磁路和径向气隙磁路为上下串联关系，且定子圆盘只作为偏置磁路，为缩短整个磁轴承的轴向长度，可将其偏置磁密值设定的较高，只需保证

式中，BAb为定子圆盘气隙偏置磁通密度，la为定子圆盘轴向长度。

4.5 偏置磁路的参数设计

根据等效磁路图3a，有

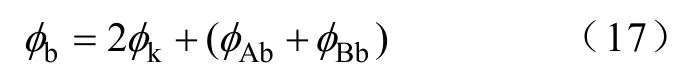
忽略气隙间的漏磁系数差异，定子圆盘气隙偏置磁通量为

式中，Dsmi为径向定子内径为径向定子外径，

4.6 永磁体参数的设计

采用径向充磁的环形永磁体的结构参数包括径向充磁厚度Tp及轴向长度Lp。根据磁轴承的几何关系，永磁环内径等于径向定子外径，Hc为永磁材料矫顽力，Br为剩余磁密，其退磁曲线接近直线，用公式可表示为

式中，μp为永磁体的磁导率，为永磁体工作点参数。

由于在工程实践中，永磁体的加工受工艺水平、性价比等客观条件的限制，因此在设计时可将永磁环的充磁厚度设为定值，其数值的选择应尽量使计算出的永磁体工作点位于其最大磁能积点附近。从等效磁路图可得

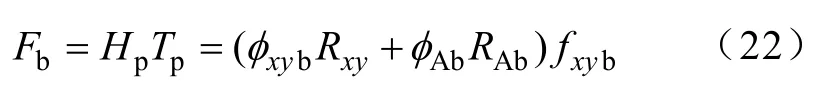
式中，fxyb为偏置磁通磁阻系数。

根据求得的Hp，再结合永磁体的磁化曲线可求得Bp大小，则永磁体的中性面面积Sp为

根据几何关系，可得永磁环轴向长度为

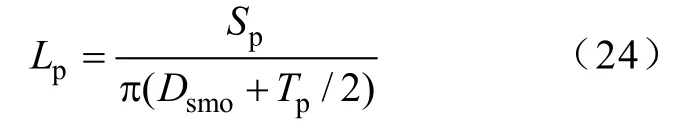
根据几何关系，永磁环轴向长度不应大于定子磁轭轴向长度。

5 仿真和实验

5.1 设计要求和设计结果

表1给出了承载力的设计要求、转轴尺寸及其他设计参数。利用上述一系列公式可求出磁轴承参数。

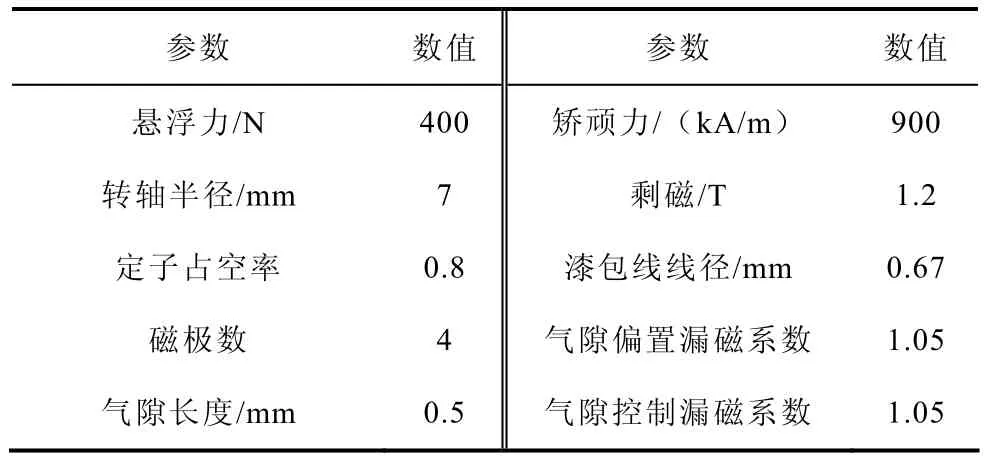
表1 设计要求和已知参数Tab.1 Requirements and known parameters

利用上述一系列公式可求出磁轴承参数，表2给出了设计结果。

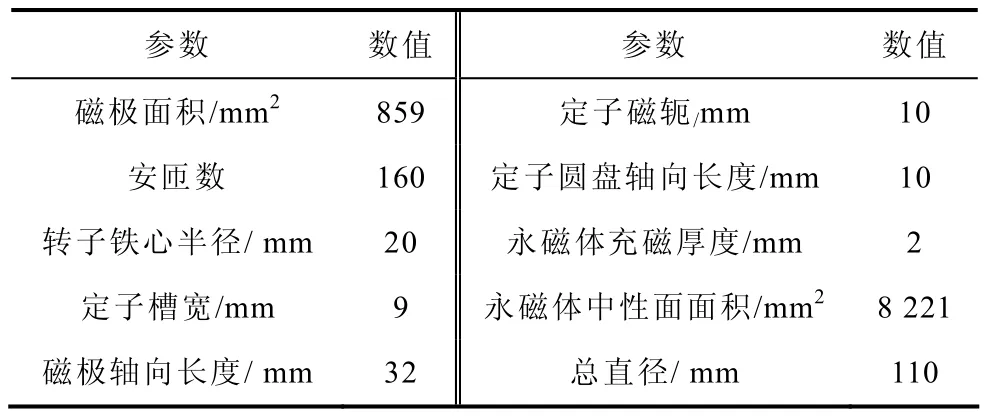
表2 设计结果Tab.2 Design result

5.2 有限元仿真分析

采用有限元分析软件ANSOFT12.1对设计结果进行了磁路仿真分析，以验证永磁偏置径向磁轴承结构设计的合理性和参数设计的正确性。建立三维磁场对永磁偏置径向磁轴承进行了仿真分析，分别分析了偏置磁通的磁密分布、加径向励磁时的合成磁通磁密分布及受力情况。

图4a所示为永磁偏置磁通在磁极中的分布，径向气隙中偏置磁通密度接近于0.83T，定子圆盘气隙偏置磁密接近于1.1T，符合设计要求。

图4b模拟了最大悬浮力情况下的有限元验证，此时，对控制绕组施以160安匝的励磁电流，偏置磁场和控制磁场共同作用时合成磁通的磁力线分布，此时一侧气隙磁通密度约为0.5T左右，另一侧接近于1.2T，转子铁心的径向合力为381N，符合设计要求。

图4 永磁偏置径向磁轴承磁通分布有限元仿真图Fig.4 Finite element simulation of permanent magnet biased radial magnetic bearing

根据设计结果，再利用磁路法和有限元分析两种方法对磁轴承性能曲线进行计算，如图5所示。其中图5a为径向力-电流关系曲线，图5b为径向力-位移关系曲线。从图中可以看出，由于磁路分析中忽略了软磁材料的铁心磁阻及考虑了气隙处的漏磁系数，因而在偏置位移及电流较小时与有限元场分析的结果较为接近。但图5b中仿真值稍大于理论值，这是两侧定子圆盘对转子所产生的被动磁拉力所致。

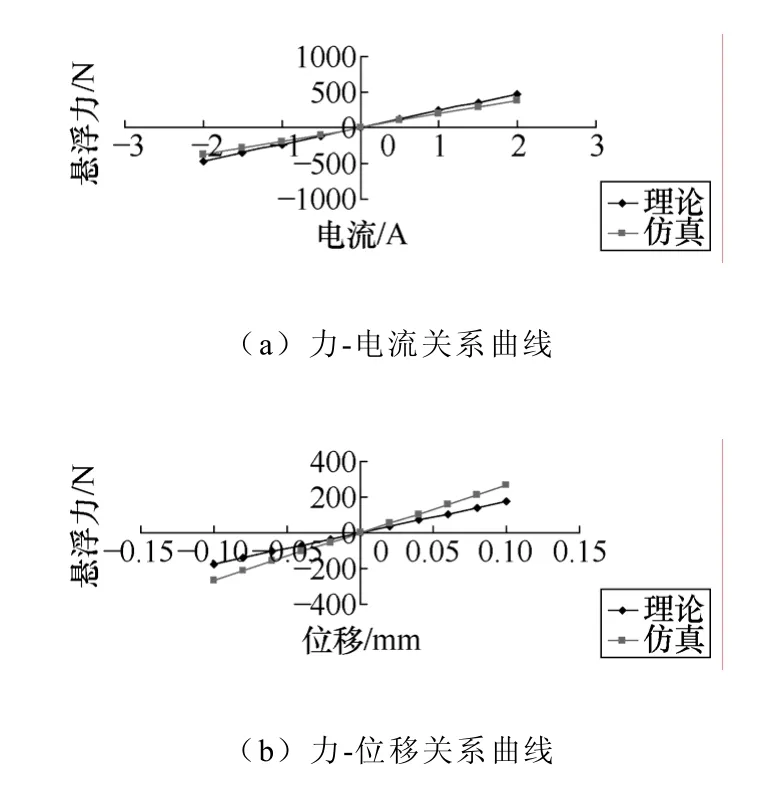
图5 永磁偏置径向磁轴承计算结果Fig.5 The calculation results of permanent magnet biased radial magnetic bearing

5.3 实验结果

利用仿真验算后的设计结果制作了永磁偏置径向磁轴承的原理样机如图6a所示，磁悬浮高速电动机整体样机如图6b所示，构建的五自由度磁悬浮高速电动机实验系统示意图如图6c所示。

利用模拟PID控制器对永磁偏置径向磁轴承样机的每个自由度独立控制，进行了悬浮实验。图7a给出了永磁偏置径向磁轴承两个自由度的静态起浮实验波形，转子在30ms的调节时间内实现了稳定起浮；图7b则给出了永磁偏置径向磁轴承两个自由度的冲击实验波形，永磁偏置径向磁轴承在15ms的调节时间内重新实现转子的稳定悬浮。对磁悬浮高速电动机系统进行了高速运行，实现了磁悬浮转子的高速旋转；图7c给出了永磁偏置径向磁轴承在20 000r/min时的径向位移波形和电流波形，转轴在各自由度的位移波动约为转轴与辅助轴承之间气隙长度的5%，即25µm，各自由度控制绕组中电流的平均值约为0.5A，峰-峰值约为2A。实验结果表明，该型永磁偏置径向磁轴承悬浮性能较为优良。

图6 永磁偏置径向磁轴承原理样机及实验系统图Fig.6 Prototype and experiment system of permanent magnet biased radial magnetic bearing

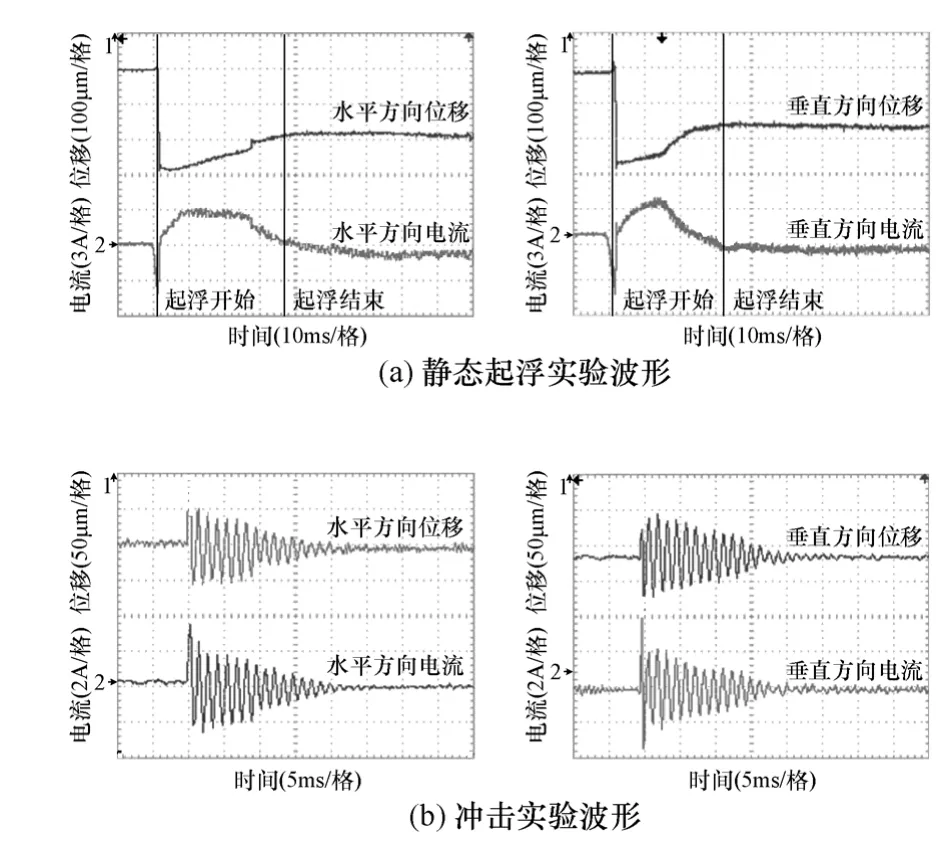
图7 永磁偏置径向磁轴承实验波形Fig.7 Experimental waveforms of permanent magnet biased radial magnetic bearing

6 结论

（1）永磁偏置径向磁轴承利用径向充磁的环形永磁体提供偏置磁通，控制绕组的安匝数得以减少，功耗得以降低。

（2）只需两对极、四个控制绕组控制两自由度悬浮，径向定子两侧定子圆盘只用作偏置通路，可制成薄片，使其结构更为紧凑，缩小了整个磁轴承的体积。

（3）以径向承载力为设计目标，明确所需的偏置磁场与控制磁场的磁通量的大小，计算出磁极面积和控制绕组安匝数；为避免软磁材料的饱和、减小转子铁心的涡流损耗优化设计磁轴承的定转子各参数；考虑工程实践的要求，优化设计永磁体的参数设计方法合理。

（4）永磁偏置径向磁轴承具有整体体积小、承载力大、效率高及成本低等特点，与永磁偏置轴向径向磁轴承构成的五自由度磁悬浮系统在航空高速、超高速起动/发电机领域具有广阔的应用前景。

[1] 邓智泉,严仰光.无轴承交流电动机的基本理论和研究现状[J].电工技术学报,2000,15(2): 29-35.Deng Zhiquan,Yan Yangguang.The main theory and status quo of AC bearingless motors[J].Transactions of China Electrotechnical Society,2000,15(2): 29-35.

[2] 曹鑫,邓智泉,杨刚,等.无轴承开关磁阻电机麦克斯韦应力法数学模型[J].中国电机工程学报,2009,29(3): 78-83.Cao Xin,Deng Zhiquan,Yang Gang,et al.Mathematical model of bearingless switched reluctance motors based on Maxwell stress tensor method[J].Proceedings of the CSEE,2009,29(3):78-83.

[3] 赵旭升,邓智泉,王晓琳,等.永磁偏置磁轴承的研究现状及其发展[J].电工技术学报,2009,24(9):9-20.Zhao Xusheng,Deng Zhiguan,Wang Xiaolin,et.al.Research status and development of permanent magnet biased magnetic bearings[J].Transactions of China Electrotechnical Society,2009,24(9): 9-20.

[4] 李冰,邓智泉,严仰光.一种新颖的永磁偏置三自由度电磁轴承[J].南京航空航天大学学报,2003,35(9): 81-85.Li Bing,Deng Zhiquan,Yan Yangguang.Permanent magnet biased electromagnetism bearing with three degrees of freedom [J].Journal of Nanjing University of Aeronautics and Astronautic,2003,35(9): 81-85.

[5] Zhilichev Y.Analysis of a magnetic bearing pair with a permanent magnet excitation[J].IEEE Transactions on Magnetics,2000,36(5): 3690-3692.

[6] 梅磊,邓智泉,赵旭升,等.基于磁通量计算的混合型轴向–径向磁悬浮轴承参数设计[J].中国电机工程学报,2009,29(24): 115-120.Mei Lei,Deng Zhiquan,Zhao Xusheng,et a1.Parameter design of hybrid axial-radial magnetic bearing based on magnetic flux calculation[J].Proceedings of the CSEE,2009,29(24): 115-120.

[7] Murphy Brian T,Hamid Ouroua,Matthew T,et.al.Permanent magnet bias,homopolar magnetic bearings for a 130kw-hr composite flywheel[C].Proceedings of the 9th International Symposium on Magnetic Bearings,Lexington,Kentucky,2004: 65-72.

[8] Patrick T.McMullen,Huynh Co S,et al.Combination radial-axial magnetic bearing[C].Proceedings of the 7th International Symposium on Magnetic Bearings,2000: 473-478.

[9] Huang Lei,Zhao Guangzhou,Nian Heng,et al.Modeling and design of permanent magnet biased radial-axial magnetic bearing by extended circuit theory[C].Proceedings of the International Conference on Electrical Machines and Systems,Seoul,Korea,2007: 1502-1507.

[10] Yohji Okada,Hiroaki Koyanayi,Kouichi Kakihara.New concept of miracle magnetic bearings[C].Proceedings of the 9th International Symposium on Magnetic Bearings,Lexington,Kentucky,2004:89-95.

[11] 孙津济,房建成,王曦,等.一种新型结构的永磁偏置径向磁轴承[J].电工技术学报,2009,24(11):53-60.Sun Jinji,Fang Jiancheng,Wang xi,et al.A new permanent magnet biased radial magnetic bearing[J].Transactions of China Electrotechnical Society,2009,24(11): 53-60.

[12] Martin Reisinger,Wolfgang Amrhein,Siegfried Silber,et al.Development of a low cost permanent magnet biased bearing[C].Proceedings of the 9th International Symposium on Magnetic Bearings,Lexington,Kentucky,2004: 113-118.

[13] Satoru Fukata,Kazuyuki Yutani.Characteristics of electromagnetic systems of magnetic bearings biased with permanent magnets[C].Proceedings of the 6th International Symposium on Magnetic Bearings,MIT:Technomic Publishing Co.Inc.,1998: 234-243.

[14] Fukata Satoru,Kazuyuki Yutani.Characteristics of the magnetic system of magnetic bearing biased with permanent magnets attached to a rotor[C].Proceedings of the 5th International Symposium on Magnetic Bearings,Kanazawa: Kanazawa University,1996: 395-400.

[15] Lee An Chen,Hsiao Foam Zone,KO Dennil.Analysis and testing of magnetic bearing with permanent magnets for bias[J].JSME International Journal,1994,37(4): 774-782.

[16] Eric Maslen.Magnetic Bearings [M].USA:University of Virginia,2000.