三电平双PWM变频器综合控制策略

张颖超 赵争鸣 冯 博 鲁 挺 金丽萍

（1.清华大学电机系电力系统国家重点实验室 北京 100084 2.重庆通信学院电力工程系 重庆 400035）

1 引言

相对于传统的由二极管整流器构成的交-直-交变频器，双PWM变频器具有能量双向流动、网侧电流正弦等优点，在牵引、矿井、风力发电等大功率电力电子传动场合将得到广泛的应用[1-2]。此外，与传统的两电平变换器相比，中点钳位三电平变换器由于具有独特的优势，成为高压大容量应用场合的研究热点之一[3-4]。因此，基于三电平技术的双PWM变频器不仅能够实现四象限电动机驱动，而且同时具有器件承压低、开关频率低、输出谐波小等三电平变换器的优点。

直流母线电容是影响交-直-交变频器成本、体积、可靠性的主要器件之一，而母线电压可控是双PWM变频器的优点之一。因此，如何尽可能地提高直流环节动态响应性能，以减小直流母线电容对双PWM变频器有着重要的意义。文献[5-7]将负载（电动机）侧有功电流反馈回给网侧整流器的有功电流控制环。文献[8-9]采用主-从控制的思想以维持网侧和负载侧的瞬时功率平衡。文献[10]采用直接控制电容电流的思路，将母线电容电流近似控制为零。这些方法各有其优势，也均能取得一定的效果。但总体来讲，上述方法有一个共同点，即前端的PWM整流器的控制都采用基于电压定向控制（Voltage Oriented Control，VOC）的直接电流控制策略。受控制策略本身限制，这些方法的直流环节动态性能改善余地有限。此外，上述大部分方法均是基于两电平拓扑结构的双PWM变频器。

本文提出一种新型三电平双PWM变频器综合控制方法，从两个方面提高了直流环节的动态响应。其一是前端PWM整流器采用固定开关频率直接功率控制（Direct Power Control，DPC）策略。该策略基于SVPWM，实现了固定开关频率下对网侧有功和无功功率的直接控制。此外，将逆变器-异步电动机侧的功率直接反馈给前端整流器的功率控制环，从而进一步抑制了由于电动机工作状态突变引起的母线波动。实验结果表明，新型控制策略能够有效提高系统直流环节的动态响应性能，使得进一步减小直流母线电容成为可能。

2 电路拓扑及功率平衡模型

图1给出了中点钳位三电平双PWM变频器简化电路拓扑结构，可以将其分为三个部分：网侧整流回路、直流回路及电动机侧逆变回路。

图1 三电平双PWM变频器简化拓扑Fig.1 Simplified topology of the three-level NPC based dual-PWM converter

在单位功率因数下，网侧整流回路的输入功率为

电动机侧逆变回路的输出功率为

式中ed，id——d-q坐标系下网侧电压和电流的d

轴分量；

usd，usq——d-q坐标系下电动机定子电压d、q

轴分量；

isd，isq——d-q坐标系下电动机定子电流的d、

q轴分量。

忽略开关桥路及器件损耗，可以认为

式中pcap——直流母线电容功率。

式（3）中，电动机侧逆变回路的输出功率pinv由负载的运行状态决定，prec由整流桥的控制决定。理想情况下，如果能够控制prec随pinv的变化而实时变化，则pcap为零。

3 三电平双PWM变频器控制策略

对于双PWM变频器而言，直流母线电压由前端整流器控制。因此，整流器的控制策略对直流环节的动态响应起着决定性作用。相对于传统的VOC策略，近年出现的直接功率控制（DPC）具有更好的动态性能[11-13]。此外，传统的整流-逆变独立控制下的双PWM变频器，电动机状态的突变首先引起母线电压的波动，此后整流器根据母线波动调节网侧功率。因而母线电容必须足够大以缓冲网侧整流回路和负载侧逆变回路能量分布的不平衡。而如果能将负载侧功率的变换提前反馈给整流器的功率控制环，则能有效提高系统直流环节的动态响应性能。据此，本文提出如图2所示的新型三电平双PWM变频器控制策略。

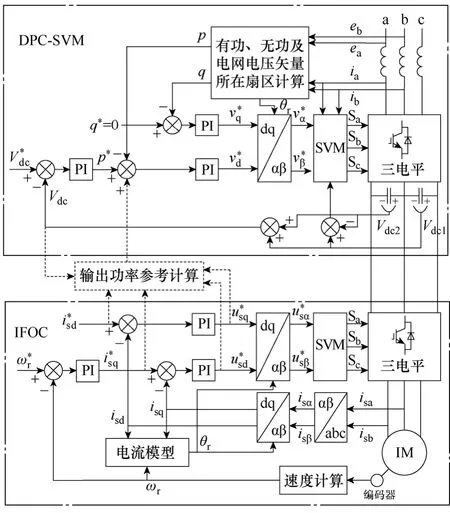
图2 三电平双PWM变频器综合控制策略Fig.2 Integrated control scheme for three-level NPC based dual-PWM converter

3.1 三电平PWM整流器DPC_SVM策略

图2 上半部分给出了三电平PWM整流器固定开关频率直接功率控制策略（DPC_SVM）。该策略基于SVPWM，和VOC不同，其内部为功率控制环，通过PI调节器实现对有功和无功功率的直接控制。采用前馈的方式能够实现有功功率和无功功率的解耦，简化的有功功率控制环如图3所示。图中Ls和Rs分别是网侧电抗器的等效电感和电阻；Ti=Kp/Ki，Kp和Ki分别是PI调节器比例和积分增益；Ts为系统采样周期；KPWM是桥路PWM等效增益。文献[14]详细介绍了DPC_SVM控制策略的原理。

图3 简化的有功功率环控制框图Fig.3 Simplified block diagram of active power control loop

3.2 三电平逆变器-异步电动机IFOC策略

三电平逆变器-异步电动机闭环控制的研究工作开展较早。本文采用如图2下半部分所示的间接磁场定向控制（IFOC）[15]。异步电动机定子电流的励磁（isd）和转矩（isq）分量分别由PI调节器构成闭环，保证了电动机良好的动、静态性能。脉宽调制同样采用三电平SVPWM策略。

3.3 输出功率反馈补偿

受功率电路响应延迟及数字控制延迟的影响，异步电动机工作状态的突变会引起母线电压的波动。为减小系统响应延迟，本文采取输出功率反馈补偿策略，如图2中虚线部分（输出功率参考计算）所示。在这种情况下，前端PWM整流器能够及时调节网侧输入功率，以提前与电动机侧逆变回路功率相匹配，避免更多的能量通过母线电容来交换，从而有效提高母线电压抗负载侧功率突变扰动的能力。下文中将详细分析该环节的补偿性能。

3.4 中点电位的平衡

中点电压的平衡是三电平拓扑在应用中必须注意的问题，否则可能导致开关器件及直流侧电容承受过高电压而损坏。基于SVM的中点平衡控制研究已有很多成果[16]。其中，通过调整具有冗余关系的小矢量来补偿中点电位偏差的方法简单有效。在三电平变换器中，具有冗余关系的小矢量对中点电位的影响是互反的。利用这一关系，通过检测交流侧电流判断出中点电流方向，并根据中点电位的偏移，在SVM中调整冗余矢量和矢量序列可有效保证中点电位的平衡。

4 功率响应延迟及母线电压波动分析

4.1 输入功率响应延迟

由图3可以得到网侧整流回路有功功率控制环的闭环传递函数为

通常控制系统的PWM采样频率较高，即Ts比较小。因此式（4）中二次项可以被忽略掉，进一步简化为一阶系统为

式中，Tdr为输入有功功率传递函数的延迟时间常数。Tdr和PI调节器比例系数Kp成反比，与交流侧电感成正比（Ti=Ls/Rs）。因此，通过增加PI调节器的比例系数Kp、减小交流侧电感量Ls，能够缩短系统延迟时间。但是，过大的Kp会导致系统的不稳定，而过小的Ls则会使网侧电流波形变差。

4.2 输出功率响应延迟

如图2所示，三电平逆变器-异步电动机IFOC控制系统内部为两个电流环分别控制定子电流的转矩和励磁分量。其d（q）轴电流环传递函数为[17]

式中Kps——d（q）轴电流环PI调节器比例增益；

L1s——定子电感；

σ——漏磁系数；

Tdi——定子电流传递函数的延迟时间常数，

同样认为PWM环节的采样频率足够高，则可以近似电压的参考值与实际值相等，即

将式（6）、式（7）代入式（2），得到

可以看出，在忽略桥路损耗的情况下，逆变器-异步电动机系统功率传递函数的延迟时间常数为Tdi。

4.3 母线电压波动分析

假设三电平双PWM变频器上下母线电压处于平衡状态，且电容容量相同。即Vdc1=Vdc2=Vdc/2，Cd1/2=Cd2/2=Cd，则

式中，Vdc（0）和Vdc（t）分别是直流母线电容初始时刻和t时刻电压值。即母线电压的波动为

假设初始时刻系统处于稳态，电容电压初始值Vdc（0）即为稳态时母线电压值，于是

代入式（10）并求平方得

相对于Vdc，ΔVdc（t）比较小，忽略其平方项，式（12）简化为

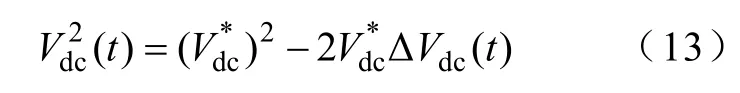
将式（13）代入式（9）并进行拉普拉斯变换得到

按照图2给出的DPC_SVM控制框图，电压外环首先采样母线电压，得到与参考电压之间的误差，用一阶惯性环节等效系统采样、保持环节，有

式中Tdc——采样环节的时间常数。

对于整流、逆变独立控制下的三电平双PWM变频器，母线电压的误差经过PI调节器直接得到输入有功功率的参考值，即

式中Kpdc，Kidc——电压环PI调节器的系数。

综合式（5）、式（8）、式（14）～式（16）可以得到在考虑采样、调节等各个环节延迟时间的情况下，母线电压波动和系统输出功率之间的传递函数结构框图如图4所示。

图4 整流、逆变独立控制下母线电压波动模型Fig.4 Model of the dc bus voltage fluctuations under individual control for rectifier and inverter

据此，得到母线电压波动和输出功率指令之间的传递函数如下：

通常在设计双PWM变频器时，可以取Tdr=Tdi，所以式（17）零极点抵消得到

从式（19）可以发现：双PWM控制系统中各个环节的采样保持、调节延迟是造成母线波动的主要原因。因此，采用如图2虚线框所示的输出功率前馈补偿方法，能够使得整流环节提前预知负载的变化，及时调整网侧整流回路的瞬态能量与负载侧瞬态能量相平衡。从而不经过直流环节或尽量减轻直流环节的调节负担。按照该方法，母线电压波动模型变化为图5所示。

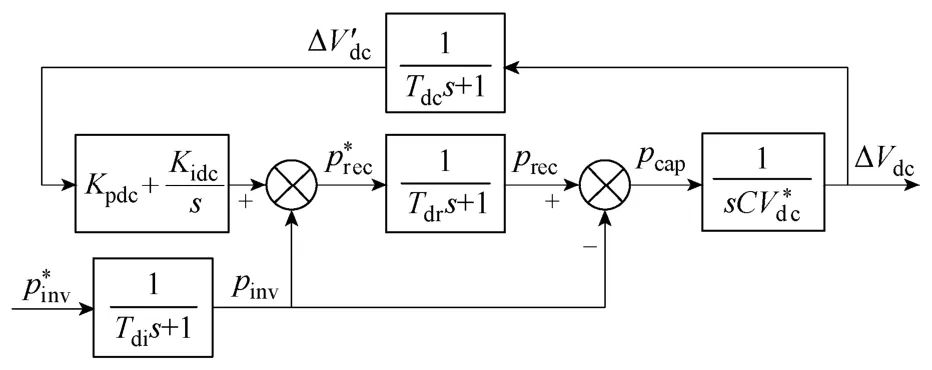
图5 整流、逆变综合控制下母线电压波动模型Fig.5 Model of the dc bus voltage fluctuations under integrated control for rectifier and inverter

进而得到其传递函数为

选择合理的控制系统参数，做出式（19）和式（20）的伯德图和冲激响应如图6所示。

图6 两种控制方式下传递函数伯德图和冲激响应Fig.6 Bode diagram of transfer functions and impulse response of the two control methods

由于电动机工作状态变化的时间尺度相对比较大，因此传递函数性能主要决定于低频段。从图6a所示的幅频曲线上可以看出，采用综合方法，系统增益明显减小，即母线电压的波动对输出功率的敏感度降低，输出功率变化引起的母线波动幅度变小。图6b为系统冲激响应曲线，冲激响应结果同样验证了上述分析的正确性。综上所述，采用综合控制策略后，能够有效抑制母线电压的波动幅度。

5 实验结果

在基于IGBT的三电平双PWM变频器实验平台上对控制策略进行了实验。变频器负载为由一异步机和直流机组成的机组，其中直流机由四象限直流调速器6RA70控制，实现能量的双向流动。控制平台以数字信号处理器（DSP）TMS320F2812和复杂可编程逻辑器件（CPLD）EPM7256为核心，完成核心控制算法以及PWM脉冲产生、死区及最小脉宽等功能。数字功率计（WT1600）、录波仪（DL750）和计算机完成数据采集分析。实验装置主要参数见下表，为考察控制算法在大容量场合下的性能，系统采样和IGBT的开关频率较低。

表 实验装置参数Tab.Parameters of experimental set-up

图7 实验结果Fig.7 Experimental results

图7 给出了系统实验结果。其中图7a为前端整流器DPC_SVM稳态实验结果。波形分别为变频器交流侧相电压va、电流ia以及整流桥交流侧线电压（vab）波形。相电压中的高次谐波是由实验系统中的调压器引起的，稳态时用横河数字功率计WT1600测试系统功率因数约为0.998。

图7b给出了后端逆变器-异步电动机IFOC实验结果。异步电动机转速由-1200r/min阶跃为零，再由零阶跃为1200r/min的情况下，逆变桥线电压（usasb）、定子电流（isa）以及电动机转速（n）的波形。

图7c、图7d给出了系统能量双向流动波形。其中图7c为电动机由电动状态突变为发电状态下网侧相电压ea、电流ia以及电动机定子电流isa的波形。异步电动机工作状态的突变通过6RA70控制直流机实现。图7d是与图7c相反的运动过程。可以看出系统实现了能量双向流动，且功率因数始终保持较好。

为全面比较综合控制策略性能，按照相同的控制参数，在同一实验装置上分别完成了三电平双PWM变频器VOC-IFOC独立控制、DPC_SVM-IFOC独立控制以及DPC_SVM-IFOC综合控制实验，三电平PWM整流器VOC控制策略可参考文献[13]。图7e、图7f及图7g给出了相应实验结果。实验中通过突然启动和断开6RA70，给变频器突加和突减约2.3kW的负载，以引起母线电压波动。其中图7e为变频器在VOC-IFOC独立控制下的实验波形，分别为网侧相电压ea，相电流ia，电动机定子电流isa以及直流母线电压Vdc。可以看出，在VOC-IFOC独立控制下，直流环节的动态响应并不理想，电动机工作状态的突变会引起母线电压的较大波动（约60V）。

图7f给出了DPC_SVM-IFOC独立控制下的实验结果。可以看出，前端整流器在DPC_SVM控制下，系统动态响应性能得到了一定程度的提高，电动机状态的突变引起约45V的母线电压波动。

图7g给出了DPC_SVM-IFOC综合控制下的实验结果。可以看出，在综合控制下，电动机状态的突变引起的母线电压波动减小为约25V。

6 结论

直流母线电容是影响双PWM变频器系统成本、体积、可靠性的主要元件，特别是在高压大容量的应用场合。本文通过采用新型三电平PWM整流器控制策略（DPC_SVM），并引入输出功率前馈补偿环节的方法，显著提高了三电平双PWM变频器直流环节的动态响应性能。理论分析和实验结果证明了该方法的有效性，直流母线电容可以得到一定程度的减小。

[1] Blaabjerg F,Pedersen J K.An integrated high power factor three-phase ac-dc-ac converter for ac-machines implemented in one microcontroller[C].Proceedings of the IEEE Power Electronics Specialists Conference,1993: 285-292.

[2] Kohlmeier H,Niermeyer O,Schraoder D F.Highly dynamic four-quadrant ac motor drive with improved power factor[J].IEEE Transactions on Industry Applications,1987,23(6): 1001-1009.

[3] Tolbert L M,Peng F Z,Habetler T G.Multilevel converters for large electric drives[J].IEEE Transactions on Industry Applications,1999,35(1): 36-44.

[4] 张海涛.基于IGCT的三电平变频器的控制系统研究[D].北京: 清华大学,2006.

[5] Wei L X,Li C J,Liu C W.A dual PWM scheme for three-level voltage source converter system with IGBT modules[C].Proceedings of the IEEE Annual Conference of the Industrial Electrionics Society,1998: 755-760.

[6] Uhrin R,Profumo F.Performance comparison of output power estimators used in ac/dc/ac converters[C].Proceedings of the IEEE Annual Conference of the Industrial Electrionics Society,1994: 344-348.

[7] Li S J,Li Y H.A novel fast current-control method for the back-to-back converters[C].Proceedings of the IEEE International Conference on Industrial Technology,2004: 351-357.

[8] Hur N,Jung J,Nam K.A fast dynamic DC-link power-balancing scheme for a PWM converterinverter system[J].IEEE Transactions on Industrial Electronics,2001,48(4): 794-803.

[9] 王锋,姜建国.风力发电用双PWM变换器的功率平衡联合控制策略研究[J].中国电机工程学报,2006,26(22): 134-139.Wang Feng,Jiang Jianguo.Research of powerbalancing combined control scheme for back to back PWM converters used in wind generator[J].Proceedings of the CSEE,2006,26(22): 134-139.

[10] Gu B G,Nam K.A DC-link capacitor minimization method through direct capacitor current control[J].IEEE Transactions on Industry Applications,2006,42(2): 573-581.

[11] Malinowski M,Kazmierkowski M P.A comparative study of control techniques for PWM rectifier in AC adjustable speed drives[J].IEEE Transactions on Power Electronics,2003,18(6): 1390-1396.

[12] Zhang Y C,Zhao Z M,Eltawil M,et al.Performance evaluation of three control strategies for three-level neutral point clamped PWM rectifier[C].Proceedings of the IEEE Applied Power Electronics Conference,2008: 259-264.

[13] 伍小杰,罗悦华.三相电压型PWM整流器控制技术综述[J].电工技术学报,2005,20 (12): 7-11.Wu Xiaojie,Luo Yuehua.A control technical summary of three-phase voltage-source PWM rectifiers[J].Transactions of China Electrotechnical Society,2005,20(12): 7-11.

[14] 张颖超,赵争鸣,鲁挺,等.固定开关频率三电平PWM整流器直接功率控制[J].电工技术学报,2008,23(6): 72-76.Zhang Yingchao,Zhao Zhengming,Lu Ting,et al.Direct power control with constant switching frequency for three-level PWM rectifier[J].Transactions of China Electrotechnical Society,2008,23(6): 72-76.

[15] Bose B K.Modern power electronics and AC drives[M].Beijing: China Machine Press,2006.

[16] Celanovic N,Boroyevich D.A comprehensive study of neutral-point voltage balancing problem in threelevel neutral-point-clamped voltage source PWM inverters[J].IEEE Transactions on Power Electronics,2000,15(3): 242-249.

[17] 杨耕,罗应立.电动机与运动控制系统[M].北京:清华大学出版社,2006.