镍基粉末高温合金FGH98流变曲线特性及本构方程

刘 洋，陶 宇，贾 建

(钢铁研究总院高温材料研究所，北京 100081）

镍基粉末高温合金FGH98流变曲线特性及本构方程

刘 洋，陶 宇，贾 建

(钢铁研究总院高温材料研究所，北京 100081）

通过对第三代镍基粉末高温合金FGH98进行热模拟压缩实验，得到了不同温度(1050～1110℃）和不同应变速率下(0.01～1s－1）的真应力-真应变曲线。根据其特点分析了该合金的流变应力与温度和应变速率以及应变量的关系。由实验结果得出:该曲线呈典型的热激活特征，合金流变应力对变形温度和应变速率敏感。在此基础上选用Arrhenius方程低应力水平下的简化模型作为其本构关系的经验公式，利用线性回归法确定相关系数并对其误差进行分析，从而得到了该合金的本构方程。

FGH98;粉末冶金;高温合金;真应力-应变曲线;线性回归;本构方程

第三代镍基粉末冶金高温合金，兼具第一代粉末高温合金的高强度和第二代粉末高温合金的损伤容限设计的优点，是新一代航空发动机热端部件的首选材料［1，2］。FGH98合金是钢铁研究总院自主研发的第三代镍基粉末冶金高温合金，具有优越的高温力学性能，可用于高推重比航空发动机。研究表明，对粉末冶金高温合金实施热加工变形，能够起到成形和改性的双重效果［3］。通过对HIP态的FGH98实验锭坯实施等温锻造，不仅可以实现近终成形，而且可以改善组织，提高性能。

本工作通过对FGH98合金进行热模拟压缩实验，得到了 1050～1110℃，0.01～1s－1，不同温度和不同应变速率下材料的真应力-真应变关系曲线。通过分析曲线特征，选择适合的经验方程作为材料本构关系模型。关于镍基粉末高温合金的本构关系的研究，已有相关的文献发表，但大多数为普适型的本构关系［4］。针对第三代镍基粉末冶金高温合金FGH98晶粒比较细小，在高温下加工应力水平较低的特点，选择Arrhenius双曲正弦方程低应力水平下的简化模型作为经验方程，具体分析了流变应力对应变速率、温度、应变的依赖关系，确定相关参数，并根据Zener因子值和实际金相观察结果，分析了热加工参数温度和应变速率对FGH98合金材料热变形过程中组织变化的影响。

1 实验材料及方法

实验采用的第三代镍基粉末高温合金FGH98，其成分为(质量分数/%）:C 0.053，Cr 12.27，Co 20.64，Mo 3.86，W 2.10，Al 3.46，Ti 3.70，Nb 0.9，Ta 2.38，B 0.023，Zr 0.049，Ni余量。实验锭坯制备工艺:母合金熔炼(VIM）+旋转电极制粉(PREP）+热等静压成形(HIP）。实验锭中心区取样，制成规格为φ8mm×12mm圆柱形试样，试样两端用石墨片润滑。在Gleeble-1500D热模拟试验机上对试样进行了五个温度 (1050℃，1065℃，1080℃，1095℃，1110℃）和五个应变速率(0.01，0.05，0.1，0.5，1）的热模拟压缩实验。用Origin7.0数据分析软件对实验数据进行了处理。

2 实验结果和分析

2.1 流变曲线特征

图1显示了FGH98合金的流变应力曲线随着变形量的增加，流变应力迅速达到峰值，然后保持不变或逐渐下降，最终曲线呈现稳态流变特征。合金的变形可分为三个阶段:第一阶段随着变形量的增加，流变应力迅速增大;第二阶段软化机制开始作用，流变应力增速趋缓;第三阶段，流变应力值开始减少，曲线下降，一直到动态再结晶结束，软化速率与加工硬化速率才达到平衡，流变应力此时趋于稳定;如果没有发生动态再结晶，流变应力达到峰值后保持不变或略有下降，流变曲线与横坐标轴基本上保持平行，呈现典型的动态回复的流变曲线特征。

FGH98合金的流变应力对于温度和速率都非常敏感，在同一应变量下，温度一定，应变速率越大，流变应力越大;应变速率一定，温度越高，流变应力越小，软化机制发挥作用。在1050℃和1065℃，流变曲线在达到峰值后减少的幅度较大，材料呈现出典型的动态再结晶特征;而在1095℃和1100℃，除了个别应变速率较高(0.5s－1，1s－1）的曲线外，流变应力在达到峰值后，下降较缓或保持稳定值，这是典型的动态回复的特征。

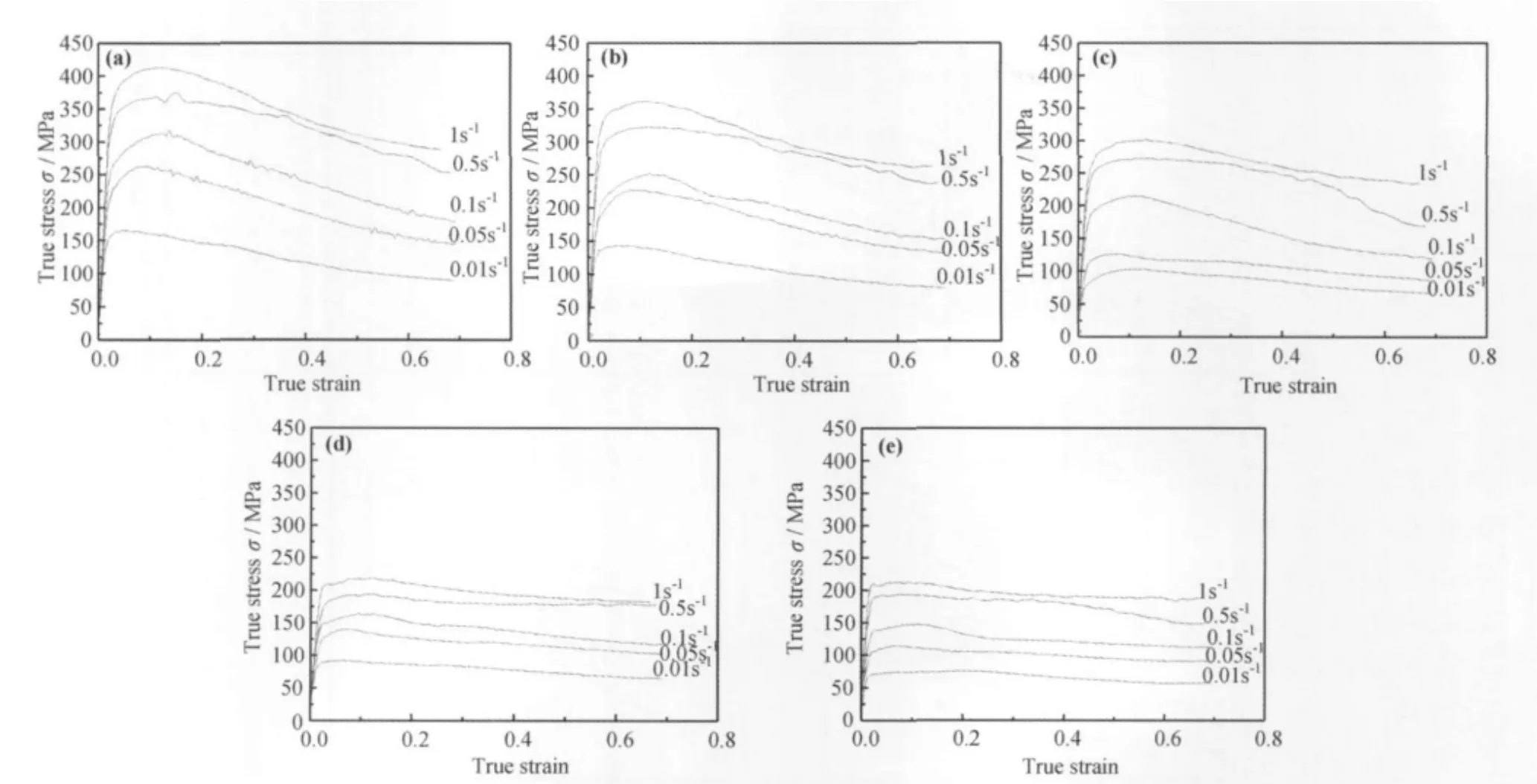
图1 FGH98在不同温度和应变速率下的真应力-真应变曲线Fig.1 True stress-true strain curves of FGH98 at different strain and temperature(a）1050℃;(b）1065℃;(c）1080℃;(d）1095℃;(e）1110℃

2.2 经验方程

根据本构方程的定义，高温变形时材料的本构方程可以表示成:

式中T为温度，˙ε为应变速率，ε为应变量。由图1可知，一定应变量下材料流变应力σ与温度T，应变速率˙ε的函数关系可满足Arrhenius双曲正弦方程［5～7］:

式中的A，n，α均为与温度无关的常数;R为气体常数，取值8.314J/(mol·kg）;T为绝对温度;Q为变形激活能。根据本研究实验数据计算可知，对于FGH98合金 ασ最大值为0.27，符合低应力水平(ασ ＜0.8）特点，因此式(2）可以简化如下［8］:

本工作采用方程(3）作为本构方程模型进行分析。

2.3 应变速率对流变应力的影响

将式(3）变形为:

从式(4）可以看出，当温度T一定时，应力自然对数lnσ与应变速率自然对数ln˙ε呈线形关系。用最小二乘法对实验数据进行拟合后，得到一系列线形相关系数非常高(R＞0.98）的直线方程。应变ε一定时，各个温度下拟合的直线几乎平行，如图2所示。各应变下的斜率(1/n）如表1所示。由此可知n值是一个与应变ε相关的量。

表1 各应变量(ε）下线形拟合斜率1/n，Q/Rn×10－4值Table 1 The values of 1/n，Q/Rn ×10 －4at each strain

2.4 变形温度对流变应力的影响

由式(4）可得，当应变速率˙ε一定时，应力自然对数lnσ与温度1/T也为线形关系。按照同样的处理方法可得到应变ε一定时，不同应变速率下的直线方程构成的平行直线系，如图3所示。各应变量下所得斜率(Q/Rn×10－4）如表1所示。由此可以计算出Q值，可知热激活能Q的大小也与应变ε相关。

图2 FGH98合金流变应力与速率在不同应变量(ε）下自然对数关系Fig.2Relations of lnσ with ln˙ε at different strains ε(a）0.1;(b）0.15;(c）0.2;(d）0.3;(e）0.4;(f）0.5;(g）0.6

2.5 温度补偿速率因子Z

综合考虑应变速率˙ε和温度T对流变应力的影响，根据Zener-Hollomon因子:

将式(5）变形为:

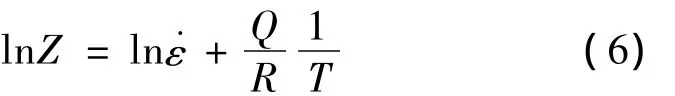
从式(5），(6）可以看出Z，lnZ值随着˙ε值增大而增大，随着T值增大而减小。所以当T越低，˙ε越大时，Z值也越大。根据表1和相关的T，˙ε值，很容易计算得到lnZ。从表1中可以看出，激活能Q是一个与应变量ε相关的量。联系图1分析可知，在ε=0.15时，即材料发生动态再结晶的临界应变附近，Q值最大，随着ε的增加动态再结晶和动态回复等软化机制逐渐占据优势，Q值减少。从式(8）可知，当T，˙ε一定时，lnZ的变化趋势与Q基本保持一致。根据计算结果可以作出ε=0.15处lnZ与lnT，ln˙ε的三维函数曲面和关于lnZ的等高线图，如图4所示。从图4可以看出lnZ随T，˙ε变化趋势与前面分析一致。

依据图1和图4以及式(5），(6）分析可得:Z值的大小反映再结晶的难易程度，当Z值变大时，意味着发生再结晶时临界应变值(一般近似地用峰值应变εp表示）和峰值应力σp相应的增大，也就是说需要更大的应力和变形量才能使材料发生动态再结晶，这在温度较低时，如1050℃和1065℃尤为明显，高温下峰值应变量变化不明显。同时Z值也是控制材料变形组织的一个重要参考量。相关文献和实验表明在满足发生动态再结晶所需的临界应变和临界应力值条件的前提下，Z值越大，变形所得的动态再结晶平均晶粒尺寸越小。也就是说较低的温度和较高的应变速率下的热变形细化晶粒的作用非常明显。

图5 FGH98合金经不同热变形工艺后的回复和再结晶组织Fig.5 Microstructure of dynamic recrystallization(DRX）and dynamic recovery(DRV）of FGH98 after different hot processing treatment(a），(b）DRX，T=1050℃，˙ε=1s－1;(c），(d）DRV，T=1110℃，˙ε=0.01s－1

从图5a，5b可以看出，当T=1050℃，˙ε=1s－1，材料发生了完全动态再结晶，此时Z值较大，晶粒非常细小，平均晶粒尺寸约为5μm;当T=1110℃，˙ε=0.01s－1时，在此高温低速的变形条件下，材料软化以动态回复为主，如图5c，5d。此时原始晶粒沿流变方向被拉长，其内部形成亚晶组织。

2.6 本构方程的确定

根据上述的拟合结果可以分别计算出各个应变量下 n，Q，lnA 的值，见表2。

表2 各应变量(ε）下n，Q，lnA值Table 2 The values of n，Q，lnA at each strain

从表2可以看到，本构方程系数n，Q，lnA随着应变量ε值的变化而呈一定规律性的变化。定义函数 n(ε），Q(ε），ln(A(ε））。将表2 的数据导入 Origin软件中，分别作出n，Q，lnA散点分布图，如图3所示。

根据系数n，Q，lnA离散点的分布特点，用线形回归法拟合函数 n(ε），Q(ε），ln(A(ε））得到如图6a～c所示直线关系。其线形相关系数分别为:R1= － 0.99436，R2= －0.98842，R3= －0.98989。根据拟合的结果，本构方程式(4）可以写成:

对实验结果进行验证。为了计算方便，可以先由式(5）计算得到各个应变处的 lnσ值(Calc.lnσ），与相应的lnσ实验值(Reallnσ）比较，计算出绝对误差。表3是ε=0.1时，lnσ的计算值和实验值以及绝对误差。由表3得出，当ε=0.1时，lnσ的绝对误差平均值为0.124211。

图6 FGH98合金材料参数n，Q，lnA与应变量ε的关系Fig.6 Relations between material parameters n，Q，lnA and the strains ε for alloy FGH98(a）n-ε ;(b）Q-ε ;(c）lnA-ε

表3 ε=0.1时，lnσ的绝对误差值Table 3 The values of absolute error of lnσ at ε =0.1

3 结论

(1）FGH98材料热模拟压缩实验的流变应力曲线呈典型的热激活特征。从曲线上可以看到，随着应变量的增加，材料依次经历加工硬化阶段、软化阶段、软化机制与加工硬化趋于平衡阶段。该材料对温度和应变速率敏感，在同一应变下，温度一定，应变速率越大，流变应力越大;应变速率一定，温度越高，流变应力越小。

(2）对实验数据进行回归分析得到:各应变下，当温度T一定时，应力自然对数lnσ与应变速率自然对数ln˙ε呈线形关系，当应变速率˙ε一定时，lnσ与温度1/T也为线形关系。

(3）由实验数据和计算结果可知，流变应力σ是一个与应变量ε相关的量。根据拟合结果，得到流变方程为:

［1］胡本芙，刘国权，贾成厂，等.新型高性能粉末高温合金的研究与发展［J］.材料工程，2007(2）:49－57.

［2］贾建，陶宇，张义文，等.第三代粉末冶金高温合金René104的研究进展［J］.粉末冶金工业，2007，6:36 －43.

［3］李力，杨士仲，强劲熙.热等静压及其加锻造和热挤压粉末高温合金FGH95的组织和性能［J］.钢铁研究总院学报，1985，5(4）:411 －415.

［4］吴凯，刘国权，胡本芙，等.新型镍基粉末高温合金的高温变形行为［J］.航空材料学报，2010，30(4）:1－7.

［5］王少林，阮雪榆，俞新陆，等.金属高温塑性本构方程的研究［J］.上海交通大学学报，1985，5(4）:20－24.

［6］张仁鹏.含夹杂粉末高温合金等温预成形设计与过程模拟［D］.西安:西北工业大学，2007:24－25.

［7］LENARD G J G.Modelling hot deformation of steels［M］.Berlin:Springer-Verlag，1989:101 －115

［8］PETER T，TANEV J.A neutral templating route to mesoporous molecular［J］.Science，1995，267(10）:865 －867.

Characteristics of Flow Curves and Constitutive Equation of Nickel-Based P/M Superalloy FGH98

LIU Yang， TAO Yu， JIA Jian
(High Temperature Materials Research Institute，Central Iron and Steel Research Institute，Beijing100081，China）

Based on the data of hot-compressing tests which were carried out at temperature ranged from 1050℃ to 1110℃ and strain rate from 0.01s－1to 1s－1，a system of flow curves of the new type 3rdgeneration nickel-based superalloy FGH98 was obtained .Then they were used to uncover how the flow stress changes by the change of temperature and strain rate as well as strain.It shows that the curve takes on a typical agitation charateristic and the flow stresses are very sensitive to temperature and strain rate.Subsequently，Arrehenius equation was selected as a model of the constitutive relationship，and the relative parameters were figured out by linear regression analysis of the experimental data with simple error analysis.Then the constitutive equation has been established.

FGH98;P/M superalloy;true stress-true strain curve;linear regression model;constitutive equation

10.3969/j.issn.1005-5053.2011.6.003

V223;V215.5

A

1005-5053(2011）06-0012-07

2011-01-20;

2011-04-15

国家高技术发展计划(2007AA03A223）

刘洋(1984—），男，硕士研究生，主要从事粉末冶金高温合金方面的研究，(E-mail）ly_0734@163.com。