一类局域共振型声子晶体梁的带隙分析

舒海生，张法，余豪华，刘少刚

(哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001)

声子晶体通过周期性地改变材料参数和(或)结构型式，能够产生不同中心频率和带宽的弹性波禁带(band gap).根据禁带形成机理的不同，声子晶体可以分为两大类:布拉格散射型［1-3］和局域共振型［4-8］.布拉格散射型声子晶体的禁带来源于结构或材料对弹性波的严格的周期性调制作用，因此对周期性要求很严，并且所产生的禁带中心频率较高(几kHz至上百kHz)，这也极大地限制了其在工程上的应用范围.局域共振型声子晶体自从2000年刘正猷教授提出以来，由于它能产生低频禁带(几十Hz至几百Hz)，可以实现“小尺寸控制大波长”，因而越来越受到研究人员的重视，针对局域共振型声子晶体的研究也越来越深入.文献［7，9］针对一维杆、梁、轴和二维声子晶体板等工程应用较广泛的结构进行深入研究，并得到了一些有价值的结果.其中对于一维声子晶体梁的弯曲振动带隙，分别采用单自由度和双自由度模型进行分析，得到较为理想的低频禁带，并指出该禁带的起始频率由局域共振子的横向振动模式决定，相邻振子间保持反相关系，而截止频率则由该振子与基体梁的反相位横向共振模式决定，相邻振子间呈现同相关系.

本文针对一类由环氧树脂为基体，其上安装硫化橡胶套和铅套，从而构成的声子晶体自由梁进行分析，有限元计算结果显示出了一些不同于以往研究的现象，结合现有的局域共振原理加以分析比较，获得了一些有意义的结果.

1 声子晶体梁模型及局域振子固有频率

所研究的一维三组元梁模型如图1(a)所示，图1(b)给出了该声子晶体梁的单个元胞结构，铅套通过硫化橡胶套与树脂梁粘接在一起.分析计算中各参数分别取如下数值:

环氧树脂:密度1 180 kg/m3，杨氏模量0.435 ×1010Pa，泊松比0.367 9.

硫化橡胶:密度1 300 kg/m3，杨氏模量1×106Pa;泊松比0.470 6.

铅:密度 11 600 kg/m3，杨氏模量4.08 ×10-10Pa，泊松比0.369 1.

结构参数:r1=5 mm，r2=8 mm，r3=10 mm，h=25 mm，梁长L=75 mm，局域振子位于梁的正中.

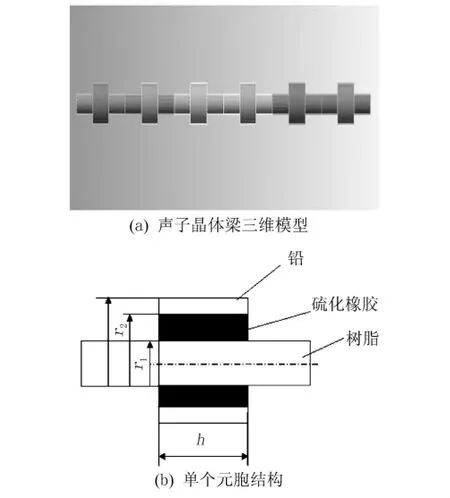
图1 声子晶体梁结构Fig.1 Structure of phononic crystal beam

依据现有的局域共振型声子晶体禁带形成机理［9］，该声子晶体梁应该存在低频禁带，并且第一带隙的起止频率应与局域振子的共振模式密切相关.因此，首先对该局域振子的固有频率和固有振型的进行分析，以便后续分析和讨论.

在简化分析中可将该局域振子视为二自由度弹簧振子模型，振子质量即为铅套质量，刚度则由硫化橡胶提供.由于该模型关于铅环质心左右对称，因而质心横向振动和绕质心的摆动是解耦的，低频横向振动时橡胶环刚度k可按下式计算:

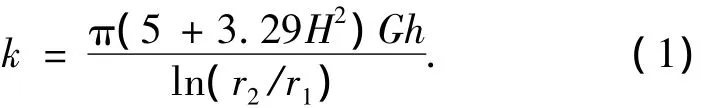
式中:G为剪切弹性模量，H为形状系数，且有

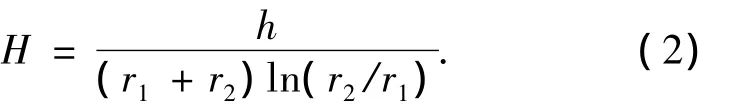
若将上述的k值和铅环的质量m代入横向固有频率f1的一般计算式中，则有

显然，由于该固有频率很高，因此按上式计算已不具有实际意义，橡胶套分布质量将对实际的横向固有频率有较大影响，从后面的数值分析不难发现实际的f1远低于1 624Hz.

摆动固有频率的计算需要确定铅套的绕质心的转动惯量J以及橡胶套提供的摆动刚度K.其中，绕质心的转动惯量J为

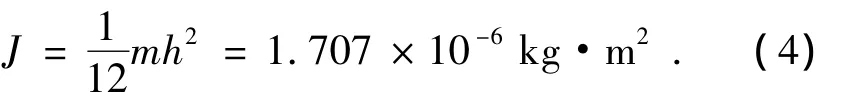
而摆动刚度K的计算可以按如下方法进行，如图2所示，首先针对每个宽度为du的橡胶环微元，按式(1)和(2)计算其微刚度dk，并忽略二阶微量可得

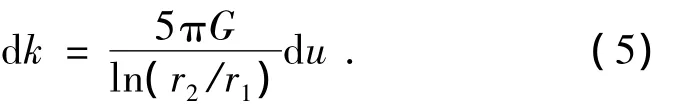
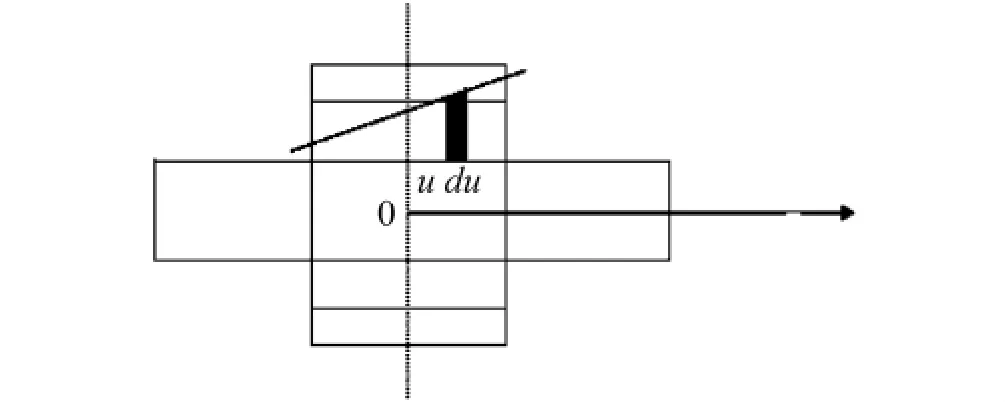
图2 摆动刚度计算简图Fig.2 Calculation diagram for swing stiffness

根据摆动刚度的定义，即

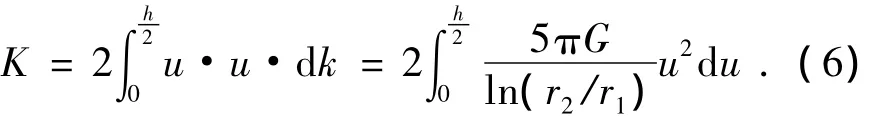
代入相关参数即可得到 K为14.79 N·m/rad.因此，摆动固有频率f2为

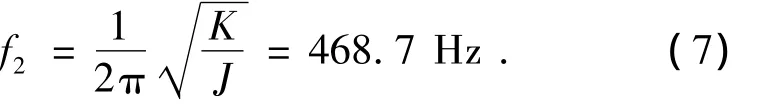
与f1相比，f2的数值是相对准确可信的，一方面由于该频率值较低，分布质量的波效应还不明显;另一方面从摆动模式不难看出，距离铅环质心较远处的橡胶环微元更多地参与了摆动运动，而距离质心较近的微元参与程度较低，因此总体上能够影响到摆动频率的分布质量也远少于横向振动模式.为精确计算f1和验证f2，在有限元分析软件 Ansys Workbench中进行了单个局域振子的模态分析.分析结果给出了前10阶固有频率如表1所示.

表1 局域振子前10阶固有频率Table 1 The first ten bands of natural frequencies for local oscillator

图3 局域振子的部分振型Fig.3 Part of the vibration mode of local oscillator

第1阶振型为径向胀缩，第2阶为轴向伸缩，第7阶以后的振型则为硫化橡胶内部的共振模式，这些振动模式均不能与基体梁中的弯曲波发生耦合，因此不具体分析.第3、4阶固有振型是摆动振型(互为正交方向)，频率在474 Hz附近，与前文理论计算得到的f1是相符的，表明简化分析对于摆动模式是可行的.第5、6阶固有振型为横向振动，固有频率在698 Hz附近，远远低于按简化模型计算的f1值，这也表明了简化分析对于此处的横向振动是不适用的，橡胶的分布质量影响不可忽略.图3给出了第3～6阶振型，图3(a)为局域振子的纯摆动模态，而图3(b)为局域振子的纯横向振动模态.

2 声子晶体梁的振动传输特性计算

在三维建模软件Proe Wildfire4.0中建立自由梁装配模型，通过 IGES中性文件导入到 Ansys Workbench中进行接触关系调整和网格划分，然后进行谐响应分析，横向位移加载在梁的一端，并在另一端拾取位移响应，最终生成振动传输特性曲线.分别针对6周期和10周期的梁模型进行分析计算，生成的频响曲线如图4所示.结果表明该梁在0～2 500 Hz存在一个很宽的振动传输衰减区，即460～2 220 Hz这个带隙，衰减十分显著，其中6周期梁可达-70 dB，而10周期梁可达-90 dB(未计阻尼).此外，在该带隙中的1 480 Hz附近存在一个较强的共振峰，在该频率附近的衰减很小.

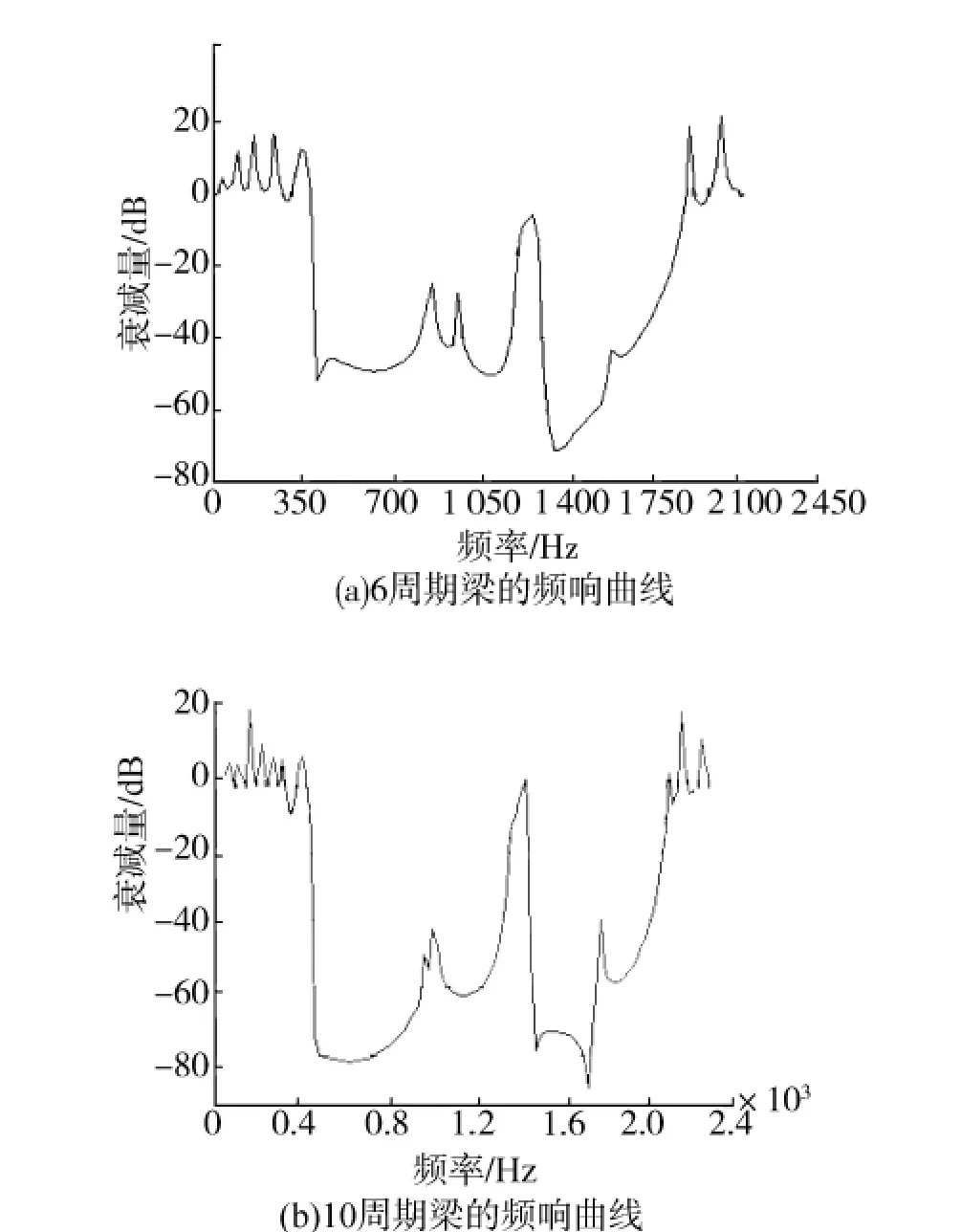
图4 声子晶体梁弯曲振动频响函数曲线Fig.4 Function curves of bending vibration frequency response for phononic crystal beam

3 带隙及其振动模式分析

在带隙的起始频率460 Hz处，局域振子和基体梁的振动模式如图5和6所示.

图5和6表明，带隙起始频率处的基体梁基本不动，振动主要局限在局域振子中，符合局域共振型带隙发生机理.与以往研究［4，9］不同的是，此处振子的振动型式为摆动模式，且该起始频率与局域振子摆动固有频率一致.表明除了振子的横向振动模式可以与基体梁中的弯曲波发生耦合从而产生带隙［4］之外，该局域振子的摆动模式也能够与基体梁中的弯曲波发生有效地耦合，进而产生带隙，并且这种摆动模式与弯曲波的耦合是该带隙起始频率的决定因素，可以运用前文所述的计算摆动固有频率的简化模型来计算该声子晶体梁的带隙起始位置.此外，从局域振子的横向振动固有频率与摆动固有频率对比也不难发现，该局域振子f2的低于f1，因而在摆动模式与梁弯曲波的耦合作用下，带隙得以首先在附近形成.

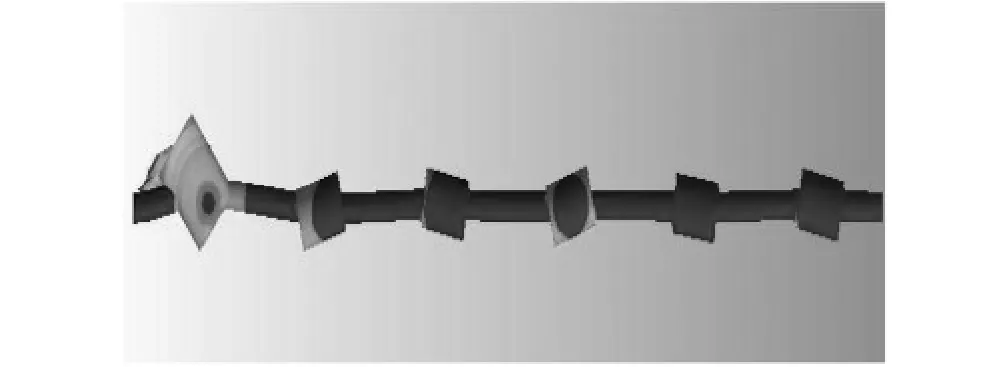
图5 6周期梁带隙起始频率处的振动模式(460 Hz)Fig.5 6 cycles of beam vibration gap in start frequency for vibration mode(460 Hz)

图6 10周期梁带隙起始频率处的振动模式(460 Hz)Fig.6 10 cycles of beam vibration gap in start frequency for vibration mode(460 Hz)

在相位关系上，在由振子摆动模式形成的耦合情况下，相邻振子间不再是简单的反相关系，而是呈现出一定的随机性，不具有明显的规律性，例如6周期梁与10周期梁的相位关系即为完全不同的2种分布类型.不同相位关系能够产生同一频率位置的带隙现象初步表明了局域振子的摆动模式与基体梁弯曲波的耦合可以以不同的相位形式发生，这与横向振动模式所导致的耦合情况有很大的不同.

在截止频率处，声子晶体梁的振动模式如图7和8所示.局域振子振动较小，振动主要集中在基体梁中.基体梁与振子为反相位横向振动，但这种横向振动与以往研究［4，9］在振动型式和相位关系存在明显不同.振动型式上基体梁主要为弯曲振动，每个元胞内的弯曲情况相同，且在元胞两端处十分类似于铰支边界;相位关系上，相邻元胞的相位始终保持反相.

根据截止频率处基体梁和局域振子的耦合振动模式，针对单个元胞建立了两端中心铰支的计算模型并进行有限元模态分析，结果表明该元胞在2 197.6 Hz和2 199.5 Hz处存在如图9 所示的耦合振动模态，该模态振型与声子晶体梁在截止频率数值上以及振动形态上是十分相符的，表明所分析的声子晶体梁的带隙截止频率是由梁与振子的反相位横向弯曲振动模式决定，可以采用两端中心铰支的元胞简化模型计算该截止频率值.

图7 6周期梁带隙截止频率处的振动模式(2 220 Hz)Fig.7 6 cycles of beam vibration gap in stop frequency for vibration mode(2 220 Hz)

图8 10周期梁带隙截止频率处的振动模式(2 220 Hz)Fig.8 10 cycles of beam vibration gap in stop frequency for vibration mode(2 220 Hz)

图9 单个元胞两端中心铰支时的固有振型(2 197.6 Hz和2 199.5 Hz)Fig.9 Natural vibration mode of the single cell with two ends in central hinging(2 197.6 Hz and 2 199.5 Hz)

4 结论

通过对6周期和10周期声子晶体梁的带隙和相应的振动模式的分析可以得出以下结论:

1)该局域共振型声子晶体梁结构在0～2 500 Hz范围内存在一个很宽的带隙460～2 220 Hz，衰减较强，具有较好的弯曲振动宽频减振性能;但在1 480 Hz附近具有较强的共振峰，减振效果将受到较大影响.

2)带隙起始频率由局域振子的摆动模式固有频率决定;基体梁振动很小，振动局域在振子中;相邻振子间的相位关系呈现出一定的随机性，不具有明显的规律性;局域振子的摆动固有频率简化计算模型能够较准确地计算带隙的起始频率.

3)带隙截止频率处的振动模式为基体和振子间的反相位横向弯曲振动，其中振子振动较小而基体振动明显;相邻元胞间的振动相位相反;两端中心铰支的单个元胞计算模型能够较准确地计算带隙的截止频率.

［1］LAI Yun，ZHANG Zhaoqing.Large band gaps in elastic phononic crystals with air inclusions［J］.Applied Physics Letters，2003，83(19):3900-3902.

［2］郁殿龙，温激鸿，刘耀宗.充液周期管路的轴向振动带隙特性［J］.机械工程学报，2009，45(9):36-41.

YU Dianlong，WEN Jihong，LIU Yaozong.Axial vibration property of periodic pipe system conveying fluid［J］.Journal of Mechanical Engineering，2009，45(9):36-41.

［3］PAROBAS I E，SIGALAS M M.Elastic band gaps in a FCC lattice of mercury spheres in aluminum［J］.Phys Rev B，2002，66(5):052302.1-052302.3.

［4］郁殿龙.基于声子晶体理论的梁板类周期结构振动特性研究［D］.长沙:国防科技大学，2006:66-74.

YU Dianlong.Research on the vibration rand gaps of periodic beams and plates based on the theory of phononic crystals［D］.Changsha:Natinal University of Defense Technology，2006:66-74.

［5］LIU Z Y，CHAN C T ，SHENG P.Analytic model of phononic crystals with local resonances［J］.Phy Rev B，2005，71(1):014103.1-014103.8.

［6］GOFFAUX C，SANCHEZ D J.Two-dimensional phononic crystals studied using a variational method:application to lattices of locally resonant materials［J］.Phys Rev B，2003，67(14):144301.1-144301.10.

［7］王刚.声子晶体局域共振带隙机理及减振特性研究［D］.长沙:国防科技大学，2005:10-13.

WANG Gang.Research on the mechanism and the vibration attenuation characteristic of locally resonant band gap in phononic crystals［D］.Changsha:Natinal University of Defense Technology，2005:10-13.

［8］WANG Gang，WEN Xisen，WEN Jihong，LIU Yaozong.Quasi one-dimensional periodic structure with locally resonant band gap［J］.ASME Journal of Applied Mechanics，2006，73(1):167-169.

［9］温熙森，温激鸿，郁殿龙，等.声子晶体［M］.北京:国防工业出版社，2009:146-178.

WEN Xiseng，WEN Jihong，YU Dianlong.et al.Phononic crystals［M］.Beijing:National Defence Industry Press，2009:146-178.

［10］赵存生，朱石坚.橡胶金属环静刚度特性研究［J］.中国机械工程，2004，15(11):962-964.

ZHAO Cunsheng，ZHU Shijian.Study on the static stiffness characteristics of rubber:metal ring［J］.Chinese Mechanical Engineering，2004，15(11):962-964.