MWEDM表面三维粗糙度的小波评定基准面

张志航，崔海，丁海娟，2，郭黎滨

(1.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001;2.佳木斯大学 机械工程学院，黑龙江 佳木斯 154007)

随着精密机械、微机电系统的深入发展和广泛应用，微细电火花线切割加工(micro wire wlectrical discharge machining，MWEDM)越来越受到人们的重视［1-2］.微细电火花线切割以其较高的加工精度、加工效率和性价比加工微小复杂的三维零件，已经成为微细加工领域重要的加工方法［3］.

由于微机械构件特征尺寸很小，在工作过程中表面粗糙度对其使用性能和工作精度的影响不容忽视［4］.表面微观形貌的精确测量和合理表征就显得尤为重要，传统的二维表征在不同表面形貌特征的识别和表面性能的描述上有很大的不足，三维表征包含表面更为丰富的信息，能够全面描述表面微观形貌特征及性能.三维表面粗糙度提取的核心在于确定评定基准［5］.到目前为止，提取基准面的常用方法有多项式拟合法和滤波法.

多项式拟合法对二维曲线较为实用，但不便推广到三维表面.滤波法理论上可以较准确的提取基准面，工程人员先后提出了数十种不同的滤波方法来分离和提取基准面与粗糙度特征，但都存在不足之处［6］.小波滤波克服了传统滤波方法的缺陷，可以实现表面的多尺度分析，但最优小波基的选取和小波分解次数的确定一直是表面分析中的难点而没有得到很好的解决.在实际应用中，这2个问题都由使用者的经验决定.

本文将小波变换应用于微细电火花线切割加工表面三维粗糙度分析，提出了最优小波基的选择原则和小波基准面分解次数的确定方法.

1 微细电火花线切割表面三维特征

微细电火花线切割加工时由于运丝机构的振动、电极丝的往复运动、火花放电时的爆炸蚀除与冲击等，其加工表面微观形貌是由近似椭球形的凹坑和凸峰组成.如图1所示.

图1 微细电火花线切割加工表面微观三维形貌Fig.1 The 3D surface micro-topography of MWEDM

因此，表面包括粗糙度、表面波纹度、几何形状误差，同时其纹理没有切削加工的方向性，是近似符合高斯分布的各向同性表面.其中表面波纹度和几何形状误差二者的叠加即为表面三维粗糙度的评定基准面.评定三维粗糙度时，要将其分离.

小波变换能将原始信号分解为不同尺度空间的基本成分组，在不同尺度上分离和提取各种表面元素，基于小波变换将尺度空间上的不同成分分离再极好地重构，具有良好的时频局域化性能.正交小波具有极好的去相关性，这对微细电火花线切割表面三维粗糙度与基准面的分离相对其他滤波方法有无可比拟的优点.

2 基准面的数学模型及其小波实现

2.1 数学模型

微细电火花线切割表面微观形貌是表面粗糙度、表面波纹度、几何形状误差和表面纹理等多种成分的总合.作为信号，以上各种成分的频率特征是不同的，粗糙度属于高频信号，相对而言，波纹度、几何形状误差和纹理属于低频信号.

记SPM显微镜扫描的微细电火花线切割加工表面微观三维形貌为 f(x，y)，s(x，y)是表面粗糙度，g(x，y)是表面波纹度、几何形状误差的总和，也就是粗糙度评定的基准面.则微细电火花线切割表面三维形貌粗糙度评定的数学模型为

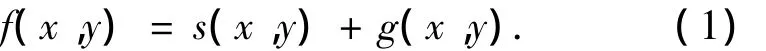
设二维正交小波基 ψ(x，y)，φ(x，y)= φ(x)·φ(y)是相应的二维尺度函数.对于微细电火花线切割加工表面微观三维形貌 f(x，y)，其逼近图像Ajf(x，y)的二维 Mallat分解算法［7-8］为

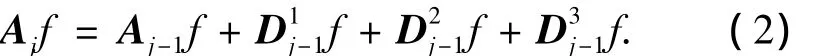
其中:

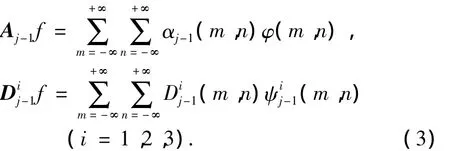
式(2)、(3)中:

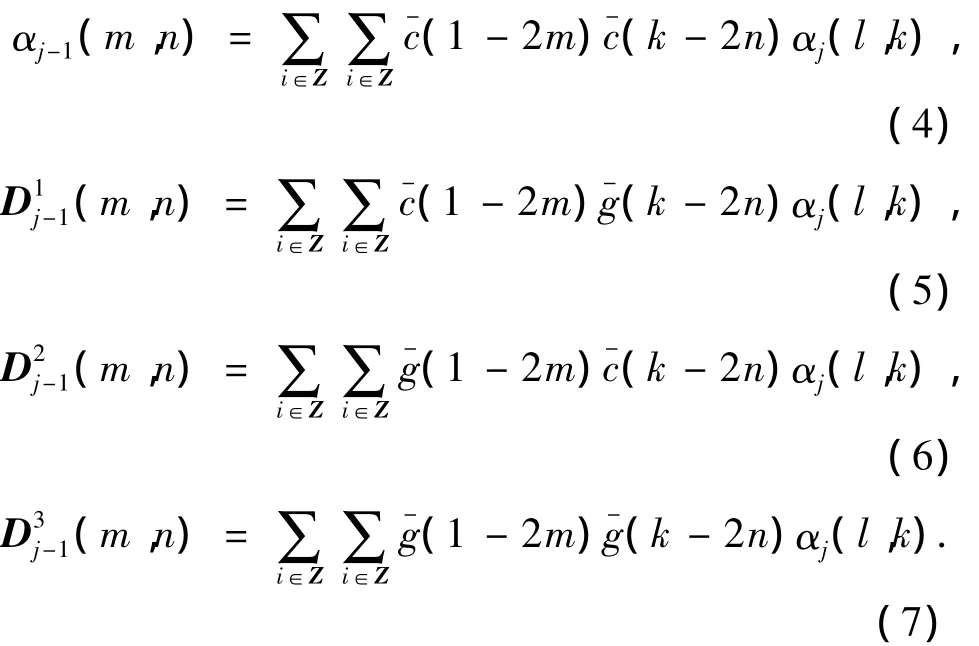
令Cr、Gc分别表示对 αj(l，k)的行与列作低通滤波运算，而 Cr、Gc分别表示对 αj(l，k)的行与列作高通滤波运算，图像f(x，y)二维Mallat算法分解的矩阵表示可以描述为

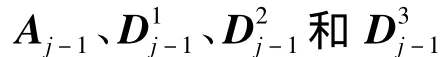
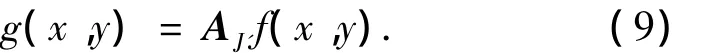
则相应的微细电火花线切割表面三维粗糙度s(x，y)为

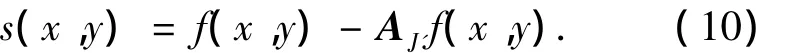
相应地，其二维Mallat重构算法的矩阵表示满足:

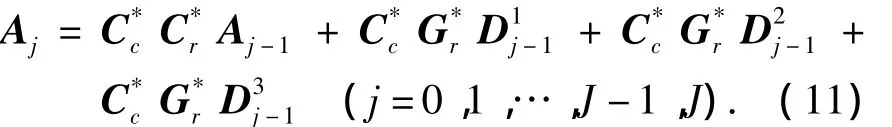
式中:C*、G*分别为C、G的共轭转置矩阵.

2.2 小波基的选取

小波滤波克服了传统滤波方法的缺陷，可以实现表面的多尺度分析，但小波分析的基函数具有不唯一性，同一工程表面用不同的小波基进行分析有时结果相差甚远［9］.如何选择小波基波，到目前为止还没有一个统一的理论标准.在实际应用中，一般是根据信号处理目的不同，经验性的选取一些小波.对于数字信号常用的正交小波有 Daubechies、coiflets和 symlets小波基［10］.

用小波变换分析微细电火花线切割加工表面时，首先对表面微观三维形貌在不同尺度上进行多分辨率分解，然后再重构所需要的特征信息.用不同的小波分解同一表面信息时会得到不同的结果，相应的重构出来的表面特征信息也不同.所以用小波重构的特征信号无法作为比较不同小波基对所分析表面信号的优劣依据，微细电火花线切割加工原始表面信号是确定的，如果用不同的小波基在相同的分解次数下重构原始表面信号，其重构效果就能在一定程度上反映出相应的小波基对所分析表面的精确性.

微细电火花线切割加工表面信号是以离散信号形式存在的，在实际应用中，信号的可分辨率是有限的.不可能计算在所有尺度2j(-∞ ＜j＜∞)上的小波变换，分辨率2J应取有限值.把变换限定在一个有限的最大尺度j=J和最小尺度j=0之间，20表示最高分辨率，2J表示最低分辨率.

试验中，扫描图像时轮廓上的采样点数为N=512个.在进行小波变换时，最大理论尺度:

即表面信号最多能分解9次.而当分解到第9次时，只剩下1个数据点，用1个点代替1个表面对处理表面信号已经没有意义了.故在选择最优小波基时只进行8次分解再重构表面信号.

采用3种小波对微细电火花线切割表面三维形貌进行8分解再重构原始信号，取重构形貌与原始形貌二范数来判定所选小波基的优劣.表1为对图1微细电火花线切割表面三维形貌的小波重构误差.

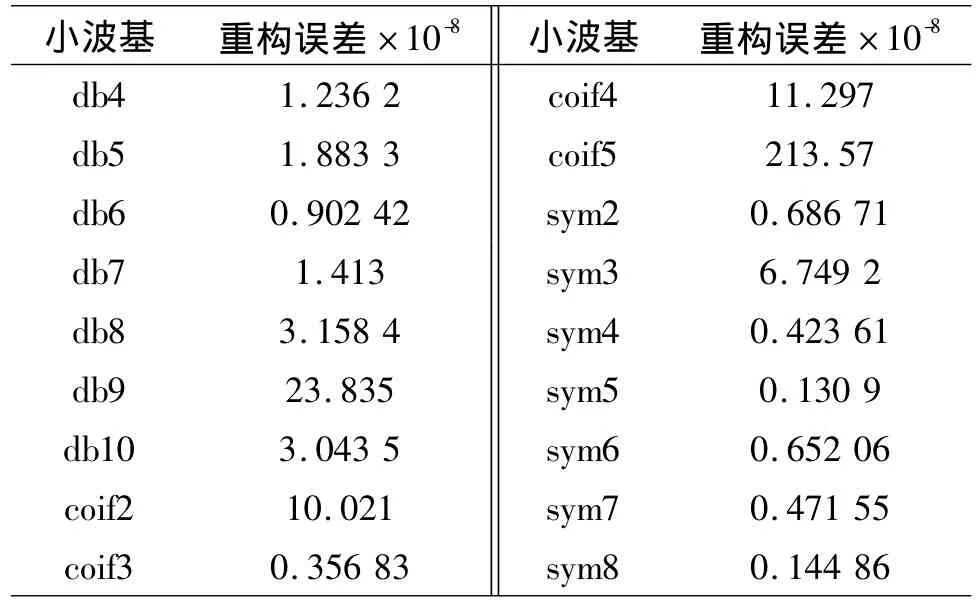
表1 不同小波基的重构误差Table 1 Reconstruction error of different wavelet bases

从表1中可以看出用sym5小波基对微细电火花线切割表面三维形貌分解再重构后得到的图像与原始图像相比，误差最小.故选择sym5小波基作为微细电火花线切割表面的滤波工具.

2.3 确定小波分解次数

微细电火花线切割加工表面主要是由表面粗糙度、表面波纹度和几何形状误差3个频率成分组成的表面.由于正交小波变化有很好的去相关性，可以通过多次分解把三者很好地区分开来.小波变换具有尺度间呈指数退化的性质，同时小波变换同傅里叶变换一样是能量守恒的.当分解表面信号的某单一成分(如粗糙度信号)时，随着分解层数的增加，其幅值逐次变大，反映在能量上就是呈指数增长.

用小波对微细电火花线切割加工表面进行分解，所得N阶分量的能量是指该分量系数的平方和.首先用sym5小波对微细电火花线切割加工表面进行8层分解，计算各层分解的高频部分能量的百分比.通过检验各层分解信号的能量变化，来区分不同的频率成分，如图2所示.

图2中对所获得的微细电火花线切割加工表面进行了8次分解.在无法确定分解次数的情况下，根据上述分析对前4层或前5层分解能量的百分比做指数函数拟合.从图中可以看出，前6次小波分解的高频部分能量都较好的符合指数函数分布，当分解到第7层时能量分布出现突变.对前6层分解的能量进行指数函数拟合，拟合函数如下:

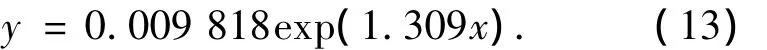
这完全符合小波分解的能量守恒规律，说明分解到前6层为止，都属于单一频率成分.小波分解时由高频到低频依次进行的，在微细电火花线切割表面的频率成分中，表面粗糙度属于高频信号，包括波纹度和几何形状误差的基准面属于低频信号.由此可见，对微细电火花线切割表面当分解到第7层时才能得到其小波基准面.

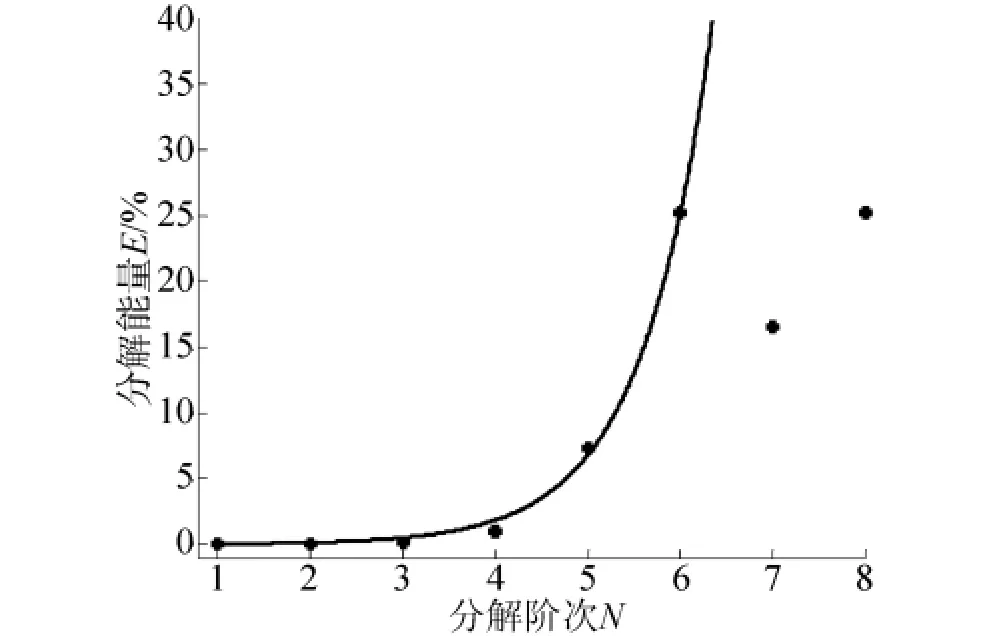
图2 小波分解阶次与分解能量的关系Fig.2 Relationship between wavelet decomposition level and decomposition energy

3 试验结果

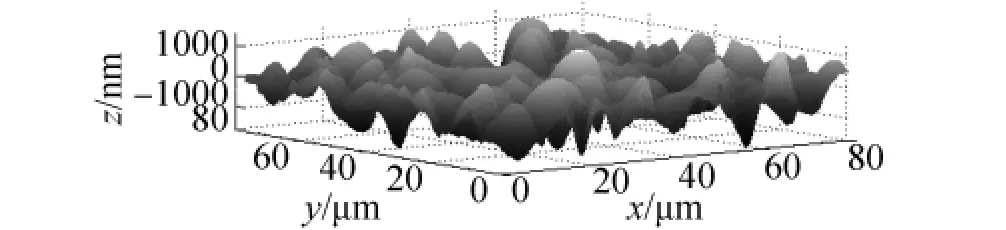
图3 微细电火花线切割加工实测三维表面Fig.3 The measured 3D surface of MWEDM

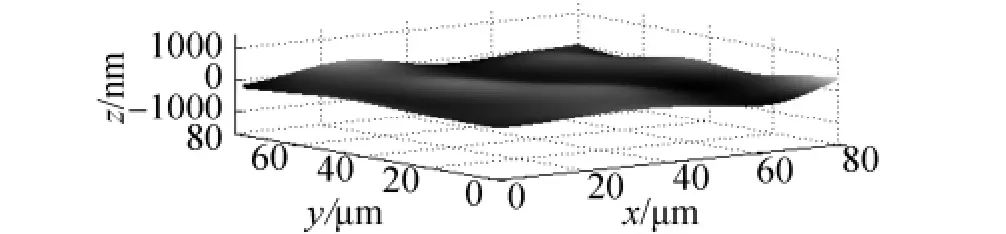
图4微细电火花线切割表面三维粗糙度的小波评定基准面Fig.4 The reference plane by wavelet for 3D roughness evaluation of MWEDM

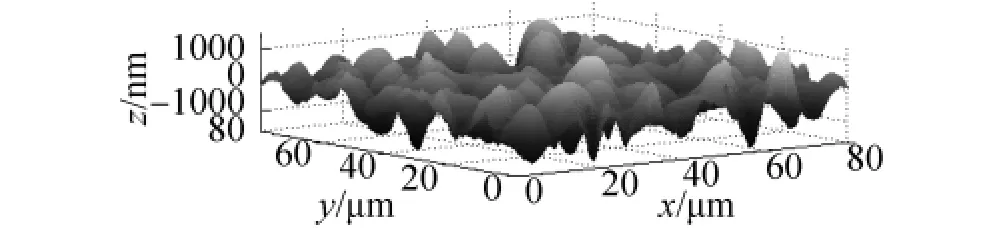
图5 微细电火花线切割表面三维粗糙度Fig.5 The 3D surface roughness of MWEDM

根据确定的最优小波基和小波基准面的分解次数对图3的微细电火花线切割表面进行小波处理，分离出小波基准面和表面三维粗糙度，结果见图4、5.

按照同样的方法，对外磨加工表面(图6)进行小波处理，分离基准面和三维粗糙度，结果见图7、图8所示.

由图4可知，微细电火花线切割加工表面的波纹度主要是由于加工时电板丝往复运动引起的振动和火花放电产生的热影响而产生的，故其波纹度不太规则.由图7可以看出，外磨表面的波纹谎要是由机床振动引起的，故其较为规则.

图6 外磨加工实测三维表面Fig.6 The measured 3D surface of cylindrical grinder

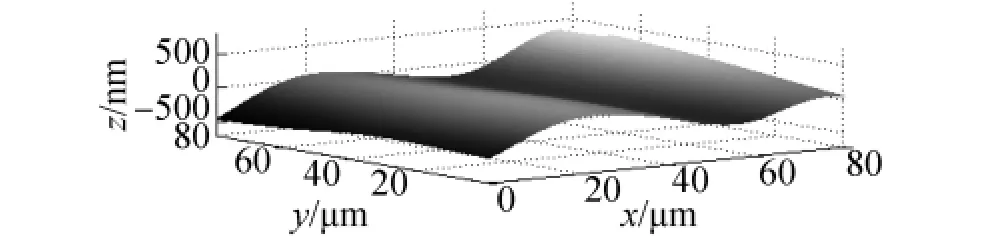
图7 外磨表面三维粗糙度的小波评定基准面Fig.7 The reference plane by wavelet for 3D roughness evaluation of cylindrical grinder

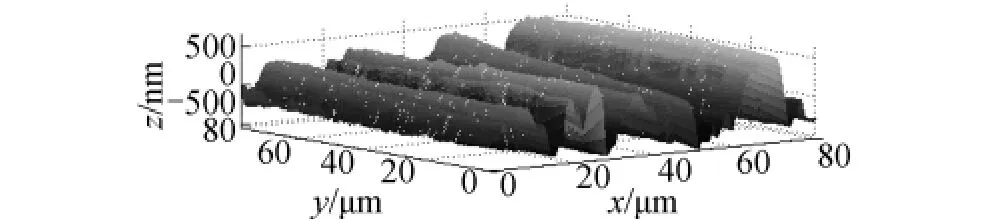
图8 外磨表面三维粗糙度Fig.8 The 3D surface roughness of cylindrical grinder

4 结论

采用小波分析方法分离了微细电火花线切割表面评定基准面，得到以下几点结论:

1)微细电火花线切割加工表面粗糙度、波纹度和几何形状误差之间既相互独立又高度相关，可以用小波变换的方法进行分离提取;

2)利用小波变换，以小波基重构的精度作为最优小波基的判断标准，根据小波分析的能量守恒原则，通过分析小波分解被测信号的能量变化能够准确确定小波分解次数.

3)表面粗糙度分析中最优小波基的选取和分解次数确定的方法可以推广到机械加工表面.

［1］PHAM D T，DIMOV S S.Micro-EDM—recent developments and research issues［J］.Journal of Materials Processing Technology，2004，49(2):50-57.

［2］DING Haijuan，GUO Libin，CUI Hai.Statistical characteristic and parameter characterization of 3D surface micro-topography on micro-EDM［C］.Proceedings of the IEEE International Conference on Automation and Logistics Shenyang.China 2009，113:1094-1098.

［3］陈庆虎，李柱.表面粗糙度评定的小波基准线［J］.计量学报，1998，19(4):254-257.

CHEN Qinghu，LI Zhu.Wavelet reference line for surface roughness evaluation［J］.Acta Metrological Sinica，1998，19(4):254-257.

［4］DI Shichun，CHU Xuyang，WEI Dongbo，et al.Analysis of kerf width in micro-WEDM ［J］.International Journal of Machine Tools and Manufacture，2009，8:788-792.

［5］陈庆虎，李柱.表面粗糙度提取的小波频谱法［J］.机械工程学报，1999，35(3):41-54.

CHEN Qinhu，LI Zhu.Wavelet reference line for surface roughness evaluation［J］.Chinese Journal of Mechanical Engineering，1999，35(3):41-54.

［6］李惠芬，蒋向前，李柱.三维表面功能评定技术发展综述［J］，华中科技大学学报，2002 36(2):8-11.

LI Huifen，JIANG Xiangqian，LI Zhu.Summary of development of 3D surface function evaluation technology［J］.Journal of Huazhong University of Science and Technology，2002 36(2):8-11.

［7］潘泉，张磊，孟晋丽，等.小波滤波方法及其应用［J］.电子与信息学报，2007，29(1):236-242.

PAN Quan，ZHANG Lei，MENG Jinli，et al.Walvelet filtering method and its application［J］.Journal of Electronics and Information Technology，2007，29(1):236-242.

［8］葛哲学，沙威.小波分析理论与MATLAB R2007实现［M］.北京:电子工业出版社，2007:108-112.

GE Zhexue，SHA Wei.Wavelet analysis theory and the realization of MATLAB R2007［M］.Publishing House of E-lectronics Industry，1999，2007:108-112

［9］CHEN Q H，YANG S N，LI Z.Surface roughness evaluation by using wavelets analysis［J］.Precision Engineering 1999，23(3):209-212.

［10］JIANG X Q，BLUNT L，STOUT K J.Application of the lifting wavelet to rough surfaces［J］.Precision Engineering，2001，25(2):83-89.