滑动轴承压力分布及动特性系数

史冬岩，张成，任龙龙，张亮，彭梁

(哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001)

滑动轴承在旋转机械中应用广泛，其工作时转子与轴承之间形成压力油膜.油膜压力作用在轴瓦的合金层上，循环交变的应力是导致轴瓦变形失效的主要原因.对油膜压力的计算和轴瓦合金层应力分布的研究是对滑动轴承进行设计和失效分析的重要理论依据.油膜不仅起着承受载荷、减轻摩擦、消除磨损等作用，从动力学观点看来，油膜的动特性对整个转子系统的动力特性有很大影响［1-3］.它也是转子—支承—基础这个系统中的一个环节［4］.

本论文以流体动压润滑滑动轴承为研究对象，以二维流动的雷诺方程作为研究的基础.对雷诺方程的求解是滑动轴承研究的关键问题之一，早期对雷诺方程的求解是基于解析解法，但解析解法无法获得较精确的解，随着计算机技术的发展.数值计算方法对雷诺方程求解己经成为一个主流趋势.有限差分法编程简单，求解方便，本文采用有限差分法求解雷诺方程［5-6］，在求解得出油膜压力分布的基础上研究轴瓦合金层的应力分布情况，并对滑动轴承的动态特性进行研究，求解出滑动轴承的动特性系数，为有限元分析中滑动轴承的简化提供帮助.

1 差分法求解压力分布

从层流运动的油膜中取一个微小的单元体作为研究对象，可以导出雷诺方程的一般形式［7］:

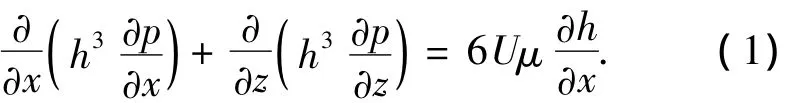
式中:x为周向坐标，z为轴向坐标，p为油膜压力，h为油膜厚度，U为轴颈速度，μ为油膜粘度.为了将方程写成最紧凑的形式，将式(1)无量纲化，可得雷诺方程的无量纲形式［8］为

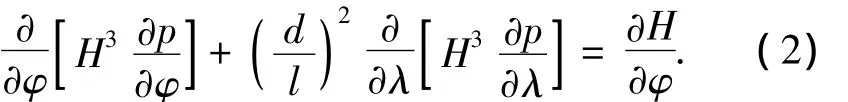
式中:φ为偏位角，l为轴承宽度，λ=2z/l，H=1+εcosφ，H为无量纲油膜厚度，ε为偏心率.P为无量纲油膜压力，由式(2)可以得出，无量纲油膜压力P的分布取决于偏心率ε和宽径比d/l.

本文选择采用有限差分法求解雷诺方程.将轴瓦的油膜区域划分为网格，如图1所示，用各个节点上的压力值构成各阶差商，近似取代节点上的压力值.所得的一组离散的压力数值，也就近似表达了油膜中的压力分布.先把整个油膜区域离散成长方形的网格，将网格节点按所在的列数和行数顺序编号，沿φ方向的列数用i编号，沿λ方向的列数用j编号，每个节点位置用(i，j)二维编号表示［9］.

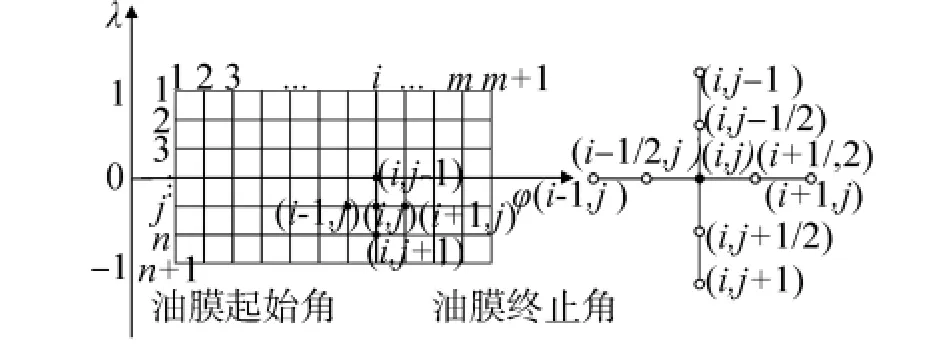
图1 网格划分及差商示意Fig.1 Schematic diagram of mesh generation and difference quotient

对节点(i，j)上的一阶导数，可用其相邻节点上的P值构成的中差商来表达，为了提高计算精度，采用半步长上的值构成的中差商表示一阶导数，对于(i，j)上的二阶导数，可先用相邻步长上的一阶导数的中差商表示，然后将式中的一阶导数用相邻节点值的中差商表示，则式(2)可表示为

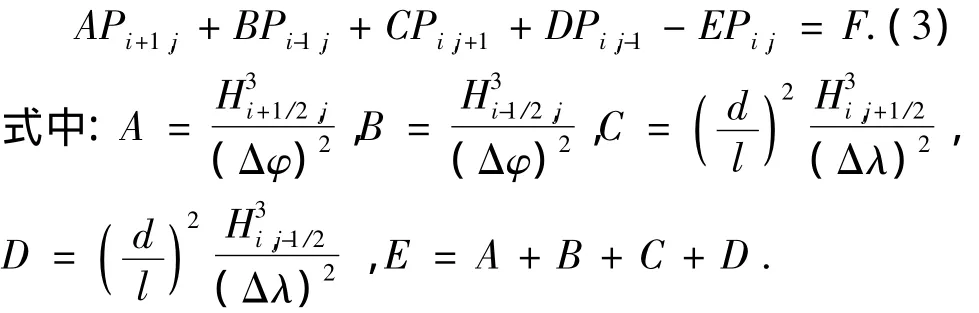
式(3)适用于全部内节点 i=2，3，…，m、j=2，3，…，n，共有 (m-1)(n-1)个方程，可构成一个方程组，根据给定边界条件可解出各内节点Pi，j值.

引入雷诺边界条件最常用的有效且简便的做法是:在网格区域每行上均由起始边向终止边方向逐点计算，如果算出某点压力为负，即取为零.此点位置即可作为该行上油膜自然破裂边的近似位置.该点以后各点压力均取为零，不按式(3)计算.每次迭代均如此处理，则破裂边近似位置会逐渐逼近应有的自然破裂边界，整个压力分布也就逼近计入雷诺边界条件的压力分布.

轴承参数取自文献［10］的一个计算示例，该示例中数据如表1所示.计入表1数据，取m=60，n=40得出一组无量纲油膜压力分布，其分布情况如图2所示.

表1 轴承参数Table 1 Bearing parameter

图2 油膜压力分布Fig.2 Pressure distribution of oil film

从压力分布图2中可以看出，360°包角有限宽径向轴承的无量纲油膜压力的分布为近似抛物面分布.无量纲油膜压力在某一段逐渐增大到最大压力值，之后急剧下降，在φ＞180°的某一区域，压力降为零，压力变为零的点就是油膜的自然破裂点.在油膜压力增大到最大的过程中，油膜压力变化平滑，在超过峰值后，油膜压力变化几乎突变为零，这与实际情况中楔形油膜的变化情况一致.

2 合金层应力应变分布求解

根据表1数据建立滑动轴承网格模型，共生成单元数129 840个、节点数105 652个，外层钢材料采用五面体单元进行离散，内层的合金层采用六面体单元进行离散.钢被层和合金层材料属性如表2所示.

表2 轴承材料参数Table 2 Bearing material parameter

网格模型导入到ANSYS中，在前面编程求得的油膜压力分布式大量的无规则的、离散的值，选择用APDL命令进行加载.油膜压力加载情况如图3所示.求解得出的合金层应力应变分布如图4～6所示.

图3 油膜压力加载Fig.3 Oil film pressure loading

图4 滑动轴承轴瓦应力分布Fig.4 Stress distribution of sliding bearing bush

图5 滑动轴承轴瓦剪应力分布Fig.5 Shear stress distribution of sliding bearing bush

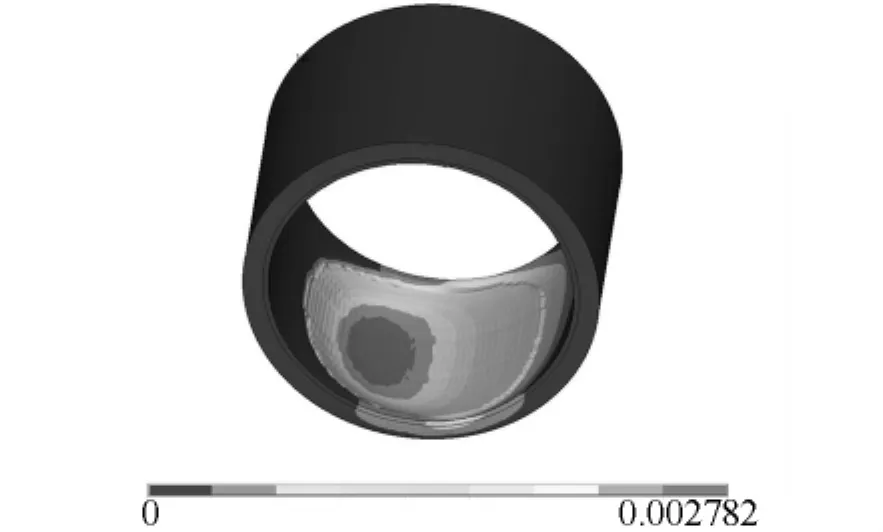
图6 滑动轴承轴瓦应变分布Fig.6 Strain distribution of sliding bearing bush

由图4合金层应力分布情况，可以看出，滑动轴承在承受油膜压力所产生的应力的分布与油膜压力的分布基本相同.在滑动轴承的宽度方向，应力从外截面到中截面逐渐增加，合金层轴向应力的峰值位于中截面油膜厚度最小处［11］，峰值为20.702 MPa.

由图5滑动轴承轴瓦剪应力分布情况，可以看出，剪应力存在的区域为压力峰值周围和压力梯度大的区域.同时，油膜压力最大值在滑动轴承的中截面处并具有最大压力梯度，剪应力的最大值在滑动轴承的中截面处合金层与钢被结合处，因为该处压力梯度最大，最大剪应力为8.375 MPa.在轴承表面，剪应力最大值在油膜压力分布峰值处，最大值为5.322 MPa.

由图6滑动轴承的应变分布情况，可以看出，滑动轴承在油膜压力作用下的径向变形与油膜压力分布十分相似，在一定区域内，变形随着油膜压力的增大而逐渐变大，当油膜压力达到最大值时，变形也达到最大.随着油膜压力急剧降低而使变形变小，应变随着油膜厚度的增大而逐渐减小.

3 滑动轴承动力特性系数计算

油膜不仅起着承受载荷、减轻摩擦、消除磨损等作用，从动力学观点看来，它也是转子—支承—基础这个系统中的一个环节.油膜通常起着非线性的弹簧和阻尼作用.由于这类问题大多只涉及到较小振幅或无限小的振幅，所以常可将油膜近似看成具有线性化了的弹簧常数和阻尼特性，通常即称这些线性化了的动力特性为油膜刚度和阻尼，下面介绍油膜刚度和阻尼系数［7］的求解.

3.1 等效力学模型

定义油膜刚度系数为单位位移所引起的油膜力增量，即

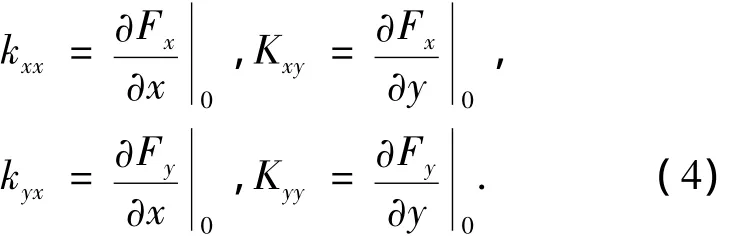
定义油膜阻尼系数为单位速度所引起的油膜力增量，即

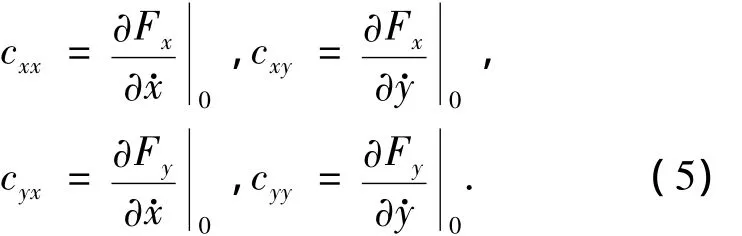
式中，各系数的第1个下标代表力的方向，第2个下标代表位移或速度的方向.油膜刚度系数和阻尼系数统称为油膜动力特性系数或动力系数.动态分析时滑动轴承的力学模型可表示成如图7所示情况［12］.

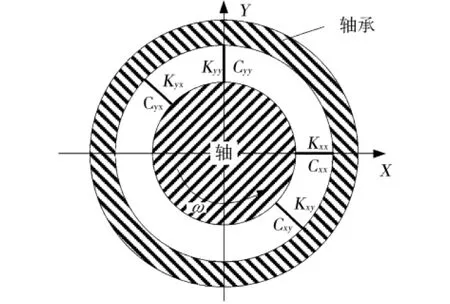
图7 滑动轴承等效力学模型Fig.7 Equivalent mechanical model of sliding bearing

3.2 扰动压力方程求解

径向滑动轴承的非定常运动雷诺方程为

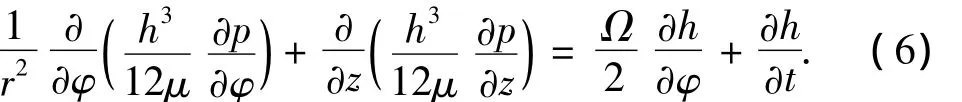
式中:h为油膜厚度，p为油膜压力，μ为润滑油膜动力粘度，φ为轴颈轴向位置，z为轴向位置，r为轴颈半径，Ω是轴颈角速度，t为时间.

设Δx为横向扰动、Δy为垂向扰动、h0为静平衡油膜厚度 ，将(6)式按 h=h0+ Δxsin φ -Δycos φ展开，并忽略高阶小量，可以获得各项扰动压力的微分方程为［13］

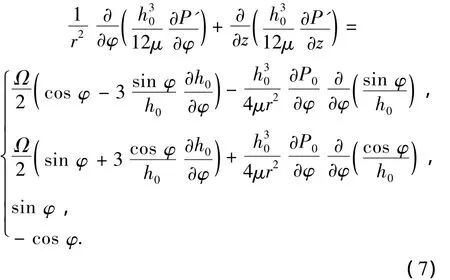
式中，P'分别表示Px、Py、P˙x、P˙y、P0为静平衡时的油膜压力.第1个方程为Δx对应项，第2个方程为Δy对应项，第3个方程为Δ˙x对应项，第4个方程为Δ˙y对应项.各扰动方程与无扰动下雷诺方程形式一样，只是右边项不同，故求解方法和求解无扰动下雷诺方程一样，在求解前需把扰动方程无量纲化.令

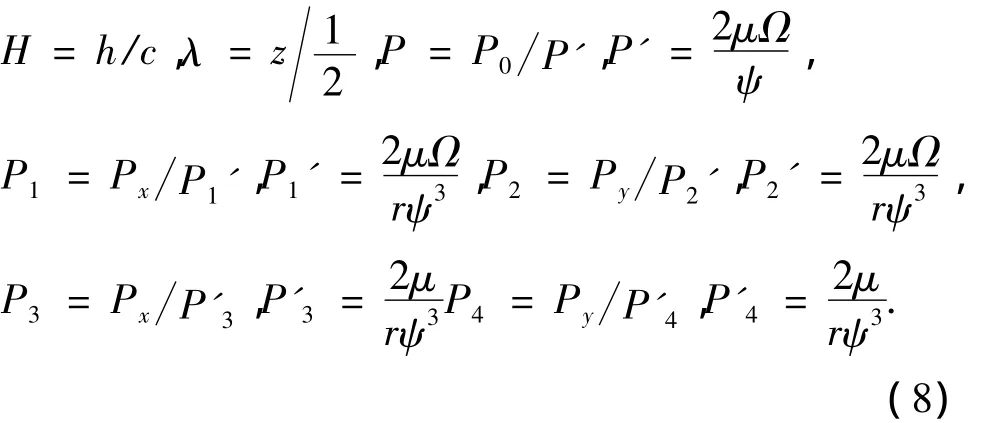
式中:ψ =c/r.

将式(8)中各无量纲因子带入式(7)即可得出扰动压力微分方程的无量纲形式如下:

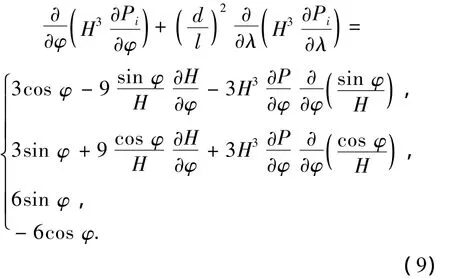
式中:Pi分别表示 P1、P2、P3、P4的无量纲形式.

式(9)表示的是无量纲扰动压力与静压力分布、油膜厚度、周向位置之间的关系.由式(9)中第3个、第4个方程可以看出动态速度引起的油膜压力增量P3、P4与静平衡位置时油膜压力分布情况和油膜厚度分布情况无关.

3.3 无量纲动特性系数的计算

求解扰动压力即解方程(9)，求解方法和求解无扰动下雷诺方程一样.对于这些扰动压力，边界条件是:在完整油膜区的全部边界上，这些扰动压力均为零.在计算时，先按求解出轴心静平衡位置相应的压力分布，以及由雷诺边界条件确定的破裂边位置，然后按方程(9)计算各扰动压力.当计算出各扰动压力 P1、P2、P3、P4后，经再次积分求出油膜力的各项增量，即无量纲刚度系数如式(10)所示，无量纲阻尼系数如式(11)所示:

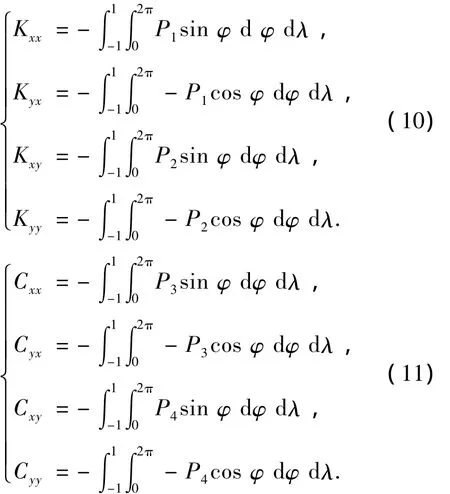
求解得出无量纲油膜动特性系数如表3所示.由表3可以看出，滑动轴承油膜无量纲刚度和阻尼系数随着偏心率的增大而增大，在偏心率小于0.5时，随偏心率的变化不大;当偏心率大于0.5后，随偏心率的增大而迅速增大;当偏心率超过0.8时，该趋势变的更加明显.另外可以看出，交叉阻尼系数近似相等.这一点也可以有力的证明前面所采用的算法是可行的，因为由滑动轴承动态特性的经典理论知道滑动轴承油膜交叉阻尼是相等的，在本文中由于采用数值计算方法，二者近似相等.

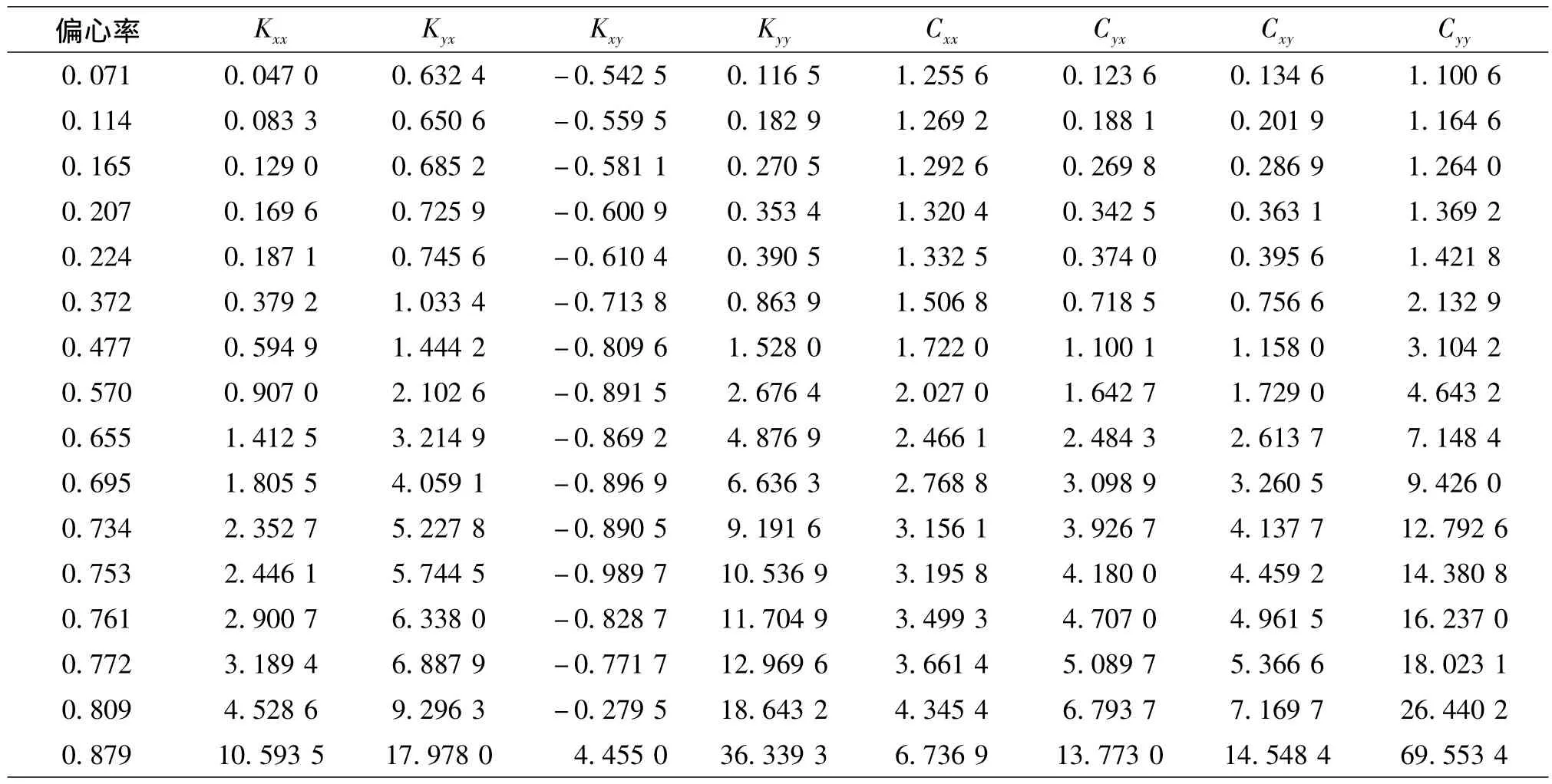
表3 无量纲油膜动特性系数(L/D=0.5)Table 3 Dynamic characteristics of oil film with dimensionless(L/D=0.5)

4 结论

本文对滑动轴承的油膜压力和轴瓦合金层应力分布进行了研究，在求解出油膜压力分布的基础上对滑动轴承的动态特性进行了研究，求解出滑动轴承的动特性系数，主要得出了以下结论:

1)由油膜压力分布图可得出滑动轴承的压力分布为近似抛物面分布.无量纲油膜压力在某一段逐渐增大到最大压力值，之后急剧下降，在φ＞180°的某一区域，压力降为零.

2)滑动轴承合金层在承受油膜压力所产生的应力分布与油膜压力的分布基本一致，应力峰值为20.702 MPa.剪应力存在的区域为压力峰值周围和压力梯度大的区域，最大剪应力为8.375 MPa.

3)滑动轴承油膜无量纲刚度系数和阻尼系数随着偏心率的增大而增大，交叉阻尼系数近似相等.

［1］姚熊亮，孙士丽，陈玉.高频动载轴承内油膜压力特性［J］.机械工程学报，2010，46(17):93-99.

YAO Xiongliang，SUN Shili，CHEN Yu.The pressure behavior of oil film in bearing subjected to high-frequency dynamic load［J］.Journal of Mechanical Engineering，2010，46(17):93-99.

［2］邓玫，孙军，符永红，等.计及轴受载变形的粗糙表面轴承热弹性流体动力润滑分析［J］.机械工程学报，2010，46(15):95-101.

DENG Mei，SUN Jun，FU Yonghong，et al.Thermoelastohydrodynamic lubrication analysis of bearing considering shaft deformation and surface roughness［J］.Journal of Mechanical Engineering，2010，46(15):95-101.

［3］姚熊亮，张成，孙士丽.考虑可压缩性及惯性力的油膜力研究［J］.中国舰船研究，2010，5(6)33-40.

YAO Xiongliang，ZHANG Cheng，SUN Shili.Analysis of oil film force considering compressibility and inertial force［J］.Chinese Journal of Ship Research，2010，5(6):33-40.

［4］全永昕.工程摩擦学［M］.杭州:浙江大学出版社，1994:222-250.

QUAN Yongxin.Engineering tribology［M］.Hangzhou:Zhejiang University Press，1994:222-250.

［5］王兆伍，杨家富，徐尚贤.流体润滑轴承静动态特性的有限分析法［J］.南京林业大学学报，1996，20(4):32-42.

WANG Zhaowu，YANG Jiafu，XU Shangxian.The finite analytic method on static and dynamic performance of journal bearings［J］.Journal of Nanjing Forestry University，1996，20(4):32-42.

［6］高创宽，齐秀梅.雷诺方程数值解中的几个问题［J］.太原重型机械学院学报，1993，18(6):30-41.

GAO Chuangkuan，QI Xiumei.Several problems in the numerial solution to Reynolds'equation［J］.Journal of Taiyuan University of Science and Technology，1993，18(6):30-41.

［7］张直明.滑动轴承的流体动力润滑理论［M］.北京:高等教育出版社，1986:1-5，34-46，65-72.

ZHANG Zhiming.Hydrodynamic lubrication theory of sliding bearing［M］.Beijing:Higher Education Press，1986:1-5，34-46，65-72.

［8］黄民毅.液体动压滑动轴承设计的数值计算［J］.四川工业学院学报，1998，17(3):37-41.

HUANG Minyi.Numerical calculation in the design of sliding bearings with liquid dynamic lubrication［J］.Sichuan U-niversity of Science and Technology，1998，17(3):37-41.

［9］王宁.基于MATLAB的滑动轴承压力分布的数值计算［D］.大连:大连理工大学，2006:1-3.

WANG Ning.Numerical Calculation to the pressure distribution of journal bearing based on the Matlab［D］.Dalian:Dalian University of Technology，2006:1-3.

［10］机械设计手册委员会.机械设计手册(第三卷)［M］.北京:机械工业出版社，2004:21-25.

Standard Handbook of Machine Design Committee.Standard handbook of machine design-Ⅲ［M］.Beijing:China Machine Press，2004:21-25.

［11］唐倩，方志勇，朱才朝，等.滑动轴承油膜压力及合金层应力分布［J］.中南大学学报，2008，39(4):776-779.

TANG Qian，FANG Zhiyong，ZHU Caichao，et al.Oil film pressure and stress distribution in alloy layer of journal bearing［J］.J Cent South Univ，2008，39(4):776-779.

［12］曹树谦，丁千，陈予恕，等.具有滑动轴承的稳态转子系统有限元建模分析［J］.汽轮机技术，1999，41(6):347-350.

CAO Shuqian，DING Qian，CHEN Yushu，et al.Analysis on modeling steady rotor system with sliding bearings by using FEM［J］.Turbine Technology，1999，41(6):347-350.

［13］钟一鄂.转子动力学［M］.北京:清华大学出版社，1987:41-50.

ZHONG Yi’e.Rotor dynamics［M］.Beijing:Tsinghua U-niversity Press，1987:41-50.

［14］SUN Jun，GUI Changlin.Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation［J］.Tribology International，2004，37:841-848.

［15］孙军，王震华，桂长林.计入曲轴受载变形的粗糙表面曲轴轴承弹性流体动力润滑分析［J］.机械工程学报，2009，45(1):135-140.

SUN Jun，WANG Zhenhua，GUI Changlin.Elastohydrodynamic lubrication analysis of crankshaft bearing considering crankshaft deformation under load and roughness surface［J］.Journal of Mechanical Engineering，2009，45(1):135-140.

［16］SUN Jun，GUI Changlin.Effect of lubrication status of bearing on crankshaft strength［J］.Journal of Tribology，Transactions of the ASME，2007，129:887-894.

［17］柳江林，孙军，桂长林，等.轴颈倾斜轴承的热流体动力润滑分析［J］.润滑与密封，2007(9):60-63，32.

LIU Jianglin，SUN Jun，GUI Changlin，et al.Thermohydrodynamic lubrication analyses of misaligned journal bearing［J］.Lubrication Engineering，2007(9):60-63，32.