静电场分析的比例边界有限元法

刘 俊， 林 皋＊， 王 复 明， 李 建 波

（1.大连理工大学 建设工程学部 水利工程学院，辽宁 大连 116024；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；3.郑州大学 水利与环境学院，河南 郑州 450002）

0 引 言

静电场求解主要有解析法、半解析法和数值解法三大类.解析法的优点是能够得到精确的解析式，直观地看出各物理量间的变化关系，但只适用于简单的几何边界、简单的物理参数.20世纪80年代初期，人们对半解析解进行了研究，其主要方法有级数法、多极点法、广义多极技术、多极理论方法和新型等效源法[1～4]等.这些方法在电磁计算方面取得了较好的效果和较广泛的应用，但该类方法有时也只适用一些几何形状比较规则的静电场问题.数值计算方法是随着计算机的问世应运而生的.该类方法中有有限差分法、有限元法、边界元法、矩量法、无网格法[5～9]等.其中有限差分法网格剖分容易，编制程序方便，但对不规则的复杂边界，网格剖分缺少灵活性.有限元法是分析静电场问题适应性最强、最通用的方法之一，因为该方法适合于含有复杂媒质（包括非线性媒质以及各向异性媒质等）问题的数值分析.但该方法在处理含有场值奇异点以及不同材料交接点等问题中遇到很大的挑战，通常的处理方法是在这些点周围增加节点，但这势必需要更多的前处理和计算工作时间，当然也有很多改进的有限元法，例如提高形函数阶段或者使用超级单元等.与此同时，边界元法也可以很好地解决该类问题.它降低了待求问题的维数，简化了数据的处理，直接求解无界边值问题精度较高.但该方法的缺点是有时找不到对应的基本解.无网格法只需节点，不需单元，适合处理复杂边界问题，计算精度高、收敛速度快.但针对某些问题，其基函数的选取及节点布置对计算精度的影响等问题还有待于进一步研究.从以上分析可以看出，各种解法有各自的优缺点，采用一种方法，有时得不到满意的结果，为此，近年来出现了将不同方法相结合的方法.例如，有限元－边界元法、有限元与无单元耦合法、多极理论－边界元耦合法、边界元法与无网格局部Petrov－Galerkin法的耦合法[4、10～12]等.

比例边界有限元法（scaled boundary finite element method，SBFEM）是20世纪90年代由Wolf和Song等[13]率先提出和发展起来的一种半解析的数值方法.该方法综合了有限元法和边界元法的优点，只需用有限元离散部分边界，从而实现了将问题降低一维的目的，而在没有离散的坐标方向利用解析方法求解.与传统有限元法比较，它显著降低了计算工作量.相对于边界元法，它不需要基本解，也不存在积分的奇异性问题，具有较高的计算精度，对于各向异性，以及物理性质沿某一方向发生特定变化的问题处理也比较方便.目前这种方法已被用于求解有限域、无限域的弹性静力问题、动力学问题、水库坝体与水体的相互作用问题、断裂力学、绕流场和势流场问题、液体晃荡问题、波浪与结构相互作用问题、声学问题、渗流问题[14]等.本文首次将该方法应用于静电场问题的求解.从静电场控制方程——拉普拉斯方程出发，结合加权余量法推导静电场分析的比例边界有限元方程，引入特征值问题对该方程进行求解并得出电位和电场的计算公式；以二维静电场为例通过数值算例验证比例边界有限元法求解静电场问题的高效性和精确性.

1 静电场的比例边界有限元方程推导

描述静电场（域内无电荷）特性的控制方程为拉普拉斯方程（ 为电位）：

存在两类边界条件：一类是在边界上给定电位值，一类是给定电场值，即

对于以上静电场控制方程和边界条件问题的比例边界有限元方程推导，首先需建立笛卡儿坐标系统和比例边界有限元坐标系统转换关系.考察图1所示的有限区域和无限区域，在域内选择一点O作为比例边界有限元的相似中心（要求整个计算域必须在相似中心可视化的范围之内，也就是边界各点与相似中心均可用直线进行连接），建立以点O为中心的ξ和s坐标体系.其中有限区域0＝ξ0≤ξ≤ξ1＝1、无限区域1＝ξ0≤ξ≤ξ1＝∞.计算区域内的点在比例坐标系统下可以表示为

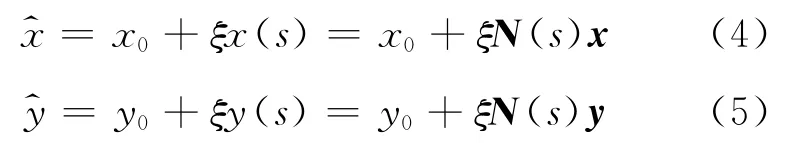
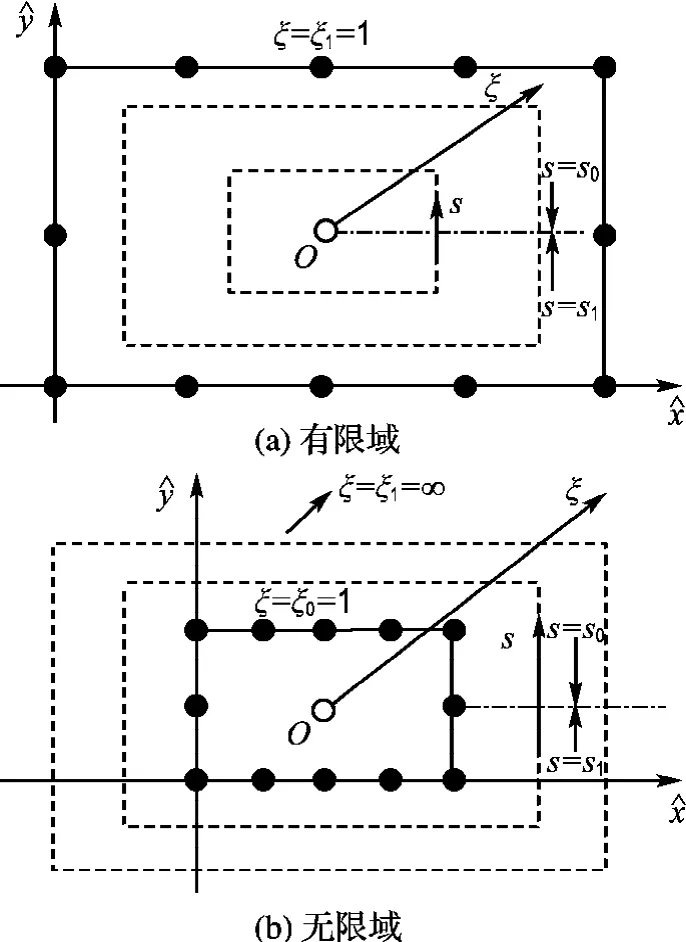
图1 比例边界有限元法计算示意图Fig.1 Sketch for scaled boundary finite elementmethod

两坐标系统可通过雅克比矩阵联系起来：

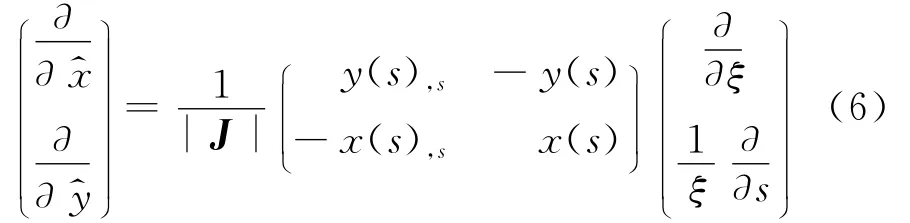
其中

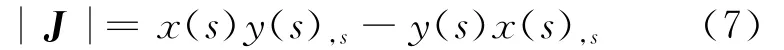
在比例坐标下梯度的算子可以表示为

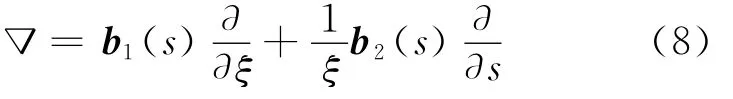
其中

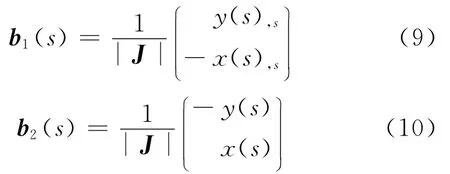
对方程（1）、（2）、（3）利用加权余量法和格林第一公式可得（w为权函数）

根据等参变换概念，电位函数可采用相同的插值函数N（s）进行离散：

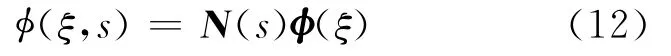
方程（11）中权函数w也用同样的形函数表达：

将式（12）、（13）代入式（11）可得

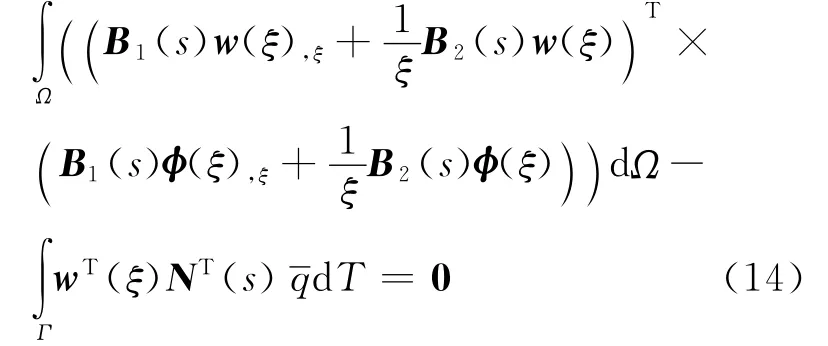
其中

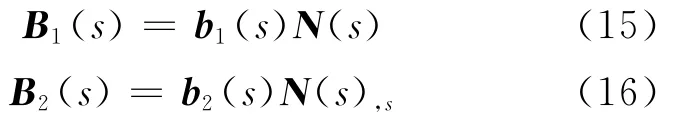
比例坐标下的空间微元面积

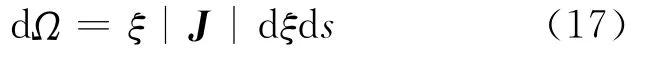
比例坐标下的边界微元线长度

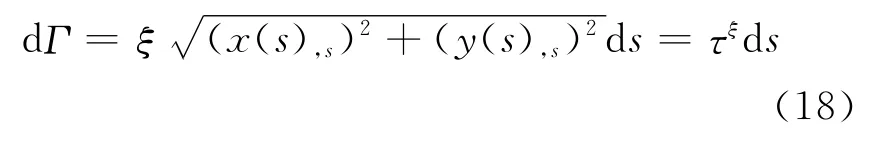
其中τξ为关于ξ的函数.

对式（14）中含w（ξ，s），ξ项做分部积分，并将式（17）、（18）代入可得

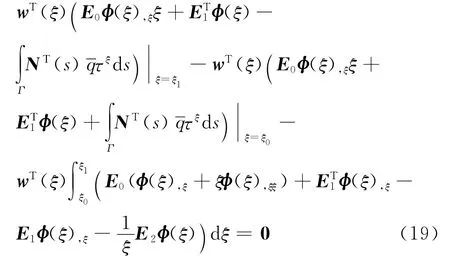
方程（19）的系数为

考虑方程（19）中w（ξ）任意性可得

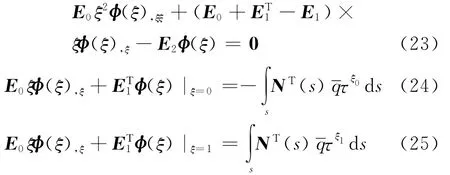
方程（23）为比例边界有限元的基本方程.方程（24）、（25）为需要满足的计算域内、外边界条件.对于有限区域（0＝ξ0≤ξ≤ξ1＝1），内边界条件式（24）为相似中心一点，外边界条件式（25）为离散边界；对于无限区域（1＝ξ0≤ξ≤ξ1＝∞），内边界条件式（24）为离散边界，外边界条件式（25）为无穷远处外边界条件.

2 比例边界有限元方程求解

式（23）为二阶Euler－Cauchy齐次方程，为了便于降阶求解，从式（24）、（25）特性看出，引入Q（ξ）作为 （ξ）的对偶变量：

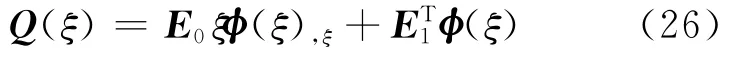
由此可得具有两倍未知数的变量：

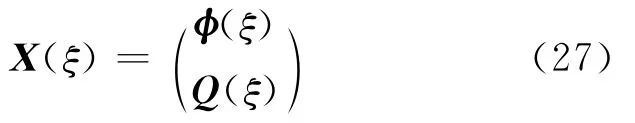
可将式（23）化为状态方程：

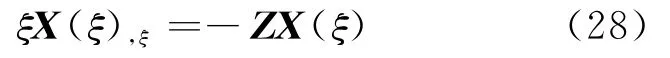
其中

由于Z阵为Hamilton阵，可以通过求解Z的特征值问题来得到式（30）的解（式（31）特征值中成对出现，互为负号）：

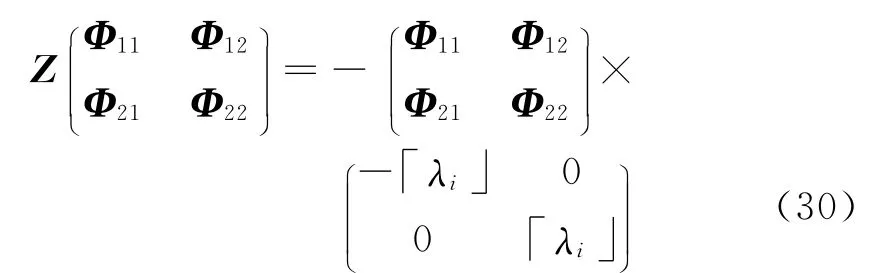
由此方程（30）的解为

将方程（27）代入方程（31）可得

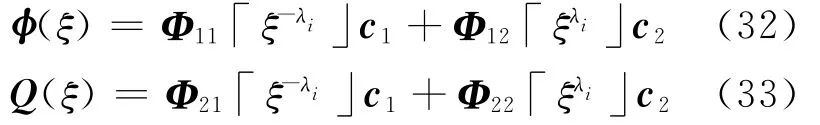
式中：c1、c2为积分常数.对于有限域问题，ξ＝0处的 取有限值，故c2＝0；对于无限域问题，ξ＝∞处的 取有限值，故c1＝0.有限域的积分常数c1和无限域的积分常数c2均可由边界条件确定.积分常数确定后，可由式（32）、（12）确定域内任意点的电位和由E＝－确定域内任意点电场强度.

3 算例计算分析

为了验证该方法数值模拟精度和高效性，本文首先选择了一个具有解析解和其他数值解的经典算例以便于对比.

算例1 一长直金属槽，侧壁与底面的电位为0，而顶面盖电位 （x，b）＝U0sin（πx/a），需求出域内的电位和电场.比例边界有限元计算示意图如图2所示，在仿真中，取a＝3.0 m，b＝1.0 m，U0＝1.0 V，相似中心放在域中心.

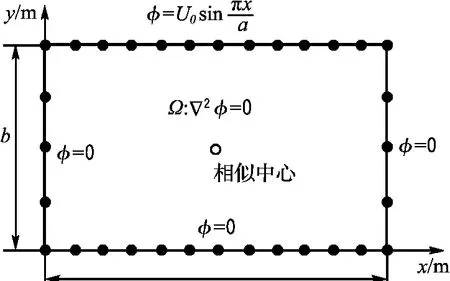
图2 比例边界有限元法算例1计算示意图Fig.2 Sketch for the first example using scaled boundary finite element method

表1为本文方法与文献[9]列出的有限差分法（FDM）、径向基无网格法（RBF）计算电位最大误差、相对均方根误差对比（电位单位为V）.相对均方根误差计算公式 （i＿exact为解析解，i＿calc为数值解）为

表1数据表明，比例边界有限元法精度非常高.在电场强度（单位为V/m）分析中，由于文献[9]没有给出相似节点分布下的计算结果，本文单独给出了本方法计算电场强度的相对均方根误差.边界为32节点的Ex相对均方根误差为1.8720%；边界为64节点的Ex相对均方根误差为0.5217%.边界为32节点的Ey相对均方根误差为2.0310%；边界为64节点的Ey相对均方根误差为0.7617%.同样可以看出本方法精度也比较高.电位解析解、SBFEM数值解（边界64节点）电位等值线分布如图3所示.从图中可以看出：比例边界有限元法和解析解非常吻合.与此同时，由于文献[9]没给出其他两种计算方法的计算耗时，为此，本文采用Intel Core Q8200（2.33 GHz）计算机对本算例的SBFEM 64节点模型进行计算时间测试，其消耗的时间不到1 s，由此看出计算效率比较高，而且比例边界有限元法前期准备（即单元划分）也少，主要的计算时间在特征值问题求解上.

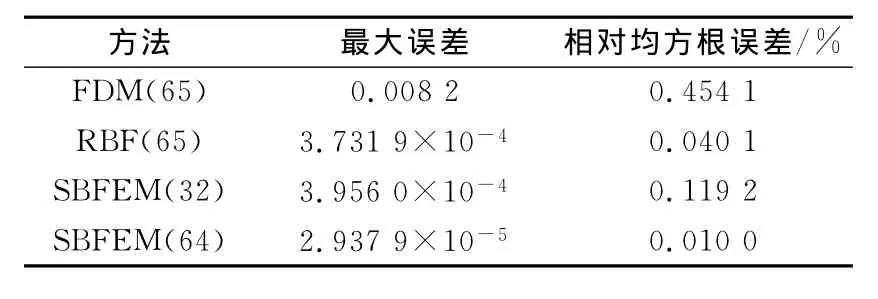
表1 不同方法的电位计算最大误差和相对均方根误差对比Tab.1 Maximum and mean square error′s comparison between different methods for potential calculation

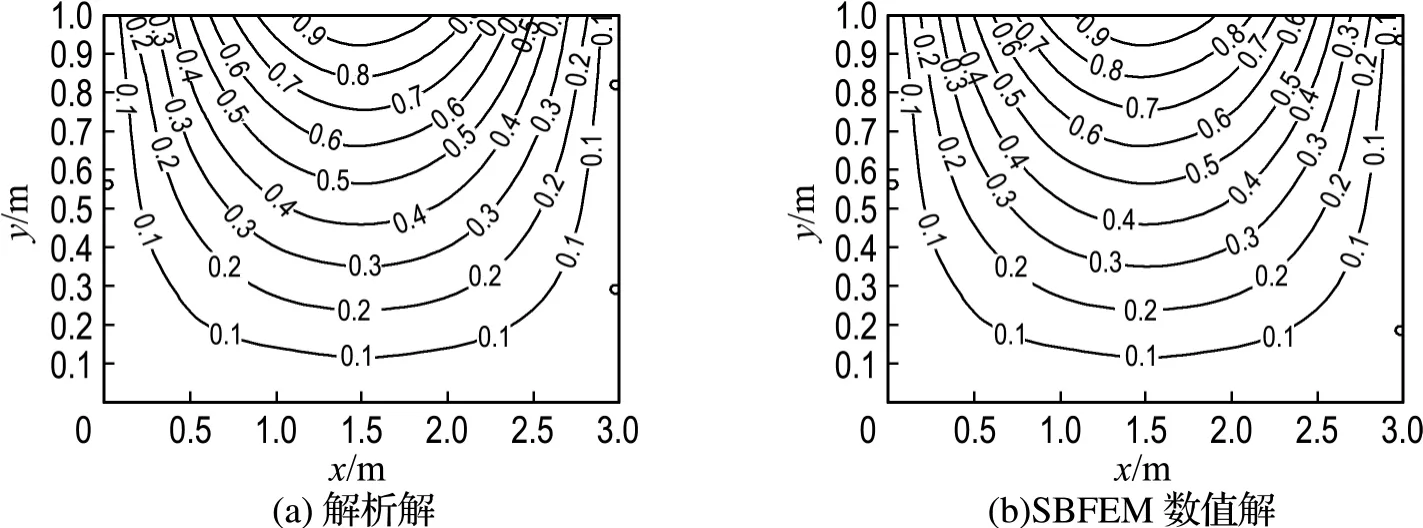
图3 算例1解析解和SBFEM数值解电位等值线Fig.3 Potential isolines of analytical and SBFEM solutions（Example 1）

比例边界有限元法对处理复杂边界条件问题计算精度也很高，为此本文选择如下算例.

算例2 有一二维静电场边值问题，边界由一段x＝a＝1.0 m的直线和x＝y2的抛物线围成，其定解问题及比例边界有限元示意图如图4所示.网格划分时，为了尽可能准确地描述抛物线边界形状，需要采用较多边界节点进行离散，为此选取在抛物线段上以x＝0.05 m为间距，在直线段上以y＝0.05 m为间距，得到80个边界节点.表2为本文方法与文献[15]列出的半解析方法——多极理论、边界元法计算所得电位、电场强度对比结果.可以看出比例边界有限元法计算复杂边界也具有很高的精度.

算例3 本算例为求一无限域问题.一无限长、半径R＝1.0 m圆筒被沿轴线切成两半，上一半电位为U0＝1 V，下一半接地（电位为0），如图5（a）所示.由于该问题是关于y轴对称问题，选取右半部分进行模拟.模拟中采用一有限子域和一无限子域，它们的相似中心放在同一点，离散边界选取33个节点，如图5（b）所示.筒内和筒外电位解析解和SBFEM数值解等值线分布如图6所示.从图中可以看出：比例边界有限元法数值解和解析解也非常吻合.

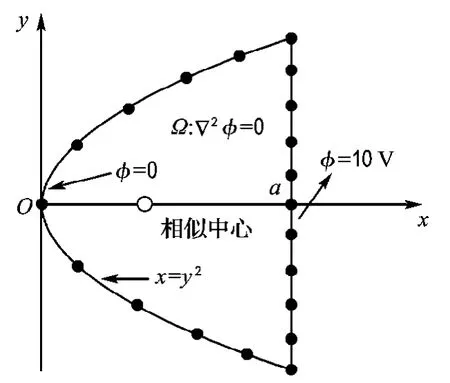
图4 比例边界有限元法算例2计算示意图Fig.4 Sketch for the second example using scaled boundary finite element method

表2 不同方法的电位计算结果比较Tab.2 Potential calculation result comparison between different methods

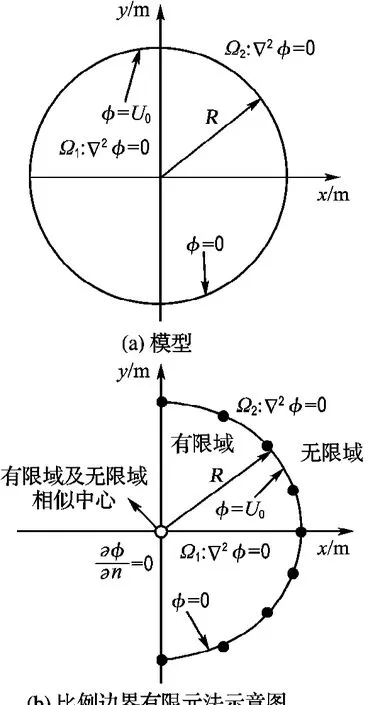
图5 模型和比例边界有限元法计算示意图Fig.5 Model and sketch for scaled boundary finite element method

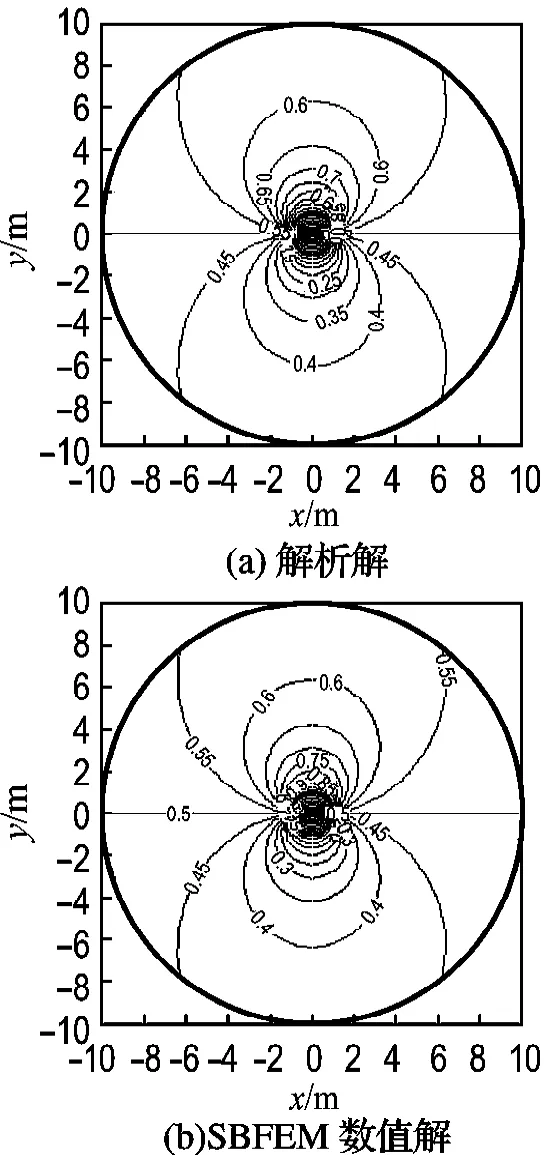
图6 算例3解析解和SBFEM数值解电位等值线Fig.6 Potential isolines of analytical and SBFEM solutions（Example 3）

4 结 论

本文提出了静电场分析的比例边界有限元法，推导了相应的控制方程，并利用特征值问题进行了求解.由该方法数值算例的结果与解析解、半解析解以及其他数值方法结果的对比发现该方法具有很高的精度和计算效率.

[1]李 敬.级数法求解轴对称的静电场[J].云南师范大学学报，1997，17（3）：43－45

[2]马西奎.最小二乘边界配点法在电磁场边值问题数值分析中的应用[J].微波学报，1994，37（2）：17－22

[3]BALLIST C H.The multiple multipole method in electro－and magnetostatic problems [J]. IEEE Transactions on Magnetics，1983，19（6）：2367－2370

[4]盛剑霓.电磁场与波分析中半解析法的理论方法与应用[M].北京：科学出版社，2006：1－35

[5]SONG B，FU J.Modified indirect boundary element technique and its application to electromagnetic potential problems [J]. IEE Proceeding H：Microwaves， Antennas and Propagation， 1992，139（3）：292－296

[6]金建铭.电磁场有限元方法[M].西安：西安电子科技大学出版社，1998：51－70

[7]BAMJI S S， BULINSKI A T. Electric field

calculations with the boundary element method [J].

IEEE Transactions on Electrical Insulation，1993，

28（3）：420－424

[8]樊德森.静电场边值问题的矩量法解[J].计算物理，

1989，6（1）：1－8

[9]张淮清.电磁场计算中的径向基函数无网格法研究[D].重庆：重庆大学，2008：25－36

[10]王江忠，赵 良，刘之方.二维开域静电场有限元与边界元迭代解法的研究[J].华北电力大学学报，2002，29（增刊）：36－40

[11]王志华.有限元与无单元耦合法在电磁场数值计算中的应用研究[D].石家庄：河北工业大学，2006：1－25

[12]李茂军.基于边界元法与无网格局部Petrov－Galerkin法的耦合法和区域分解法[D].重庆：重庆大学，2009：1－36

[13]WOLF J P，SONG C M.Consistent infinitesimal finite element cell method：three－dimensional vector wave equation [J].International Journal for Numerical Methods in Engineering，1996，39（13）：2189－2208

[14]LIU J，LIN G，WANG F M，etal.The scaled boundary finite element method applied to electromagnetic field problems [C] // IOP Conference Series：Materials Science and Engineering，Syndey，WCCM/APCOM 2010.London：IOP，2010

[15]郑勤红.计算复杂场域静电场问题的多极理论[J].电子科技大学学报，1997，26（6）：599－604