高强高性能细粒混凝土断裂特性研究

尹 世 平， 徐 世 烺

（1.大连理工大学 土木工程学院，辽宁 大连 116024；2.中国矿业大学 力学与建筑工程学院，江苏 徐州 221116；3.浙江大学 建筑工程学院，浙江 杭州 310058）

0 引 言

近十年来，采用纤维编织网增强水泥基材料得到了广泛的关注[1～4].纤维编织网增强混凝土（textile reinforced concrete，TRC）是一种结合了短切纤维增强混凝土和普通钢筋混凝土二者优点的复合材料.由于所采用的纤维材料（如耐碱玻璃纤维、碳纤维、芳族聚酰胺纤维等）具有耐腐蚀性，不再需要防止化学侵蚀的混凝土保护层，结构单元的厚度主要依赖于纤维编织网必需的锚固厚度[2].因此，这种新材料特别适用于薄壁轻质的结构，且能用于厚度仅有10～20 mm的构件，这是钢筋混凝土材料所不能做到的[3]；其也可用于结构的修补增强[3、4].

TRC构件应力应变状态的计算是与细粒混凝土的基本力学和断裂力学性能相关的[5、6]，而用于普通混凝土的断裂参数可能不再适用于细粒混凝土.由于TRC结构的特殊性，小尺寸的试件更适于获得代表薄壁结构单元结构行为的力学参数[6].文献[5、7]采用解析的方法获得了骨料最大粒径为0.6 mm的细粒混凝土的张拉应力与裂缝宽度的多线性软化本构方程，采用此方程得到的计算结果与有限元方法得到的结果吻合较好.但文献[7]只给出了失稳断裂韧度的计算方法，且是由σ－ω曲线下面积获得断裂能，其计算过程较复杂.为此，本文基于徐世烺等[8]建议的方法获得细粒混凝土的双K断裂参数，通过容易得到的荷载－位移曲线下面积来确定细粒混凝土的断裂能[9～12]，并研究不同的试件尺寸对双K断裂参数及断裂能的影响.

1 试验材料和方法

1.1 细粒混凝土

为保证混凝土能顺利渗透纤维编织网，要求其骨料最大粒径一般小于4 mm；为提高混凝土的强度，特别是早期强度，采用了PII52.5R硅酸盐水泥和硅灰；为提高混凝土的工作性能，掺加了I级粉煤灰.高性能细粒混凝土还具有高流动性、不离析的自密实能力，从而可与纤维束形成良好的黏结，避免孔穴，减少施工的难度.表1给出了高性能细粒混凝土的配合比[13].

表1 细粒混凝土的配比组成Tab.1 The composition of fine grained concrete

1.2 试件制备

本文分别对3种尺寸的细粒混凝土试件进行了研究，试验用A、B、C三种试件类型具体参数见后文.采用钢模成型试件，其抗压强度和弹性模量分别采用同批浇注的70.7 mm×70.7 mm×70.7 mm的立方体及40 mm×40 mm×160 mm的棱柱体测定.所有试件表面覆盖薄膜在室温下放置24 h后拆模，然后送入标准养护室（温度（20±3）℃，湿度不小于90%）中养护27 d后，取出对试件进行预切口，缝高比都为0.4.不同于常规的砂浆，细粒混凝土中掺加了硅灰和粉煤灰等活性矿物，这会使其后期强度有所增加.为了降低其强度增加对结果的影响，试验时试件龄期为56 d，材料的强度基本稳定，测定其立方体抗压强度为79.1 MPa，棱柱体抗压强度为73.2 MPa，弹性模量为30 GPa.

1.3 加载方式及测试内容

试验在30 t万能试验机上进行，如图1所示布置.加载采用等位移控制，尺寸为100 mm×100 mm×400 mm试件采用的加载速率为0.05 mm/min，其余试件采用的加载速率为0.02 mm/min.在试验中，由0.7 t荷载传感器（精度为最大量程的0.1%）测定荷载值，分别由两个夹式引伸仪（最大量程为4 mm，精度为0.001 mm）测得试件的挠度δ和裂缝口张开位移.采用文献[8]建议的电阻应变片法测定起裂荷载和观测裂缝的扩展.

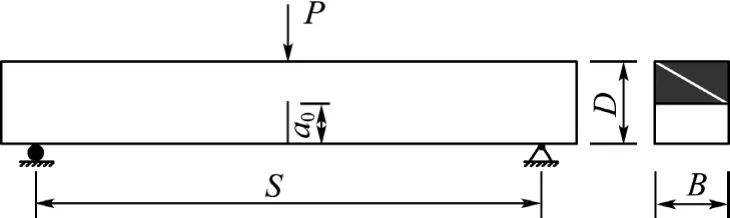
图1 三点弯曲梁试件形式Fig.1 Configuration of a specimens of three－point bending beam

采集系统用德国进口的动态采集系统IMC（integrated measurement ＆control），以准确地捕捉开裂荷载和失稳荷载，所有测量设备通过数据采集系统连接在电脑上，自动记录数据.

2 双K断裂参数的确定

本文采用由Xu等[14]提出的用于混凝土裂缝发展全过程稳定分析的双K断裂理论计算细粒混凝土的断裂参数.对于三点弯曲梁试件，通过试验获得的起裂荷载和失稳荷载及P－CMOD曲线，可得细粒混凝土的双K断裂参数，本文的计算结果考虑了试件自重的影响.

（1）临界有效裂缝长度ac的确定

将临界裂缝张开口位移CMODc和最大荷载Pmax代入下式计算[14]：

式中：H0为刀口的厚度；a0为预制缝长；B为梁的厚度；D为梁的深度.

（2）起裂断裂韧度KiniIc的确定

将a0和获得的起裂荷载Pini代入式（2）便可以确定起裂断裂韧度.对于图1所示加载形式的三点弯曲梁，其公式如下：

式中：G为在跨度S内试件的自重；缝高比α＝a0/D；F1（α）为形状因子，对于S/D＝4的三点弯曲梁，F1（α）的表达式为

（3）失稳断裂韧度KunIc的确定

用临界有效裂缝长度ac和破坏荷载Pmax代替式（2）中的初始裂缝长度a0和起裂荷载Pini；同时用失稳前缝高比αc＝ac/D代替式（3）中的α，即可获得KunIc.

图2给出了试验测得的不同尺寸试件的P－CMOD曲线，由图可见，细粒混凝土有与普通混凝土相似的裂缝发展过程，达到失稳破坏前也要经历一个裂缝稳定发展的过程，这一点也可以由表2中给出的Pini和Pmax的差值来说明.对于起裂断裂韧度的确定，试件起裂荷载的测定是关键.本文根据裂缝尖端两侧的荷载与拉应变关系来确定.图3给出了某一试件裂缝尖端一侧的荷载－应变曲线，在细粒混凝土达到其开裂强度前，是微观裂缝发展阶段，可认为试件处于线弹性阶段，随着荷载的增加，应变也成比例增加；一旦达到其开裂强度，细粒混凝土开裂，初始裂缝尖端两侧附近点的应变由于应力释放开始回缩，荷载－应变曲线上反映出荷载继续增加，而拉应变开始减小，此时所对应的荷载可认为是起裂荷载，如图3所示.由于试件两面可能不同时开裂及受应变片布设误差的影响，测得的数据难免有偏差，为此本文取试件两面起裂荷载的平均值作为该试件的起裂荷载，计算结果见表2.

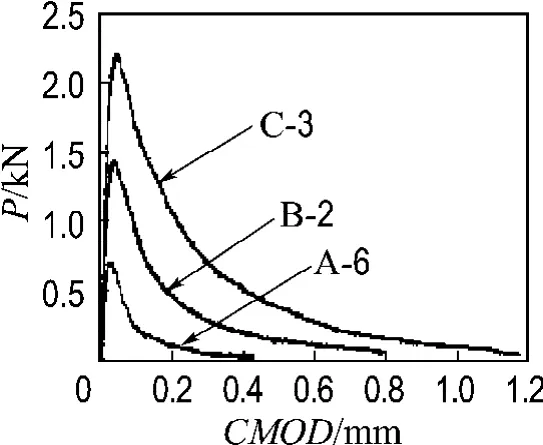
图2 不同尺寸试件的P－CMOD曲线Fig.2 P－CMOD curves of different sizes of specimens

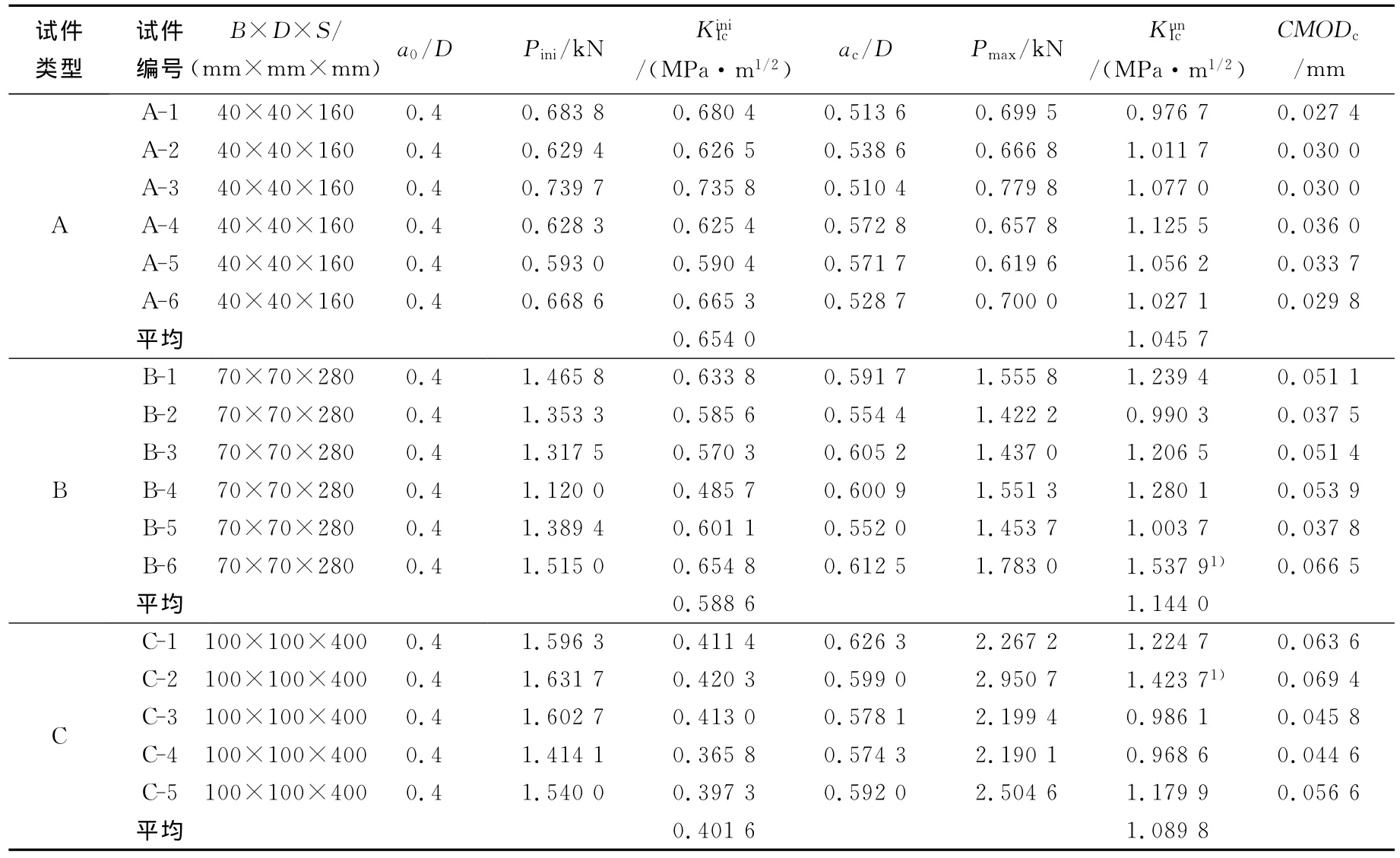
表2 试件的基本参数和测试结果Tab.2 The main parameters and calculated results of specimens

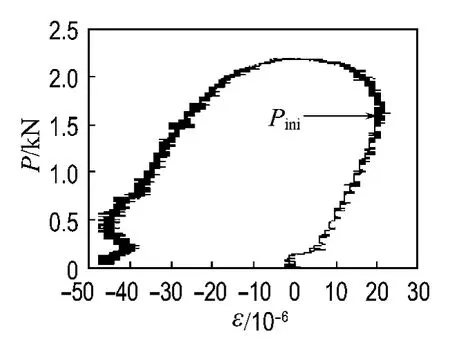
图3 起裂荷载的确定Fig.3 Determination of the initial cracking load

参考强度测试时均值的计算方法是将与其相差15%的个别值剔除，而本文在计算平均值时，考虑到混凝土断裂参数的离散性可能会更大一些，因此，在断裂韧度的均值计算时，将与均值相差20%的个别值剔除，在计算均值时未计入其影响.

由表2的计算结果可知，随着试件尺寸的变大，细粒混凝土的起裂断裂韧度有变小趋势，而失稳断裂韧度基本保持不变，这与文献[8]研究结论相同，但不同于普通混凝土的研究结果.对于普通混凝土，大量的研究成果表明[14、15]：混凝土的起裂断裂韧度KiniIc也认为是一个材料常数，没有明显的尺寸效应.细粒混凝土的起裂断裂韧度之所以有这样的变化趋势，可由其计算参数的取值来分析原因.由于采用人工切口的方式，不可避免地会对初始裂缝长a0产生影响，从而导致α发生变化，试件尺寸越小，这种误差产生的影响也越大.另外一点是起裂荷载的测量，应变片粘贴的位置、角度及所用底胶的量都会对测量值产生影响，试件尺寸越小，这种影响也越明显；而且，由于混凝土裂缝扩展的随机性，由不同试件获得的起裂荷载也有一定差别，小尺寸试件的离散性要更高一些，这由表2的结果可以证实.而失稳韧度的计算则可避免这些影响，因为根据裂缝口张开位移的实测值，由几何关系可获得ac的实际值，而由高精度荷载传感器可获得准确的Pmax.这一点也可由未切口试件的弯曲强度值得到证实，单独试验获得的A、B和C系列尺寸试件的三点弯曲强度值分别为5.72、6.00、5.43 MPa，它们与中间值的最大误差仅为5.1%，几乎没有尺寸效应.由于本文试件尺寸种类有限，还需要进一步的试验来研究这个问题.

3 断裂能的确定

研究水泥基材料的非线性断裂特征，断裂能是一个重要参数.三点弯曲法因其简便易行，对试验机没有太高要求，适合于一般条件的实验室，已经成为获得混凝土断裂能使用最多的方法.

为了确保荷载－挠度曲线的准确性，以试件的中心轴作为测量跨中挠度的基准点，可以消除其他部位变形的影响[12].图4为采用三点弯曲法确定混凝土断裂能的示意图.图中实线为试件自重方向与荷载方向一致时测量的三点弯曲梁的荷载－挠度曲线；而试件实际的荷载－挠度曲线（考虑试件自重及附加在其上的设备重量）还包括图中的两段虚线[10～12].

图4 采用三点弯曲法确定混凝土断裂能示意图Fig.4 Determination of fracture energy of concrete by means of three－point bending method

传统意义上的混凝土断裂能Gf的计算公式：

其中A是韧带面积，A＝B（D－a0）；W是使三点弯曲梁完全断开时外力所做的功，其由4部分组成（考虑梁自重及其他附加重量的影响），如图4所示.

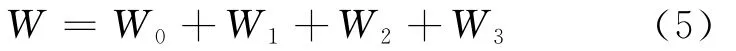
其中W0为荷载P所做的功，由式（6）确定；W1、W2和W3均为梁自重所做的功.W2、W3分别由式（7）和（8）确定，而W1非常小，可以忽略不计.

RILEM（50－FCM）推荐的断裂能的计算方法[16]是在假定W2＝W3的基础上进行的，即

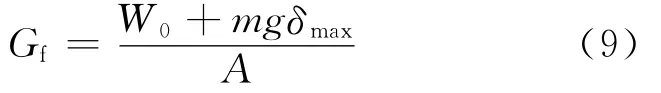
如图5所示，由于P－δ曲线下降段的尾部非常平缓，若测到荷载P降为零（即δ＝δmax）是非常耗时的，为提高试验效率，通常都取挠度δ＝δ0时作为停止试验的判断标准.通常为了得到较为准确的断裂能，需要对P－δ曲线下降段尾部的曲线进行修正.

图5 不同尺寸试件的P－δ曲线Fig.5 P－δcurves of different sizes of specimens

根据文献[10～12]的方法，本文采用幂函数对下降段尾部的曲线进行修正，取（Pmax＋mg）/3的荷载点为P－δ下降段曲线的反弯点，如图6所示.采用幂函数形式如下：

将式（10）代入式（8）积分

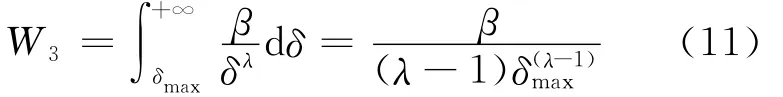
图6 P－δ尾部曲线的拟合Fig.6 Regression of P－δtail curve

但一般试验测试过程中很难得到δmax，为此需要对公式进行变换，即

由式（12）可见，当试验在δ＝δ0停止后，如果对δ0后的曲线进行适当的修正，可以得到细粒混凝土合理的断裂能，即

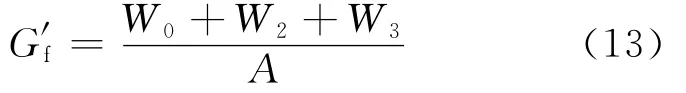
表3中给出对P－δ曲线下降段的尾部曲线进行修正后的计算结果.表4中给出式（9）和（13）计算结果，其中W0、W2和W3的计算是将式（6）～（8）中的δmax换为δ0.

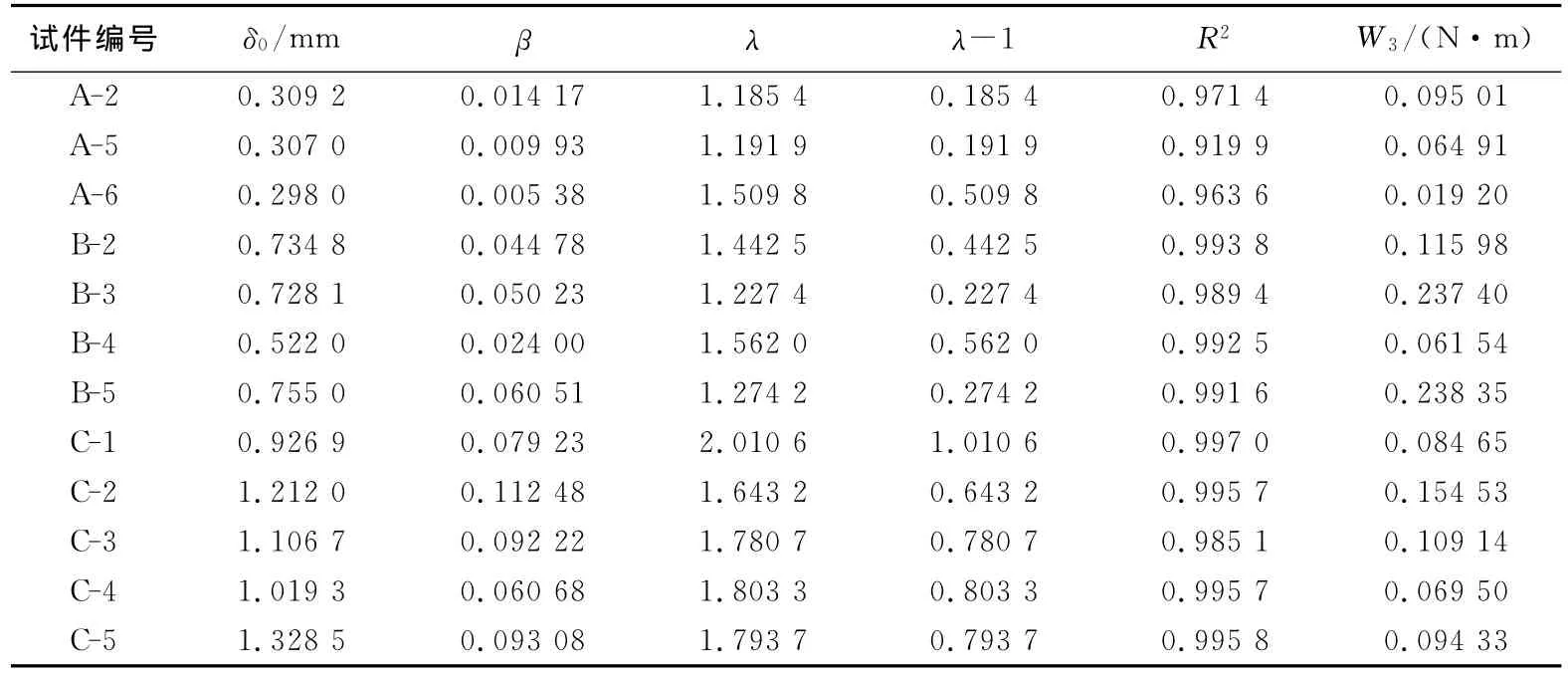
表3 拟合曲线参数值Tab.3 Values of fit curves

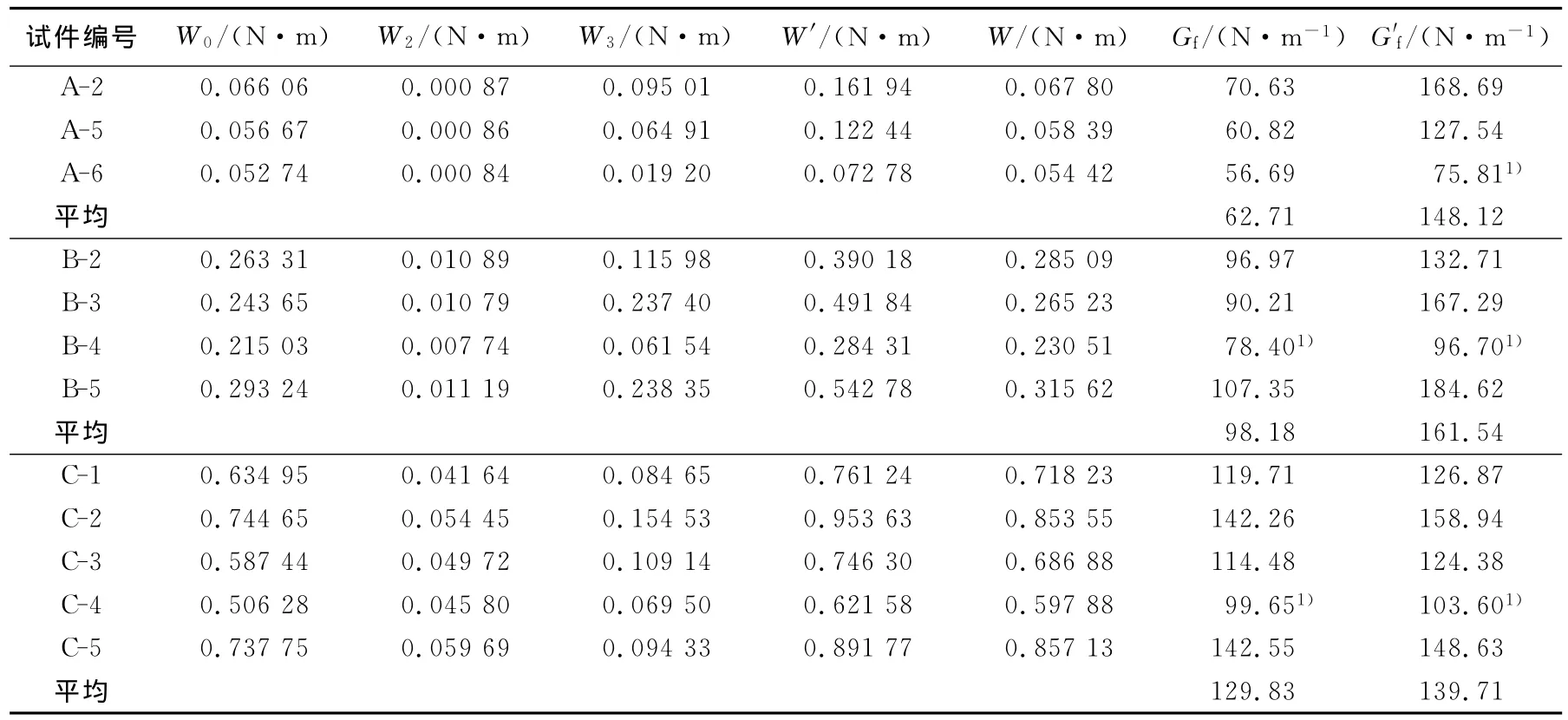
表4 试件断裂能Tab.4 The fracture energy of specimens

与断裂韧度平均值的计算相同，在断裂能的平均值计算时，也将与均值相差20%的个别值剔除，在计算均值时未计入其影响.

由表4中的计算结果可见，采用式（9）得到的计算结果具有明显的尺寸效应，而采用式（13）获得的计算结果可以认为在误差允许的范围内没有明显的尺寸效应，因分别由B和C系列试件获得的断裂能平均值与A系列试件获得的断裂能平均值148.12 N/m的差值都在15%以内.

结合文献[11]中的研究成果，将P（δmax）＝0.5mg代入式（10）可得

将式（14）代入式（11）可得

令

由表4的计算结果可知，当试件尺寸足够小，会有W2＜W3；然而随试件尺寸的增大，λ的值会逐渐变大，而k值会越来越接近1，即W2和W3的值越来越接近，从而断裂能的计算值与真实值差值变小，这也可由表4中的计算结果说明.当试件尺寸变化到某一值，会出现W2＝W3的这种情况；但当试件尺寸超过这一尺寸后，即λ＞2后，W2＞W3，若仍采用W2＝W3的假定，会导致随着试件尺寸的变大，断裂能的计算值将会有尺寸效应.

另一方面，在实际测试中，若试件尺寸太小，如A和B系列试件，P－δ下降段曲线的尾部比较平缓，从而δmax与δ0会有较大差值，这会导致W0和W2的计算值与实际值有一定的差别，从而断裂能的计算值和其真实值有较大的误差.当试件尺寸较大时，如C系列试件，P－δ的下降段尾部曲线变得较为陡峭，δmax值比较容易获得，这使得δmax与δ0差值几乎可以不考虑，因此断裂能的计算值和其真实值误差较小.

本文的这一研究结论与文献[9]通过对多组水泥砂浆和净浆的研究结论一致，研究表明：在试验误差允许的范围内，水泥砂浆和净浆的断裂能是一个与试件尺寸无关的材料参数.而关于普通混凝土的断裂能是否存在尺寸效应的问题一直有争议[10～12、17]，文献[11、17]认为断裂能是一个与试件尺寸有关的参数，文献[17]研究表明，即使对试验曲线进行尾部修正，断裂能还是随试件韧带高度的增加有上升的趋势；文献[10、12]则认为经过合理的计算处理，普通混凝土的断裂能可作为一个材料常数，与试件尺寸无关.

此外，文献[12]还指出断裂区以外的附加能耗随试件尺寸增大而变大是导致实测断裂能产生尺寸效应的根本原因，小尺寸的试件更适于获得试件的断裂能.而文献[17]指出混凝土试件在断裂破坏过程中，其实际断裂面并非是沿着计算断裂面进行的，而是曲折非直线形的，对于大韧带尺度试件，这种曲折形的影响将更为明显.

由此可知，本文细粒混凝土中没有粗骨料，且采用小尺寸试件，裂缝的发展路径比较规则，断裂区外的附加能耗较小，从而实测断裂能值与理论值比较接近，尺寸效应不明显.

4 结 论

细粒混凝土的裂缝扩展也存在一个断裂过程区，因此计算失稳韧度时需要考虑裂缝的实际扩展长度.小尺寸试件起裂韧度随着试件尺寸的增大而降低，有较明显的尺寸效应，这是由于小尺寸试件初始裂缝长度值和起裂荷载的测量值受试验因素的影响较大；而临界有效裂缝长度值和失稳荷载的测量值则相对准确，从而在误差允许的范围内失稳韧度的计算值不随试件尺寸而变化，几乎没有尺寸效应.由于试件类型有限，此问题还需要进一步的试验研究.

采用RILEM推荐的计算断裂能的方法得到的细粒混凝土的断裂能计算值受试件尺寸影响比较明显，这主要是由计算公式本身所致.但对P－δ的下降段尾部曲线进行合理修正后，得到的断裂能计算值几乎不随试件尺寸而变化，可作为一个材料常数.由于本文中的试件较少，对此结论还需要作进一步的理论分析和试验研究工作.

[1]徐世烺，李 赫.碳纤维编织网和高性能细粒混凝土的粘结性能[J].建筑材料学报，2006，9（2）：211－215

[2]HEGGER J，WILL N，BRUCKERMANN O，etal.Loading－bearing behavior and simulation of textilereinforced concrete [J].Materials and Structures，2006，39（8）：765－776

[3]BRUCKNER A，ORTLEPP R，CURBACH M.Textile reinforced concrete for strengthening in bending and shear [J].Materials and Structures，2006，39（8）：741－748

[4]PELED A. Confinement of damaged and nondamaged structural concrete with FRP and TRC sleeves[J].Journal of Composites for Construction，2007，11（5）：514－22

[5]BANHOLZER B， BROCKMANN T，BRAMESHUBER W.Material and bonding characteristics for dimensioning and modeling of textile reinforced concrete（TRC）elements [J].Materials and Structures，2006，39（8）：749－763

[6]BRAMESHUBER W，BROCKMANN T.Size effect on the mechanical properties of fine grained concrete matrices[C]//Proceedings of the 2nd Colloquium on Textile Reinforced Structures （CTRS2）.Dresden：Technische Universitt Dresden，2003：161－173

[7]BROCKMANN T. Mechanical and fracture mechanical properties of fine grained concrete for textile reinforced composites [D].Aachen：Institute of Building Materials Research，RWTH Aachen University，2006

[8]徐世烺，朱 榆，张秀芳.水泥净浆和水泥砂浆的I型断裂韧度的测定[J].水利学报，2008，39（1）：41－46

[9]XU Shi－lang，ZHU Yu.Experimental determination of fracture parameters for crack propagation in hardening cement paste and mortar[J].International Journal of Fracture，2009，157（s1－2）：33－43

[10]郭向勇，方坤和，冷发光.混凝土断裂能的理论分析[J].哈尔滨工业大学学报，2005，37（9）：1119－1222

[11]钱觉时，范英儒，袁 江.三点弯曲法测定混凝土断裂能的尺寸效应[J].重庆建筑大学学报，1995，17（2）：1－8

[12]张 东，刘娟淯，陈 兵，等.关于三点弯曲法确定混凝土断裂能的分析[J].建筑材料学报，1999，2（3）：206－211

[13]徐世烺，李 赫.用于纤维编织网增强混凝土的自密实混凝土[J].建筑材料学报，2006，9（4）：481－483

[14]XU Shi－lang，REINHARDT H W.A simplified method for determining double－Kfracture parameters for three－point bending tests [J].International Journal of Fracture，2000，104（2）：181－209

[15]吴智敏，徐世烺，王金来，等.三点弯曲梁法研究混凝土双K断裂参数及其尺寸效应[J].水力发电学报，2000（4）：16－24

[16]RILEM TCS.Determination of the fracture energy of mortar and concrete by means of three－point bend tests on notched beams [J]. Materials and Structures，1985，18（106）：285－290

[17]徐世烺，赵艳华，吴智敏，等.楔入劈拉法研究混凝土断裂能[J].水力发电学报，2003（4）：16－22