供热空调系统并联变频水泵转速比配置优化分析
2011-06-05赵天怡,张吉礼,马良栋
赵 天 怡, 张 吉 礼, 马 良 栋
(大连理工大学 建设工程学部 土木工程学院,辽宁 大连 116024)
0 引 言
供热空调系统能耗是建筑能耗的重要部分.对于大型公共建筑,供热空调系统电耗的60%~70%被以水泵与风机为主的能量输配系统所消耗,其中水泵的节能潜力更明显.变频技术是水泵节能控制的主要实施手段,水泵转速通常参考水系统压差进行调节,对于某一压差设定值,末端用户流量需求增加时,要求水泵转速也随之提高.对于变流量空调系统中的各用户末端,个性化的流量调节要求系统提供较宽的流量可调范围,即需要多台水泵同时并联运行.在并联水泵变频运行方面,诸多学者进行了多方面的研究:文献[1、2]参考水泵效率与转速的关联式,在定压差控制模式下研究了获得水泵最优效率的水泵转速值,并应用于并联变频水泵的优化控制中.文献[3]针对变水量系统中的二次泵控制问题,利用技术经济法分析了并联变频水泵控制策略的节能性.文献[4]比较了并联水泵非同步变速控制与同步变速控制的应用效果,在工况可调性、节能性与安全性方面,指出同步变速控制要优于非同步变速控制.文献[5]仿真比较了并联水泵一台定速、一台变速控制与两台同时变速控制性能,并分析了背压与流量对水泵性能的影响情况.
可见,在肯定并联变频水泵控制的节能效益的同时,在控制策略实施的过程中,一些细节问题如多台水泵同步变频时转速如何优化搭配值得深入探讨.从研究手段上看,多数文献采用代表性的仿真算例,通过比较各策略的应用效果研究并联水泵变频控制中的相关问题,但缺乏必要的理论分析过程,因此较难得到普适性的结论.
为此,本文借助于变频水泵性能模型,结合理论分析与仿真算例,研究供热空调系统并联水泵变频运行工况下各水泵转速的最优化配置问题.
1 变频水泵的特性模型
定义转速比为水泵当前转速与额定转速的比值,用w表示.在水泵额定转速运行状态下,即w=1,水泵扬程、效率及功率可分别通过式(1)、(2)与(3)计算得到.
对于暖通空调系统中应用的水泵,其性能曲线形状较平坦,在具备一定数量的性能拟合数据的前提下,利用如式(1)、(2)所示的多项式形式可以保证拟合的精度.
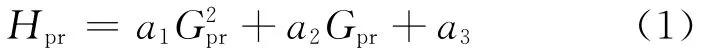
式中:Hpr代表水泵额定转速下的扬程,m;Gpr代表水泵额定转速下的流量,m3/s;a1、a2、a3为性能常数,由样本数据或实测数据拟合得到.由于a1<0,式(1)表示的二次函数曲线形状为上凸型;a3代表流量为0时的水泵扬程,a3>0;由于Gpr相比于Hpr很小,a1的绝对值远大于a2与a3的绝对值.
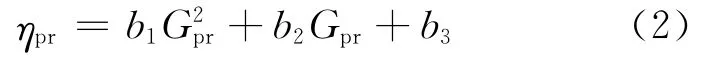
式中:ηpr代表水泵额定转速下的效率,%;b1、b2、b3为性能常数,由样本数据或实测数据拟合得到.由于b1<0,式(2)表示的二次函数曲线形状为上凸型;当Gpr=-b2/2b1时,ηpr极大,设该点(即水泵最佳工作点)流量为Gb,对于每台水泵的流量变化范围内,均存在Gb,即b2>0.
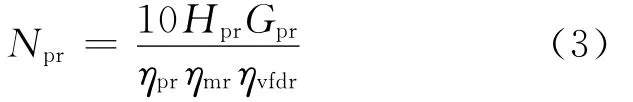
式中:Npr代表水泵额定转速运行状态下的功率,k W;ηm代表电机效率,%,与w相关;ηvfd代表变频器效率,%,与w相关;ηmr、ηvfdr分别代表水泵额定转速下(w=1)的电机效率(%)与变频器效率(%).
图1为额定转速工况与变速工况下的水泵性能曲线对比情况,可见,当水泵处于变速工况(w<1)时,可利用相似工况曲线建立变速工况下与额定转速工况下扬程 -流量曲线间的联系,如下式所示:
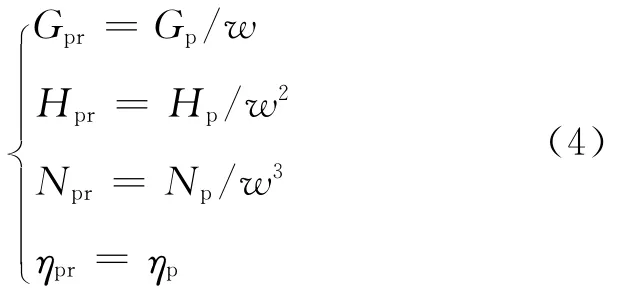
式中:Gp代表变速工况水泵流量,m3/s;Hp代表变速工况水泵扬程,m;Np代表变速工况水泵功率,k W;ηp代表变速工况水泵效率,%.
将式(4)代入式(1)~ (3)中,可得变频工况水泵特性模型如下:

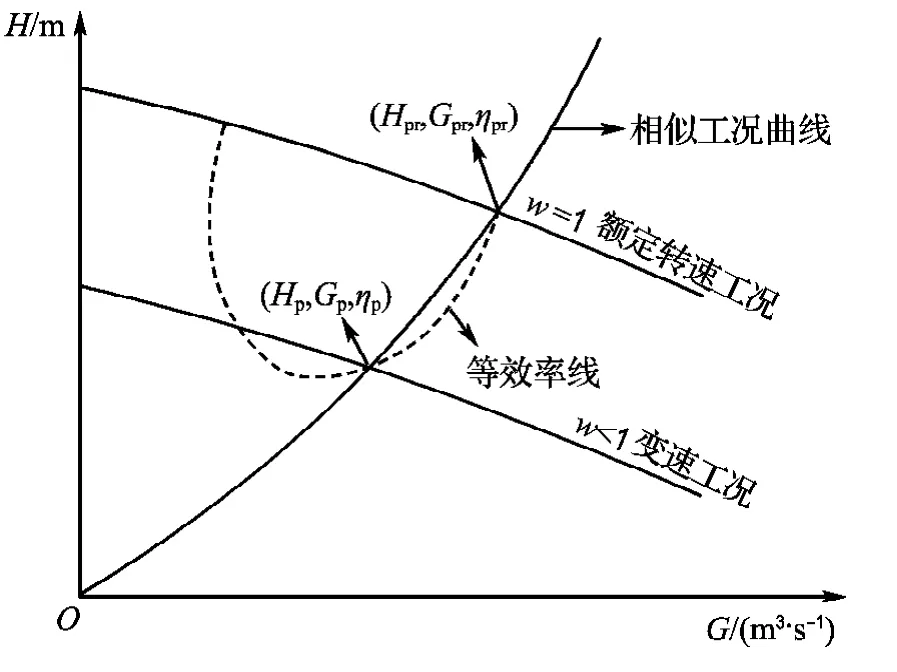
图1 额定转速工况与变速工况的水泵性能曲线Fig.1 Pump performance curves at rated condition and variable speed condition
2 理论分析
设m台同型号的水泵并联变频运行,系统要求并联水泵提供扬程为Hr、流量为Gr的水力工况.设第i(1<i<m)台水泵的转速比、流量、扬程、水泵效率、电机效率与变频器效率分别为w i、Gpi、Hpi、ηpi、ηmi、ηvfdi,并联水泵的总功率可由下式计算得到:
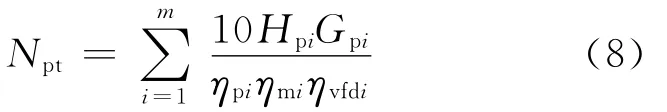
由并联水泵流量与扬程特性可知如下约束条件:
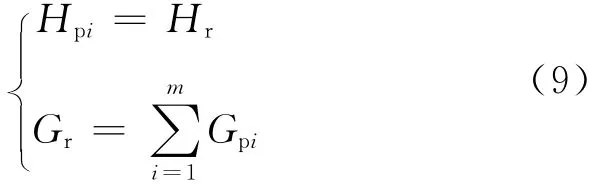
根据式(9)的约束条件,Npt可改写为
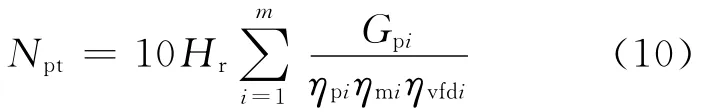
由式(10)可以明确,并联变频水泵转速比的优化配置目标为Npt,约束条件为式(9).优化思路可简单描述为如何配置各水泵转速比,在实现同一水力工况点的前提下,消耗最小的Npt.
由式(10)可知,对于并联水泵中的任意一台
水 泵i, 如 果Gpi/ηpiηmiηvfdi取 得 极 小 值,也为极小,即Npt为最小,优化目标可转化为Gpi/ηpiηmiηvfdi.文献[6]表明,转速比是决定ηm与ηvfd的唯一参数,当0.4<w<1.0时,w对ηm与ηvfd影响较小:ηm范围为[92%,94%],ηvfd范围为[83%,95%];当w<0.4时,w对ηm与ηvfd有较大影响.因此,若设定转速比低限为0.4同时转速变化幅度不大时,可认为ηm与ηvfd不变.因此,优化目标可简化为Gpi/ηpi.
对于任意两台水泵i与j,结合式(6),有
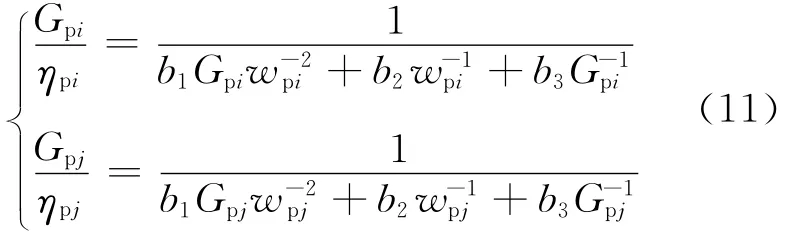
式中:Gpi/ηpi与Gpj/ηpj同时取得极小值的条件为式右侧分母同时取得极大值.即b1GpiWi2+b2Wi+b3Gp-i1取得极大值(Wi=wp-i1),满足极值条件的Wi可表示为 -b2/2b1Gpi,即有
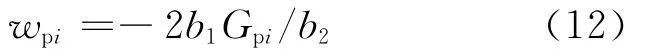
将Gb=-b2/2b1代入式(12)得

即当式(13)成立时,Gpi/ηpi达到极小值.参考wpi变化范围,分析如下工况:
(1)当Gpi≤Gb时,wpi≤1.0,符合转速比的实际范围,对应Gpi/ηpi极小值的wpi取值为-2b1Gpi/b2.同理,当Gpj≤Gb时,对应Gpj/ηpj极小值的wpj取值为-2b1Gpj/b2.结合式(5)与式(9),有
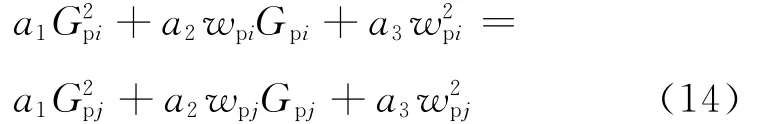
将wpi=-2b1Gpi/b2,wpj=-2b1Gpj/b2代入式(14),整理得
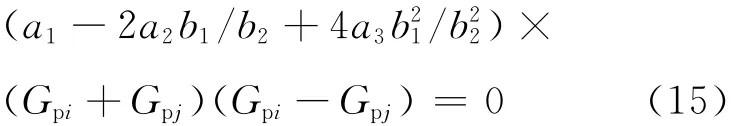
因此,式(15)成立的条件为Gpi=Gpj,由式(5)与式(9)可知wpi=wpj.由于Npt达到极小值的条件为式(15)成立,即wpi=wpj时,Npt取得极小值.
(2)当Gpi>Gb时,wpi>1.0,超出转速比的实际范围,对应Gpi/ηpi极小值的wpi取值为1.0.同理,当Gpj>Gb时,对应Gpj/ηpj极小值的wpj取值为1.0.
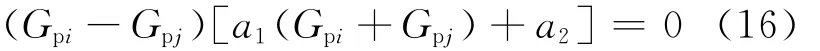
将wpi=1.0,wpj=1.0代入式(14),整理得设C2=a1(Gpi+Gpj)+a2,由于a1的绝对值要远大于a2的,即使a1乘以(Gpi+Gpj)这样一位小数级的正数,其绝对值仍要大于a2,因此无论a2是正是负,C2均不存在为0的可能.
因此,式(16)成立的条件为Gpi=Gpj,由式(5)与式(9)可知wpi=wpj.由于Npt达到极小值的条件为式(16)成立,即wpi=wpj时,Npt取得极小值.
(3)当Gpi≤Gb时,wpi≤1.0,符合转速比的实际范围,对应Gpi/ηpi极小值的wpi取值为-2b1Gpi/b2.当Gpj>Gb时,对应Gpj/ηpj极小值的wpj取值为1.0.
将wpi=-2b1Gpi/b2,wpj= 1.0,Gb=-b2/2b1代入式(14),整理得
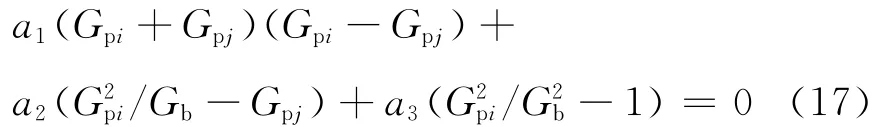
分析式(17)的各部分,由于a1的绝对值要远大于a2与a3,即便a1、a2和a3与目前对应的数相乘,式(17)的第1部分的绝对值也要远大于第2部分与第3部分.
因此,可知式(17)成立的条件为Gpi=Gpj=Gb,由于Gpj>Gb,该工况下Gpi/ηpi与Gpj/ηpj无法同时达到极小值.
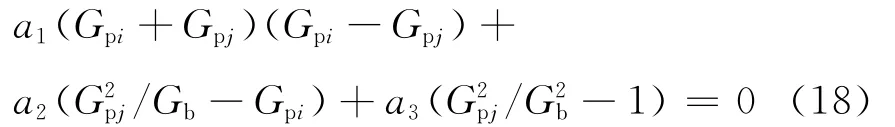
由a1、a2、a3的大小关系可知式(18)成立的条件为Gpi=Gpj=Gb,由于Gpi>Gb,该工况下Gpi/ηpi与Gpj/ηpj无法同时达到极小值.
综上所述,对于并联变频水泵的任意两台水泵,在同一系统水力工况下,两台水泵转速比相同,即意味着所有并联水泵转速比均相同的情况下,并联水泵总功率为最小.
(4)当Gpi>Gb时,wpi>1.0,超出转速比的实际范围,对应Gpi/ηpi极小值的wpi取值为1.0.当Gpj≤Gb时,对应Gpj/ηpj极小值的wpj取值为-2b1Gpj/b2.
将wpi= 1.0,wpj=- 2b1Gpj/b2,Gb=-b2/2b1代入式(14),整理得
3 算例仿真
仿真对象选取某变流量空调水系统,其采用两台并联冷冻水泵,a1、a2、a3分别为-1308.19、-50.9、78.61;b1、b2、b3分 别 为 -124.6、21.2、-0.2.水泵转速采用压差控制模式,压差监测点位于供、回水干管间,压差设定值根据最不利热力环路进行实时优化设置[7].选取空调季某工作日的51组系统仿真工况,工况参数包括冷冻水泵扬程与冷冻水干管流量,如图2所示.考察的仿真方案如下:
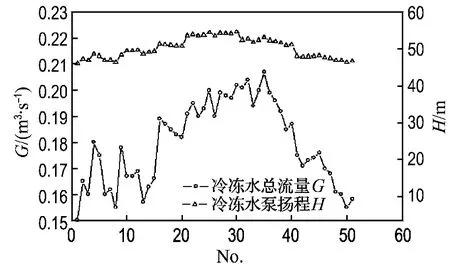
图2 仿真工况Fig.2 Simulated condition
方案1 一台泵全速运行,一台泵变频运行.该方案对应如下的水泵控制策略:控制器先启动一台水泵,根据压差设定值与压差监测值的偏差调节单台水泵的转速,当单台水泵全速运行但仍不能满足压差设定值的要求时,启动第二台水泵,调节其转速以维持压差设定值.
方案2 两台泵同时变频运行,两台泵的转速比相差0.05.两台水泵采用不同的频率调节算法,即对应同一压差偏差,控制器输出不同的频率信号至两台水泵的变频器.为简化分析,设定两台泵的转速比之差Δw恒为0.05.
方案3 两台泵同时变频运行,两台泵的转速比相差0.1.同方案2,设定两台泵的转速比之差恒为0.1.
方案4 两台泵同时变频运行,转速比相同.两台水泵采用同一频率控制信号,即转速比相同.之前的理论分析表明,对应同一水力工况点,此方案的水泵总电耗最低.
仿真的目标参数主要为水泵总功率,如图3所示.各仿真方案的水泵性能参数平均值如表1所示.仿真结果表明:
(1)由图3可见,方案1~4的水泵总功率平均值分别为226.2、152.7、167.5、148.2 k W.在同一水力工况下,方案1的水泵电耗最高,方案4的水泵电耗最低.比较方案2、3与4的仿真结果可知:并联水泵的转速比越接近,水泵的节能性越好,这与理论分析得到的结论是一致的.
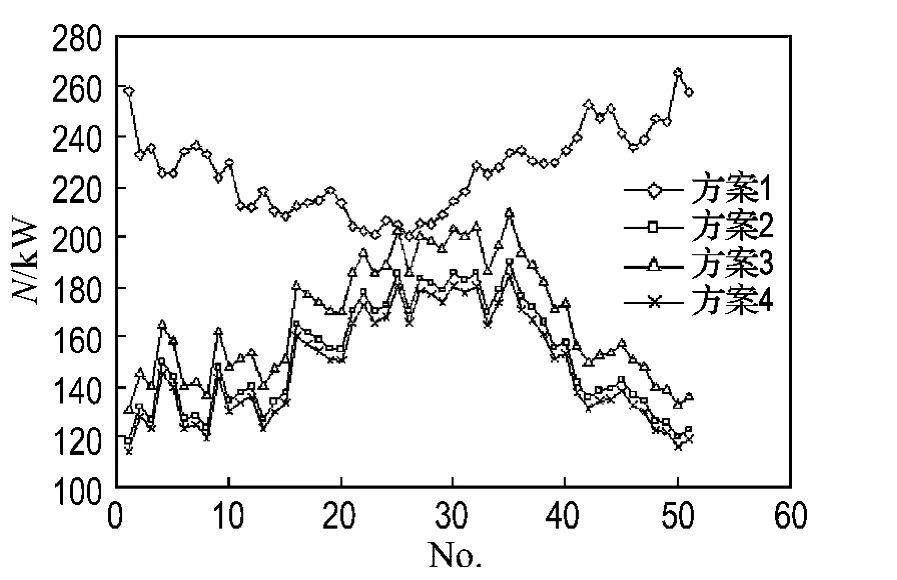
图3 冷冻水泵总功率仿真结果Fig.3 Simulation result of total power of chilled water pump
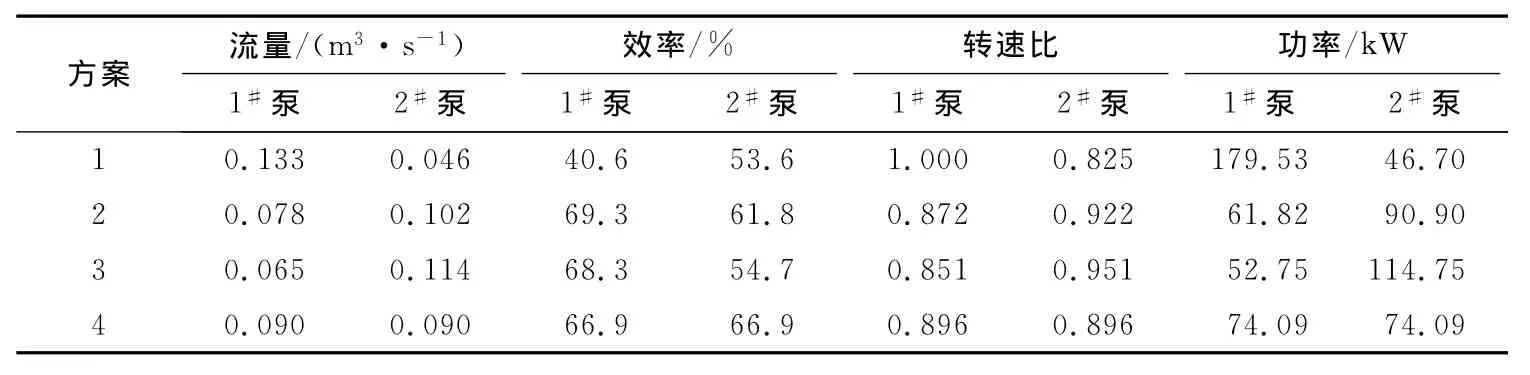
表1 仿真方案对应的水泵性能参数平均值Tab.1 Average value of simulated pump performance parameters
(2)影响水泵总电耗变化的因素可归结于两方面,即水力工况与水泵效率.对于水泵同时变频的方案2~4,由于水泵效率随水力工况的变化不大(48%~70%,图4),因此主导水泵电耗的因素为水力工况,对比图2与图3可知,在仿真工况内扬程变化幅度相比于流量变化幅度较小,因此流量的变化趋势决定了水泵电耗的变化趋势,即当流量升高时,水泵电耗增加.
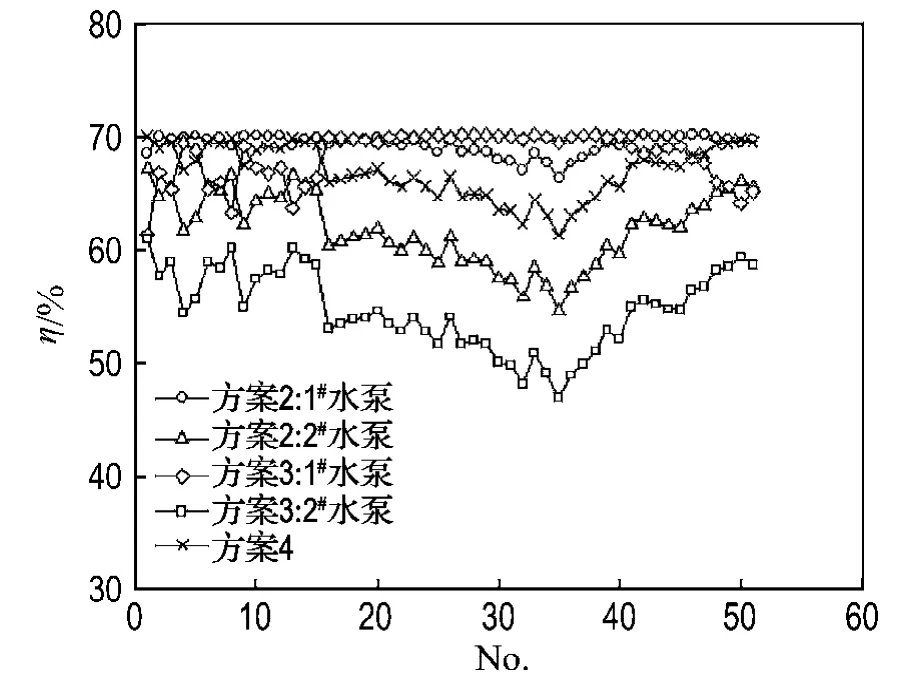
图4 两台水泵转速比差对冷冻水泵效率的影响情况(方案2~方案4)Fig.4 Pump efficiency vs.speed ratio difference of two pumps(Scheme 2 -Scheme 4)
方案1在仿真工况内的水泵效率变化范围较大(11%~70%,图5),当流量较小时,由于两台水泵的流量分配悬殊,变频水泵的效率非常低;当流量逐渐提高时,两台水泵的流量分配逐渐均匀,变频水泵的效率不断增加.因此,由水力工况变化而引起的水泵效率波动对水泵电耗的影响程度要大于水力工况本身对水泵电耗的影响程度,即对应较小的流量需求,水泵电耗反而增加(对比图2与图3).
(3)对比图5中的转速比差变化与两台水泵功率的变化趋势可知,当两台水泵的转速比越接近时,两台水泵的效率就越高(转速比差从0.21降至0.11时,第一台水泵效率由36%升至50%;第二台水泵效率由11%升至70%).转速比的差异代表着两台水泵流量分配的均匀性即两台水泵工作点在性能曲线图中的接近程度,两台水泵的工作点相距越远,则表明两台水泵的工作点流量偏离当前转速下的Gb的可能性越大,即两台水泵或其中一台水泵的效率将处于较低的水平,从而影响水泵的总体节能效果.
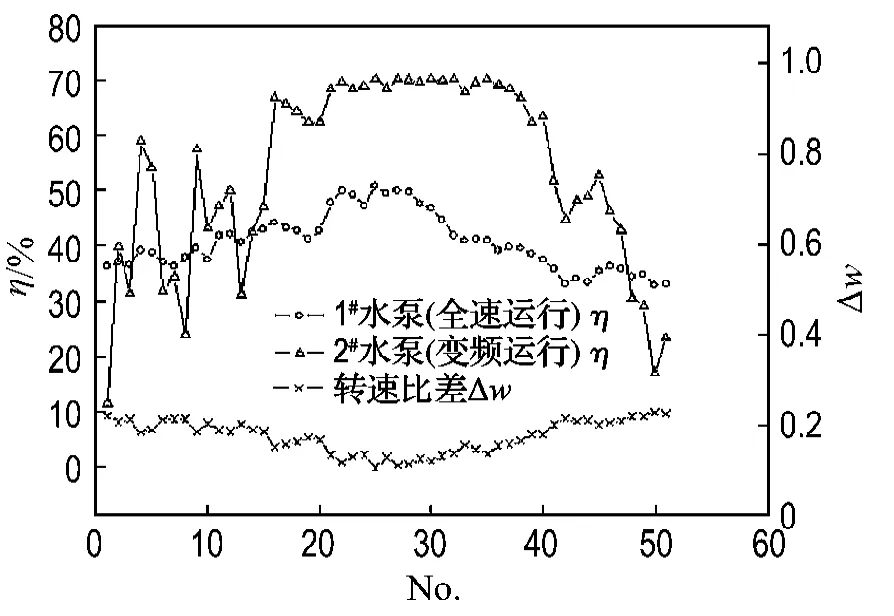
图5 冷冻水泵效率及两台水泵转速比差(方案1)Fig.5 Pump efficiency vs.speed ratio difference of two pumps(Scheme 1)
4 结 论
(1)在相同的水力工况下,并联变频水泵同转速比运行时,水泵将获得最优的节能效果.
(2)仿真算例结果表明(表1),以一台水泵全速运行、一台水泵变频运行策略的水泵电耗为基准,双泵以相同转速比变频运行策略的水泵节能量为34.5%.
(3)影响水泵总电耗变化的因素有两方面:水力工况与水泵效率.当转速比差在一定范围内时,影响水泵总电耗的是水力工况.当转速比差较大时,水泵间的转速比差影响各水泵的流量分配,进而影响各水泵的效率,此时影响水泵总电耗的主要因素是转速比差.
[1]SZYCHTA L.System for optimising pump station control[J].World Pumps,2004(449):45-48
[2]SZYCHTA L.System for optimising pump station control-PartⅡ [J].World Pumps,2004(454):32-34
[3]李建兴,涂光备,涂岱昕.多泵并联空调水系统的技术经济分析[J].流体机械,2004,32(10):38-41,31
[4]胡思科,吕 太,柏静儒.开式系统并联水泵非同步调速运行时的能耗分析[J].流体机械,2004,32(3):28-31
[5]许光映.变频调速并联水泵系统性能仿真研究[J].暖通空调,2007,37(3):49-53
[6]BERNIER M A,BOURRET B.Pumping energy and variable frequency drives [J].ASHRAE Journal,1999,41(12):37-40
[7]赵天怡,张吉礼,孙德兴.基于最不利热力环路的变流量空调水系统压差重整化方法[J].暖通空调,2009,39(5):56-61
