基于压缩感知的弹道导弹微多普勒提取方法

李 松 朱 丰 刘昌云 冯有前 张 群

（1空军工程大学导弹学院，陕西 三原 713800）（2空军工程大学电讯工程学院，陕西 西安 710077）

1.引 言

随着弹道导弹技术的发展，弹道导弹的攻防对抗日益激烈。对弹道导弹防御来说，关键是目标识别，也就是说能否从诱饵中识别出真弹头［1］。高速、隐身、干扰等技术手段的应用增加了弹头识别的难度。对于弹道导弹目标，雷达识别大致有三个途径［2－3］：一是表面材料特征识别；二是结构形状特征识别；三是运动特征识别。随着电磁控制技术的发展和诱饵制作水平的提高，使得基于表面材料特征和结构形状特征的弹头和诱饵的可分性降低，而由于有效载荷的限制，诱饵和弹头的质量分布特征不同，质量分布特征不同会导致运动特征不同，因此，运动特征是弹道导弹目标识别的主要依据［4］。弹道导弹目标运动特征包括轨道运动特征和微动特征。弹头和诱饵之间的轨道特征差异不大，而微动特征差异较大，因此，识别弹头和诱饵应充分利用它们的微动特征的差异。平动产生多普勒，微动产生微多普勒［4－5］。通过微多普勒可以提取弹道导弹目标的微动特征，利用弹头和诱饵微动特征的差异可识别出真弹头。

近年来，微动及微多普勒逐渐得到国内的广泛关注。文献［6］分析了锥形目标的锥旋模型及其微多普勒。文献［7］－［8］分析了锥形弹头的进动模型及其微多普勒。文献［9］分析了锥形弹头的章动特性及章动频率的提取方法。文献［10］分析了微多普勒的一些工程问题，指出微多普勒与载频和带宽的关系。载频越高，微多普勒越大，越利于检测和提取；带宽越宽，越利于解决多散射点的微多普勒问题，越利于真假弹头识别。但是带宽越宽，对回波信号的采样速率就越高，这对算法和硬件提出了更高的要求。如何能以较低的速率采样回波信号，提取微多普勒，以进一步识别真假弹头呢？

近年来出现了一种新的信号获取与压缩重构方法－压缩感知（CS）［11－12］，它的优势在于非自适应（Non－Adaptivity）的，能够突破采样定理的极限；抗干扰性也较强，压缩后的信号中即使丢失了某几项，仍然可以完美地重构原始信号。CS理论在信号提取、特征识别等领域中都有着广泛的应用前景。文献［13］研究了对回波信号稀疏采样后进行匹配滤波的方法，证实了利用CS理论可恢复并合成距离像。文献［14］研究了在任意冗长频带的条件下，利用CS理论对稀疏子孔径进行拼接处理并成像。文献［15］研究了目标处于复杂的电磁背景环境下，利用CS理论分析目标的多静态电磁散射特性。文献［16］研究了CS理论在超宽带雷达成像中的应用。

对于CS理论在弹道导弹微多普勒效应研究及提取方面的应用，国内的报道较少。本文详细分析了弹道导弹的微动模型，给出了弹道导弹目标的微多普勒计算公式，给出了利用CS理论重构弹道导弹微多普勒的方法。利用CS理论从回波信号中提取了弹道导弹的微多普勒，与从回波信号中提取的微多普勒和理论上计算的微多普勒是一致的，这表明在载频较高和回波信号带宽较宽的情况下，以较低频率采样弹道导弹回波信号，提取弹道导弹的微多普勒，以降低工程实现难度的方法是可行的、有效的。

2.弹道导弹微动模型

2.1 弹道导弹微动形式分析

弹道导弹目标可以通过旋转进行空间定向，也可以依靠弹上的动力装置进行空间定向。弹道导弹目标的运动过程可以分为助推段、中段、再入段。在不同阶段，弹道导弹目标所采用的定向方法是不同的，导弹的运动特征（轨道特征和微动特征）也是不同的。

在助推段，弹道导弹运动的动力来自动力装置，导弹的运动特征主要表现为轨道特征，微动特征不明显。弹头和舱体分离后，弹头进入中段惯性滑行阶段。弹头中段的定向方法通常是自旋。在中段，弹头受到的力只有重力，如果重力的作用点与弹头质心重合，则重力矩为零，根据角动量守恒定理，弹头的微动只表现为自旋，也就说弹头绕对称轴做旋转运动。如果重力的作用点与弹头的质心不重合，则重力矩不为零，弹头的微动表现为“自旋”＋“锥旋”，锥旋是指弹头绕对称轴以外的某空间轴线的旋转运动，“自旋”＋“锥旋”就是进动。在弹头分离的时候，如果受到其他力的干扰，弹头可能会出现章动，也就是进动角（锥旋轴与自旋轴的夹角）变化的进动。章动不是一种稳定的微动形式，它只是进动在受到其他力干扰时才表现出的微动形式。根据角动量守恒定理，一旦外力撤销，章动现象会慢慢减弱，章动逐渐变为进动。

当弹头返回大气层时，进入再入段。在再入段，弹头的微动依然表现为进动，但是进动参数相对中段来是有所变化，变化的原因是在再入段重力矩减小了。

2.2 自旋模型

弹道导弹目标自旋时，其与雷达的几何关系如图1所示。

图1 弹道导弹锥形弹头的自旋模型

（U，V，W）为雷达坐标系，其坐标原点为O，雷达位于O点。（x，y，z）为目标本地坐标系，也称为弹体坐标系［10］，其坐标原点为目标的质心O′，O′z轴为目标对称轴，也是自旋轴，本地坐标系随弹头的运动而运动。（X，Y，Z）为参考坐标系，其坐标原点P0位于O′z轴，一般情况下，取自旋轴与锥旋轴的交点为参考坐标系的原点，参考坐标系（X，Y，Z）与雷达坐标系 （U，V，W）平行，只随弹头的平动而运动。P0点在本地坐标系中的位置矢量r0＝ （0，0，z0），在雷达坐标系中的方位角和仰角分别为α和β，到雷达的初始距离矢量为R0.

设P点在本地坐标系中的初始位置矢量为rp＝（xp，yp，zp），则其在参考坐标系中的初始位置矢量为

式中Rinit为初始旋转矩阵，也就是初始时刻本地坐标系到参考坐标系的旋转矩阵。

t时刻P点在参考坐标系中的位置矢量为

式中Tspining为弹头在参考坐标中的自旋矩阵，则t时刻P点在雷达坐标系中的位置矢量为

式中v是弹头平动的速度矢量，如果知道Rinit和Tspining，就能求出R（t），根据发射信号和R（t），能得到P点回波信号的相位，进而得到回波信号的多普勒和微多普勒。

参考坐标系中的Tspining为

Esr为自旋轴单片向量esr的叉乘矩阵。

Rinit可用式（5）～ 式（8）计算。

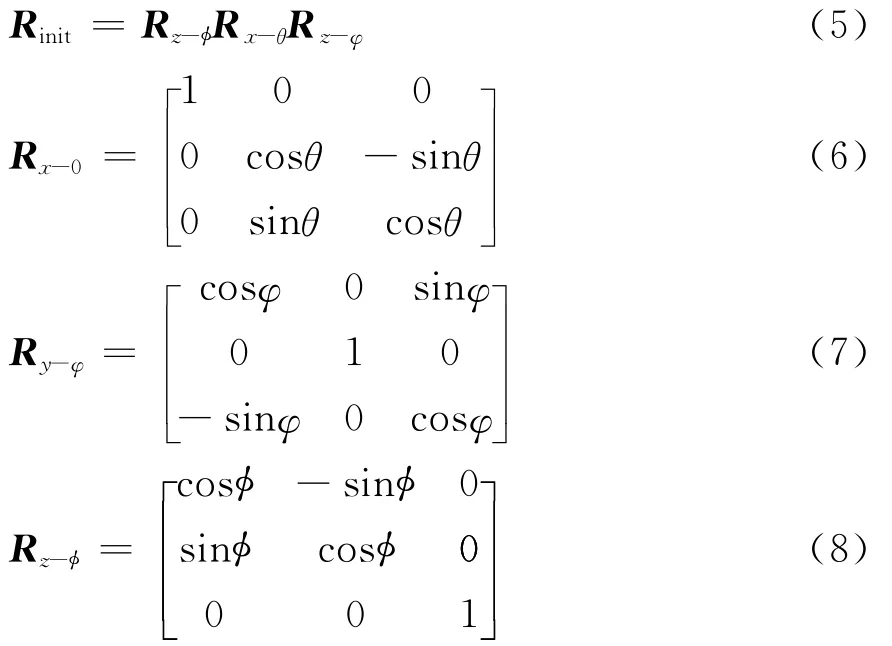
式（5）～ （8）中（φ，θ，φ）称为初始欧拉角。

2.3 进动模型

弹头进动时，其与雷达的几何关系如图2所示。

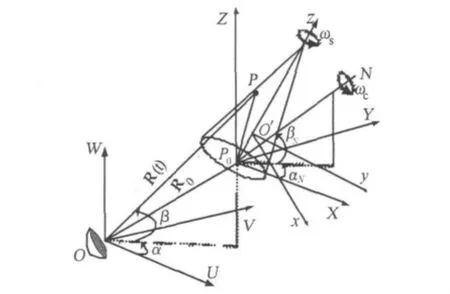
图2 弹道导弹锥形弹头的进动模型

O′z为自旋轴，弹头绕O′z以角速率ωs做自旋运动；P0N为锥旋轴，弹头绕P0N以角速率ωc做锥旋运动。P0N与自旋轴O′z的交点为P0，为简单起见，将P0点做为参考坐标系P0XYZ的原点。P0N在P0XYZ中的方位角和仰角分别为αN和βN，其在P0XYZ中的轴向单位向量ecr可表示为

t时刻P点在参考坐标系中的位置矢量为

式中Tprecession为弹头在参考坐标中的进动矩阵，可表示为

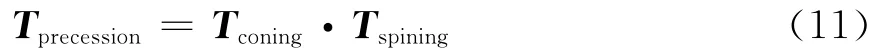
根据自旋矩阵的推导原理，可得

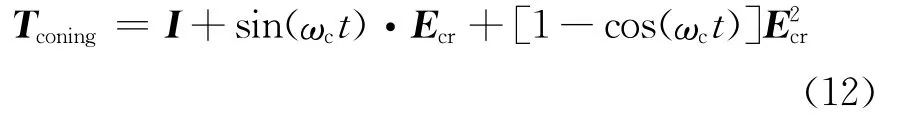
式中，Ecr为锥旋轴单位向量ecr的叉乘矩阵。

2.4 章动模型

弹头绕对称轴的旋转称为自旋；弹头在绕对称轴自旋的同时绕空间某轴旋转的运动称为进动，进动可以理解为“自旋”＋“锥旋”；一般情况下，进动角是固定不变的，进动角变化的进动称为章动，章动可以理解为“自旋”＋“进动角变化的进动”。章动矩阵可用式（13）来描述。

式中Tconing＝I＋sin（ωct）·Ecr（t）＋［1－cos（ωct）］）.

3.弹道导弹微多普勒

由于篇幅所限，主要分析弹道导弹目标进动的微多普勒。

假设雷达发射的是单频信号，载频为fc，根据式（10）和式（11），雷达回波信号的瞬时频率为

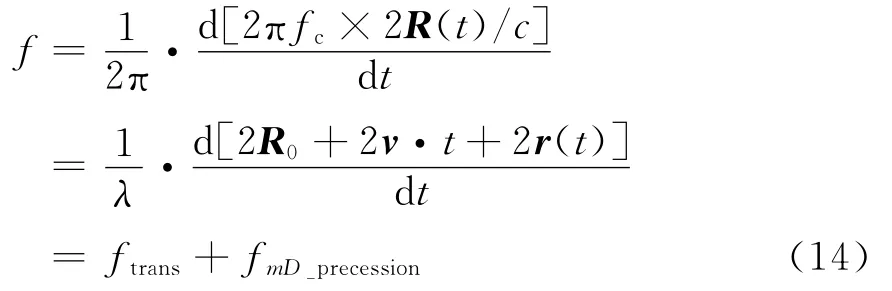
式中：c为光速；λ为信号波长；ftrans为弹头平动产生的多普勒；fmD－precession为弹头进动产生的微多普勒，则fmD－precession表示为

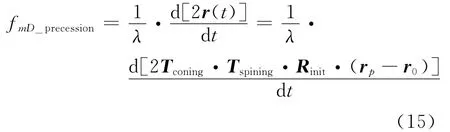
4.压缩感知基本原理

只要信号是可压缩的或在某个变换域是稀疏的，那么就可以用一个与变换基不相关的观测矩阵将所得高维信号投影到一个低维空间上，然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号［17］。在该理论框架下，采样速率不决定于信号的带宽，而决定于信息在信号中的结构和内容。压缩采样与重建的一般过程如图3所示。

求出信号X在该稀疏域上的表征形式Θ＝ΨTX，Θ是信号X在稀疏域Ψ的稀疏表示，两者是等价的。

2.2 两组肠道功能比较 复苏后，观察组患者 在肠道功能恢复时间、腹部体征消失时间方面均优于对照组，差异有统计学意义（P＜0.05），见表2。

设计一个与稀疏基Ψ不相关的M×N维的观测矩阵Φ，将高维信号X进行非自适应的线性观测，投影到一个低维空间上，得到观测数据

在一定条件下，将0－范数条件下的N－P难题转化为1－范数意义下的最优化求解问题，求解X的精确值或近似逼近.使所求得的近似向量X在Ψ基上的表示是最稀疏的。

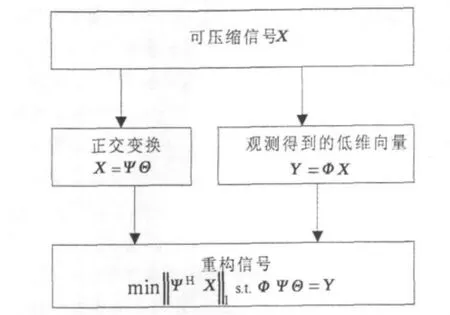
图3 基于压缩感知的采样与重建

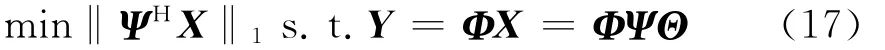
l1最小范数下最优化问题可化简为一个线性规划问题，其常用算法包括凸松弛算法、组合算法和贪婪追踪算法三个大类。其中，凸松弛法是将非凸问题转化为凸优化问题求解找到信号的逼近，如BP算法、内点法等；组合算法要求信号的采样支持通过分组测试快速重建，如傅里叶采样、链式追踪等。凸松弛法虽然重建结果十分准确，但计算负担很重；组合算法速度快，但没有凸松弛法运算结果准确。而贪婪追踪算法则是在运行时间和采样效率上都位于上述两类算法之间的，通过每次迭代时选择一个局部最优解来逐步逼近原始信号，比较常见的算法有匹配追踪法（MP）和正交匹配追踪法（OMP）等。

5.基于压缩感知的微多普勒重构方法

基于以上分析，本文提出利用压缩感知理论来提取微多普勒信息，其具体步骤如下：

第一步：获得含有微多普勒信息的雷达原始回波模拟信号s（t），t∈ （0，T），其中T为回波总时间。

第二步：定义时间分辨率τ，即窗长，并利用基于该窗长的矩形窗对含有微多普勒信息的原始回波信号进行滑动加窗处理，其中，滑动次数MN＝［T／τ⏋，［·⏋为向负无穷大取最小整数；可获得各次加窗后的模拟信号s′i（t），i＝1，…，NN.

第三步：构造非相关测量器Φ，并对各次滑动加窗处理后的结果s′（t）依据公式（16）进行非相关测量采样，以低采样速率获得各次低维的观测序列m1（n）＝Φ＊s′i（t），n＝1，…，M，M为低维观测数，“＊”表示测量处理过程。

第四步：对各次低维的观测序列mi（n）依据公式（17）进行重构处理，获得各次重构结果（n），i＝1，…，NN，n＝1…，N，N为利用奈奎斯特采样定律获得的采样个数。

第五步：将各次重构结果依次排列S＝（n），（n），…，（n）］，即为最终的微多普勒提取结果。

其步骤可如图4所示。

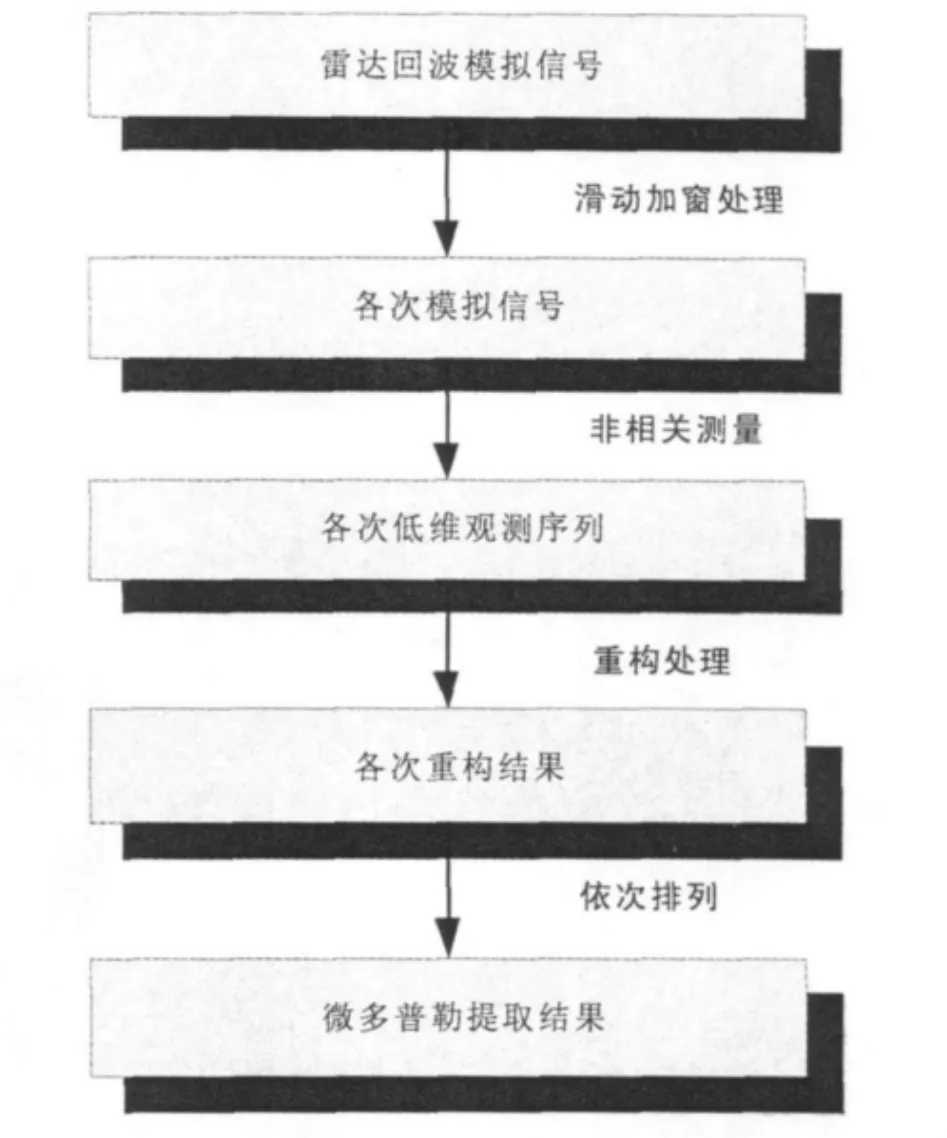
图4 基于压缩感知的重构微多普勒流程

6.仿真验证

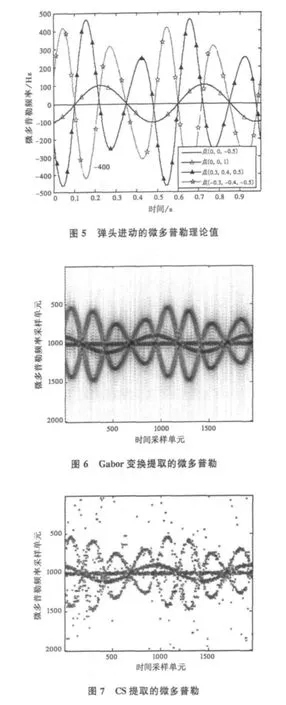
弹头进动模型如图2所示，长度单位为米。锥形弹头高2，弹头半径0.5；参考坐标系P0XYZ的坐标原点P0在雷达坐标系中的初始位置为（2000，9000，8000），P0在本地坐标系O′xyz中的坐标为（0，0，－0.5），O′xyz相对于P0XYZ的初始欧拉角为（45°，20°，30°）。弹头绕O′z自旋，同时绕P0N锥旋，锥旋轴P0N在P0XYZ中的方位角αN和高低角βN分别为60°和45°，自旋角速度ωs和锥旋角速度ωc分别为8πrad／s和4πrad／s.雷达载频为5 GHz，脉冲重复频率为2000Hz，带宽为1GHz.取弹头上点（0，0－0.5）、（0，0.1）、（0.3，0.4，0.5）和（－0.3，－0.4，－0.5），理论上的微多普勒如图5所示，利用Gabor变换从回波信号提取的微多普勒如图6所示，利用CS理论提取的微多普勒如图7所示。

7.结 论

利用微多普勒识别真假弹头的关键是微多普勒的提取。较高的载频和较宽的回波信号带宽有利于微多普勒的提取和微动特征识别。但是带宽越宽，对回波信号的采样速率就越高，这对算法和硬件提出了更高的要求；同时载频高，也会带来微多普勒模糊的问题。如何能以较低的速率采样回波信号，提取微多普勒，以进一步识别真假弹头呢？CS理论是个很好的选择。论文将压缩感知方法应用到宽带雷达回波信号的微多普勒提取中，并给出了弹道导弹目标的微多普勒计算公式和利用压缩感知重构弹道导弹微多普勒的方法。在低采样频率下利用压缩感知理论从回波信号中提取的微多普勒，与在高采样频率下利用Gabor变换提取的微多普勒是一致的，这表明利用压缩感知理论以低频率采样弹道导弹回波信号，提取微多普勒，降低工程实现难度的方法是可行的、有效的。

［1］李 谦，林昌禄.用于雷达目标识别的理想极化参数模型［J］.电波科学学报，1998，13（4）：393－397.

LI Qian，LIN Changlu.Idealized polarimetric parametric model for radar target recognition［J］.Chinese Journal of Radio Science，1998，13（4）：393－397.（in Chinese）

［2］刘永祥，黎 湘，庄钊文.导弹防御系统中的雷达目标识别技术进展［J］.系统工程与电子技术，2006，28（8）：1188－1193.

LIU Yongxiang，LI Xiang，ZHUANG Zhaowen.Review of radar target discrimination in ballistic missile defense system［J］.Systems Engineering and Electronics，2006，28（8）：1188－1193.（in Chinese）

［3］冯德军.弹道中段目标雷达识别与评估研究［D］.长沙：国防科学技术大学，2006.

［4］高红卫，谢良贵，文树梁，等.基于微多普勒特征的真假目标雷达识别研究［J］.电波科学学报，2008，23（4）：775－780.

GAO Hongwei，XIE Lianggui，WEN Shuyong，et al.Research on radar target identification of warhead and decoys based on micro－Doppler signature［J］.Chinese Journal of Radio Science，2008，23（4）：775－780.（in Chinese）

［5］CHEN V C，LI F Y，HOL S－S.Micro－Doppler effect in radar：Phenomenon，model and simulation study［J］.IEEE Trans.on AES，2006，42（1）：2－21.

［6］孙慧霞，刘 铮，薛 宁.自旋进动目标的微多普勒特征分析［J］.系统工程与电子技术，2009，31（2）：357－360.

SUN Huixia，LIU Zheng，XUE Ning.Micro－Doppler analysis of spinning－precession targets［J］.Systems Engineering and Electronics，2009，31（2）：357－360.（in Chinese）

［7］孙照强，李宝柱，鲁耀兵.弹道中段进动目标的微多普勒研究［J］.系统工程与电子技术，2009，31（3）：538－561.

SUN Zhaoqiang，LI Baozhu，LU Yaobing.Research on micro－Doppler of ballistic midcourse target with precession［J］.Systems Engineering and Electronics，2009，31（3）：538－561.（in Chinese）

［8］高红卫，谢良贵，文树梁，等.弹道导弹目标微动特性的微多普勒分析与仿真研究［J］.系统仿真学报2009，21（4）：954－957＋961.

GAO Hongwei，XIE Lianggui，WEN Shuyong，et al.Micro－Doppler analysis and simulation study of micromotion performance of ballistic missile targets［J］.Journal of System Simulation，2009，21（4）：954－957＋961.（in Chinese）

［9］王 涛，周 颖，王雪松，等.雷达目标的章动特性与章动频率估计［J］.自然科学进展，2006，16（3）：344－350.

WANG Tao，ZHOU Ying，WANG Xuesong，et al.Precession property and precession frequency extraction of radar targets［J］.Progress in Natural Scinence，2006，16（3）：344－350.（in Chinese）

［10］高红卫，谢良贵，文树梁，等.微多普勒的一些工程问题研究［J］系统工程与电子技术，2008，30（11）：2035－2039.

GAO Hongwei，XIE Lianggui，WEN Shuyong，et al.Research on several engineering problems of micro－Doppler［J］.Systems Engineering and Electronics，2008，30（11）：2035－2039.（in Chinese）

［11］DONOHO D L.Compressed sensing［J］.IEEE Trans.on Information Theory，2006，52（4）：1289－1306.

［12］DONOHO D L.Extensions of compressed sensing［J］.Singal Processing，2006，86（3）：533－548.

［13］TELLO M，L？PEZ－DEKKER P，MALLORQUI J J.A novel strategy for radar imaging based on compressive sensing［C］／／IGARSS 2008：213－216.

［14］MUJDAT C，MOSES R L.SAR Imaging from partial－aperture data with frequency－band omissions［C］／／Algorithms for synthetic Aperture Radar Imagery XII，Proceedings of SPIE，2005，5808：32－43.

［15］Lawrence Carin，LIU Dehong，LIN Wenbin，et al.Compressive sensing for multi－static scattering analysis［J］.Journal of Computational Physics，2009，228（9）：3464－3477.

［16］黄 琼，曲乐乐，吴秉横，等.压缩感知在超宽带雷达成像中的应用［J］.电波科学学报，2010，25（1）：77－80.

HUANG Qiong，QU Lele，WU Bingheng，et al.Compressive sensing for ultra－wideband radar imaging［J］.Chinese Journal of Radio Science，2010，25（1）：77－80.（in Chinese）

［17］石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，48（5）：1387－1389.

SHI Guangming，LIU Danhua，GAO Dahua，et al.Advances in theory and application of compressed sensing［J］.Acta Electronica Sinica，2009，48（5）：1387－1389.（in Chinese）