一种多基线相位解缠频域快速算法

黄海风 王青松 张永胜

（国防科学技术大学电子科学与工程学院，湖南 长沙 410073）

1.引 言

干涉合成孔径雷达（InSAR）是以不同视角下获取的两幅或多幅合成孔径雷达（SAR）复图像数据的相位信息为信息源进而得到地表三维信息和变化信息的一项技术。相位解缠是InSAR处理中尤为关键的一步，相位解缠结果的性能直接影响InSAR最终产品的质量。传统的单基线InSAR系统受干涉相位模糊和高程叠掩影响，在复杂地形区域相位解缠难度较大，从而极大地限制了单基线InSAR系统的高精度全球测绘能力。多基线InSAR系统的提出与实现则有效地提高了InSAR对复杂地形的测量精度和测量覆盖能力。多基线InSAR系统的最大优点就是可以充分利用其长短基线获取疏密不同的干涉相位条纹来提高相位解缠的性能，短基线可以保证相位解缠的可靠性，长基线可以提高测量精度。因此多基线系统更具吸引力，是未来发展的趋势［1］。

目前多基线相位解缠方法主要有：中国余数定律法、投影法以及线性组合法［2－3］、迭代法［4－5］、时域最 小 二 乘 法［6］、Kalman 滤 波 法［7－8］、最 大 似 然法［9－11］、最大后验法［12－13］、空－像域联合子空间正交投影法［14］和网络流法［15］等。其中多基线时域最小二乘法的基本思想是使相位梯度估计值与多个真实相位梯度加权和的差的平方和最小，这种方法本质是对误差进行平均，特点是十分稳健，但效率不高。本文提出一种多基线相位解缠的频域快速算法，该算法不同于时域算法，其基本思想是使相位梯度估计值的频域函数与各基线相位梯度频域函数加权和之差的平方和最小，将单基线情况［16］进行了很好地推广。论文首先介绍频域快速算法原理，其次给出算法步骤，最后通过仿真及实测数据处理对算法的有效性进行验证。

2.算法原理与效率

在InSAR成像中，由于噪声、低相干、地形等因素影响，使得干涉相位图并不连续或者说是有旋的，这就使得相位解缠结果与积分路径有关。如果相位函数ψm，n是个无旋场，则应满足

这样延扩的目的是使得延扩后的函数进行周期延扩后其边界满足无旋场条件。

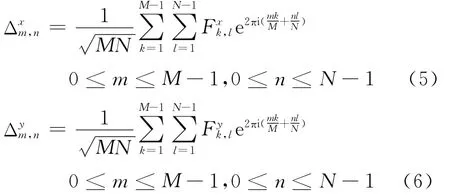
将式（5）和（6）代入满足无旋场条件的式（1）得

从而得到频域上无旋场的条件：

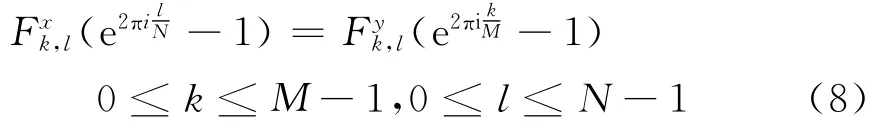
在有旋场里，式（8）并不是总成立的，但我们可以寻求和的近似值和，使得

对于单基线情况，满足

对于多基线的情况，假设共有L幅干涉图，不妨以第1幅干涉相位图为基准相位图像，设第k幅相位图与基准相位图的垂直有效基线之比为

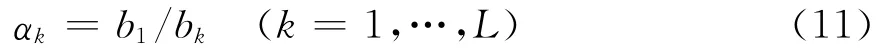
式中，bk是第k幅相位图的垂直有效基线。

设缠绕相位函数分别为（k＝1，…，L），则其相应的最小二乘解应该满足

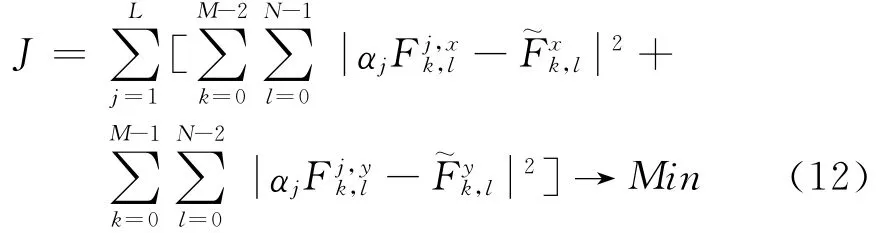
式（12）等价为

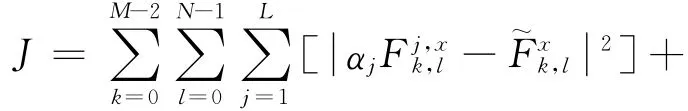
进一步有

同理有

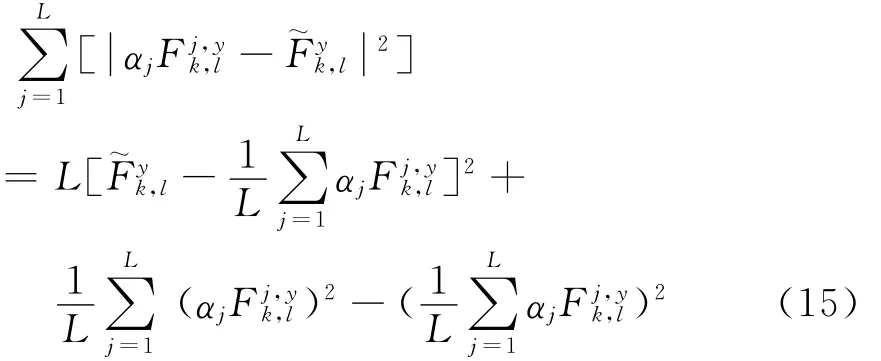
因此

式中

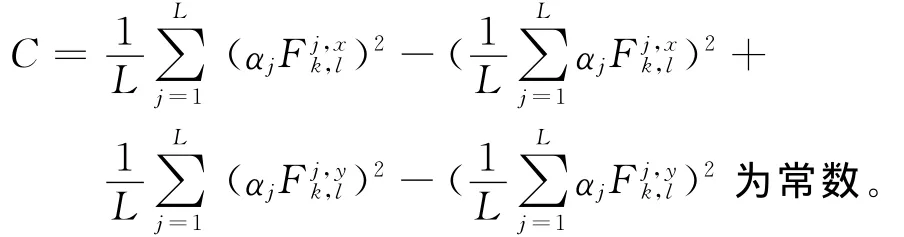
于是式（16）等价为

记C1＝ （－1），C2＝ （－1），在式（9）和式（17）的条件下可求得

式中，分别为C1和C2的共轭。上述过程的傅里叶变换总运算量为

时域方法由于要作镜像对称操作，其傅里叶变换的总运算量为

由此可见频域快速方法的运算量要小于时域方法，极大地提高了解缠效率。

3.算法步骤

在逐点计算出和后，分别对和进行FFT逆 变 换 得 到和。这 时 分 别 以和为垂直方向和水平方向的梯度的相位场便是无旋场，对其任何路径积分都得到相同的结果。这样，最后的相位恢复工作就是简单的梯度相加的过程。算法实现的具体步骤为：

步骤3：对和进行逆傅里叶变换得到和

频域最小二乘方法的精度基本上等于时域最小二乘方法，但由于该方法不用做镜像对称操作，FFT处理的数据点数小，因此可以更有效快速地得到解缠解。

4.处理性能实验验证

为了验证本文频域快速算法的有效性，利用该方法分别对仿真和实测数据进行处理。基于作者所在课题组开发的天基雷达仿真系统［17］，针对意大利的Etna火山口仿真了基线为100m、200m和300 m三种情况下干涉相位图，结果如图1所示。

图1（a）～（c）显示了基线长度分别为100m、200m和300m情况下去平地相位后的干涉相位图，图1（d）～（e）分别是时域多基线解缠结果和本文的频域多基线解缠结果。图1（f）显示了两种解缠结果相位之差。由图1（f）可知，两种解缠方法的解缠结果差异很小，但是，时域多基线解缠耗时约为13秒，频域多基线方法耗时约为4秒（干涉相位图大小：512×768像素，实验环境为Inter Core2Quad CPU 2.33GHz，内存2GB）。由此可见，本文方法在保持解缠相位精度的情况下极大地提高了解缠效率。

为了进一步验证方法的有效性，利用本文方法对伊朗Bam地区的多基线干涉数据进行处理。本研究中，三景数据为欧洲航天局ENVISAT卫星的ASAR升轨影像，影像的范围为100km×100km，其中方位向分辨率4m，距离向分辨率20m，一幅震前，两幅震后。表1显示了三景用于干涉处理的数据信息。

表1 多基线干涉数据对

震前和震后影像对配准生成干涉图后，进行了去平地相位及降噪处理。为了使得干涉图显示方便，我们采取了方位向5个像素的多视处理，最终得到分辨率为20m×20m干涉图（图幅大小：5131×4237像素），利用本文方法进行多基线相位解缠，耗时约为4分27秒，处理结果如图2所示。

图2 伊朗Bam地区不同基线情况下干涉相位及其解缠结果

5.结 论

本文研究了多基线InSAR相位解缠问题，提出了一种频域多基线相位解缠快速方法。该方法的基本思想是使相位梯度估计值的频域函数与各基线相位梯度频域函数加权和之差的平方和最小。得到无旋约束情况下的两个方向相位梯度值后，沿任意路径进行相位积分均可得到解缠结果。数据处理结果表明本文方法与时域方法的相位解缠结果差异很小，但是本文方法的运算量却小于时域方法。

致谢：此次研究所用的SAR数据由欧洲航天局（ESA）提供，精密轨道数据由荷兰Delft大学提供，在此一并表示感谢。

［1］KRIEGER G，MOREIRA A，FIEDLER H，et al.TanDEM－X：A satellite formation for high－resolution SAR interferometry［C］／／IEEE Transactions on Geoscience and Remote Sensing，2007，45：3317－3341.

［2］XU W，CHANG E C，KWOH L K，et al.Phase－unwrapping of SAR interferogram with multi－frequency or multi－baseline［C］／／Geoscience and Remote Sensing Symposium，Surface and Atmospheric Remote Sensing：Technologies，Data Analysis and Interpretation.，1994：730－732.

［3］MASSONNET D，VADON H，ROSSI M.Reduction of the need for phase unwrapping in radar interferometry［J］.IEEE Transactions on Geoscience and Remote Sensing，IGARSS＇99，1996，34（2）：489－497.

［4］ROBERTSON A E. Multi－baseline interferometric SAR for iterative height estimation［D］.Provo，UT：Brigham Young University，1998.

［5］THOMPSON D G，ROBERTSON A E，et al.Multibaseline interferometric SAR for iterative height estimation［C］／／Geoscience and Remote Sensing Symposi－um，IGARSS＇99.Hamburg ，Germany，1999：251－253.

［6］VINOGRADOV M V.Phase unwrapping method for the multifrequency and multibaseline interferometry［C］／／Geoscience and Remote Sensing Symposium Proceedings.Seattle，WA，USA，1998：1103－1105.

［7］LOFFELD O，KRAMER R.Phase unwrapping for SAR interferometry－a data fusion approach by kalman filtering［C］／／IEEE Transactions on Geoscience and Remote Sensing，2008，1：47－58.

［8］KIM M G，GRIFFITHS H D.Phase unwrapping of multibaseline interferometry using Kalman filtering［C］／／Image Processing and its Applications，Conference Publication，1999，465：813－817.

［9］LOMBARDINI F，LOMBARDO P.Maximum likelihood array SAR interferometry［C］／／IEEE Digital Signal Processing Workshop Processing.Loen，Norway，1996：358－361.

［10］LOMBARDO P，LOMBARDINI F .Multi－baseline SAR interferometry for terrain slope adaptivity［C］／／Digital Signal Processing Workshop Proceedings.Syracuse，NY，USA 1997：196－201.

［11］PASCAZIO V，SCHIRINZI G.Multifrequency In－SAR height reconstruction through maximum likelihood estimation of local planes parameters［J］.IEEE Trans.On Image Processing，2002，11（12）：1478－1489.

［12］FORNARO G，PAUCIULLO A and SANSOSTI E.Bayesian approach to phase－difference－based phase unwrapping［C］／／IEEE Thirty－sixth Asilomar Con－ference on Signals，Systems and Computers.Napoli，Italy，2002：1391－1396.

［13］POGGI G，RAGOZINI A P R，SERVADEI D.A bayesian approach for SAR interferometric phase restoration［C］／／Proc.IEEE Int.Geoscience and Remote Sensing Symp＇2000.Naples Univ.，Italy，2000：3202－3205.

［14］LI Zhenfang，BAO Zheng，LI Hai，et al.Image autocoregistration and InSAR interferogram estimation using joint subspace projection［J］.IEEE Trans.on GRS，2006，44（2）：288－297.

［15］LACHAISE M，BAMLER R.Minimum Cost Flow phase unwrapping supported by multibaseline unwrapped gradient［C］／／ Proceedings of European Conference on Synthetic Aperture Radar.Germany，2010：1－4.

［16］COSTANTINI M，FARIN A a.A fast phase unwrapping algorithm for SAR interferometry［C］／／IEEE Transactions on Geoscience and Remote Sensing，1999，37（1）：452－460.

［17］WANG Min，LIANG Diannong，YUAnxi，et al.SBRAS：An advanced simulator of spaceborne radar［C］／／Geoscience and Remote Sensing Symposium.Barcelona，2007：4942－4944.